树与图的遍历
(dfs)树与图的深度优先遍历,树的dfs序,深度与重心
深度优先遍历就是在每个点的多个分支中选择一条边走下去执行递归直到回溯到x之后 再考虑走其他的边
深度优先遍历代码如下:
静态数组邻接表:
cpp
void dfs(int x){
v[x]=1; // 记录x被访问过 也可以标记为一个时间戳
for(int i=head[x];u;u=nxt[i]){
int y=ver[i];
if(v[y])continue;
dfs(y);
}
}vector邻接表的dfs:
cpp
void dfs(int x){
v[x]=1; // 记录x被访问过 也可以标记为一个时间戳
for(auto y:edge[x]){
if(v[y])continue;
dfs(y);
}
}树的dfs序
一般来说我们在递归的时候以及回溯的时候分别记录一下节点的编号那么产生的序列就是树的dfs序 树的dfs序有以下特点 :
两个相同的序号中间部分就是以这个编号为根的树的dfs序其中包含了他的各个子树的序
代码:
cpp
void dfs(int x){
v[x]=1; // 记录x被访问过
ans[++m]=x; //记录dfs序
for(auto y:edge[x]){
if(v[y])continue;
dfs(y);
}
ans[++m]=x;
}树的深度(自顶向下)
树的深度是一种自顶向下的信息 若树的根节点的深度为0 那么他的子节点的深度为1 以此类推 子节点的深度等于父节点的深度+1 这种自顶而下的递推与dfs遍历很相似 那么我们就可以通过dfs求出每个节点的深度;
cpp
void dfs(int x){
v[x]=1; // 记录x被访问过
for(auto y:edge[x]){
if(v[y])continue;
d[y]=d[x]+1; //父节点到子节点 深度加1
dfs(y);
}
}树的重心(自底向上)
对于一棵树 我们令以x为根的树的大小为size[x] 那么对于叶子节点 他的大小就是1 若节点x 有子节点 y1~yn 那么size[x]=size[y1]+......size[yn]+1 这个信息就是自底向上的
对于一个节点x如果把他从树中删除 原来的一棵树会变为几个不相连的部分 每一部分都是一个子树 设maxpart为子树中最大的一个 那么令最大子树最小的节点就是树的重心
下面给出求重心的代码
cpp
void dfs(int x){
size[x]=1; //先只算自己 后面累加算子树
v[x]=1; // 记录x被访问过
for(auto y:edge[x]){
if(v[y])continue;
dfs(y);
size[x]+=size[y];
maxpart=max(maxpart,size[y]);
}
maxpart=max(maxpart,n-size[x]);
if(maxpart<ans){
ans=maxpart; //全局变量ans记录最大子树的最小值
pos=x; //全局变量pos记录重心
}
}图的连通块划分
每次dfs遍历 我们可以访问到相连通的所有点和边 那么我们就可以根据dfs划分连通块 对一个森林进行dfs也就能分出每个树
cpp
void dfs(int x){
v[x]=cnt; // 记录x被访问过 并且标记颜色 或者说是连通块编号
for(auto y:edge[x]){
if(v[y])continue;
dfs(y);
}
}
//主函数中进行以下代码
for(int i=1;i<=n;i++){
if(!v[i]){
cnt++;
dfs(i);
}
}(bfs)树与图的广度优先遍历 拓扑排序
树的广度优先遍历往往是通过队列实现的 每次取出队头的一个节点 然后将他的多个分支插入到队列中 然后进行下一次重复操作直到队列为空
bfs有以下特点:
1.访问完所有的第i层点后 才会开始访问i+1层点
2.队列中最多同时存在i层和i+1层 并且第i层都在第i+1层之前
也就是说bfs存在两段性和单调性
代码实现:
cpp
void bfs(){
memset(d,0,sizeof d); //每个节点的深度初始化为0;
queue<int>q;
q.push(1);v[1]=1;
d[1]=1;
while(q.size()){
int x=q.front();
q.pop();
for(auto y:edge[x]){
if(v[y])continue;
d[y]=d[x]+1;
q.push(y);
}
}
}拓扑排序
给定一张有向无环图 将图中所有的点排序 构成序列A 对于图中的有向边(x,y)如果满足a中所有的x都出现在y之前 那么这个序列就是一个拓扑序 这个排序的过程就是拓扑排序;
图的基本知识:
有向图中:
入度:有几条边能到达这个点 即以该点为终点的边个个数
出度:以该点为起点的边的个数
无向图中:
度数:无向图中以x为端点的边的个数就是度数;
对于拓扑排序 很明显类似于bfs的特点 一层一层的遍历 那么对于拓扑排序 我们只需要每次找入度为0的点 然后把连向x的点的入度减一 依次循环即可
1.建立空的拓扑序列
2.预处理所有边的入度,将入度为0的入队列;
3.取出队头x加入拓扑序
4.将x出发的所有边的入度减一 如果有被减为0的就入队列
5.重复到队列空的时候就是拓扑序;
用途: 拓扑排序可以判断一个无向图中是否存在环 如果存在环 那么拓扑序中的元素个数会小于总元素个数 而正常情况下的元素个数应该等于拓扑序中的元素个数
代码:
cpp
void topsort(){
queue<int>q;
for(int i=1;i<=n;i++){
if(deg[i]==0)q.push[i];
}
while(q.size()){
int x=q.front();
ans[++p]=x;
q.pop();
for(auto y:edge[x]){
if(--deg[y]==0)
q.push(y);
}
}
}
int main(){
cin>>n>>m; //点数 边数
for(int i=1;i<=m;i++){ //建立有向图
int u,v;
cin>>u>>v;
edge[u].push(v);
deg[v]++; //入度
}
topsort();
for(int i=1;i<=p;i++){
cout<<ans[i];
}
}P10480 可达性统计
时间限制: 1.00s 内存限制: 512.00MB
复制 Markdown 退出 IDE 模式
题目描述
给定一张 N 个点 M 条边的有向无环图,分别统计从每个点出发能够到达的点的数量。
输入格式
第一行两个整数 N,M,接下来 M 行每行两个整数 x,y,表示从 x 到 y 的一条有向边。
输出格式
输出共 N 行,表示每个点能够到达的点的数量。
输入输出样例
输入 #1复制运行
10 10
3 8
2 3
2 5
5 9
5 9
2 3
3 9
4 8
2 10
4 9输出 #1复制运行
1
6
3
3
2
1
1
1
1
1说明/提示
测试数据满足 1≤N,M≤30000,1≤x,y≤N。
cpp
#include <bits/stdc++.h>
using namespace std;
int n,m;
const int N=3e4+5;
int deg[N],ans[N],p;
bitset<30010> f[30010];
vector<int>edge[N];
void topsort(){
queue<int>q;
for(int i=1;i<=n;i++){
if(deg[i]==0)q.push(i);
}
while(q.size()){
int x=q.front();
ans[++p]=x;
q.pop();
for(auto y:edge[x]){
if(--deg[y]==0)
q.push(y);
}
}
}
void calc(){
for(int i=p;i>=1;i--){
int x=ans[i];//倒序进行 同一条链上 后面能到达的 前面也一定能到达
f[x][x]=1;
for(auto v:edge[x]){
f[x]|=f[v]; //按位或合并集合
}
}
}
int main(){
cin>>n>>m; //点数 边数
for(int i=1;i<=m;i++){ //建立有向图
int u,v;
cin>>u>>v;
edge[u].push_back(v);
deg[v]++; //入度
}
topsort();
calc();
for(int i=1;i<=n;i++){
cout<<f[i].count()<<'\n';
}
}dfs
P10483 小猫爬山
时间限制: 1.00s 内存限制: 512.00MB
复制 Markdown 退出 IDE 模式
题目描述
Freda 和 rainbow 饲养了 N(N≤18) 只小猫,这天,小猫们要去爬山。经历了千辛万苦,小猫们终于爬上了山顶,但是疲倦的它们再也不想徒步走下山了
Freda 和 rainbow 只好花钱让它们坐索道下山。索道上的缆车最大承重量为 W,而 N 只小猫的重量分别是 C1,C2,...CN。当然,每辆缆车上的小猫的重量之和不能超过 W(1≤Ci,W≤108)。每租用一辆缆车,Freda 和 rainbow 就要付 1 美元,所以他们想知道,最少需要付多少美元才能把这 N 只小猫都运送下山?
输入格式
第一行包含两个用空格隔开的整数,N 和 W。 接下来 N 行每行一个整数,其中第 i+1 行的整数表示第 i 只小猫的重量 Ci。
输出格式
输出一个整数,最少需要多少美元,也就是最少需要多少辆缆车。
输入输出样例
输入 #1复制运行
5 1996
1
2
1994
12
29输出 #1复制运行
2dfs练手题
对于每只小猫 枚举以下分支:
1.目前已经有的所有车如果放的下就放 然后dfs(now+1,cnt)
2.自己新开一个车
对于这个搜索树我们可以先进行大的猫的递归 这样的话剩下的猫想要加入车的可能性小 搜索树的分支比较小 可以加快效率;
cpp
#include <bits/stdc++.h>
using namespace std;
int n,w;
int a[20],cnt,ans,cab[20];
void dfs(int now, int cnt){
if(cnt>=ans)return;
if(now==n+1){
ans=min(ans,cnt);
return ;
}
for(int i=1;i<=cnt;i++){
if(cab[i]+a[now]<=w){
cab[i]+=a[now];
dfs(now+1,cnt);
cab[i]-=a[now]; //还原现场
}
}
cab[cnt+1]=a[now];
dfs(now+1,cnt+1);
cab[cnt+1]=0; //还原现场
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n>>w;
for(int i=1;i<=n;i++)cin>>a[i];
sort(a+1,a+1+n);reverse(a+1,a+1+n);
ans=n;
dfs(1,0);
cout<<ans;
return 0;
}剪枝
剪枝就是减少搜索树的规模,尽早排除不必要的分支的手段 在深搜中通常有以下几种
1.优化搜索顺序
在一些搜索问题中,搜索树的各个层次 分支之间的顺序不同 产生的搜索树的形态和大小也不同 因此选择合理的搜索顺序可以优化搜索树的规模 比如小猫爬山的问题中先选大的 那么后面的猫能够和这只猫放在一个车里的可能最小 分支最少 效率最高
2.排除等效冗余
搜索过程中如果几条分支是等效的 那么就只需要执行一条分支 避免遍历同一个状态空间的等效搜索树
3.可行性剪枝
搜索的过程中对当前状态进行检查 如果当前分支已经无法到达递归的边界 那就执行回溯 也叫做上下界剪枝
4.最优性剪枝
在搜索过程中如果当前代价已经超过了已经搜索到的最优解 那就回溯 因为他不可能是最优答案
5.记忆化
记录每个状态的搜索结果 在重复遍历每个状态的时候直接调用 不过不是所有的题目都要记忆化 暴搜的时候每个状态都不一样是不需要记忆化的;
下面是几道例题
P10481 Sudoku
时间限制: 2.00s 内存限制: 512.00MB
复制 Markdown
中文
退出 IDE 模式
题目描述
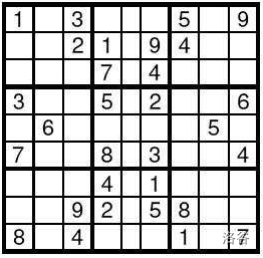
数独是一个非常简单的任务。一个包含 9 行和 9 列的正方形表格被分成了 9 个小的 3x3 方块,如图所示。一些单元格中写有从 1 到 9 的十进制数字。其他单元格为空。目标是以从 1 到 9 的十进制数字填充空单元格,每个单元格一个数字,使得每行、每列和每个标记的 3x3 子方块中都出现从 1 到 9 的所有数字。编写一个程序来解决给定的数独任务。
输入格式
输入数据将以测试用例的数量开始。对于每个测试用例,将跟随 9 行,对应于表格的行。在每一行上,给出一个正好包含 9 个十进制数字的字符串,对应于该行中的单元格。如果一个单元格为空,则用 0 表示。
输出格式
对于每个测试用例,你的程序应该以与输入数据相同的格式打印解决方案。空单元格必须按照规则填充。如果解不唯一,则程序可以打印其中任何一个。
翻译来自于:ChatGPT
显示翻译
题意翻译
输入输出样例
输入 #1复制运行
1
103000509
002109400
000704000
300502006
060000050
700803004
000401000
009205800
804000107输出 #1复制运行
143628579
572139468
986754231
391542786
468917352
725863914
237481695
619275843
854396127附件下载
validator.cpp1.94KB
对于这道题 我们每次可以选择一个空位 枚举他所有的可行的选择 然后递归进行下一个空位 重复操作 直到合法 但是这种暴力搜索的时间复杂度过高 需要进行优化和剪枝
我们要对每一行每一列每一个九宫格都记录可以用的数字 这个过程可以用数组实现 也可以用多个不同的二进制数字来实现 通过lowbit运算我们可以取出能填的数字
那么对于这道题 我们要优化搜索顺序 每次优先选择可行的选择最小的格子 使得搜索树的分支和规模最小
cpp
#include <bits/stdc++.h>
using namespace std;
int row[9],line[9],grid[9],cnt[513],num[513],tot;
char str[10][10];
int n;
int getgird(int x,int y){
return (x/3*3)+y/3;
}
void flip(int x,int y,int z){
row[x]^=1<<z;
line[y]^=1<<z;
grid[getgird(x,y)]^=1<<z;
}
bool dfs(int now){
if(now==0)return 1;
int temp=10,x=-1,y=-1;
for(int i=0;i<9;i++){
for(int j=0;j<9;j++){
if (str[i][j] != '0') continue;
int val=row[i]&line[j]&grid[getgird(i,j)];
if(val==0)return 0;
if(cnt[val]<temp){
temp=cnt[val];
x=i,y=j;
}
}
}
if(x==-1||y==-1)return 0;
int val = row[x] & line[y] & grid[getgird(x, y)];
for(;val;val-=val&-val){
int z=num[val&-val]; //映射对应的位
str[x][y]='1'+z;
flip(x,y,z);
if(dfs(now-1))return 1;
flip(x,y,z);
str[x][y]='0';
}
return 0;
}
void solve(){
tot=0;
for (int i = 0; i < 9; i++) {
row[i] = line[i] = grid[i] = (1 << 9) - 1;
}
for(int i=0;i<9;i++)
for(int j=0;j<9;j++){
cin>>str[i][j];
if(str[i][j]!='0'){
flip(i,j,str[i][j]-'1');
}
else tot++;
}
dfs(tot);
for(int i=0;i<9;i++){
for(int j=0;j<9;j++){
cout<<str[i][j];
}
cout<<'\n';
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
cin>>t;
for(int i=0;i<=(1<<9);i++){
cnt[i]=0;
for(int j=i;j;j-=j&-j)cnt[i]++;
}
for(int i=0;i<9;i++){
num[1<<i]=i;
}
while(t--){
solve();
}
return 0;
}P1120 小木棍
时间限制: 260ms 内存限制: 128.00MB
复制 Markdown
中文
退出 IDE 模式
题目背景
本题不保证 存在可以通过满足本题数据范围的任意数据做法。可以通过此题的程序不一定完全正确(算法时间复杂度错误、或不保证正确性)
本题为搜索题,本题不接受 hack 数据。关于此类题目的详细内容
题目描述
乔治有一些同样长的小木棍,他把这些木棍随意砍成几段,直到每段的长都不超过 50。
现在,他想把小木棍拼接成原来的样子,但是却忘记了自己开始时有多少根木棍和它们的长度。
给出每段小木棍的长度,编程帮他找出原始木棍的最小可能长度。
输入格式
第一行是一个整数 n,表示小木棍的个数。
第二行有 n 个整数,表示各个木棍的长度 ai。
输出格式
输出一行一个整数表示答案。
输入输出样例
输入 #1复制运行
9
5 2 1 5 2 1 5 2 1输出 #1复制运行
6说明/提示
对于全部测试点,1≤n≤65,1≤ai≤50。
搜索题 但是需要进行优化和剪枝才能通过 首先我们要枚举每条原始木棍的长度 由于最终的答案是原始木棍最小的答案 那么我们就从最小值也就是切完中的木棍中最大的开始枚举 对于合法的长度 进行dfs dfs的时候 如果总共的拼好的数量比总数大 那就return true 如果当前长度等于len 返回dfs(num+1,0,1) 也就是拼下一根 看能不能拼好
我们拼木棍的时候优先拼大的 再拼小的可以减少分支 减小搜索树的规模 增加效率 然后加上标记数据 防止重复利用 由于相邻木棍可能相同 如果相同长度的第一根木棍不行 那么后面的都不行 添加一个标记 fall 表示上一个失败的元素 来跳过重复的元素 拼接的时候如果拼接后的dfs返回true 也就是后面可以拼好 那么就返回true 如果没品好 可能有几种情况 一种是cab=0 说明有一种棍子大于len 所有的都不兼容 如果cab+a[i]==len 也就是完美兼容的情况下 后续部分拼不好 那么说明整个部分都拼不好了 那么就返回false;
cpp
#include <bits/stdc++.h>
using namespace std;
int n;
const int N=1e2+5;
int a[N],v[N];
int cnt=0,len;
bool dfs(int num,int cab,int last){
if(num>cnt)return true;
if(cab==len)return dfs(num+1,0,1);
int fall=0;
for(int i=last;i<=n;i++){
if(!v[i]&&cab+a[i]<=len&&fall!=a[i]){
v[i]=1;
if(dfs(num,cab+a[i],i+1))return true;
fall=a[i];
v[i]=0;
if(cab==0||cab+a[i]==len)return false;
}
}
return false;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n;
int maxn=0;
int sum=0;
for(int i=1;i<=n;i++){
cin>>a[i];
sum+=a[i];
if(a[i]>maxn)maxn=a[i];
}
sort(a+1,a+1+n);reverse(a+1,a+1+n);
for(len=maxn;len<=sum;len++){
if(sum%len)continue;
cnt=sum/len;
memset(v,0,sizeof v);
if(dfs(1,0,1))break;
}
cout<<len;
return 0;
}P1731 [NOI1999] 生日蛋糕
时间限制: 1.00s 内存限制: 512.00MB
复制 Markdown
中文
退出 IDE 模式
题目背景
题目描述
7 月 17 日是 Mr.W 的生日,ACM-THU 为此要制作一个体积为 Nπ 的 M 层生日蛋糕,每层都是一个圆柱体。
设从下往上数第 i(1≤i≤M)层蛋糕是半径为 Ri,高度为 Hi 的圆柱。当 i<M 时,要求 Ri>Ri+1 且 Hi>Hi+1。
由于要在蛋糕上抹奶油,为尽可能节约经费,我们希望蛋糕外表面(最下一层的下底面除外)的面积 Q 最小。
请编程对给出的 N 和 M,找出蛋糕的制作方案(适当的 Ri 和 Hi 的值),使 S=πQ 最小。
(除 Q 外,以上所有数据皆为正整数)
输入格式
第一行为一个整数 N(N≤2×104),表示待制作的蛋糕的体积为 Nπ。
第二行为 M(M≤15),表示蛋糕的层数为 M。
输出格式
输出一个整数 S,若无解,输出 0。
输入输出样例
输入 #1复制运行
100
2输出 #1复制运行
68对于这道题 我们要保证体积一定的情况下 表面积最小 每层蛋糕的上表面的面积之和 等于最下面一层的底面积 那么表面积也就是底面积加上每一层的侧面积 由于题目中加了PAI 所以我们可以去掉pai
v=PAI *r*r*h;
侧面积等于2*PAI*r*h;
从下到上 r h 递减
搜索顺序 从下往上 因为总空间一定 所以从大到小搜索可以减少分支 减小搜索树规模
同理每一层也都是从大到小枚举
1.上下界剪枝 由于半径和高度都严格递减 如果我们定义最上面为第一层 最小面为最后一层 记录已经搜索的体积为v 那么有
第dep层的时候 r的范围为[dep,min(sqrt(N-v),dep[r+1]-1) 也就是说 半径的最小值等于层数 最大值为体积限制下的最大半径和 满足半径递减的最小值
第dep层的时候 h的范围为[dep,min((N-v)/R^2,h[dep+1]-1)];
2.优化搜索顺序
从下到上搜索可以使得当前v最大 使得体积限制更多 决策数更少 减少搜索树的规模;
3.可行性剪枝
预处理出从上往下前M层面积和体积的最小值 也就是让r h尽可能取最小值 如果当前层加上上面几层的最小值的体积仍然大于N 那么就剪枝
4.最优性剪枝
如果当前侧面积加上上面几层的最小侧面积已经大于最优解了 那么也剪枝
5.最优性剪枝
不等式剪枝 根据不同维度之间的数量关系 构建一个不等式 最优性剪枝
总结思路 代码流程: 输入数据 预处理最小值面积 体积 然后递归 递归的时候 如果剩余层数小于0 那么检查体积是否为N 是的话更新答案 然后结束递归 枚举半径 高 从大到小 剪枝 计算加上最小面积和体积是否合理 不合理直接进行下一次枚举 不等式剪枝 面积体积累加 如果是最底层 记得加上底面积 进行下一层的递归 还原现场 最后输出答案
代码实现
cpp
#include <bits/stdc++.h>
using namespace std;
const int N=30;
int ans=INT_MAX;
int r[N],h[N],mins[N],minv[N],s,v;
int n,m;
void dfs(int dep){
if(dep<=0){
if(v==n)ans=min(ans,s);
return ;
}
for(r[dep]=min((int)sqrt(n-v),r[dep+1]-1);r[dep]>=dep;r[dep]--)
for(h[dep]=min((int)((double)(n-v)/(r[dep]*r[dep])),h[dep+1]-1);h[dep]>=dep;h[dep]--){
if(v+minv[dep-1]>n)continue;
if(s+mins[dep-1]>ans)continue;
if (s + (double)2 * (n - v) / r[dep] > ans) continue;
if(dep==m)s+=r[dep]*r[dep];
s+=2*r[dep]*h[dep];
v+=r[dep]*r[dep]*h[dep];
dfs(dep-1);
if(dep==m)s-=r[dep]*r[dep];
s-=2*r[dep]*h[dep];
v-=r[dep]*r[dep]*h[dep];
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>n>>m;
r[m+1]=h[m+1]=INT_MAX;
for(int i=1;i<=m;i++){
minv[i]=minv[i-1]+i*i*i;
mins[i]=mins[i-1]+2*i*i;
}
dfs(m);
if(ans==INT_MAX)ans=0;
cout<<ans;
return 0;
}迭代加深
当搜索树的规模增长特别快 而答案确定在一个较浅的节点上 那么可以采用迭代加深DFS 控制搜索的深度 避免在不必要的分支浪费搜索时间
UVA529 Addition Chains
时间限制: 3.00s 内存限制: 0B
复制 Markdown
中文
退出 IDE 模式
题目描述
一个与 n 有关的整数加成序列 <a0,a1,a2,...,am> 满足以下四个条件:
1.a0=1
2.am=n
3.a0<a1<a2<...<am−1<am
- 对于每一个 k(1≤k≤m) 都存在有两个整数 i 和 j(0≤i,j≤k−1,i 和 j 可以相等 ) ,使得 ak=ai+aj
你的任务是:给定一个整数 n ,找出符合上述四个条件的长度最小的整数加成序列。如果有多个满足要求的答案,只需要输出任意一个解即可。
举个例子,序列 <1,2,3,5> 和 <1,2,4,5> 均为 n=5 时的解。
输入格式
输入包含多组数据。每组数据仅一行包含一个整数 n(1≤n≤10000) 。在最后一组数据之后是一个 0 。
输出格式
对于每组数据,输出一行所求的整数加成序列,每个整数之间以空格隔开。
感谢@Iowa_BattleShip 提供的翻译
显示翻译
题意翻译
输入输出样例
输入 #1复制运行
5
7
12
15
77
0输出 #1复制运行
1 2 4 5
1 2 4 6 7
1 2 4 8 12
1 2 4 5 10 15
1 2 4 8 9 17 34 68 77对于每一个位置k 我们都可以枚举比它小的i 和j 将他们的位置的和填写到k位置上 然后递归下一个位置
为了使得序列尽可能短 加入以下剪枝
1.挑选i j 的时候 从大到小 尽快的逼近n避免无效搜索
2.标记数组 标记已经尝试但是失败了的和 避免无效重复
cpp
#include <bits/stdc++.h>
using namespace std;
const int N=106;
int ans[N],dep;
int n;
bool v[5*N];
bool dfs(int now){
if(now==dep)return ans[now]==n;
memset(v,false,sizeof v);
for(int i=now;i>=1;i--)
for(int j=i;j>=1;j--){
int num=ans[i]+ans[j];
if(num<=n&&num>ans[now]&&!v[num]){
ans[now+1]=num;
if(dfs(now+1))return 1;
v[num]=1;
}
}
return 0;
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
while(cin>>n&&n){
ans[1]=1;
dep=1;
while(!dfs(1))++dep;
for(int i=1;i<=dep;i++)cout<<ans[i]<<' ';
cout<<'\n';
}
return 0;
}双向搜索
当题目的初态和终态都确定 并且从初态搜索和从终态逆向搜索 都可以覆盖整个搜索树 那么可以采用双向搜索的办法 产生两颗规模较小的子树 避免搜索树的规模过大
P10484 送礼物
时间限制: 2.00s 内存限制: 512.00MB
复制 Markdown 退出 IDE 模式
题目描述
作为惩罚,GY 被遣送去帮助某神牛给女生送礼物 (GY:貌似是个好差事)但是在 GY 看到礼物之后,他就不这么认为了。某神牛有 N 个礼物,且异常沉重,但是 GY 的力气也异常的大 (-_-b),他一次可以搬动重量和在 w 以下的任意多个物品。GY 希望一次搬掉尽量重的一些物品,请你告诉他在他的力气范围内一次性能搬动的最大重量是多少。
输入格式
第一行两个整数,分别代表 W 和 N。
以后 N 行,每行一个正整数表示 Gi。
输出格式
仅一个整数,表示 GY 在他的力气范围内一次性能搬动的最大重量。
输入输出样例
输入 #1复制运行
20 5
7
5
4
18
1输出 #1复制运行
19说明/提示
对于所有测试数据,1≤N≤46, 1≤W,G[i]≤231−1。
子集和问题 选择一个子集 使得他的和尽可能接近w每个数字都有选和不选两种 也就是指数级枚举 这样复杂度过高 我们可以双线搜索解决
排序后挑出一半 将所有的和的合法的可能的情况存储起来 排序后去重
枚举另一半的所有和的可能为t 然后二分查找上一半搜索的所有答案 中 不超过w-t的最大值 然后比较答案 更新答案;
对于这个过程 一半一半可能并不是最优的分配 实际上 前一半部分多分一部分 效率会成高
cpp
#include <bits/stdc++.h>
using namespace std;
unsigned int g[50];
vector<unsigned int >a;
unsigned int w,n,ans;
void dfs1(int k,unsigned x){
if(k==0){
a.push_back(x);
return ;
}
dfs1(k-1,x);
if(x+g[k]<=w)dfs1(k-1,x+g[k]);
}
void dfs2(int k,unsigned int x){
if(k==n+1){
int y=*--upper_bound(a.begin(),a.end(),w-x);
ans=max(ans,x+y);
return ;
}
dfs2(k+1,x);
if(x+g[k]<=w)dfs2(k+1,x+g[k]);
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin>>w>>n;
for(int i=1;i<=n;i++)cin>>g[i];
sort(g+1,g+1+n);
reverse(g+1,g+1+n);
dfs1(n/2+1,0);
sort(a.begin(),a.end());
unique(a.begin(),a.end());
dfs2(n/2+2,0);
cout<<ans;
return 0;
}BFS
P10485 Bloxorz I
时间限制: 1.00s 内存限制: 512.00MB
复制 Markdown
中文
退出 IDE 模式
题目背景
小汤姆喜欢玩游戏。有一天,他下载了一个叫做"Bloxorz"的小电脑游戏,让他非常兴奋。
题目描述
这是一个关于将一个方块滚动到特定位置的游戏。准确地说,这个平面由几个单位单元格组成,是一个矩形形状的区域。而方块由两个完美对齐的单位立方体组成,可以躺下并占据两个相邻的单元格,也可以站立并占据一个单独的单元格。
你可以通过选择方块在地面上的四条边之一,并围绕该边旋转 90 度来移动方块,每次旋转算作一步。有三种类型的单元格,刚性单元格、易碎单元格和空单元格。
- 刚性单元格可以支撑方块的全部重量,因此可以是方块所占据的两个单元格中的任意一个,也可以是方块完全站立在上面的单元格。
- 易碎单元格只能支撑方块重量的一半,因此不能是方块完全站立在上面的唯一单元格。
- 空单元格无法支撑任何东西,因此方块不可能部分位于该单元格上。
游戏的目标是以最少的步数将站立的方块滚动到平面上唯一的目标单元格。

方块站在单个单元格上。

方块横躺在两个相邻的单元格上。

方块纵躺在两个相邻的单元格上。
在小汤姆通过游戏的几个阶段后,他发现比他预期的要难得多。因此,他求助于你的帮助。
输入格式
输入包含多个测试案例。
每个测试案例都是游戏的一个阶段。它以两个整数 R 和 C 开头,表示平面的行数和列数。
接下来是平面,其中包含 R 行和每行的 C 个字符,其中 O 表示目标单元格,X 表示方块的初始位置,. 表示刚性单元格,# 表示空单元格,E 表示易碎单元格。一个测试案例以两个 0 结束输入。
输入保证:
- 平面上只有一个
O。 - 平面上要么有一个
X,要么有相邻的两个X。 - 第一行(和最后一行)(以及第一列和最后一列)必须是
#(空单元格)。 O和X覆盖的单元格都是刚性单元格。
输出格式
对于每个测试案例,输出一行表示移动的最小次数,或在无法达到目标单元格时输出 Impossible。
显示翻译
题意翻译
输入输出样例
输入 #1复制运行
7 7
#######
#..X###
#..##O#
#....E#
#....E#
#.....#
#######
0 0输出 #1复制运行
10说明/提示
数据范围
对于所有的数据:3≤R,C≤500。
翻译
翻译来自于:ChatGPT。
cpp
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
struct rec { int x, y, lie; }; // 状态
char s[510][510]; // 地图
rec st, ed; // 起始状态和目标状态
int n, m, d[510][510][3]; // 最少步数记录数组
queue<rec> q; // 队列
bool valid(int x, int y) { return x>=1 && y>=1 && x<=n && y<=m; }
// 方向数组(方向0~3依次代表左右上下)
const int dx[4] = { 0,0,-1,1 }, dy[4] = { -1,1,0,0 };
void parse_st_ed() { // 处理起点和终点
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
if (s[i][j] == 'O') { //终点
ed.x = i, ed.y = j, ed.lie = 0, s[i][j] = '.'; //状态 坐标 刚性快
}
else if (s[i][j] == 'X') { //起点
for (int k = 0; k < 4; k++) { //枚举四个方位 判断是否有相邻的两个x
int x = i + dx[k], y = j + dy[k];
if (valid(x, y) && s[x][y] == 'X') { //范围合法 且为x
st.x = min(i,x), st.y = min(j,y), st.lie = k<2?1:2;
s[i][j] = s[x][y] = '.';
break;
}
}
if (s[i][j] == 'X') {
st.x = i, st.y = j, st.lie = 0;
}
}
}
bool valid(rec next) { // 滚动是否合法
if (!valid(next.x, next.y)) return 0;
if (s[next.x][next.y] == '#') return 0;
if (next.lie == 0 && s[next.x][next.y] != '.') return 0;
if (next.lie == 1 && s[next.x][next.y + 1] == '#') return 0;
if (next.lie == 2 && s[next.x + 1][next.y] == '#') return 0;
return 1;
}
// next_x[i][j]表示在lie=i时朝方向j滚动后x的变化情况
const int next_x[3][4] = { { 0,0,-2,1 },{ 0,0,-1,1 },{ 0,0,-1,2 } };
// next_y[i][j]表示在lie=i时朝方向j滚动后y的变化情况
const int next_y[3][4] = { { -2,1,0,0 },{ -1,2,0,0 },{ -1,1,0,0 } };
// next_lie[i][j]表示在lie=i时朝方向j滚动后lie的新值
const int next_lie[3][4] = { { 1,1,2,2 },{ 0,0,1,1 },{ 2,2,0,0 } };
int bfs() { // 广搜
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
for (int k = 0; k < 3; k++) d[i][j][k] = -1; //重置初始化为-1
while (q.size()) q.pop(); //重置初始化
d[st.x][st.y][st.lie] = 0; //起点步数为0
q.push(st);
while (q.size()) {
rec now = q.front(); q.pop(); // 取出队头
for (int i = 0; i < 4; i++) { // 向4个方向滚动
rec next;
next.x = now.x + next_x[now.lie][i];
next.y = now.y + next_y[now.lie][i];
next.lie = next_lie[now.lie][i];
if (!valid(next)) continue; //不合法
if (d[next.x][next.y][next.lie] == -1) { // 尚未访问过
d[next.x][next.y][next.lie] = d[now.x][now.y][now.lie]+1; //步数传递累加1
q.push(next);
if (next.x == ed.x && next.y == ed.y && next.lie == ed.lie)
return d[next.x][next.y][next.lie]; // 到达目标
}
}
}
return -1; // 无解
}
int main() {
while (cin >> n >> m && n) {
for (int i = 1; i <= n; i++) scanf("%s", s[i] + 1);
parse_st_ed();
int ans = bfs();
if (ans == -1) puts("Impossible"); else cout << ans << endl;
}
}