汽车FMCW雷达互扰下的快速目标检测:谱峰累积法与泊松CFAR精读与推导
A. Mingshun, Y. Weijie, X. Li, Y. Guang, Y. Lingling and Y. Zijiang, "Fast Algorithm for Automotive Radar Target Detection in Mutual Interference," in IEICE Communications Express, vol. 13, no. 2, pp. 26-29, February 2024, doi: 10.23919/comex.2023XBL0118.
1. 研究问题与核心思路
文中聚焦于车载FMCW毫米波雷达的互扰(mutual interference) :当道路车辆密集、多个雷达处于同频段工作时,受害雷达(victim radar)接收端会混入来自另一台雷达的强外部信号。该外部信号在去斜(dechirp)后往往呈现为扫频型中频干扰,会显著抬升IF频谱底噪,从而使传统基于幅度统计的检测(例如常规CA-CFAR)性能急剧下降。
文中提出的"谱峰累积法 "(spectral peak accumulation method, SPAM)刻意绕开"先抑制干扰/重构信号,再检测"的常规路径,而是利用一个更"结构化"的判别线索:
在时频域 里,目标回波与扫频互扰的能量分布形态 不同------目标回波在IF上更接近"稳定的窄带成分",而扫频互扰更像"横跨频带的非平稳轨迹/散布"。因此算法先做时频分解,再在每个时刻的频率切片中只保留"峰的位置"(忽略峰的幅度强弱),最后将这些峰的位置沿时间累积成一条与频率轴对齐的"峰计数向量"。文中指出在无目标时该向量可用泊松分布 刻画,从而构造一个泊松常虚警检测(Ps-CFAR)阈值来检出目标峰。
2. FMCW互扰信号模型:从发射、回波到去斜后的IF表达
2.1 发射信号(线性调频chirp)
文中将FMCW发射信号写为(原式(1)):
Str(t)=exp{j2π(f0t+12ut2)}(1) S_{tr}(t)=\exp\left\{j2\pi\left(f_0 t+\frac{1}{2}u t^2\right)\right\}\tag{1} Str(t)=exp{j2π(f0t+21ut2)}(1)
其中 f0f_0f0 为起始频率,uuu 为调频斜率(单位Hz/s)。
2.2 目标回波信号
目标回波建模为若干散射体叠加(原式(2)):
Secho(t)=∑i=1nai⋅Str(t−Δτ)(2) S_{echo}(t)=\sum_{i=1}^{n}a_i\cdot S_{tr}(t-\Delta\tau)\tag{2} Secho(t)=i=1∑nai⋅Str(t−Δτ)(2)
这里 aia_iai 是传播衰减因子,Δτ\Delta\tauΔτ 是回波延迟。文中未展开"Δτ\Delta\tauΔτ 与距离"的关系;在FMCW常规物理模型中,单目标距离 RRR 通常对应 Δτ=2R/c\Delta\tau=2R/cΔτ=2R/c。
2.3 外部互扰信号(另一台FMCW雷达)
干扰雷达同样发射FMCW信号(原式(3)):
SI(t)=exp{j2π[fI(t−Δt)+12uI(t−Δt)2]}(3) S_I(t)=\exp\left\{j2\pi\left[f_I(t-\Delta t)+\frac{1}{2}u_I(t-\Delta t)^2\right]\right\}\tag{3} SI(t)=exp{j2π[fI(t−Δt)+21uI(t−Δt)2]}(3)
其中 fI,uIf_I,u_IfI,uI 分别是干扰雷达的起始频率与调频斜率,Δt\Delta tΔt 是两雷达信号到达/对齐上的相对延迟。
2.4 去斜后的IF信号:回波拍频 + 互扰项
当受害雷达同时接收到目标回波与外部互扰并进行去斜,文中给出IF表示(原式(4)):
SIF=Str⋅(Secho∗+p⋅SI∗)=∑i=1naifbi(t)+p⋅Str⋅SI∗(4) S_{IF}=S_{tr}\cdot\left(S_{echo}^{*}+p\cdot S_I^{*}\right) =\sum_{i=1}^{n}a_i f_{b_i}(t)+p\cdot S_{tr}\cdot S_I^{*}\tag{4} SIF=Str⋅(Secho∗+p⋅SI∗)=i=1∑naifbi(t)+p⋅Str⋅SI∗(4)
其中 (⋅)∗(\cdot)^{*}(⋅)∗ 表示共轭,fbi(t)f_{b_i}(t)fbi(t) 表示回波拍频分量(文中表述为IF带内余弦信号),ppp 为互扰信号的传播衰减因子。由于互扰信号"直达"进入受害雷达,其强度通常远高于反射回波。
文中进一步令互扰去斜项为
SMI=p⋅Str⋅SI∗ S_{MI}=p\cdot S_{tr}\cdot S_I^{*} SMI=p⋅Str⋅SI∗
并指出当 uI≠uu_I\neq uuI=u 时,SMIS_{MI}SMI 是一个斜率为 u−uIu-u_Iu−uI 的线性调频信号("sweeping interference"),会在低通滤波器截止频率 fcutofff_{\text{cutoff}}fcutoff 内呈现扫频特征;若 uI=uu_I=uuI=u,则 SMIS_{MI}SMI 退化为余弦型"平行干扰"(parallel interference),可能引发虚假目标,但文中认为其出现概率低,工程上可忽略。
图1:FMCW雷达结构示意(发射链路、接收链路与互扰注入位置)
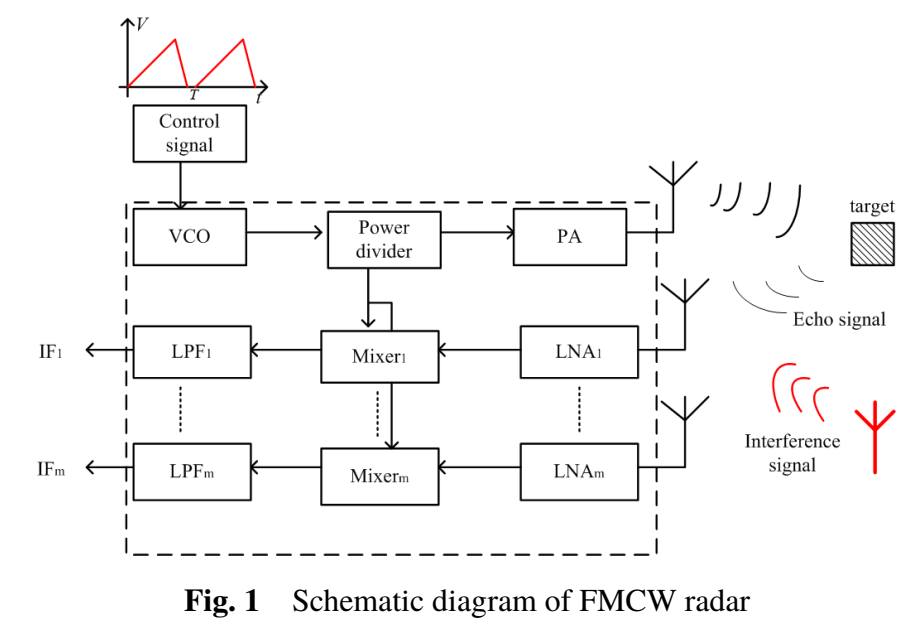
图中给出典型FMCW体制:控制信号驱动VCO产生chirp,经功放/天线发射;接收端同时接收目标回波与外部互扰信号,经LNA、混频与低通得到IF输出。该结构强调了互扰信号以"外来输入"的方式进入同一接收链路,因此在IF域对检测造成直接破坏。
图2:时频域视角下的"扫频互扰"与"平行互扰",以及对应IF表现
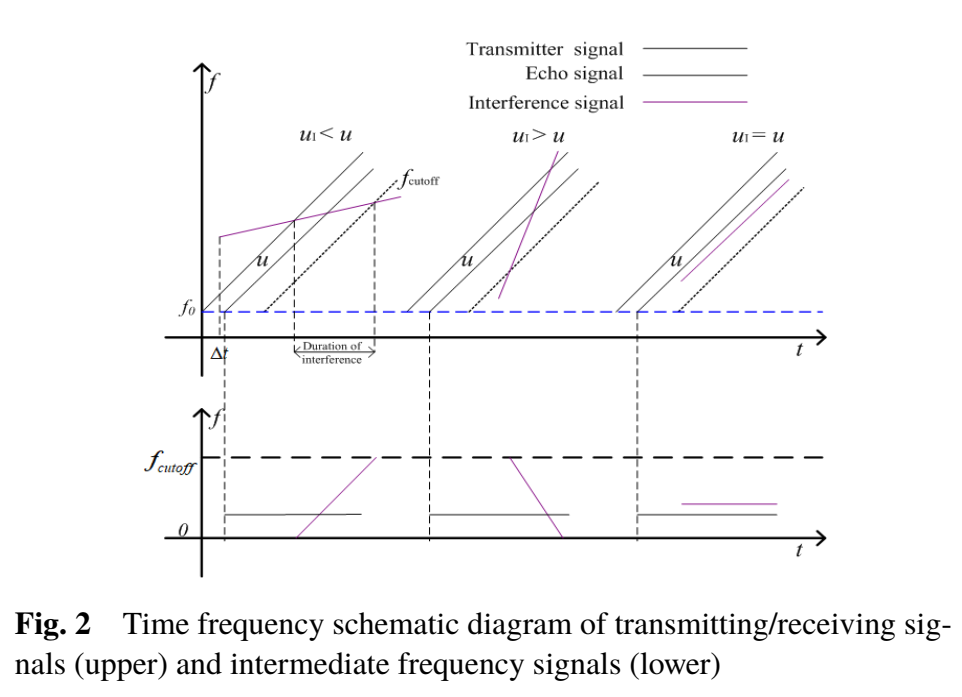
图2上半部分画出发射信号、回波与互扰信号在时频平面中的相对斜率关系;下半部分对应去斜后的IF频率随时间变化。关键点是:当 uI≠uu_I\neq uuI=u 时,互扰去斜项在IF内表现为随时间变化的扫频分量,并在低通截止频率限制下形成"进带---出带"的非平稳结构;而目标拍频更接近"在某一固定频率附近保持稳定"的成分。这一"结构差异"正是后续SPAM想利用的判据。
3. 谱峰累积法(SPAM):把"强度问题"转化为"分布问题"
SPAM的核心不是比较幅度大小,而是比较"峰在时频域中出现的位置分布"。为此,算法将问题改写为:
在时频矩阵中,每个时间切片(每一行)找出若干"谱峰位置",将其映射为0-1矩阵,再对频率列做累积,得到与频率轴对齐的计数向量 CCC。目标回波由于频率稳定,会在同一频率列上反复出现峰;扫频互扰由于频率随时间漂移,峰位置更分散,列累积更接近"随机计数"。
3.1 时频分解:Gabor变换
文中采用Gabor变换做时频分解(原式(5)):
G(τ,ω)=∫0TSIF(t)⋅gσ∗(t−τ)⋅e−jωt dt(5) G(\tau,\omega)=\int_{0}^{T} S_{IF}(t)\cdot g_{\sigma}^{*}(t-\tau)\cdot e^{-j\omega t}\,dt\tag{5} G(τ,ω)=∫0TSIF(t)⋅gσ∗(t−τ)⋅e−jωtdt(5)
其中窗函数为高斯核:
gσ(t)=exp(−t22σ2) g_{\sigma}(t)=\exp\left(-\frac{t^2}{2\sigma^2}\right) gσ(t)=exp(−2σ2t2)
参数 σ\sigmaσ 控制时域窗宽,从而决定时频分辨率折中。文中给出经验选取区间:
1.2⋅Bu≤σ≤2.4⋅Bu 1.2\cdot\frac{B}{u}\le \sigma \le 2.4\cdot\frac{B}{u} 1.2⋅uB≤σ≤2.4⋅uB
并指出系数 2.4≈22ln22.4\approx 2\sqrt{2\ln 2}2.4≈22ln2 与归一化高斯主瓣3dB宽度有关(这一点在附录会补全其严格对应关系)。
从信号解释上看,Gabor变换本质是对不同中心时刻 τ\tauτ 的局部窗口做傅里叶分析:对"拍频近似稳定"的目标回波,它在许多相邻窗口里都集中在同一 ω\omegaω 附近;对"扫频互扰",其能量峰随 τ\tauτ 发生漂移,从而在时频平面形成扩展结构。
3.2 谱峰搜索、二值化与列累积
文中先对时频矩阵取模 ∣G∣|G|∣G∣,再沿频率轴逐行找"谱峰"。谱峰判定条件在文中给成两条规则,可合并表述为:对固定时间行 mmm,某频率索引 nnn 为谱峰当且仅当
(1) ∣G[m,n]∣|G[m,n]|∣G[m,n]∣ 大于其左右相邻频点的值;且
(2) ∣G[m,n]∣|G[m,n]|∣G[m,n]∣ 大于该行的平均值。
随后将谱峰位置记为1,其他位置记为0,得到二值矩阵 G0−1G_{0-1}G0−1。最后对每一频率列做累积,得到谱峰累积向量(原式(6)):
C(n)=∑columnT0−1(∣G∣),n=1,2,...,N(6) C(n)=\sum_{\text{column}} T_{0-1}(|G|),\quad n=1,2,\dots,N\tag{6} C(n)=column∑T0−1(∣G∣),n=1,2,...,N(6)
其中 T0−1(⋅)T_{0-1}(\cdot)T0−1(⋅) 表示"仅在谱峰位置置1,其余置0"的算子,NNN 为频率单元数。
为了使该式更具可计算性,可将(6)写成标准矩阵形式:若时频矩阵离散后为 G∈CM×NG\in\mathbb{C}^{M\times N}G∈CM×N,则二值峰矩阵为
B[m,n]=T0−1(∣G[m,n]∣)∈{0,1}, B[m,n]=T_{0-1}(|G[m,n]|)\in\{0,1\}, B[m,n]=T0−1(∣G[m,n]∣)∈{0,1},
累积向量为
C[n]=∑m=1MB[m,n],n=1,...,N. C[n]=\sum_{m=1}^{M} B[m,n],\quad n=1,\dots,N. C[n]=m=1∑MB[m,n],n=1,...,N.
从直觉看,C[n]C[n]C[n] 就是"频率bin nnn 在多少个时间窗里被选中为谱峰"的计数。
这种二值化处理的关键作用是:把"互扰功率远强于回波"的问题从幅度域中剥离掉。即使互扰在幅度上淹没回波,若回波在很多时间窗里依然能形成局部峰(哪怕不高),那么其峰的"出现次数"仍可能在统计上可分离。
图3:时频谱、0-1峰矩阵与累积向量的对应关系
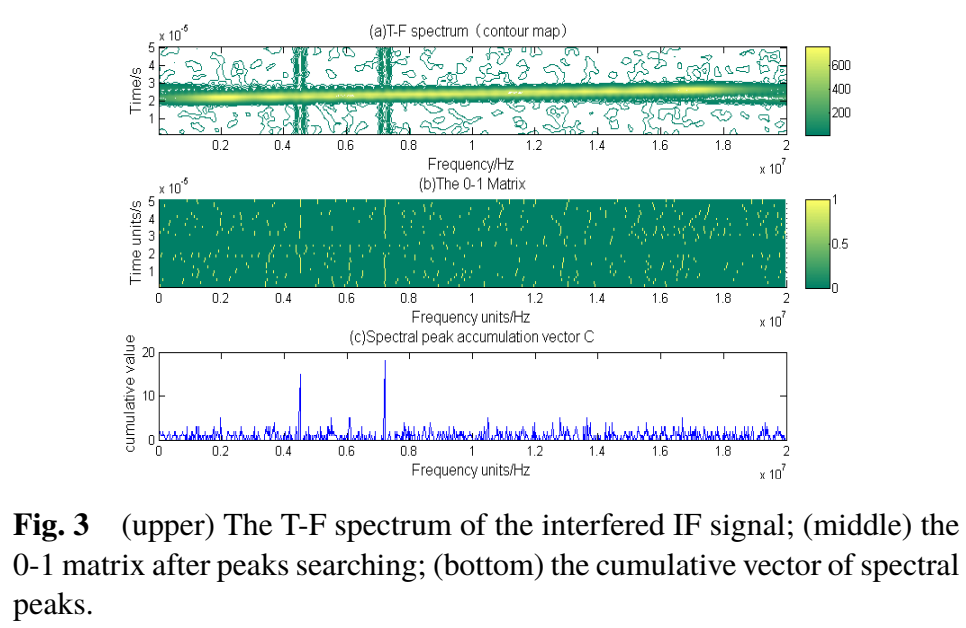
图3上部展示了干扰条件下IF信号的时频谱(亮度反映 ∣G(τ,ω)∣|G(\tau,\omega)|∣G(τ,ω)∣);中部将逐行峰检测后的峰位置二值化为0-1矩阵;下部对列累积得到 CCC。若某一目标拍频在许多时间窗里持续产生峰,则对应频率列会形成明显的"高计数尖峰"。
4. 目标检测:把累积向量建模为泊松分布,并构造Ps-CFAR阈值
4.1 从"无目标时的随机峰"到泊松模型
文中在目标检测部分指出:当IF信号中不存在目标回波 时,由噪声与互扰导致的谱峰在时频矩阵列方向上的出现可视为随机事件;按其构造方式,列累积值在严格意义上可先视作二项分布,再在一定条件下近似为泊松分布。因此 C[n]C[n]C[n] 服从泊松分布,其概率质量函数为(原式(7)):
P{x=k}=λkk!e−λ,k=0,1,2,...(7) P\{x=k\}=\frac{\lambda^{k}}{k!}e^{-\lambda},\quad k=0,1,2,\dots\tag{7} P{x=k}=k!λke−λ,k=0,1,2,...(7)
λ\lambdaλ 同时是期望与方差。文中提出一种估计方式:在"无目标环境"采集信号时,峰累积的平均值可以逼近 λ\lambdaλ。
这一步相当于给出背景统计模型:在背景下,C[n]C[n]C[n] 的大值出现概率可由泊松尾概率控制;而目标出现时,会在某个频率bin上显著抬高 C[n]C[n]C[n],从而超过阈值。
4.2 Ps-CFAR阈值:从给定虚警概率反推出门限
文中给出阈值计算关系(原式(8)):
∑k=0hλkk!e−λ=1−Pf(8) \sum_{k=0}^{h}\frac{\lambda^{k}}{k!}e^{-\lambda}=1-P_f\tag{8} k=0∑hk!λke−λ=1−Pf(8)
等价地,
P{x>h}=Pf. P\{x>h\}=P_f. P{x>h}=Pf.
这里 PfP_fPf 是设定的虚警概率(false alarm probability),hhh 是门限。该式本质是在做泊松分布的分位数求解:给定 λ\lambdaλ 与 PfP_fPf,找到最小的 hhh 使得右尾概率不超过 PfP_fPf。
文中将其类比于传统CA-CFAR:传统CA-CFAR常假设背景幅度服从瑞利分布并据此推阈值;此处则把背景模型替换为泊松分布,因此得到"Poisson CA-CFAR(Ps-CFAR)"。其检测对象不是幅度谱,而是峰计数向量 CCC。
图4:在峰累积向量上进行PsCA-CFAR检测
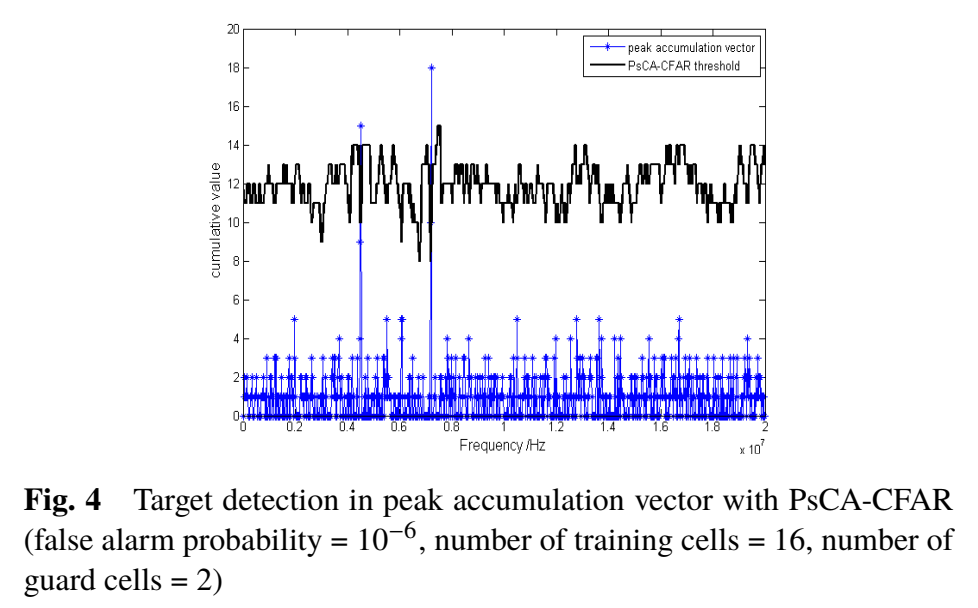
图4展示了 CCC 随频率的计数分布以及对应的CFAR门限曲线。当某频率处累积计数尖峰超过门限,即判定存在目标回波并输出该拍频位置。
5. 仿真设置与结果:在低SIR下保持高检出率
5.1 参数设置(表1)
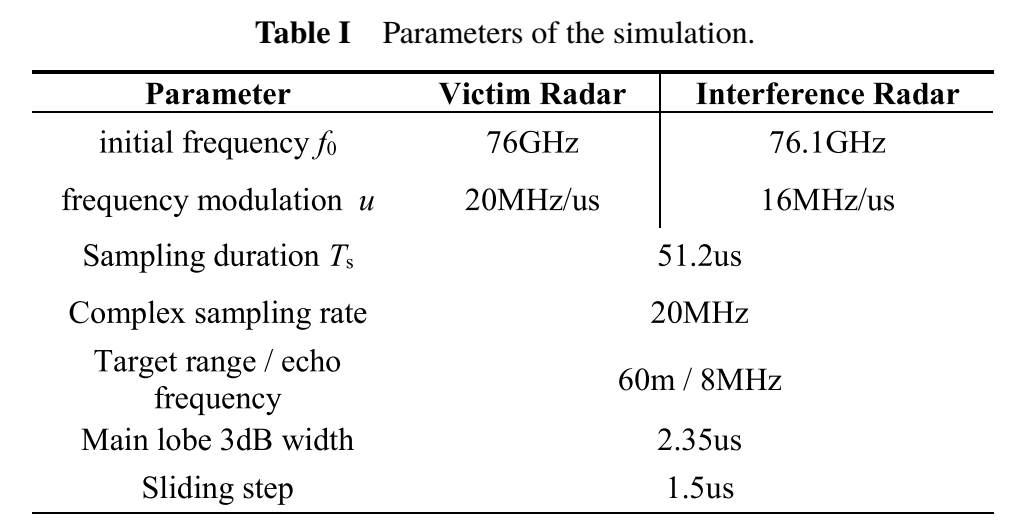
表1给出受害雷达与干扰雷达的关键参数:
受害雷达起始频率 f0=76f_0=76f0=76 GHz,干扰雷达 fI=76.1f_I=76.1fI=76.1 GHz;斜率分别为 u=20u=20u=20 MHz/µs 与 uI=16u_I=16uI=16 MHz/µs;采样时长 51.2 µs,复采样率 20 MHz;目标对应"60 m / 8 MHz"的拍频;高斯窗主瓣3dB宽度设置为 2.35 µs,滑动步长 1.5 µs。
这些参数组合意味着互扰去斜项的斜率 u−uI≠0u-u_I\neq 0u−uI=0,属于典型"扫频互扰"场景。
5.2 指标定义:SIR与PSD
文中将IF域回波功率与互扰功率之比定义为SIR(尽管符号写作signal-to-noise ratio,但语义是signal-to-interference ratio)。同时定义成功检测概率PSD:在多次实验中,检测频率误差小于0.5%的次数占比。
5.3 图5:干扰抬升频谱底噪,但峰累积仍凸显目标频率
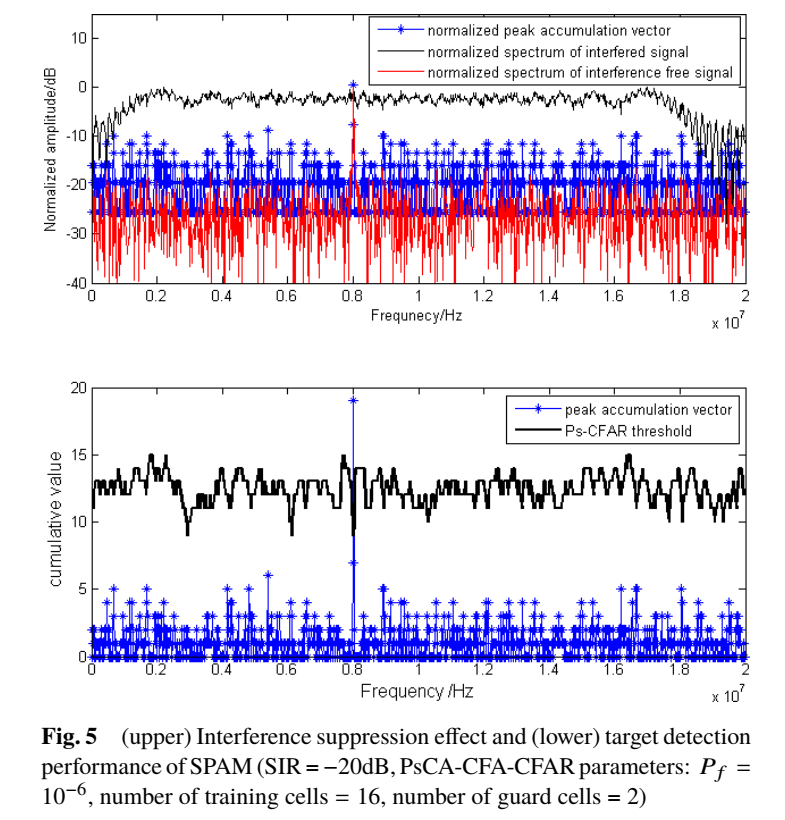
图5上图同时画出了:互扰条件下的归一化频谱、无干扰时的归一化频谱,以及峰累积向量(以离散点/茎状形式)。可以直观看到互扰使频谱底噪显著抬升,从"幅度谱"角度很难稳定检出目标;但峰累积向量在目标拍频位置形成显著尖峰,等价于把检测域从"幅度高度"迁移到"峰出现次数"。
图5下图则给出Ps-CFAR阈值与峰累积向量对比:目标尖峰越过门限完成检测。图注中给定的典型参数为 Pf=10−6P_f=10^{-6}Pf=10−6,训练单元16、保护单元2,SIR = −20 dB。
5.4 图6:SPAM在低SIR下相对传统CA-CFAR的优势
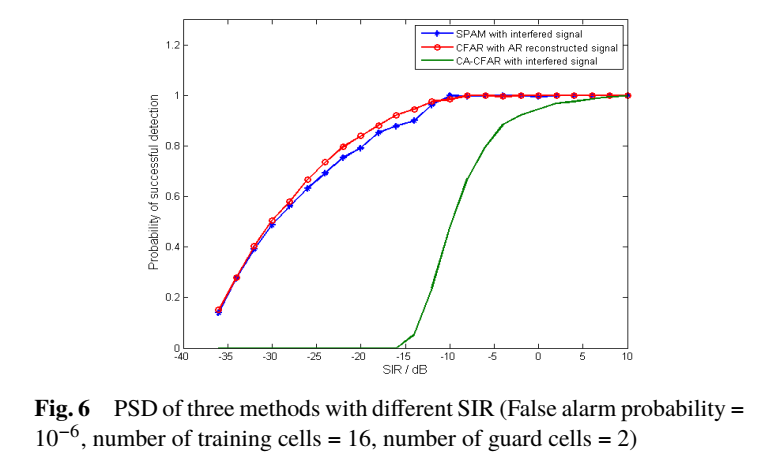
图6对比三种方法:
(1) 直接在互扰信号上做CA-CFAR;
(2) 先用AR模型重构信号再做CA-CFAR;
(3) SPAM直接在互扰信号上检测。
曲线显示:在相同虚警概率与训练/保护单元设置下,SPAM与"AR重构+CA-CFAR"的检测性能处于同一量级;而相对"不做抑制的传统检测",两者在达到同等PSD要求时可提升约15--20 dB的互扰容忍度。文中还强调当SIR低于−20 dB时,检测精度(文中用"accuracy"表述)仍可保持在95%以上。
6. 计算复杂度:为何说"快"
文中认为SPAM的主要计算量集中在Gabor变换,其余部分(峰搜索、计数、Ps-CFAR)是一维线性复杂度 O(N)O(N)O(N) 级别。对长度为 NNN 的时域采样序列,若窗函数滑动步长为 TstepT_{step}Tstep,文中给出Gabor变换的复乘代价估计:
Cost≈N2log2(N)2Tstep \text{Cost}\approx \frac{N^2\log_2(N)}{2T_{step}} Cost≈2TstepN2log2(N)
并指出这只比短时傅里叶变换略高;同时由于无需做干扰压制与信号重构,总体计算量显著小于同类"抑制+重构"方案。
需要注意的是:该复杂度写法反映的是一种"按滑窗次数 × 每窗FFT代价"的量级估算,严格推导要明确窗长、窗数与FFT点数的取值关系(附录会给出一种与该形式一致的推导路径)。
7. 方法特征与适用边界(客观讨论)
SPAM的本质是把检测问题从"幅度统计"转为"结构统计":用峰位置的稀疏二值化削弱互扰功率优势,再用列累积把目标的"稳定频率"特征放大到可检测的统计显著性上。其效果依赖于两个前提:一是目标回波在多个时窗内能形成相对稳定的局部峰;二是互扰峰位置在时间上更分散,使得背景列计数可用泊松模型刻画并与目标尖峰区分。
同时,文中对"平行干扰"(uI=uu_I=uuI=u)认为可忽略,这意味着算法主要面向更常见的扫频互扰情形;若平行干扰占比上升或存在更复杂体制(如多斜率、多chirp编排),峰分布形态与背景统计可能需要重新评估。
附录A:文中省略的推导补全(围绕式(1)--(8)展开)
A.1 由式(1)(2)推到"拍频近似常数"的形式
为突出单目标情形,先取式(2)中单一散射体(忽略下标 iii):
Secho(t)=a Str(t−Δτ). S_{echo}(t)=a\,S_{tr}(t-\Delta\tau). Secho(t)=aStr(t−Δτ).
由式(1)得
Str(t−Δτ)=exp{j2π[f0(t−Δτ)+12u(t−Δτ)2]}. S_{tr}(t-\Delta\tau)=\exp\left\{j2\pi\left[f_0(t-\Delta\tau)+\frac12 u(t-\Delta\tau)^2\right]\right\}. Str(t−Δτ)=exp{j2π[f0(t−Δτ)+21u(t−Δτ)2]}.
去斜(dechirp)相当于用本振/参考chirp的共轭相乘(与式(4)一致),对回波项有:
SIF,echo(t)=Str(t)⋅Secho∗(t)=a∗ Str(t)⋅Str∗(t−Δτ). S_{IF,echo}(t)=S_{tr}(t)\cdot S_{echo}^*(t)=a^*\,S_{tr}(t)\cdot S_{tr}^*(t-\Delta\tau). SIF,echo(t)=Str(t)⋅Secho∗(t)=a∗Str(t)⋅Str∗(t−Δτ).
将式(1)代入并合并指数:
SIF,echo(t)=a∗exp{j2π[f0t+12ut2]}exp{−j2π[f0(t−Δτ)+12u(t−Δτ)2]}=a∗exp{j2π(f0t−f0(t−Δτ)+12ut2−12u(t−Δτ)2)}. \begin{aligned} S_{IF,echo}(t) &=a^* \exp\left\{j2\pi\left[f_0 t+\frac12 u t^2\right]\right\} \exp\left\{-j2\pi\left[f_0(t-\Delta\tau)+\frac12 u(t-\Delta\tau)^2\right]\right\}\\ &=a^*\exp\left\{j2\pi\Big(f_0 t-f_0(t-\Delta\tau)+\frac12 u t^2-\frac12 u(t-\Delta\tau)^2\Big)\right\}. \end{aligned} SIF,echo(t)=a∗exp{j2π[f0t+21ut2]}exp{−j2π[f0(t−Δτ)+21u(t−Δτ)2]}=a∗exp{j2π(f0t−f0(t−Δτ)+21ut2−21u(t−Δτ)2)}.
展开平方项:
(t−Δτ)2=t2−2tΔτ+(Δτ)2. (t-\Delta\tau)^2=t^2-2t\Delta\tau+(\Delta\tau)^2. (t−Δτ)2=t2−2tΔτ+(Δτ)2.
于是
12ut2−12u(t−Δτ)2=12ut2−12u(t2−2tΔτ+(Δτ)2)=utΔτ−12u(Δτ)2. \frac12 u t^2-\frac12 u(t-\Delta\tau)^2 =\frac12 u t^2-\frac12 u\left(t^2-2t\Delta\tau+(\Delta\tau)^2\right) =u t\Delta\tau-\frac12 u(\Delta\tau)^2. 21ut2−21u(t−Δτ)2=21ut2−21u(t2−2tΔτ+(Δτ)2)=utΔτ−21u(Δτ)2.
而
f0t−f0(t−Δτ)=f0Δτ. f_0 t-f_0(t-\Delta\tau)=f_0\Delta\tau. f0t−f0(t−Δτ)=f0Δτ.
代回可得
SIF,echo(t)=a∗exp{j2π[uΔτ⏟fb t+(f0Δτ−12u(Δτ)2)]}. S_{IF,echo}(t)=a^*\exp\left\{j2\pi\left[\underbrace{u\Delta\tau}_{f_b}\,t+\left(f_0\Delta\tau-\frac12 u(\Delta\tau)^2\right)\right]\right\}. SIF,echo(t)=a∗exp⎩ ⎨ ⎧j2π fb uΔτt+(f0Δτ−21u(Δτ)2) ⎭ ⎬ ⎫.
这表明回波去斜后的主要相位是线性项 2πfbt2\pi f_b t2πfbt,其"拍频":
fb=uΔτ. f_b=u\Delta\tau. fb=uΔτ.
若进一步引入FMCW通用关系(行业常规展开)Δτ=2R/c\Delta\tau=2R/cΔτ=2R/c,则
fb=2uRc, f_b=\frac{2uR}{c}, fb=c2uR,
拍频与距离成正比。式(4)中用 fbi(t)f_{b_i}(t)fbi(t) 表示"拍频信号",在上述推导下其可以视作(忽略常相位):
fb(t)∝exp(j2πfbt), f_{b}(t)\propto \exp(j2\pi f_b t), fb(t)∝exp(j2πfbt),
实信号形式对应余弦。
A.2 由式(1)(3)(4)推到"扫频互扰斜率为 u−uIu-u_Iu−uI"并解释其"铺满频带"的原因
互扰去斜项定义为
SMI(t)=p Str(t) SI∗(t). S_{MI}(t)=p\,S_{tr}(t)\,S_I^*(t). SMI(t)=pStr(t)SI∗(t).
由式(3)可写互扰信号(省略常量相位):
SI(t)=exp{j2π[fI(t−Δt)+12uI(t−Δt)2]}. S_I(t)=\exp\left\{j2\pi\left[f_I(t-\Delta t)+\frac12 u_I(t-\Delta t)^2\right]\right\}. SI(t)=exp{j2π[fI(t−Δt)+21uI(t−Δt)2]}.
因此
SI∗(t)=exp{−j2π[fI(t−Δt)+12uI(t−Δt)2]}. S_I^*(t)=\exp\left\{-j2\pi\left[f_I(t-\Delta t)+\frac12 u_I(t-\Delta t)^2\right]\right\}. SI∗(t)=exp{−j2π[fI(t−Δt)+21uI(t−Δt)2]}.
将式(1)与上式相乘:
SMI(t)=pexp{j2π(f0t+12ut2)}exp{−j2π[fI(t−Δt)+12uI(t−Δt)2]}=pexp{j2πΦ(t)}, \begin{aligned} S_{MI}(t) &=p\exp\left\{j2\pi\left(f_0 t+\frac12 u t^2\right)\right\} \exp\left\{-j2\pi\left[f_I(t-\Delta t)+\frac12 u_I(t-\Delta t)^2\right]\right\}\\ &=p\exp\left\{j2\pi\Phi(t)\right\}, \end{aligned} SMI(t)=pexp{j2π(f0t+21ut2)}exp{−j2π[fI(t−Δt)+21uI(t−Δt)2]}=pexp{j2πΦ(t)},
其中相位
Φ(t)=f0t+12ut2−fI(t−Δt)−12uI(t−Δt)2. \Phi(t)=f_0 t+\frac12 u t^2-f_I(t-\Delta t)-\frac12 u_I(t-\Delta t)^2. Φ(t)=f0t+21ut2−fI(t−Δt)−21uI(t−Δt)2.
将 (t−Δt)2=t2−2tΔt+(Δt)2(t-\Delta t)^2=t^2-2t\Delta t+(\Delta t)^2(t−Δt)2=t2−2tΔt+(Δt)2 展开:
Φ(t)=f0t+12ut2−fIt+fIΔt−12uIt2+uItΔt−12uI(Δt)2=(12(u−uI))t2⏟二次相位+[(f0−fI)+uIΔt]t⏟一次相位+(fIΔt−12uI(Δt)2)⏟常相位. \begin{aligned} \Phi(t) &=f_0 t+\frac12 u t^2-f_I t+f_I\Delta t-\frac12 u_I t^2+u_I t\Delta t-\frac12 u_I(\Delta t)^2\\ &=\underbrace{\left(\frac12(u-u_I)\right)t^2}{\text{二次相位}} +\underbrace{\left[(f_0-f_I)+u_I\Delta t\right]t}{\text{一次相位}} +\underbrace{\left(f_I\Delta t-\frac12 u_I(\Delta t)^2\right)}_{\text{常相位}}. \end{aligned} Φ(t)=f0t+21ut2−fIt+fIΔt−21uIt2+uItΔt−21uI(Δt)2=二次相位 (21(u−uI))t2+一次相位 [(f0−fI)+uIΔt]t+常相位 (fIΔt−21uI(Δt)2).
瞬时频率为相位对时间的一阶导数:
fMI(t)=dΦ(t)dt=(u−uI)t+[(f0−fI)+uIΔt]. f_{MI}(t)=\frac{d\Phi(t)}{dt}=(u-u_I)t+\big[(f_0-f_I)+u_I\Delta t\big]. fMI(t)=dtdΦ(t)=(u−uI)t+[(f0−fI)+uIΔt].
这说明当 uI≠uu_I\neq uuI=u 时,互扰去斜项的瞬时频率随时间线性变化,其"扫频斜率"确为
dfMI(t)dt=u−uI, \frac{df_{MI}(t)}{dt}=u-u_I, dtdfMI(t)=u−uI,
与文中描述一致。由于接收链路的低通滤波器会截断超过 fcutofff_{\text{cutoff}}fcutoff 的成分,因此在"扫频穿越IF带宽"的过程中,互扰表现为在某些时间段进入IF通带、在某些时间段离开通带;从频域整体观察,它会把能量散布到IF的较大范围并抬升频谱底噪,这就是"扫频互扰更关键"的原因。
当 uI=uu_I=uuI=u 时,上式退化为
fMI(t)=(f0−fI)+uΔt, f_{MI}(t)=(f_0-f_I)+u\Delta t, fMI(t)=(f0−fI)+uΔt,
成为近似常频分量,对应文中的"平行干扰"。
A.3 式(5)的离散化:从积分到"时频矩阵 GGG"
对采样信号 SIF[n]=SIF(nTs)S_{IF}[n]=S_{IF}(nT_s)SIF[n]=SIF(nTs)(采样周期 TsT_sTs),将式(5)离散化,若取窗函数中心位于 τ=mTstep\tau=mT_{\text{step}}τ=mTstep(滑动步长 TstepT_{\text{step}}Tstep),则
G[m,k]=∑n=0N−1SIF[n] gσ∗ ((nTs−mTstep)) e−j2πkn/N, G[m,k]=\sum_{n=0}^{N-1} S_{IF}[n]\; g_\sigma^*\!\big((nT_s-mT_{\text{step}})\big)\;e^{-j2\pi kn/N}, G[m,k]=n=0∑N−1SIF[n]gσ∗((nTs−mTstep))e−j2πkn/N,
其中 kkk 是离散频率索引。对每个 mmm 做一次FFT即可得到该时刻的频谱切片,堆叠后形成 G∈CM×NG\in\mathbb{C}^{M\times N}G∈CM×N。这与文中"Performing discrete Gabor transformation... the time-frequency matrix GGG can be obtained"一致,只是文中为简洁省略了离散化细节。
A.4 "高斯主瓣3dB宽度"与 σ\sigmaσ 的严格关系
文中给出 2.4≈22ln22.4\approx 2\sqrt{2\ln2}2.4≈22ln2 并把它与高斯主瓣3dB宽度联系起来。下面给出常见严格关系之一(在时域幅度意义下)。
对高斯窗
gσ(t)=exp(−t22σ2), g_\sigma(t)=\exp\left(-\frac{t^2}{2\sigma^2}\right), gσ(t)=exp(−2σ2t2),
其最大值在 t=0t=0t=0 为1。3dB点通常指幅度降为 1/21/\sqrt{2}1/2 (功率降为1/2)的位置,即解:
exp(−t22σ2)=12. \exp\left(-\frac{t^2}{2\sigma^2}\right)=\frac{1}{\sqrt2}. exp(−2σ2t2)=2 1.
两边取对数:
−t22σ2=−12ln2⇒t=σln2. -\frac{t^2}{2\sigma^2}=-\frac12\ln2 \quad\Rightarrow\quad t=\sigma\sqrt{\ln2}. −2σ2t2=−21ln2⇒t=σln2 .
因此双边3dB宽度(从 −t-t−t 到 +t+t+t)为
W3dB=2σln2≈1.665 σ. W_{3dB}=2\sigma\sqrt{\ln2}\approx 1.665\,\sigma. W3dB=2σln2 ≈1.665σ.
若改用"功率3dB宽度"定义(即 gσ2(t)=1/2g_\sigma^2(t)=1/2gσ2(t)=1/2),则解
exp(−t2σ2)=12⇒t=σln2⇒W3dB=2σln2 \exp\left(-\frac{t^2}{\sigma^2}\right)=\frac12 \Rightarrow t=\sigma\sqrt{\ln2} \Rightarrow W_{3dB}=2\sigma\sqrt{\ln2} exp(−σ2t2)=21⇒t=σln2 ⇒W3dB=2σln2
与上式相同。
而文中出现的 22ln2≈2.35482\sqrt{2\ln2}\approx 2.354822ln2 ≈2.3548 更常见于"高斯分布的FWHM(半高全宽)"在另一种参数化下的表达:若采用
g(t)=exp(−t22s2), g(t)=\exp\left(-\frac{t^2}{2s^2}\right), g(t)=exp(−2s2t2),
则其半高(幅度=1/2)解满足
exp(−t22s2)=12⇒t=s2ln2⇒FWHM=2s2ln2≈2.3548 s. \exp\left(-\frac{t^2}{2s^2}\right)=\frac12 \Rightarrow t=s\sqrt{2\ln2} \Rightarrow \text{FWHM}=2s\sqrt{2\ln2}\approx 2.3548\,s. exp(−2s2t2)=21⇒t=s2ln2 ⇒FWHM=2s2ln2 ≈2.3548s.
可见"系数2.3548"对应的是"幅度半高"的宽度而非"3dB(幅度 1/21/\sqrt21/2 )"。文中把它称作3dB宽度,可能是将"半高宽"与"3dB宽"在工程语境中合并使用或存在记号上的简化。无论采用哪一种宽度定义,核心逻辑是一致的:σ\sigmaσ 决定窗宽,窗宽决定时频分辨率折中,经验上取 σ∝B/u\sigma\propto B/uσ∝B/u 以匹配系统扫频速度与IF带宽尺度。
A.5 为什么列累积 C[n]C[n]C[n] 可近似泊松:从二项分布到泊松极限
文中给出"列方向峰计数先服从二项分布,再近似泊松"的一句话式推理,这里补全一个典型推导框架。
设在无目标背景下,对固定频率bin nnn,每个时间窗(每一行)是否在该bin产生"被选中的谱峰"可视为一个伯努利随机变量:
Bm(n)={1,第 m 行在频率 n 处产生谱峰0,否则 B_m(n)= \begin{cases} 1,& \text{第 }m\text{ 行在频率 }n\text{ 处产生谱峰}\\ 0,& \text{否则} \end{cases} Bm(n)={1,0,第 m 行在频率 n 处产生谱峰否则
假设各时间窗之间近似独立、且成功概率为 pnp_npn(背景统计缓慢变化时可近似常数),则列累积
C(n)=∑m=1MBm(n) C(n)=\sum_{m=1}^{M}B_m(n) C(n)=m=1∑MBm(n)
服从二项分布:
C(n)∼Binomial(M,pn). C(n)\sim\text{Binomial}(M,p_n). C(n)∼Binomial(M,pn).
当 MMM 较大且 pnp_npn 较小("峰事件稀疏"),并令 λn=Mpn\lambda_n=M p_nλn=Mpn 为有限常数,则二项分布满足泊松极限:
limM→∞, pn→0, Mpn=λn(Mk)pnk(1−pn)M−k=λnkk!e−λn. \lim_{M\to\infty,\,p_n\to 0,\,Mp_n=\lambda_n} \binom{M}{k}p_n^k(1-p_n)^{M-k} =\frac{\lambda_n^k}{k!}e^{-\lambda_n}. M→∞,pn→0,Mpn=λnlim(kM)pnk(1−pn)M−k=k!λnke−λn.
于是
C(n)≈Poisson(λn). C(n)\approx \text{Poisson}(\lambda_n). C(n)≈Poisson(λn).
文中使用单一参数 λ\lambdaλ 描述背景,等价于在频率方向上假设 pnp_npn 近似相同或用训练单元局部平均估计得到局部 λ\lambdaλ。这也解释了为何在Ps-CFAR实现中需要训练单元对背景统计进行估计:目标频率附近的背景可能并非全局平稳。
A.6 由式(7)(8)构造门限的计算细节:分位数、近似与快速实现
式(8)要求解最小整数 hhh 使得
F(h;λ)=∑k=0hλkk!e−λ≥1−Pf, F(h;\lambda)=\sum_{k=0}^{h}\frac{\lambda^k}{k!}e^{-\lambda}\ge 1-P_f, F(h;λ)=k=0∑hk!λke−λ≥1−Pf,
即
h=F−1(1−Pf;λ). h = F^{-1}(1-P_f;\lambda). h=F−1(1−Pf;λ).
在工程实现中常见三种路径:
第一种是直接递推累加泊松概率直到达到 1−Pf1-P_f1−Pf。利用递推关系
P{x=k+1}=λk+1P{x=k}, P\{x=k+1\}=\frac{\lambda}{k+1}P\{x=k\}, P{x=k+1}=k+1λP{x=k},
可从 k=0k=0k=0 开始迭代,避免重复计算阶乘。
第二种是正态近似(当 λ\lambdaλ 不太小)。由于泊松满足均值方差同为 λ\lambdaλ,可近似
x≈N(λ,λ). x\approx \mathcal{N}(\lambda,\lambda). x≈N(λ,λ).
令 z1−Pfz_{1-P_f}z1−Pf 为标准正态分位数,则可取
h≈λ+z1−Pfλ, h \approx \lambda + z_{1-P_f}\sqrt{\lambda}, h≈λ+z1−Pfλ ,
再向上取整并可用精确尾概率校正一步。对于文中常用极低虚警 Pf=10−6P_f=10^{-6}Pf=10−6,z1−Pfz_{1-P_f}z1−Pf 较大,此近似仍可作为初值。
第三种是Chernoff界/大偏差近似。求满足
P{x≥h}≤Pf P\{x\ge h\}\le P_f P{x≥h}≤Pf
的 hhh,可用泊松的Chernoff上界:
P{x≥(1+δ)λ}≤(eδ(1+δ)1+δ)λ. P\{x\ge (1+\delta)\lambda\}\le \left(\frac{e^\delta}{(1+\delta)^{1+\delta}}\right)^\lambda. P{x≥(1+δ)λ}≤((1+δ)1+δeδ)λ.
给定 PfP_fPf 与 λ\lambdaλ,可先解 δ\deltaδ,再取 h=⌈(1+δ)λ⌉h=\lceil(1+\delta)\lambda\rceilh=⌈(1+δ)λ⌉。这种方法偏保守,但在极低虚警下稳定。
文中没有展开"训练单元与保护单元如何估计 λ\lambdaλ"的具体式子。一个与CA-CFAR一致的局部估计写法是:对被检单元(CUT)周围,跳过保护单元,在两侧训练单元上取平均:
λ^=1NT∑n∈TC[n], \hat\lambda=\frac{1}{N_T}\sum_{n\in\mathcal{T}} C[n], λ^=NT1n∈T∑C[n],
其中 T\mathcal{T}T 为训练单元索引集合,NT=∣T∣N_T=|\mathcal{T}|NT=∣T∣。然后用 λ^\hat\lambdaλ^ 代入式(8)求阈值 hhh,再比较 C[CUT]C[\text{CUT}]C[CUT] 与 hhh。
A.7 文中复杂度表达式的一种一致推导
文中给出Gabor变换复杂度约为
N2log2(N)2Tstep \frac{N^2\log_2(N)}{2T_{step}} 2TstepN2log2(N)
次复乘。下面给出一种能产生同型表达的推导方式(强调量级一致而非唯一形式)。
设时域采样点数为 NNN,每次窗内做 NNN 点FFT(或零填充到同阶),则单窗FFT复杂度为 O(Nlog2N)O(N\log_2 N)O(Nlog2N)。若窗中心以步长 TstepT_{step}Tstep 滑动,窗数 MMM 与总时长 TTT 成正比:M≈T/TstepM\approx T/T_{step}M≈T/Tstep。在离散域,T≈NTsT\approx NT_sT≈NTs,于是
M≈NTsTstep. M\approx \frac{NT_s}{T_{step}}. M≈TstepNTs.
总复杂度量级
O(M⋅Nlog2N)=O(NTsTstep⋅Nlog2N)=O(N2log2NTstep), O\left(M\cdot N\log_2 N\right) =O\left(\frac{NT_s}{T_{step}}\cdot N\log_2 N\right) =O\left(\frac{N^2\log_2 N}{T_{step}}\right), O(M⋅Nlog2N)=O(TstepNTs⋅Nlog2N)=O(TstepN2log2N),
与文中形式一致,仅差一个常数系数(文中给出"/2",可理解为复乘计数口径、实/复FFT常数、或窗有效长度等因素合并后的系数)。