sklearn函数总结九— 朴素贝叶斯

纯手打，代码整理中，持续更新中^-^

序号延用总结八

目录

16、朴素贝叶斯

[16.1 什么是贝叶斯公式？](#16.1 什么是贝叶斯公式？)

这些符号是什么意思？

我们来推导一下贝叶斯公式

[16.2 贝叶斯公式经典实例：疾病的检测](#16.2 贝叶斯公式经典实例：疾病的检测)

场景：

问题：

结论：

[16.3 什么是朴素贝叶斯算法？](#16.3 什么是朴素贝叶斯算法？)

[16.4 朴素贝叶斯的优缺点](#16.4 朴素贝叶斯的优缺点)

优点：

缺点：

[16.5 代码示例-新闻文本分类预测](#16.5 代码示例-新闻文本分类预测)

[16.6 参数详解](#16.6 参数详解)

参数详解：

[1. alpha : float, 默认=1.0](#1. alpha : float, 默认=1.0)

[2. fit_prior : bool, 默认=True](#2. fit_prior : bool, 默认=True)

[3. class_prior : array-like of shape (n_classes,), 默认=None](#3. class_prior : array-like of shape (n_classes,), 默认=None)

---

16、朴素贝叶斯

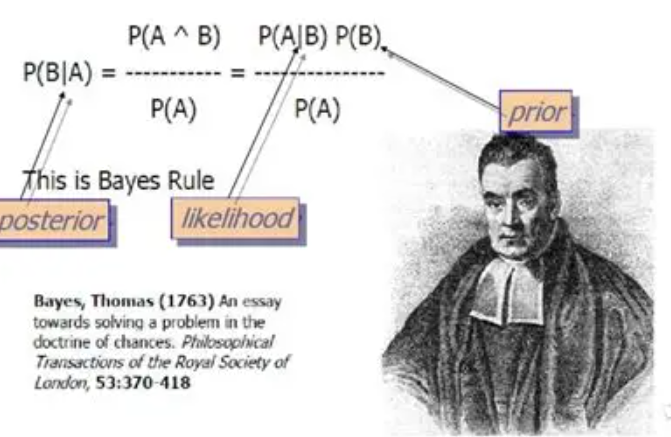
16.1 什么是贝叶斯公式？

在学习朴素贝叶斯之前，我们必须要先掌握贝叶斯公式：

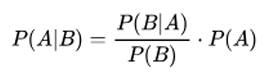
这个公式乍一看，你肯定很懵逼，不过不用怕，我们来解释和分解下，你就懂了。

这些符号是什么意思？

• P(A|B) ：在 B 已经发生的情况下，A 发生的概率。这是我们要找的，叫做后验概率（更新后的信念）。

• P(B|A) ：在 A 已经发生的情况下，B 发生的概率。这个通常我们从数据中能得到，叫做似然概率。

• P(A) ：在不知道任何证据（B）的情况下，A 发生的概率。这是我们最初的看法，叫做先验概率。

• P(B)：B 发生的总概率，叫做证据或标准化常量。

我们来推导一下贝叶斯公式

1.P(AB) = P(A) * P(B|A)

A 和 B 同时发生的概率等于 P(A) 乘以 P(B|A)，这个大家应该能理解。

2、同理 P(AB) = P(B) * P(A|B)

A 和 B 同时发生的概率也等于 P(B) 乘以 P(A|B)，相信这个大家也应该能理解。

3、 所以我们能推导出：

P(A) * P(B|A) = P(B) * P(A|B)

把右边的 P(B) 放到左边去，就推导出了贝叶斯公式。相当大家彻底理解了贝叶斯公式。

16.2 贝叶斯公式经典实例：疾病的检测

这是一个非常著名且反直觉的例子，能完美展示贝叶斯思想的威力。

场景：

假设某种疾病在人群中的发病率是 1%（先验知识）。现在有一种检测方法：

• 如果你确实有病，检测结果呈阳性（True Positive）的概率是 99%（非常准）。

• 如果你没有病，检测结果呈阳性（False Positive）的概率是 5%（有5%的误诊率）。

问题：

如果一个人去做了检测，结果是阳性，那么他真正患病的概率到底是多少？

---

很多人会直觉地认为是 99% 或者 95%，但贝叶斯定理会给我们一个出乎意料的答案。

首先，定义事件：

• A：真正患病

• B：检测结果为阳性

我们要求的是：在检测结果为阳性的情况下，真正患病的概率，即 P(患病 | 阳性)，也就是 P(A|B)。

根据公式，我们需要知道：

1. P(A) - 先验概率：在不知道检测结果时，一个人患病的概率 = 发病率 = 1% = 0.01

2. P(B|A) - 似然概率：如果一个人真有病，检测为阳性的概率 = 99% = 0.99

3. P(B) - 证据：检测结果为阳性的总概率。这个需要计算一下。

计算 P(B)：一个人检测为阳性有两种可能：

• 他真有病，并且检测对了：(0.01 * 0.99)

• 他其实没病，但被误诊了：((1 - 0.01) * 0.05)

所以，

P(B) = （真有病且测出阳性）+ （真没病但误诊为阳性）

P(B) = (0.01 * 0.99) + (0.99 * 0.05)

P(B) = 0.0099 + 0.0495

P(B) = 0.0594

现在，将所有值代入贝叶斯公式：

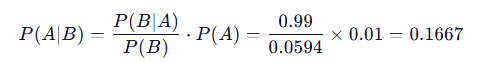
结论：

即使检测结果是阳性，你真正患病的概率也只有大约 16.67%！

16.3 什么是朴素贝叶斯算法？

朴素贝叶斯（Naive Bayes）算法 是一种基于贝叶斯定理的分类方法，广泛应用于文本分类（如垃圾邮件识别、情感分析等）和其他机器学习领域。

它的核心假设是：

特征与特征之间条件相互独立，即在给定类别的条件下，特征之间没有任何关系或依赖。

公式数学推导略

16.4 朴素贝叶斯的优缺点

优点：

1. 简洁高效：朴素贝叶斯方法实现简单，训练和预测速度都非常快。

2. 适合高维数据：对于特征维度很高的数据（如文本分类），朴素贝叶斯特别适用，因为它能有效处理大量的特征。

3. 良好的性能：在许多实际问题中，朴素贝叶斯能够取得不错的分类效果，特别是在数据特征间独立性假设基本成立的情况下。

缺点：

1. 条件独立假设过于简单：实际数据中，特征之间往往存在依赖关系，而朴素贝叶斯假设特征之间完全独立，这可能会影响其性能。

2. 对稀疏数据敏感：如果某个类别中某个特征从未出现过，朴素贝叶斯会计算出零概率，导致预测失败。为了解决这个问题，通常采用平滑技术（如拉普拉斯平滑）来避免零概率的问题。

16.5 代码示例-新闻文本分类预测

from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import TfidfVectorizer

from sklearn.metrics import accuracy_score, classification_report
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import MultinomialNB


# 1, 加载数据
news = fetch_20newsgroups(subset='all')

# 2, 数据预处理
X_train, X_test, y_train, y_test = train_test_split(
    news.data, news.target, test_size=0.2
)  # 划分训练集和测试集

tfidfvectorizer = TfidfVectorizer()  # 特征抽取 TF-IDF
X_train_scaled = tfidfvectorizer.fit_transform(X_train)  # fit计算生成模型
X_test_scaled = tfidfvectorizer.transform(X_test)  # 使用训练集的参数转换测试集

# 3, 创建和训练 LogisticRegression 模型
model = MultinomialNB()
model.fit(X_train_scaled, y_train)  # 使用训练数据拟合（训练）模型

# 4, 进行预测并评估模型
y_pred = model.predict(X_test_scaled)  # 在测试集上进行预测
print('模型预测值: ', y_pred)
print('正确值    : ', y_test)

accuracy = accuracy_score(y_test, y_pred)  # 计算准确率
print(f'测试集准确率: {accuracy:.2f}')

print('分类报告: \n', classification_report(y_test, y_pred,
                                            target_names=news.target_names))

输出

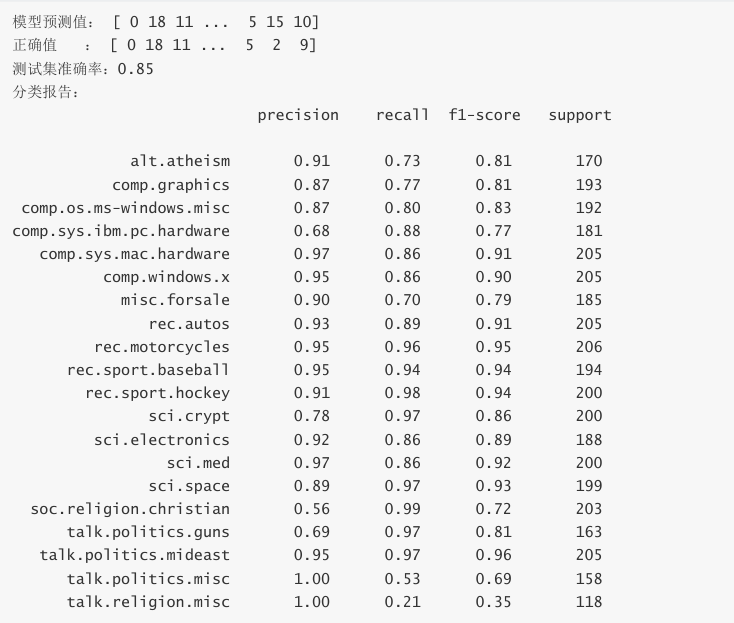
16.6 参数详解

MultinomialNB 是 Scikit-learn 中用于多项式分布数据的朴素贝叶斯分类器，特别适合文本分类等离散特征计数的场景。下面详细解释其构造方法、参数、属性和方法。

MultinomialNB(alpha=1.0, fit_prior=True, class_prior=None)

参数详解：

1. alpha : float, 默认=1.0

• 含义：平滑参数（拉普拉斯平滑/Lidstone平滑）

• 作用：防止概率计算中出现零值的问题

• 详细解释：

  • 当某个特征在某个类别中从未出现时，概率会变为0，导致整个后验概率为0

  • alpha=1 是拉普拉斯平滑（加1平滑）

  • 0 < alpha < 1 是 Lidstone 平滑

  • alpha=0 表示不使用平滑（可能导致过拟合和零概率问题）

• 数学公式：

  • 平滑后的条件概率：P (xi ∣y )=N ⋅y +α ×nN ⋅{i }+α

  • 其中 N ⋅{i } 是特征 i 在类别 y 中的出现次数，N ⋅y 是类别 y 中所有特征的出现次数，n 是特征数量

• 建议值：通常使用1.0，可以通过交叉验证调整

---

2. fit_prior : bool, 默认=True

• 含义：是否学习类别先验概率

• 作用：控制是否使用训练数据中的类别分布

• 详细解释：

  • fit_prior=True：使用训练数据中的类别频率作为先验概率

  • fit_prior=False：使用均匀先验概率（所有类别概率相等）

• 数学公式：

  • 当 fit_prior=True：P (y )=NN ⋅y

  • 当 fit_prior=False：P (y )=k1 （k为类别数）

• 适用场景：

  • 当训练集类别分布能代表真实分布时，使用 True

  • 当训练集类别不平衡或不能代表真实分布时，可考虑使用 False

---

3. class_prior : array-like of shape (n_classes,), 默认=None

• 含义：类别的先验概率

• 作用：手动指定各类别的先验概率

• 详细解释：

  • 如果指定了此参数，fit_prior 参数将被忽略

  • 数组长度必须等于类别数量

  • 概率值应该总和为1（但算法会自动归一化）

• 示例：对于二分类问题，可以设置 class_prior=[0.7, 0.3]