均值向量的检验
阅读资料:
[一、"元" vs "因素"](#一、“元” vs “因素”)
[二、"水平" vs "样本"](#二、“水平” vs “样本”)
[三、固定因子 vs 随机因子 vs 协变量](#三、固定因子 vs 随机因子 vs 协变量)
情况三:多个总体的均值向量检验(多元方差分析,MANOVA)
一、"元" vs "因素"
- 元:指因变量 的数量。
(1)一元:1个因变量(如:只看"数学成绩")。
(2)多元:2个及以上因变量(如:同时看"数学成绩"和"物理成绩")。
- 因素:指自变量,通常是用来分组的类别变量。
(1)单因素:1个自变量(如:只按"性别"分组)。
(2)多因素:2个及以上自变量(如:同时按"性别"和"班级"分组)。
二、"水平" vs "样本"
- 水平:
一个因素的具体类别。例如,"性别"这个因素有"男"、"女"两个水平。
- 样本:
在T检验和方差分析的语境中,常指由某个因素水平划分出的组别。例如,"男性组"和"女性组"就是两个样本。
三、固定因子 vs 随机因子 vs 协变量
- 固定因子:
自变量的水平是研究者感兴趣的、固定的少数几个类别。例如,比较A、B、C三种特定的教学方法。
- 随机因子:
自变量的水平是从一个更大的总体中随机抽取的,研究目的不在于比较这些特定水平,而在于推断整个总体的变异。例如,从全国众多学校中随机抽取5所学校进行研究。
- 协变量:
在分析中需要控制其影响的连续型自变量。例如,在研究不同教学方法对学生成绩的影响时,学生的"入学前成绩"就是一个协变量。
四、为什么要做多元检验?(学习的动机)
缺陷一:忽略变量间相关性
一元检验将每个变量孤立看待,完全忽略了它们之间可能存在的相关关系。例如,一个人的数学成绩和物理成绩很可能正相关,单独检验会丢失这种重要信息。
缺陷二:增大整体第一类错误
第一类错误:原假设为真时,却错误地拒绝了它("弃真")。
如果对 p 个变量分别进行显著性水平为 α(如0.05)的一元检验,总的犯第一类错误的概率会远大于 α。这就像"常在河边走,哪有不湿鞋",检验次数多了,总有一次会犯错。
优势:可能提高统计功效
统计功效:原假设为假时,正确拒绝它的概率(1-β)。
有时,单个变量在组间的差异都不显著,但它们的联合效应却是显著的。
多元检验能捕捉到这种累积的、微弱但一致的信号,从而比一元检验更有可能发现真实的差异。
五、所有均值检验都遵循相同的逻辑框架。
核心逻辑:基于小概率原理的反证法
步骤1: 先假设原假设 H₀(如:两组均值相等)是正确的。
步骤2: 在此前提下,计算观测到当前样本数据或更极端数据的概率(即p值)。
步骤3: 如果这个概率非常小(p小于预设的显著性水平 α),就发生了"小概率事件"。我们宁愿相信数据,也不愿相信小概率事件会发生,因此拒绝 H₀。
步骤4: 如果这个概率不算是小概率,则不能拒绝 H₀(注意:这不等于接受 H₀)。
两类错误的权衡
α 与 β 的关系:在其他条件不变时,减小 α(要求更强的证据)会使 β 增大(更难发现真实差异),反之亦然。
要同时减小两者,最有效的方法是增加样本量。
六、多元均值检验的具体方法
情况一:单个总体的均值向量检验
检验一个样本的均值向量是否与某个已知的理论均值向量 μ₀ 存在显著差异。
前提假设:样本来自多元正态总体 N_p(μ, Σ)。
待检验假设:H₀: μ = μ₀ vs H₁: μ ≠ μ₀。
检验统计量:Hotelling's T²
当总体协方差矩阵 Σ 未知(更常见)时,使用样本协方差矩阵 S 代替,得到:
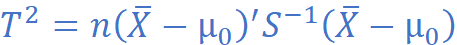
T² 服从 Hotelling's T² 分布,记为 T² ~ T²(p, n-p)。
如何决策?
T² 分布不常用,我们通常将其转换为熟悉的 F分布:
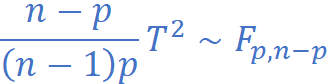
计算出F值后,查F分布表或由软件给出p值。若 p ≤ α,则拒绝 H₀。
情况二:两个总体的均值向量检验
比较两个独立样本或成对样本的均值向量是否存在显著差异。
两独立样本
场景:比较男性和女性在多个科目成绩上的平均差异。
前提假设:
两样本独立。
两总体均服从多元正态分布 N_p(μ₁, Σ) 和 N_p(μ₂, Σ)。
两总体具有相同的、未知的协方差矩阵 Σ。
待检验假设:H₀: μ₁ = μ₂ vs H₁: μ₁ ≠ μ₂。
检验统计量:
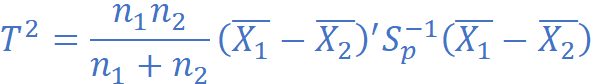
其中 S_p 是合并的协方差矩阵(综合两组数据的方差信息)。
与F分布的关系:
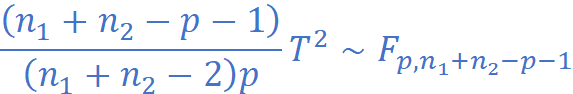
两成对样本
场景:比较同一批患者治疗前、后在多个健康指标上的变化。
数据转换:计算每对观测值的差值向量
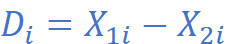
问题转换:将两样本检验问题转换为单样本检验问题,检验差值向量的均值 μ_D 是否为零向量。
检验统计量:
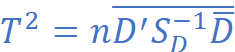
与F分布的关系:
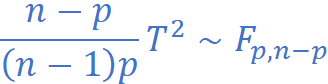
情况三:多个总体的均值向量检验(多元方差分析,MANOVA)
将单因素方差分析的思想推广到多元,用于比较三个或更多总体的均值向量。
基本思想:方差分解
总平方和与交叉积矩阵:T = SSP_total
组间SSP矩阵:B = SSP_between(由组间差异引起)
组内SSP矩阵:W = SSP_within(由组内个体差异引起)
关系:T = B + W
待检验假设:H₀: μ₁ = μ₂ = ... = μ_g vs H₁: 至少有两个均值向量不相等。
检验统计量:Wilk s 'Lambda Λ
定义:Λ = |W| / |T| = |W| / |B + W|
直观理解:Λ 的值域为 [0, 1]。当组间差异相对于组内差异非常大时,B 远大于 W,Λ 趋近于0,我们倾向于拒绝 H₀。
如何决策?
Λ 的精确分布复杂,通常将其转换为近似的 卡方分布 或 F分布。
卡方近似(大样本):
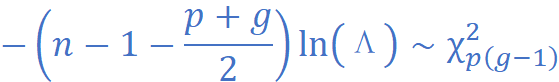
计算出卡方值后,查卡方分布表或由软件给出p值。
若 p ≤ α,则拒绝 H₀,表明至少有一对组的均值向量存在显著差异。
七、检验后操作
当多元检验拒绝了 H₀,我们只知道"各组不全相等",但更具体的问题随之而来。
变量差异
方法一:分别进行一元检验。对每个变量分别进行t检验或ANOVA。
校正 α:为控制整体第一类错误,需使用更严格的标准,如 Bonferroni校正,新的显著性水平为 α/p。
区分组别
方法二:Fisher判别函数。
目的:寻找一个原始变量的线性组合,使得不同组在该组合上的差异最大化,从而最好地区分各组。这是下一章"判别分析"的核心内容。