【LeetCode经典题解】：从前序和中序遍历构建二叉树详解

🎁个人主页：User_芊芊君子

🎉欢迎大家点赞👍评论📝收藏⭐文章

🔍系列专栏：Java.数据结构

【前言】

二叉树构造是算法中递归分治思想的经典应用，而通过前序与中序遍历序列还原二叉树，更是力扣考察二叉树特性的高频题。前序"根左右"、中序"左根右"的遍历特性，是逐层确定根节点、划分左右子树的关键。本文将从递归分治思想出发，拆解该问题的实现逻辑，分析代码设计的核心细节。

文章目录：

一、从前序遍历和中序遍历构造二叉树
二、思路分析
三、代码详解
- 1.代码分析
- 2.代码展示

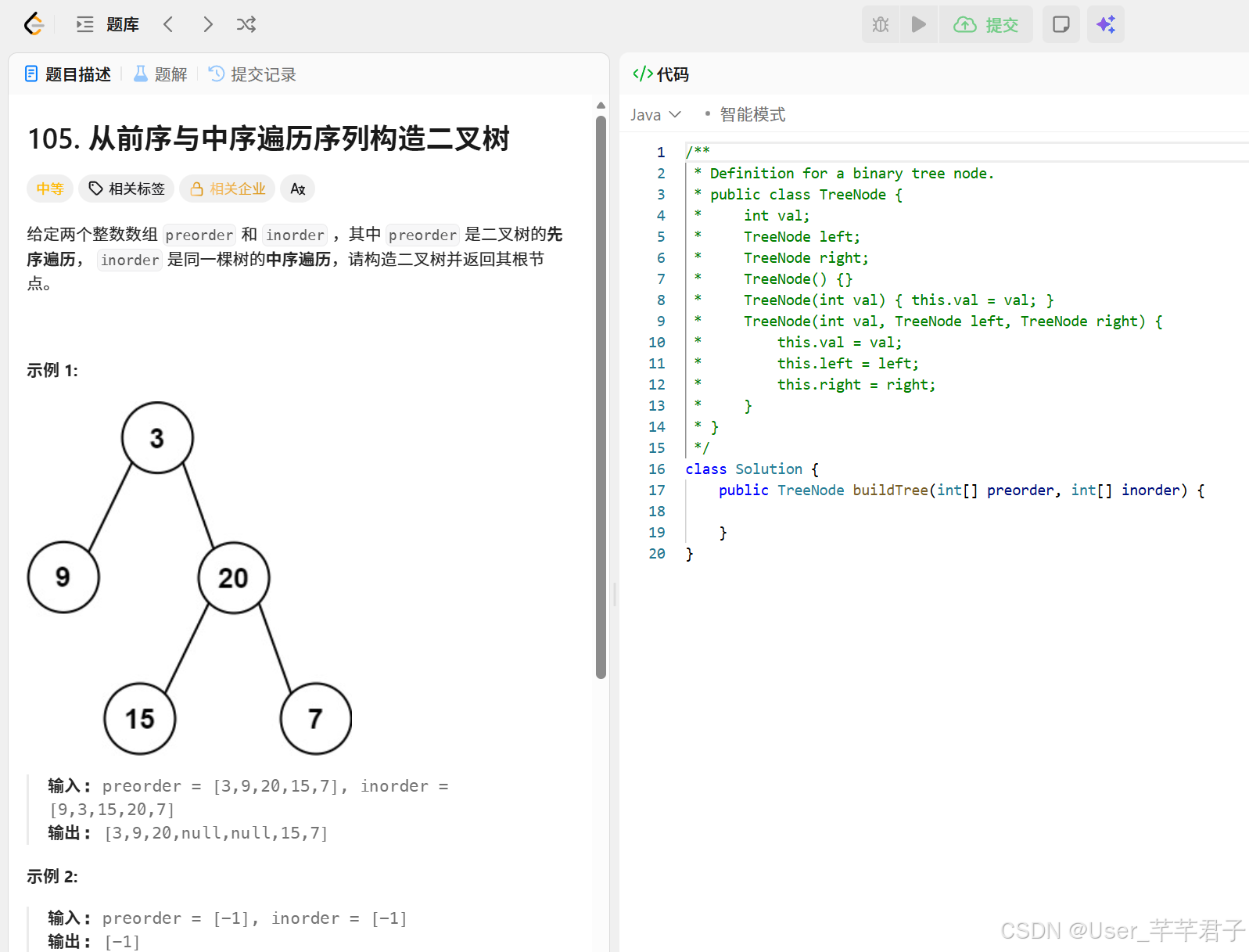
一、从前序遍历和中序遍历构造二叉树

链接直达：从前序遍历和中序遍历构造二叉树

二、思路分析

根据递归分治思想：

前序遍历：根节点--->左子树--->右子树；找到前序序列的第一个元素就是根节点；

中序遍历：左子树--->根节点--->右子树；找到根节点在中序序列中的位置，从而确定左子树和右子树；

递归处理：重复上面的步骤，依次确定子树的根节点并构建子树，直至子树为空。

三、代码详解

1.代码分析

preorder：前序遍历数组；
inorder : 中序遍历数组；
成员变量 preIndex : 用于记录前序遍历中当前根节点的索引（通过通过全局递增依次取前序序列的根节点）
findVal 方法：查找根节点在中序序列中的索引rootIndex；
递归方法buildTreeChild ：

递归终止条件：当 inbegin>inend ，说明当前子树无节点，返回null;

构建根节点，取前序数组preIndex位置的元素作为根节点；

划分左右子树，通过findVal方法找到根节点在中序序列中的索引rootIndex，inbegin ~ rootIndex-1为左子树，rootIndex+1 ~ inend为右子树

2.代码展示

java 复制代码

public int preIndex;
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        return buildTreeChild(preorder, inorder, 0 ,inorder.length-1);
    }
    public int findVal(int[] inorder,int inbegin,int inend,int key){
        for(int i = inbegin;i<=inend;i++){
            if(inorder[i]==key){
                return i;
            }
        }
        return -1;
    }
    public TreeNode buildTreeChild(int[] preorder, int[] inorder,int inbegin,int inend) {
        //递归终止条件：当前子树中序区间无节点
        if(inbegin>inend){
            return null;
        }
        //前序序列Index位置作为根节点
        TreeNode root = new TreeNode(preorder[preIndex]);
        //在中序序列中找到根节点的索引
        int rootIndex = findVal(inorder,inbegin,inend,preorder[preIndex]);
        //preIndex递增，指向下一个子树根节点
        preIndex++;
        //递归左子树，范围：inbegin ~ rootIndex-1
        root.left = buildTreeChild(preorder,inorder,inbegin,rootIndex-1);
        //递归左子树，范围：rootIndex+1 ~ inend
        root.right = buildTreeChild(preorder,inorder,rootIndex+1,inend);
        return root;
    }

【总结】

本文围绕前序+中序构建二叉树问题，解析了递归分治的解题思路：依托前序确定根节点，通过中序划分左右子树区间，再递归构建子树至区间为空。代码中用 prIndex 追踪前序根节点位置，借 findVal定位中序根节点索引完成边界划分，核心是对遍历特性的运用与递归终止条件的设置。此外，还可通过哈希表优化中序查找效率，该思路也为后序+中序构建二叉树等同类问题提供了参考。