计算机组成原理（6）：进位计数制

前言：

大家好，我是你们的老朋友。

在上一章的学习中，我们已经拥有了计算机的"上帝视角"：我们知道了冯·诺依曼架构下的五大金刚------运算器、控制器、存储器、输入设备、输出设备 。我们知道主存储器 （内存）里的 MAR （地址寄存器）决定了能存多少个数据，MDR（数据寄存器）决定了每个坑位能蹲多少个比特。

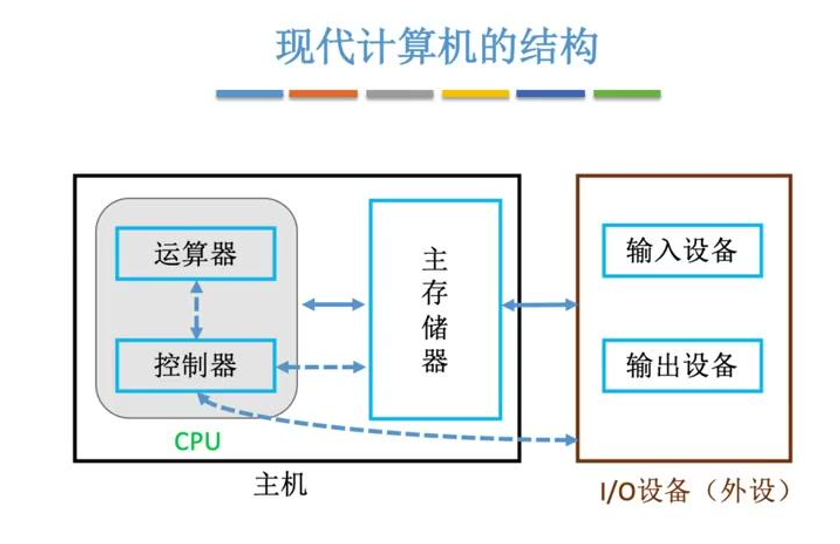
但是，那该死的求知欲在敲打着我们的脑壳：

"这些放在存储器里的数据，到底长什么样？"
"为什么计算机非要用 0 和 1？用 0-9 不香吗？"
"那个让我头秃的 16 进制，到底有什么用？"
"为什么 0.3 这个小数在计算机里存不准？"

这就引出了第二章的核心主题------数据的表示和运算。

这一章是整个计算机组成原理的"基石"。如果你连数字怎么表示都搞不清楚，后面讲 ALU（算术逻辑单元）如何做加法、讲浮点数为什么会溢出时，你绝对会一脸懵圈。

本篇文章是基础，希望能够帮助大家理解进位计数制的相关知识。

一、从远古部落到罗马帝国------计数的演变

1.1 最原始的"一维"计数法

想象一下，时光倒流回到几万年前的原始部落。你是部落里负责管果子的"仓库管理员"。

今天大家出去干活，带回来一堆苹果。你怎么记账？

那时候没有数字的概念，你大概率会拿出石刀，在墙壁上刻痕迹：

带回来一个苹果，画一条竖线 |。
又带回来一个，再画一条 ||。
带回来五个，画 |||||。

这种方法简单粗暴，叫做"一维计数法" 。每一个符号（竖线）的权重都是一样的，都代表"1"。

但问题来了：如果今天部落大丰收，带回来 1000 个苹果，难道你要在墙上画 1000 条线吗？等你画完，手断了，墙也没地方了，最关键的是，当你想过来查账验证的时候，还没等你数完，数到第 382 个时候你估计就头晕眼花了，还得从头数起。

痛点总结： 所以单一符号无法高效表达大数值。

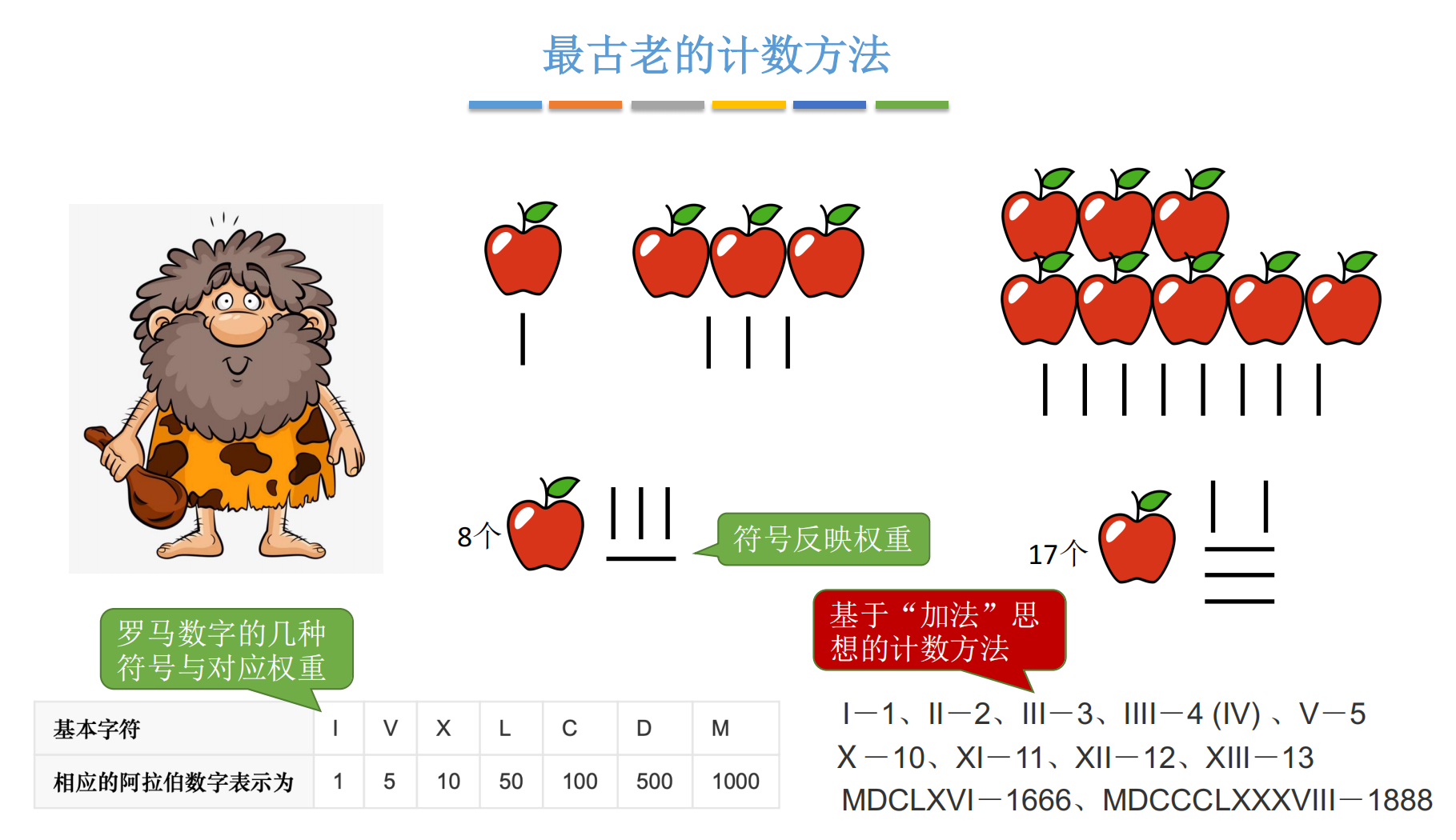
1.2 罗马数字：符号权重的诞生

为了解决这个问题，古人开始动脑子了："我们能不能用不同的符号，代表不同数量的苹果？"

于是，罗马数字诞生了。

I 代表 1。
V 代表 5。
X 代表 10。
L 代表 50，C 代表 100，D 代表 500，M 代表 1000。

这时候，如果你想记录 8 个苹果，不用画 8 条线，而是写成 VIII（这个本质上其实就是加法，这个就是5 + 1 + 1 + 1）。

如果你想记录 13 个苹果，写成 XIII。

这里出现了一个伟大的进步： 符号有了**权重（Weight）的概念。V 的权重是 5，I 的权重是 1。把它们加起来，就是数值。

但是，罗马数字依然有巨大的缺陷。想象一下，你要算"一万"怎么办？可能得发明个新符号叫 W。要算"十万"呢？再发明个 Y。随着数字越来越大，我们需要记忆的符号无穷无尽。

更要命的是，试着用罗马数字做个乘法？

MCMXCVI * XLII = ？

这简直是反人类！

1.3 阿拉伯数字与"位权"的魔法

真正拯救人类数学的，是古印度人，他们发明了阿拉伯数字（没错，阿拉伯数字是古印度人发明的，阿拉伯人只是做了一回"快递员"，把这个带入了欧洲）。

他们引入了两个核武器级别的概念：

有限的符号：只有 0, 1, 2, ... 9 这十个符号。
位置决定权重（位权）：同一个符号，放在不同的位置，代表的大小完全不同！

比如数字 975：

5 在个位，权重是 100=110^0=1100=1，它代表 5×15 \times 15×1。
7 在十位，权重是 101=1010^1=10101=10，它代表 7×107 \times 107×10。
9 在百位，权重是 102=10010^2=100102=100，它代表 9×1009 \times 1009×100。

这就是进位计数制的精髓。我们不需要为"一万"发明新符号，只需要把 1 写在万位上（10000）即可。

1.4 为什么人类选择了十进制？

这是一个有趣的生物学巧合。

你在教小孩子数数的时候，是不是下意识地伸出手指？

"1，2，3... 10"。哎呀，手指用完了！怎么办？

这时候，我们在地上放一块石头代表"一个十"，然后手指收回去，从头开始数。

这就是**"逢十进一"**。

因为人类有 10 根手指，所以十进制成了最符合人类直觉的计数系统。

所以如果《海绵宝宝》里的派大星要发明数学，它会用几进制？

海绵宝宝和派大星每只手只有 4 根手指，两只手加起来是 8 根。

所以，比基尼海滩的通用数学应该是八进制（Octal）！

在他们的世界里，数到 7 之后，下一个数就是 10（代表十进制的 8）。

1.5 R 进制系统

人类喜欢十进制，但计算机不喜欢。计算机由亿万个晶体管组成，对于一个电子元器件来说，维持 10 种不同的稳定电压状态（代表 0-9）太难了，很容易受干扰。

但是，区分**"通电"和"断电"**（高电平/低电平）却非常容易且稳定。

通电 = 1
断电 = 0

这就注定了计算机只能生活在二进制的世界里，

所以我们可以将十进制的逻辑推广到任意进制（R进制）。每一个数码位所用到的不同的符号的个数，就是所谓的基数。比如说十进制，在每个数码位有可能用到的符号会有012一直到9，总共有十种符号。那对于一个r进制的数来说，它的奇数就应该是r，也就是有可能会出现r种不一样的符号。

核心概念：

基数（Radix，记作 r）：每个数码位上能使用的不同符号的个数。
- 十进制 r=10（符号 0~9）
- 二进制 r=2（符号 0, 1）
- 八进制 r=8（符号 0~7）
- 十六进制 r=16（符号 0~9, A~F）
位权（Weight） ：第 iii 位的权重是 rir^iri。

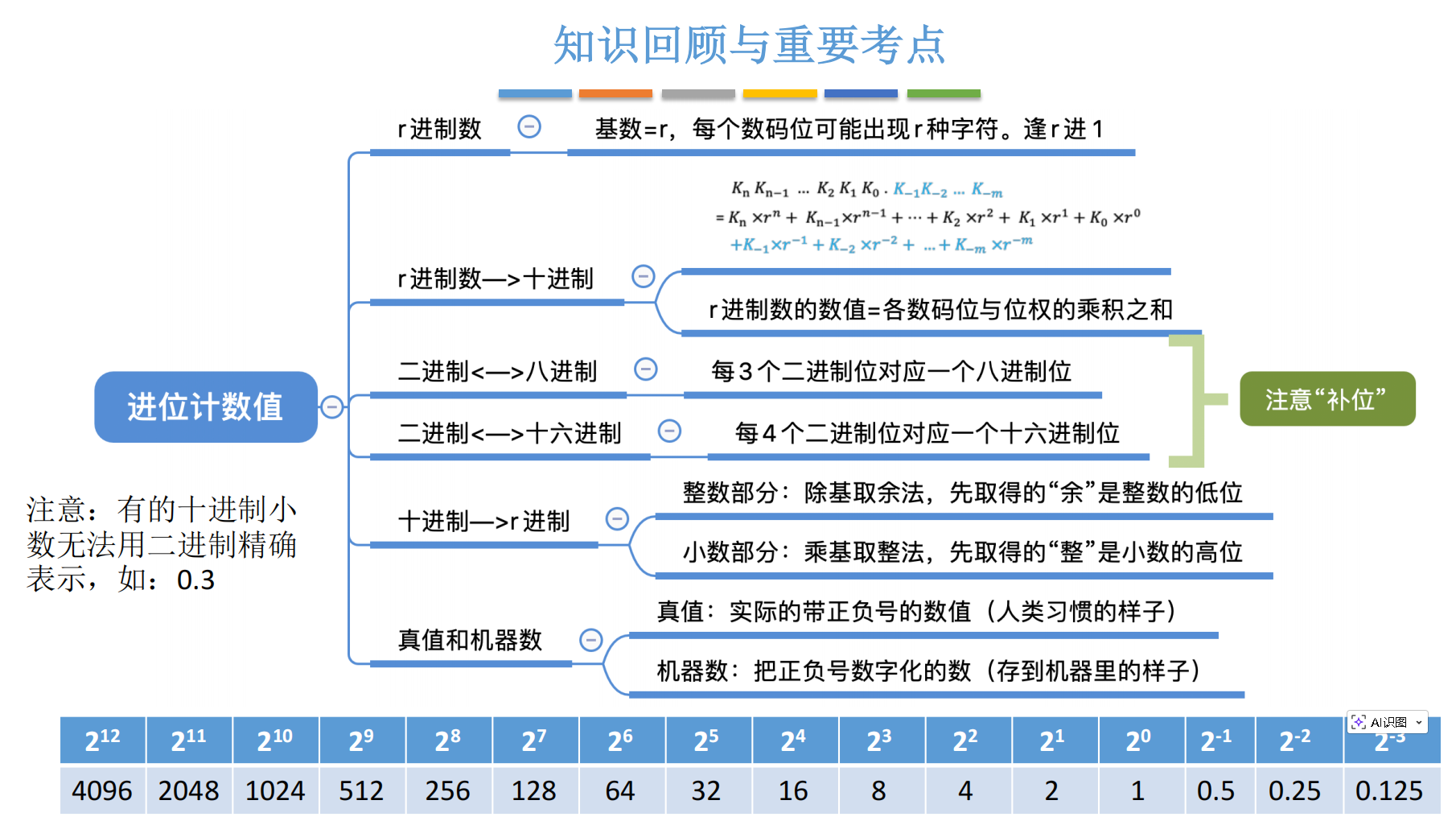
任意进制转十进制的通用公式（数值展开）：

(KnKn−1...K1K0.K−1K−2...)r=∑Ki×ri(K_n K_{n-1} ... K_1 K_0 . K_{-1} K_{-2} ...)_r = \sum K_i \times r^i(KnKn−1...K1K0.K−1K−2...)r=∑Ki×ri

其中：

KiK_iKi 是第 iii 位的系数（具体的数字）。
rir^iri 是第 iii 位的权。

1.6 各种进制的常⻅书写⽅式

后缀表示法：

二进制：1010B（Binary）
十六进制：1652H 或 0x1652
十进制：1652D（Decimal）

特殊前缀：0x为十六进制专用前缀

识别要点：

字母后缀具有最高优先级
无标注时需结合上下文判断

二、任意进制 →\rightarrow→ 十进制（按权展开法）

按权展开法是最简单的一种转换，只要你会做乘法和加法就能搞定。核心思想就是：把每一位上的数字，乘以它对应的权重，然后全部加起来。

2.1 二进制转十进制

【例题】 将二进制数 1101.1 转换为十进制。

解析：

我们先把每一位的"身份"列出来：

整数部分：
- 第 0 位（个位）：是 1，权重 20=12^0 = 120=1
- 第 1 位：是 0，权重 21=22^1 = 221=2
- 第 2 位：是 1，权重 22=42^2 = 422=4
- 第 3 位：是 1，权重 23=82^3 = 823=8
小数部分：
- 第 -1 位：是 1，权重 2−1=0.52^{-1} = 0.52−1=0.5

计算过程：

Value=1×23+1×22+0×21+1×20+1×2−1Value = 1 \times 2^3 + 1 \times 2^2 + 0 \times 2^1 + 1 \times 2^0 + 1 \times 2^{-1}Value=1×23+1×22+0×21+1×20+1×2−1

=8+4+0+1+0.5= 8 + 4 + 0 + 1 + 0.5=8+4+0+1+0.5

=13.5= 13.5=13.5

快速心算技巧：

对于以下常见数据，应该做到熟记于心，尽量看一下就明白其的转化关系：

20=12^0 = 120=1
21=22^1 = 221=2
22=42^2 = 422=4
23=82^3 = 823=8
24=162^4 = 1624=16
25=322^5 = 3225=32
26=642^6 = 6426=64
27=1282^7 = 12827=128
28=2562^8 = 25628=256 (一个字节的最大值)
210=10242^{10} = 1024210=1024 (1K)

看到 1101，你脑子里应该直接反应：8 + 4 + 1 = 13。不要再去写公式了，那是小学生的做法。

2.2 八进制转十进制

【例题】 将八进制数 5.4 转换为十进制。

解析：

5 在个位，权重 80=18^0 = 180=1。
4 在小数位，权重 8−1=1/8=0.1258^{-1} = 1/8 = 0.1258−1=1/8=0.125。

计算：

Value=5×1+4×0.125=5+0.5=5.5Value = 5 \times 1 + 4 \times 0.125 = 5 + 0.5 = 5.5Value=5×1+4×0.125=5+0.5=5.5

这里有个有趣的现象：八进制的 0.4 竟然等于十进制的 0.5！这也是为什么我们需要进制转换，因为直觉往往会骗人。

2.3 十六进制转十进制

十六进制（Hexadecimal）是程序员的浪漫。因为二进制写起来太长了（11111111），写成十六进制（FF）就简洁得多。

我们的阿拉伯数字符号只有九个，不够用来表示16个基数怎么办？我们使用字母来代替计算！

A = 10
B = 11
C = 12
D = 13
E = 14
F = 15

【例题】 将十六进制数 5.8 转换为十进制。

解析：

5 在个位，权重 160=116^0 = 1160=1。
8 在小数位，权重 16−1=1/16=0.062516^{-1} = 1/16 = 0.062516−1=1/16=0.0625。

计算：

Value=5×1+8×0.0625=5+0.5=5.5Value = 5 \times 1 + 8 \times 0.0625 = 5 + 0.5 = 5.5Value=5×1+8×0.0625=5+0.5=5.5

三、十进制 →\rightarrow→ 任意进制（最强算法）

如果想要把十进制数转化为任意进制数，就稍微麻烦一点点，但依旧很简单，我们有一个很简单的方法：

请记住口诀：整数除基取余，小数乘基取整。

3.1 整数转换：除基取余法（逆序）

原理：

假设我们要把十进制数 XXX 转为 rrr 进制。

X=knrn+...+k1r1+k0r0X = k_n r^n + ... + k_1 r^1 + k_0 r^0X=knrn+...+k1r1+k0r0

X=r×(knrn−1+...+k1)+k0X = r \times (k_n r^{n-1} + ... + k_1) + k_0X=r×(knrn−1+...+k1)+k0

你看，如果我们把 XXX 除以 rrr，商是括号里那一坨，而余数恰好就是 k0k_0k0（最低位）！

拿着商继续除以 rrr，得到的余数就是 k1k_1k1。

【例题】 将十进制 75 转换为二进制。

步骤（短除法）：

75÷2=3775 \div 2 = 3775÷2=37 ...... 余 1 (这是 K0K_0K0，最低位)
37÷2=1837 \div 2 = 1837÷2=18 ...... 余 1
18÷2=918 \div 2 = 918÷2=9 ...... 余 0
9÷2=49 \div 2 = 49÷2=4 ...... 余 1
4÷2=24 \div 2 = 24÷2=2 ...... 余 0
2÷2=12 \div 2 = 12÷2=1 ...... 余 0
1÷2=01 \div 2 = 01÷2=0 ...... 余 1 (这是最高位)

结果： 将余数**从下往上（从高位到低位）**书写：1001011。

3.2 小数转换：乘基取整法（顺序）

原理：

假设小数 Y=0.k−1r−1+k−2r−2+...Y = 0.k_{-1} r^{-1} + k_{-2} r^{-2} + ...Y=0.k−1r−1+k−2r−2+...

Y×r=k−1+(k−2r−1+...)Y \times r = k_{-1} + (k_{-2} r^{-1} + ...)Y×r=k−1+(k−2r−1+...)

你看，乘以 rrr 之后，整数部分恰好就是 k−1k_{-1}k−1（小数点后第一位），剩下的小数部分继续乘。

【例题】 将十进制 0.3 转换为二进制。

步骤：

0.3×2=0.60.3 \times 2 = 0.60.3×2=0.6 →\rightarrow→ 取整数 0 (这是 K−1K_{-1}K−1)
0.6×2=1.20.6 \times 2 = 1.20.6×2=1.2 →\rightarrow→ 取整数 1
(注意：取走整数1后，剩下0.2) 0.2×2=0.40.2 \times 2 = 0.40.2×2=0.4 →\rightarrow→ 取整数 0
0.4×2=0.80.4 \times 2 = 0.80.4×2=0.8 →\rightarrow→ 取整数 0
0.8×2=1.60.8 \times 2 = 1.60.8×2=1.6 →\rightarrow→ 取整数 1
(剩下0.6) 0.6×2=1.20.6 \times 2 = 1.20.6×2=1.2 →\rightarrow→ 取整数 1
... 死循环了！

你会发现，0.6 再次出现了！这意味计算进入了无限循环 00110011...。

结果： 将整数从上往下 书写：0.0100110011...

** 高能考点警告：**

当然，并不是所有的小数都能用二进制精确表示！

像 0.5 (2−12^{-1}2−1), 0.25 (2−22^{-2}2−2), 0.75 (0.5+0.250.5+0.250.5+0.25) 这种可以精确表示。

但像 0.3, 0.1 这种，在二进制里是无限循环小数。

这就是为什么你在 Java 或 Python 里计算 0.1 + 0.2，结果往往不是 0.3，而是 0.30000000000000004。这不是Bug，这是进制转换的数学特性导致的精度丢失（后续浮点数章节会详细讲）。

3.3 拼凑法（高手必备）

在考场上，画短除法太慢了。对于不太大的数，我们可以用"减法拼凑"的思想。

【例题】 将 260.75 转换为二进制。

整数部分 260：

找个最接近 260 的 2n2^n2n？是 256 (282^828)。
260−256=4260 - 256 = 4260−256=4。
找 4？就是 222^222。
所以 260=256+4260 = 256 + 4260=256+4。
在第 8 位和第 2 位填 1，其他填 0。
- 282^828 (第9位) -> 1
- ... 00000 ...
- 222^222 (第3位) -> 1
- 21,202^1, 2^021,20 -> 0
- 结果：100000100

小数部分 0.75：

0.75=0.5+0.250.75 = 0.5 + 0.250.75=0.5+0.25
0.5=2−10.5 = 2^{-1}0.5=2−1
0.25=2−20.25 = 2^{-2}0.25=2−2
结果：.11

总结果： 100000100.11

这种方法熟练后，速度比短除法快 3 倍以上！

四、二、八、十六进制的"特殊通道"

为什么程序员偏爱 8 进制和 16 进制？不仅仅因为它们短，更因为它们和二进制之间存在完美的对应关系。

八进制 (23=82^3=823=8) ：每 3 个二进制位，对应 1 个八进制位。
十六进制 (24=162^4=1624=16) ：每 4 个二进制位，对应 1 个十六进制位。

4.1 二进制 ↔\leftrightarrow↔ 八进制

转换规则： 以小数点为界，整数向左 每3位一组，小数向右 每3位一组。不足补0。

【例题】 二进制 11110.10 转八进制。

分组：

整数：11 110 →\rightarrow→ 补零变成 011 110
- 011 = 3
- 110 = 6
小数：.10 →\rightarrow→ 补零变成 .100
- 100 = 4

结果： 36.4 (八进制通常写作 36.4836.4_836.48 或 36.4O36.4O36.4O)

4.2 二进制 ↔\leftrightarrow↔ 十六进制

转换规则： 同理，4位一组。

【例题】 二进制 111100.101 转十六进制。

分组：

整数：11 1100 →\rightarrow→ 补零 0011 1100
- 0011 = 3
- 1100 = 12 (对应 C)
小数：.101 →\rightarrow→ 补零 .1010
- 1010 = 10 (对应 A)

结果： 3C.A (十六进制通常写作 0x3CA 或 3CAH)

🔧 常见误区提示：

补零的方向千万别搞反！

整数是在最左边补0（10变成010，值不变）。

小数是在最右边补0（0.1变成0.10，值不变）。

如果你在整数右边补0（10变成100），那就相当于乘以2了，大错特错！

五、真值与机器数

最后，我们来聊两个概念，为后面的章节做铺垫。

5.1 真值 (True Value)

就是我们人类书写的、带有正负号的数字。比如：+15, -8, +0.5。这是给人看的，符合人类习惯。

5.2 机器数 (Machine Number)

是数字在计算机里的实际存储形式。计算机里没有 + 和 - 号，怎么办？ 用 0 和 1 代替！

通常规定：0 代表正，1 代表负。
这一个表示符号的位，放在数字的最前面，叫做符号位。

比如真值 -5 (二进制 101)。如果不考虑复杂的编码（原反补），简单地把符号位加上去：

符号位 1 (负)
数值位 101
机器数可能长这样：1101

但实际上，计算机为了方便做减法运算，发明了原码、反码、补码、移码 。这些让人头大的概念，我们将在下一篇博客中详细拆解。

结语

文章的最后，给基础不好的同学，或者觉得枯燥的同学讲个好玩的事。

你知道吗？德国的大数学家莱布尼茨（微积分的发明者之一）被认为是现代二进制的发明者。但当他看到中国的《易经》八卦图时，震惊得下巴都掉了。

太极生两仪：阴（--）和阳（---）。这不就是 0 和 1 吗？
两仪生四象：太阴、少阳、少阴、太阳。这不就是 00, 01, 10, 11 吗？
四象生八卦：乾、坤、震、巽... 每一卦由三根爻组成。
- 坤卦（全是阴爻）：000 (0)
- 乾卦（全是阳爻）：111 (7)

所以，咱们的老祖宗早在几千年前，就已经悟出了二进制的真谛。不管是算命先生掐指一算，还是程序员敲击键盘，本质上，我们都在玩弄 0 和 1 的艺术。