环形子数组的最大和

题目

给定一个长度为 n 的环形整数数组 nums ，返回 nums 的非空子数组的最大可能和。

环形数组意味着数组的末端将会与开头相连呈环状。形式上， nums[i] 的下一个元素是 nums[(i + 1) % n] ， nums[i] 的前一个元素是 nums[(i - 1 + n) % n] 。

子数组最多只能包含固定缓冲区 nums 中的每个元素一次。形式上，对于子数组 nums[i], nums[i + 1], ..., nums[j] ，不存在 i <= k1, k2 <= j 其中 k1 % n == k2 % n 。

示例 1：

输入：nums = [1,-2,3,-2]

输出：3

解释：从子数组 [3] 得到最大和 3

示例 2：

输入：nums = [5,-3,5]

输出：10

解释：从子数组 [5,5] 得到最大和 5 + 5 = 10

示例 3：

输入：nums = [3,-2,2,-3]

输出：3

解释：从子数组 [3] 和 [3,-2,2] 都可以得到最大和 3

提示：

n == nums.length

1 <= n <= 3 * 104

-3 * 104 <= nums[i] <= 3 * 104

代码

方法一：动态规划

思路与算法

求解普通数组的最大子数组和是求解环形数组的最大子数组和问题的子集。设数组长度为 n，下标从 0 开始，在环形情况中，答案可能包括以下两种情况：

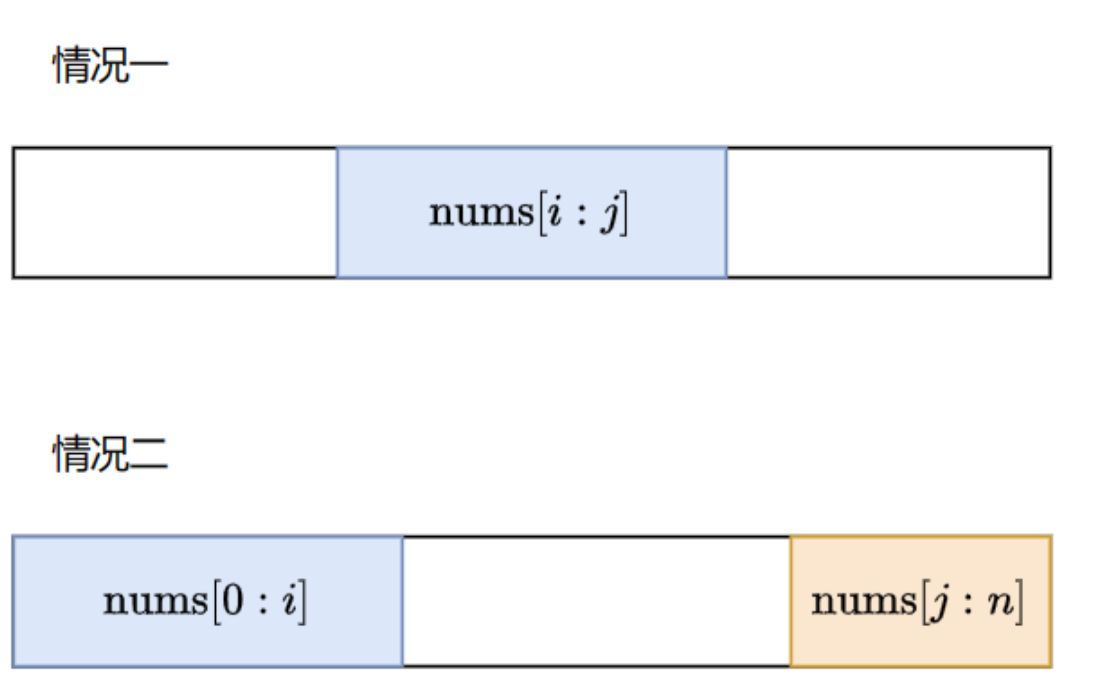
构成最大子数组和的子数组为 nums[i:j]，包括 nums[i] 到 nums[j−1] 共 j−i 个元素，其中 0≤i<j≤n。

构成最大子数组和的子数组为 nums[0:i] 和 nums[j:n]，其中 0<i<j<n。

第一种情况的求解方法与求解普通数组的最大子数组和方法完全相同。

第二种情况中，答案可以分为两部分，nums[0:i] 为数组的某一前缀，nums[j:n] 为数组的某一后缀。求解时，我们可以枚举 j，固定 sum(nums[j:n]) 的值，然后找到右端点坐标范围在 [0,j−1] 的最大前缀和，将它们相加更新答案。

右端点坐标范围在 [0,i] 的最大前缀和可以用 leftMax[i] 表示，递推方程为：leftMax[i]=max(leftMax[i−1],sum(nums[0:i+1])

至此，我们可以使用以上方法求解出环形数组的最大子数组和。

java 复制代码

class Solution {
    public int maxSubarraySumCircular(int[] nums) {
        int n = nums.length;
        int[] leftMax = new int[n];
        // 对坐标为 0 处的元素单独处理，避免考虑子数组为空的情况
        leftMax[0] = nums[0];
        int leftSum = nums[0];
        int pre = nums[0];
        int res = nums[0];
        for (int i = 1; i < n; i++) {
            pre = Math.max(pre + nums[i], nums[i]);
            res = Math.max(res, pre);
            leftSum += nums[i];
            leftMax[i] = Math.max(leftMax[i - 1], leftSum);
        }

        // 从右到左枚举后缀，固定后缀，选择最大前缀
        int rightSum = 0;
        for (int i = n - 1; i > 0; i--) {
            rightSum += nums[i];
            res = Math.max(res, rightSum + leftMax[i - 1]);
        }
        return res;
    }
}

时间复杂度： O(n)，其中 n 是 nums 的长度。求解第一种情况的时间复杂度为 O(n)，求解 leftMax 数组和枚举后缀的时间复杂度为 O(n)，因此总的时间复杂度为 O(n)。

空间复杂度： O(n)，其中 n 是 nums 的长度。过程中我们使用 leftMax 来存放最大前缀和。

方法二：取反

思路与算法

对于第二种情况，即环形数组的最大子数组和为 nums[0:i] 和 nums[j:n]，我们可以找到普通数组最小的子数组 nums[i:j] 即可。而求解普通数组最小子数组和的方法与求解最大子数组和的方法完全相同。

令 maxRes 是普通数组的最大子数组和，minRes 是普通数组的最小子数组和，我们可以将 maxRes 与 ∑i=0nnums[i]−minRes 取最大作为答案。

需要注意的是，如果 maxRes<0，数组中不包含大于等于 0 的元素，minRes 将包括数组中的所有元素，导致我们实际取到的子数组为空。在这种情况下，我们只能取 maxRes 作为答案。

typescript 复制代码

class Solution {
    public int maxSubarraySumCircular(int[] nums) {
        int n = nums.length;
        int preMax = nums[0], maxRes = nums[0];
        int preMin = nums[0], minRes = nums[0];
        int sum = nums[0];
        for (int i = 1; i < n; i++) {
            preMax = Math.max(preMax + nums[i], nums[i]);
            maxRes = Math.max(maxRes, preMax);
            preMin = Math.min(preMin + nums[i], nums[i]);
            minRes = Math.min(minRes, preMin);
            sum += nums[i];
        }
        if (maxRes < 0) {
            return maxRes;
        } else {
            return Math.max(maxRes, sum - minRes);
        }
    }
}

时间复杂度： O(n)，其中 n 是 nums 的长度。我们遍历 2n 个元素，每个元素最多入队出队一次，因此总的时间复杂度为 O(n)。

空间复杂度： O(n)，其中 n 是 nums 的长度。