一、思路:
(1)本题和684.冗余连接类似,但本题是一个有向图,相对要复杂一些。
(2)题目要求:有一个有向图,是由一棵有向树 + 一条有向边组成的(所以此时这个图就不能称之为有向树),现在要求找到这条有向边并将其删除,使得这个图可以恢复为有向树。
(3)若有多条可以删除的边,则删除顺序靠后的边。
(4)有向树的性质:对于一棵有向树,只有根节点的入度为0,其他节点的入度都为1(因为该树除了根节点之外的每一个节点都有且只有一个父节点,而根节点没有父节点)。
二、分情况讨论:
1.情况一:找到入度为2的节点,则直接删除一条指向该节点的边即可。
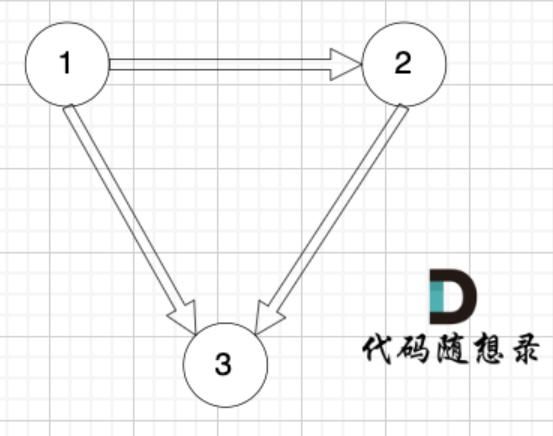
如下图所示:
找到了节点3的入度为2,删1->3或者2->3,选择删顺序靠后的便可。
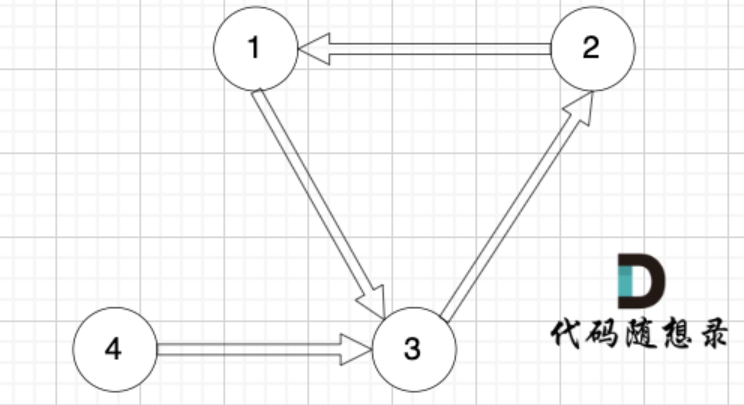
2.情况二:入度为2的节点还有一种情况,如下图所示:
节点3的入度为2,但在删除边的时候,由于存在有向环,只能删这条边(节点1->节点3),如果删除边(节点4->节点3),那么删除后本图也不是有向树了,因为找不到根节点。
综上所述,如果遇到入度为2的节点,需要判断删哪一条边,删除后能使本图成为有向树。如果是删哪个都可以,优先删顺序靠后的边。
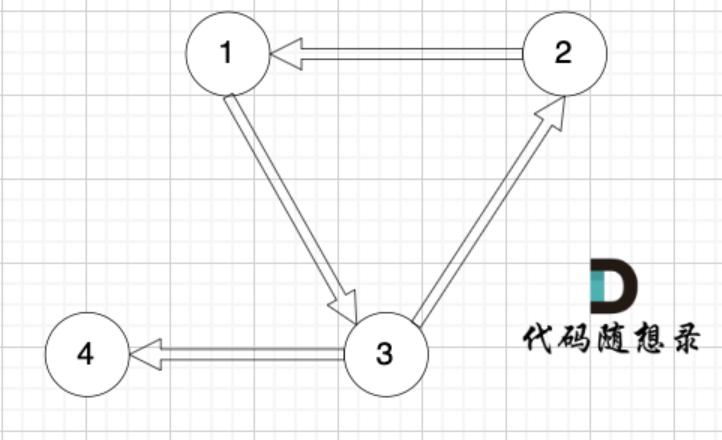
3.情况三:如果没有入度为2的点,说明图中有环(注意是有向环)且添加的边指向了根节点,如下图所示:
此时删掉构成环的边即可。
三、解决方法。
1.首先计算每个节点的入度,如果存在入度为2的节点,就定位到该节点对应的两条边,分别记为dup[0]和dup[1]。如果在删除dup[1]后,剩余的边无法形成树,说明dup[0]是需要删除的边;否则说明dup[1]是需要删除的边。
2.如果不存在入度为2的节点,就遍历数组edges,对于每条边(u,v),使用并查集维护节点之间的连通性。如果u和v已经连通,说明图中存在有向环,此时当前边即为需要删除的边。
附代码:
java
class Solution {
int[] parent;
int find(int x) {
if (parent[x] != x) parent[x] = find(parent[x]);
return parent[x];
}
void union(int x, int y) {
if (find(x) != find(y)) parent[find(y)] = parent[x];
}
public int[] findRedundantDirectedConnection(int[][] edges) {
parent = new int[1001];
int[] in = new int[1001]; //记录每个节点的入度
int[] res = {}; //存储可能的多余边
// 寻找是否存在入度为 2 的顶点
for (int[] e : edges) {
if (++in[e[1]] == 2) { //如果某个节点的入度变为2
res = e; //记录最后一条使入度变为2的边
}
}
// 如果存在入度为 2 的顶点
// 尝试删除指向该顶点的某一条边,看剩下的点是否能够构成树
// 如果可以构成树,直接返回该边,否则返回另一条边
if (res.length != 0) {
if (check(edges, res)) return res; //如果删除res边后能成树,则返回res
else {
//否则返回另一条指向同一个节点的边
for (int[] e : edges) if (e[1] == res[1]) return e;
}
}
// 重新初始化并查集
for (int i = 0; i < 1001; i++) {
parent[i] = i;
}
for (int[] e : edges) {
//如果两个节点已经在同一个集合,说明这条边会成环
// 删除加入形成环的边
if (find(e[0]) == find(e[1])) return e;
else union(e[0], e[1]);
}
return new int[0];
}
// 判断有向边构成的图形是否为树
boolean check(int[][] edges, int[] remove) {
// 初始化并查集
for (int i = 0; i < 1001; i++) {
parent[i] = i;
}
for (int[] e : edges) {
// 跳过要删除的边
if (Arrays.equals(e, remove)) continue;
// 如果删除后还有环,说明删除的不是正确的边
if (find(e[0]) == find(e[1])) return false;
else union(e[0], e[1]);
}
return true;
}
}