【算法基础篇】（三十四）图论基础深度解析：从概念到代码，玩转图的存储与遍历

前言

在数据结构的世界里，线性表是简单的 "排队"，树是层次分明的 "家族树"，而图则是打破所有束缚的 "社交网络"------ 任意两个节点都能自由建立连接，复杂却又充满规律。作为算法面试和工程实践的核心基础，图论的重要性无需多言。今天这篇文章，我们就从最底层的概念入手，结合生动案例和可直接运行的 C++ 代码，手把手带你吃透图的基本概念、存储方式与遍历算法，让你从 "图盲" 变身 "图论入门高手"！下面就让我们正式开始吧！

一、图的基本概念：搞懂这些，才算真正入门

在正式敲代码之前，我们必须先理清图论的核心概念。很多人觉得图论抽象，其实只要把 "顶点" 看作 "人"，"边" 看作 "人与人之间的关系"，一切都会变得通俗易懂。

1.1 图的定义：不止是 "点" 和 "线" 的组合

从学术角度来说，图（Graph）是由顶点集（V） 和边集（E） 组成的二元组，记为 G = (V, E)。其中：

顶点集 V 是有限非空集合，每个元素称为顶点（Vertex），可以理解为 "社交网络里的人"；

边集 E 是顶点之间关系的集合，每条边（Edge）连接两个顶点，对应 "人与人之间的朋友关系"。

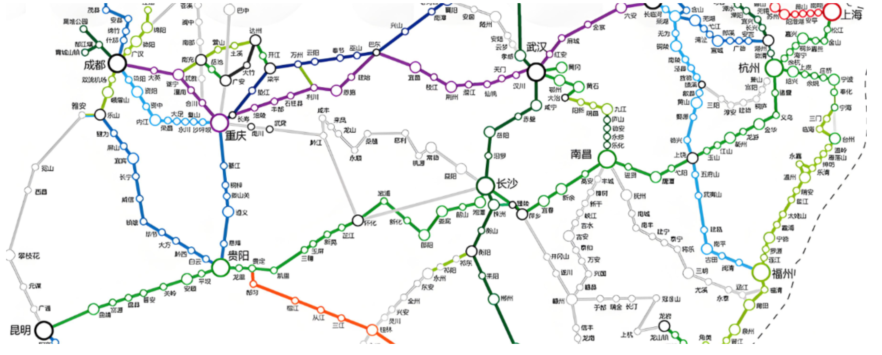
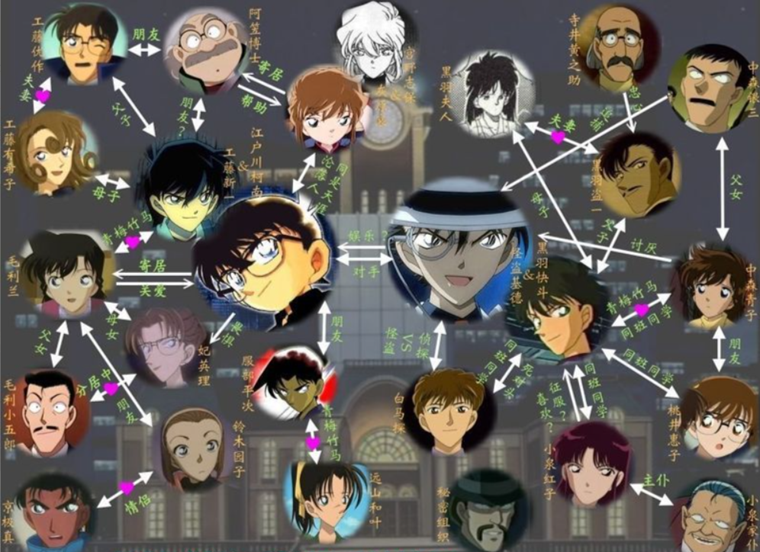
我们用**|V|表示顶点个数** （也称图的 "阶" ），用**|E|表示边的条数**。举个例子：微信好友网络中，每个用户是顶点，两个用户之间的好友关系就是一条边，整个微信好友网络就是一个庞大的图。

这里必须强调图与线性表、树的核心区别：

线性表：元素间是 "一对一" 关系（除首尾元素外，每个元素只有一个前驱和一个后继），比如排队买奶茶的队伍；

树：元素间是 "一对多" 关系（每个元素有唯一双亲，可有多个子节点），比如公司的组织架构图；

图：元素间是 "多对多" 关系（任意两个顶点都可能相连），比如城市交通网络、社交关系网。

正是这种 "多对多" 的灵活性，让图成为描述复杂关系的最佳数据结构。

1.2 有向图和无向图：关系是 "双向奔赴" 还是 "单向暗恋"

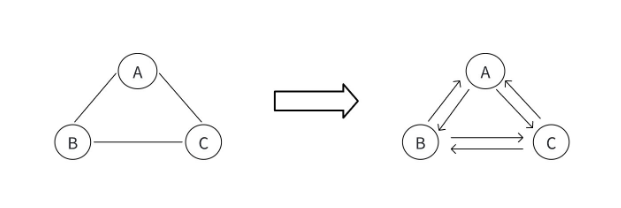
根据边是否有方向，图可以分为无向图和有向图，这是图论中最基础的分类。

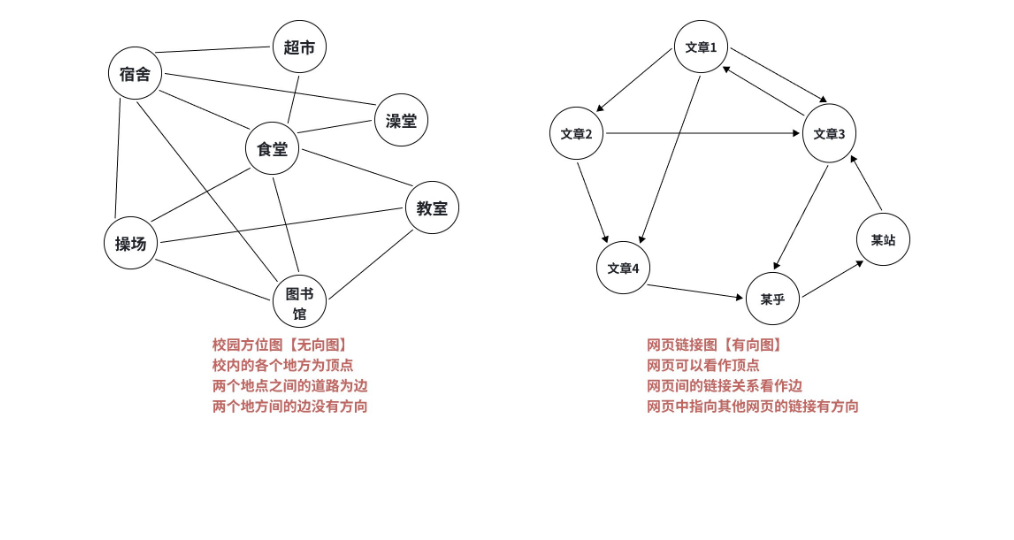
无向图：双向可达的 "对等关系"

无向图中的边没有方向，连接顶点 u 和 v 的边可以表示为**(u, v)，且(u, v) = (v, u)**。比如：

城市道路中，双向车道就是无向边（从 A 市到 B 市和从 B 市到 A 市走的是同一条路）；

微信好友关系也是无向边（你加了别人好友，别人也自动成为你的好友）。

文档中的 "校园方位图" 就是典型的无向图：宿舍、食堂、图书馆等地点是顶点，连接这些地点的道路是无向边，你可以从宿舍走到食堂，也能从食堂走回宿舍。

有向图：单向通行的 "依赖关系"

有向图中的边有明确方向，连接顶点 u 和 v 的边表示为**<u, v>**，表示从 u 指向 v，且 <u, v> ≠ <v, u>。比如：

城市道路中的单行线（只能从 A 路开往 B 路，不能反向）；

网页链接（从网页 A 点击链接跳转到网页 B，不代表能从 B 跳回 A）；

课程学习依赖（必须先学《高等数学》才能学《线性代数》，这就是一条从 "高数" 指向 "线代" 的有向边）。

文档中的 "网页链接图" 就是有向图：每个网页是顶点，链接是有向边，方向由 "当前网页" 指向 "目标网页"。

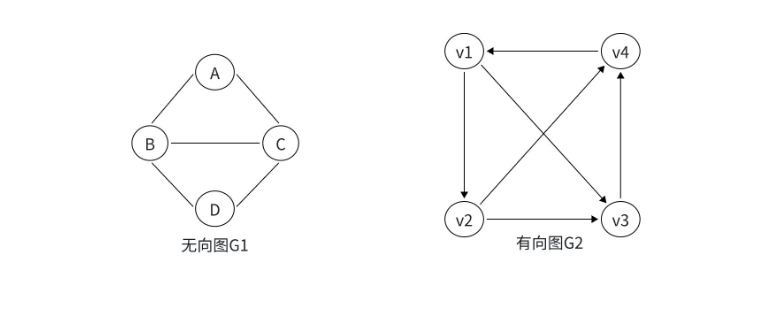
这里有个实用技巧：在算法实现中，我们可以把无向边看作两条方向相反的有向边（比如无向边 (u, v) 等价于有向边 <u, v> 和 <v, u>），这样就能统一用有向图的逻辑处理所有图，简化代码实现。

1.3 简单图与多重图：关系是否 "唯一"

现实中，两个人可能有多种联系方式（微信、电话、短信），对应到图中，就有了简单图和多重图的区别。

关键定义：

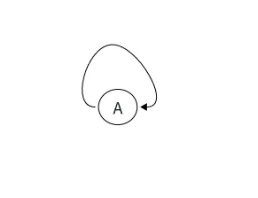
自环：顶点自己指向自己的边（比如一个网页有指向自身的链接）；

重边：两个顶点之间存在两条或以上完全相同的边（比如从 A 市到 B 市有两条不同的高速公路）。

分类：

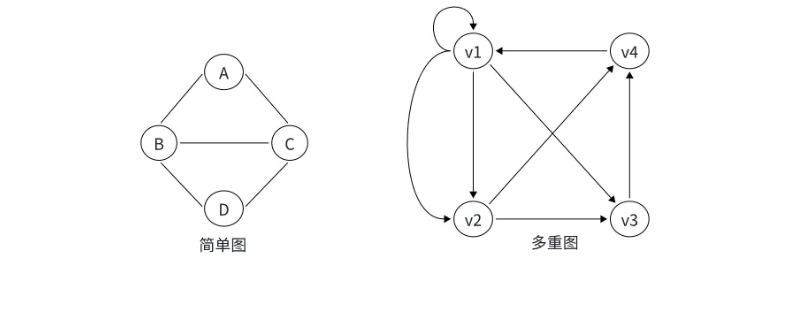
简单图：没有自环和重边的图（大部分算法问题默认是简单图）；

多重图：存在自环或重边的图（比如交通网络中，A 和 B 之间可能有普通公路和高铁两条边）。

下图分别为自环和重边：

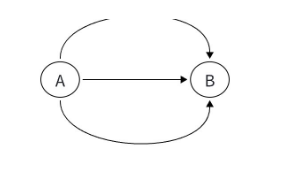
比如：社交网络中，你和朋友之间只有 "好友" 这一种关系，对应简单图；而城市交通网络中，A 和 B 之间可能有公交、地铁、自驾三条路径，对应多重图。

1.4 稠密图和稀疏图：关系是 "密集" 还是 "稀疏"

根据边的条数多少，图可以分为稠密图和稀疏图，这直接决定了我们选择哪种存储方式（后面会详细说）。

稀疏图：边的条数很少，满足 E < N log₂N（N 是顶点数）。比如：全国城市交通网（顶点是城市，边是高速公路，城市多但高速公路相对少）；

稠密图：边的条数很多，接近顶点数的平方（N²）。比如：完全图（任意两个顶点之间都有边），比如一个班级的同学之间，每个人都和其他人是好友，就是稠密图。

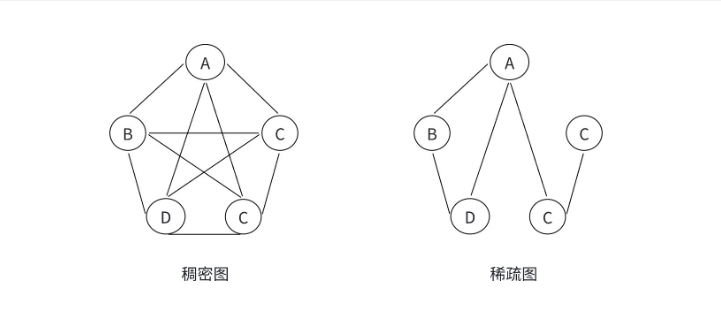
记住这个判断标准：稀疏图用**"邻接表"** 存储更高效，稠密图用**"邻接矩阵"** 存储更方便。后续我会详细为大家介绍。

1.5 顶点的度：每个 "人" 有多少 "关系"

顶点的度（Degree） 是衡量顶点 "活跃度" 的指标，定义为与该顶点相关联的边的条数，记为 deg (v)。根据图的有向 / 无向，度又分为入度和出度。

无向图中的度：

无向图中，顶点的度 = 入度（indeg）= 出度（outdeg）。因为边没有方向，不存在 "进来" 和 "出去" 的区别。

比如：无向图中，顶点 B 连接了 A、C、D 三条边，那么 deg (B) = indeg (B) = outdeg (B) = 3。

这里有个重要性质：无向图中所有顶点的度之和 = 2 × 边数。因为每条边会给两个顶点各贡献 1 个度，比如边 (u, v) 会让 u 的度 + 1，v 的度 + 1，总度之和增加 2。

有向图中的度：

有向图中，边有方向，因此度分为：

入度（indeg (v)）：以 v 为终点的有向边的条数（比如有多少人主动加你好友）；

出度（outdeg (v)）：以 v 为起点的有向边的条数（比如你主动加了多少人好友）；

总度 deg (v) = 入度 + 出度。

比如：有向图中，顶点 v1 有 1 条入边（别人指向它）和 2 条出边（它指向别人），那么 indeg (v1)=1，outdeg (v1)=2，deg (v1)=3。

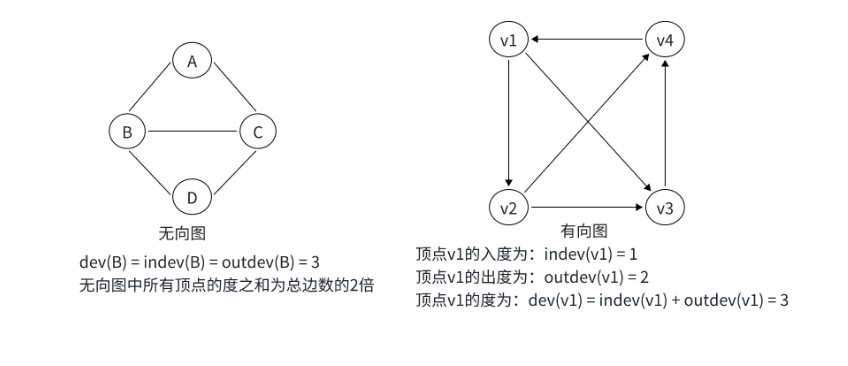
1.6 路径：从 "起点" 到 "终点" 的路线

在图中，路径是从一个顶点到另一个顶点的顶点序列。比如：从宿舍到图书馆，经过 "宿舍→食堂→教学楼→图书馆"，这个序列就是一条路径。

定义：在图 G=(V, E) 中，从顶点 vi 出发，沿若干边经过顶点 vp1, vp2, ..., vpm，到达顶点 vj，那么顶点序列 (vi, vp1, vp2, ..., vpm, vj) 就是从 vi 到 vj 的路径。

关键注意点：两个顶点之间的路径可能不唯一。比如从宿舍到图书馆，还可以走 "宿舍→操场→图书馆"，这就是另一条路径。算法中很多问题（比如最短路），本质就是找两条顶点之间 "最优" 的路径。

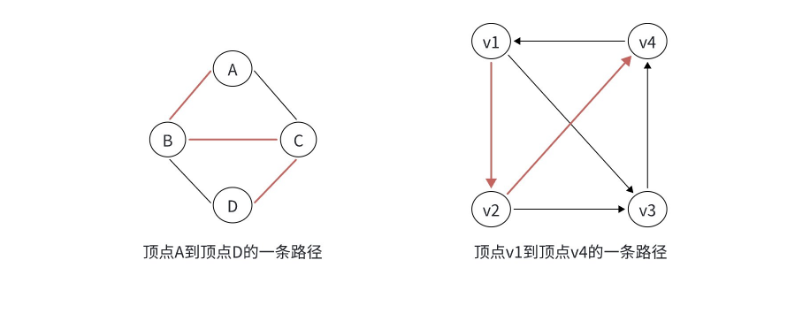
1.7 简单路径与回路：路线是否 "重复"、是否 "闭环"

路径有 "简单" 和 "非简单" 之分，而回路则是一种特殊的路径。

简单路径：路径上的所有顶点都不重复（比如 "宿舍→食堂→图书馆"，每个地点只经过一次）；

非简单路径：路径上有重复顶点（比如 "宿舍→食堂→宿舍→图书馆"，宿舍经过了两次）；

回路（环）：路径的起点和终点相同，且其他顶点不重复（比如 "宿舍→食堂→教学楼→宿舍"，形成一个闭环）。

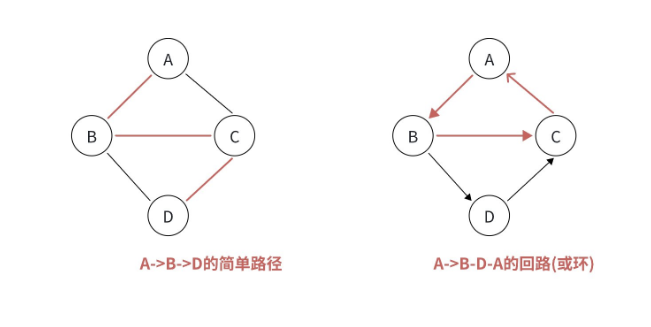
回路是很多算法问题的关键：比如判断图是否有环（拓扑排序的核心）、找图中的最小环（Floyd 算法的应用）等。

1.8 路径长度和带权路径长度：路线的 "距离" 或 "成本"

路径长度不是指物理距离，而是路径的 "代价"，分为两种情况：

不带权图：

路径长度 = 路径上的边的条数。比如 "宿舍→食堂→图书馆" 有 2 条边，路径长度就是 2。

带权图（网络）：

有些图的边会附带一个数值（称为 "权值"），用来表示距离、时间、成本等。这种图称为 "网络"（比如交通网中，边的权值是城市间的距离；物流网中，边的权值是运输成本）。

带权路径长度 = 路径上所有边的权值之和。比如：从 A 到 B 的边权值是 5，从 B 到 C 的边权值是 3，那么路径 "A→B→C" 的长度是 5+3=8。

举个例子：下面的工程施工周期图"就是带权图，边的权值是施工天数，路径长度就是完成该路径对应施工步骤所需的总时间。

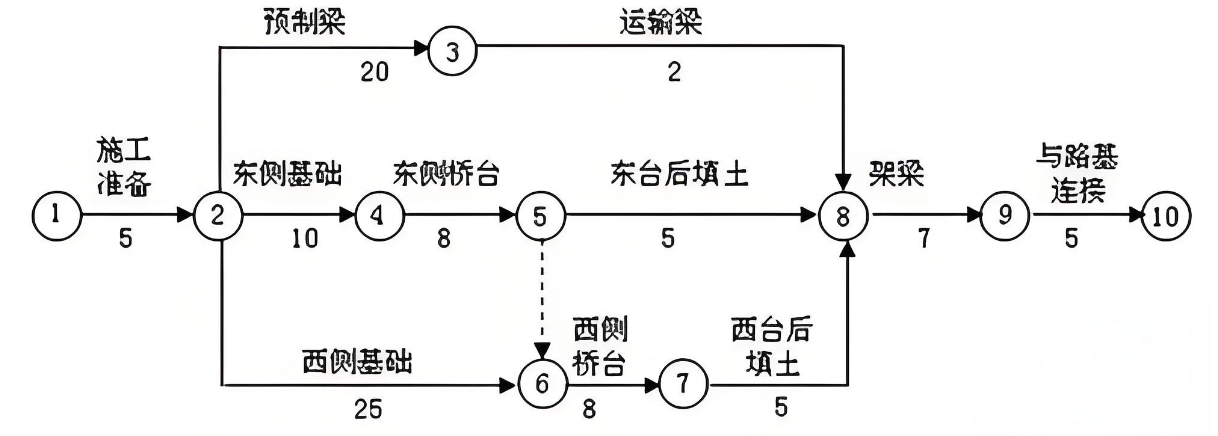
1.9 子图：从 "大网络" 中提取 "小网络"

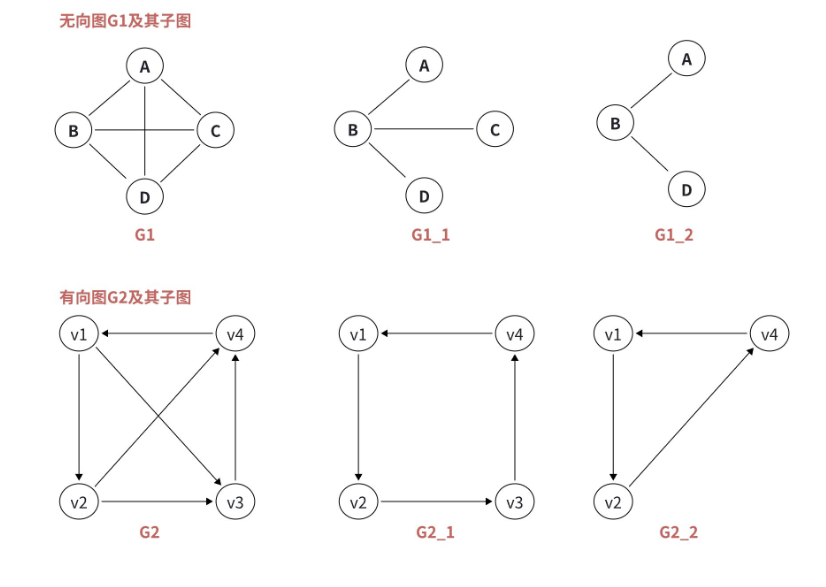
子图就像从一个庞大的社交网络中，提取出 "大学同学" 这个小圈子 ------ 包含原网络的部分顶点和部分边，且这些顶点和边能构成一个合法的图。

定义：设图 G=(V, E) 和图 G'=(V', E')，如果 V' ⊆ V 且 E' ⊆ E，那么 G' 是 G 的子图。

特殊情况：

生成子图 ：V' = V（包含原图所有顶点），但E' ⊆ E（只包含部分边）。比如：从全国交通网中，只保留高速公路，顶点还是所有城市，这就是生成子图。

简单说：子图可以 "少点少边"，生成子图只能 "少边不能少点"。

1.10 连通图与连通分量："网络" 是否 "互通"

在无向图中，"连通" 是指两个顶点之间有路径可达；而在有向图中，这一概念更复杂（分为强连通、弱连通），这里先聚焦无向图的连通性。

关键定义：

连通：无向图中，若从顶点 v1 到 v2 有路径，则称 v1 和 v2 是连通的；

连通图：无向图中，任意两个顶点都是连通的（比如一个班级的同学，任意两个人之间都有好友路径）；

非连通图：存在至少一对顶点不连通（比如两个独立的班级，班级内互通，但班级间没有好友关系）；

连通分量：无向图中的 "极大连通子图"（包含尽可能多的顶点和边，且是连通的）。非连通图可以分解为多个连通分量。

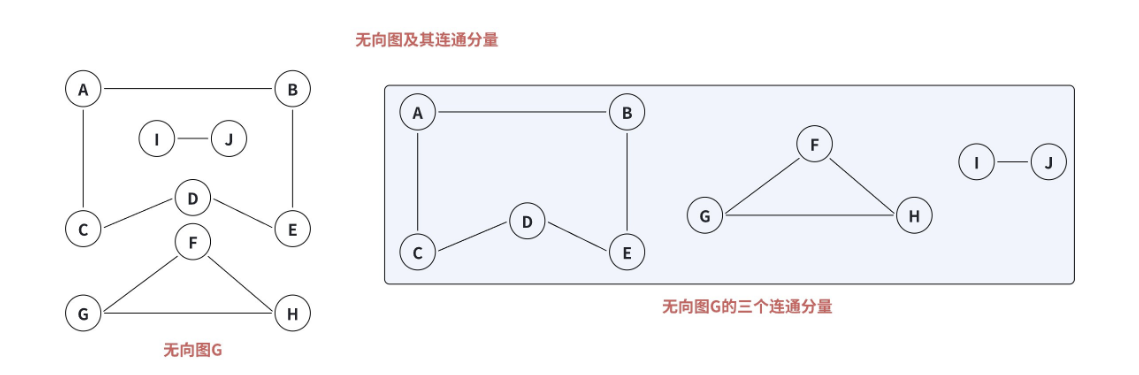
比如：全国交通网中，如果西藏的某个县城没有公路连接其他地区，那么全国交通网就是非连通图，该县城是一个连通分量，其他地区是另一个连通分量。

重要性质：n 个顶点的连通图，边数至少为 n-1（比如树就是边数最少的连通图）；如果边数 < n-1，那么图一定是非连通的。

1.11 生成树：连通图的 "最小骨架"

生成树是连通图的核心结构，也是很多算法（比如最小生成树）的基础。

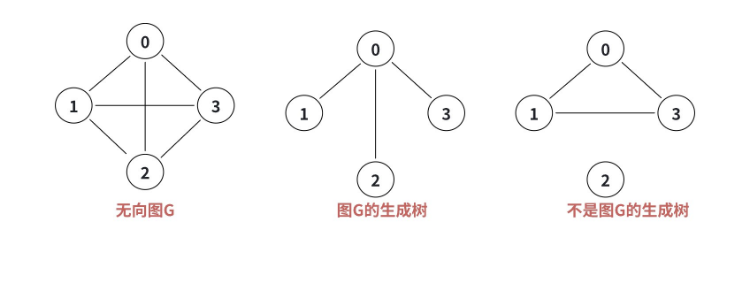
定义：连通图的生成树是包含所有顶点的**"极小连通子图"**------"极小" 意味着：

边数 = n-1（n 是顶点数）；

砍去任意一条边，图就变成非连通；

增加任意一条边，图就会形成回路。

比如：全国交通网的生成树，就是保留所有城市，且用最少的公路连接所有城市（去掉多余的公路），此时任意两个城市之间只有一条路径，砍去任意一条公路都会导致某个城市孤立。

生成树的特点：

连通性：生成树是连通的；

无环性：生成树中没有回路；

最小性：边数最少（n-1 条）。

一个连通图可以有多个生成树，比如 3 个顶点的完全图（边数 3），生成树有 3 种（每种生成树包含 2 条边）。

二、图的存储：如何用代码 "记录" 图的结构

搞懂了图的基本概念，接下来就是核心问题：如何在计算机中存储图？选择合适的存储方式，直接影响算法的效率。常用的存储方式有三种：邻接矩阵、vector 数组（邻接表的简化版）、链式前向星（邻接表的高效版）。

2.1 邻接矩阵：简单直接的 "二维表格"

邻接矩阵是最直观的存储方式，用一个二维数组**edges [N][N]**表示图，其中 edges [i][j]存储顶点 i 和 j 之间的边的信息。

存储逻辑：

不带权图：edges [i][j] = 1 表示有边，edges [i][j] = 0 表示无边；

带权图：edges [i][j] = 边的权值（有边），edges [i][j] = ∞（无穷大）表示无边；

无向图：edges [i][j] = edges [j][i]（因为边是双向的）；

有向图：edges [i][j] 只表示从 i 到 j 的边（单向）。

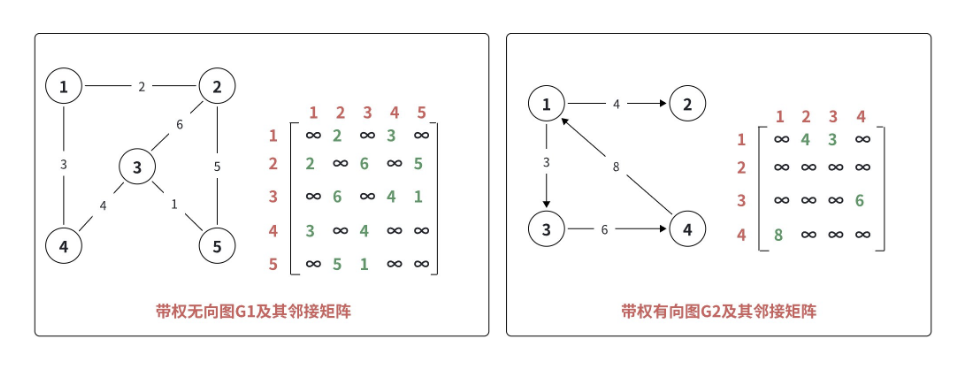
代码实现（带权无向图）：

cpp 复制代码

#include <iostream>
#include <cstring>
using namespace std;

const int N = 1010;  // 顶点数上限
int n, m;            // n：顶点数，m：边数
int edges[N][N];     // 邻接矩阵，存储边的权值

int main() {
    memset(edges, -1, sizeof edges);  // 初始化：-1表示无边
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int a, b, c;
        cin >> a >> b >> c;  // a和b是顶点，c是边的权值
        edges[a][b] = c;
        edges[b][a] = c;     // 无向图，双向存储
    }
    return 0;
}

优缺点分析：

优点：
1. 实现简单，直观易懂；
2. 查询两个顶点之间是否有边、边的权值，时间复杂度 O (1)；
3. 适合稠密图（边数多），因为稠密图的邻接矩阵利用率高。
缺点：
1. 空间复杂度 O (N²)，N 较大时（比如 N=1e5）会爆内存（1e10 个元素，根本存不下）；
2. 遍历一个顶点的所有邻边时，需要遍历整个数组（O (N) 时间），效率低；
3. 不适合稀疏图（大部分元素是∞或 0，浪费空间）。

适用场景：

稠密图、顶点数较少（N≤1e3）、需要频繁查询边是否存在的场景。

2.2 vector 数组：灵活高效的 "邻接表"

邻接表是稀疏图的首选存储方式，核心思想是：为每个顶点建立一个链表（或数组），存储该顶点的所有邻边。vector 数组是邻接表的简化实现，用 **vector<PII> edges [N]**表示，其中 **edges [u]**存储顶点 u 的所有邻边（每个元素是 pair<int, int>，第一个值是邻接顶点 v，第二个值是边的权值 w）。

存储逻辑：

每个顶点 u 对应一个 vector，vector 中的元素是 (v, w)，表示 u 到 v 有一条权值为 w 的边；

无向图：添加边 **(u, v, w)**时，需要同时在 edges [u]中添加(v, w)，在 **edges [v]**中添加 (u, w)；

有向图：只需要在 edges [u] 中添加**(v, w)**。

代码实现（带权无向图）：

cpp 复制代码

#include <iostream>
#include <vector>
using namespace std;

typedef pair<int, int> PII;  // 第一个元素：邻接顶点，第二个元素：边权
const int N = 1e5 + 10;      // 顶点数上限（支持1e5个顶点，稀疏图无压力）
int n, m;
vector<PII> edges[N];        // 邻接表：edges[u]存储u的所有邻边

int main() {
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        edges[a].push_back({b, c});  // a→b，权值c
        edges[b].push_back({a, c});  // 无向图，添加反向边
    }
    return 0;
}

优缺点分析：

优点：
1. 空间复杂度 O (N + M)，只存储实际存在的边，适合稀疏图（M 远小于 N²）；
2. 遍历一个顶点的所有邻边时，直接遍历对应的 vector，时间复杂度 O (度 (u))，效率高；
3. 支持顶点数多的场景（比如 N=1e5），不会爆内存。
缺点：
1. 查询两个顶点之间是否有边，需要遍历其中一个顶点的 vector，时间复杂度 O (度 (u))，比邻接矩阵慢；
2. 实现比邻接矩阵稍复杂（需要用 pair 或结构体）。

适用场景：

稀疏图、顶点数多（N≤1e5）、需要频繁遍历邻边的场景（比如 DFS、BFS、最短路算法）。

2.3 链式前向星：极致高效的 "邻接表"

链式前向星是邻接表的另一种实现方式，基于数组模拟链表，比 vector 数组更节省内存、访问速度更快，是算法竞赛中的 "常客"，尤其适合处理大规模稀疏图。

核心结构：

需要四个数组：

h [N]：头指针数组，h [u] 存储顶点 u 的第一条边的索引；

e [M]：边数组，e [id] 存储第 id 条边的终点 v；

ne [M]：next 指针数组，ne [id] 存储第 id 条边的下一条边的索引；

w [M]：权值数组，w [id] 存储第 id 条边的权值。

存储逻辑：

每条边用一个索引 id 标识，通过**ne [id]**串联起同一个顶点的所有边；

添加边时，采用**"头插法"**：将新边插入到顶点 u 的边链表的头部（更新 h [u] 为新边的 id）；

无向图需要添加两条方向相反的边。

代码实现（带权无向图）：

cpp 复制代码

#include <iostream>
using namespace std;

const int N = 1e5 + 10;  // 顶点数上限
const int M = 2e5 + 10;  // 边数上限（无向图每条边存两次，所以M要翻倍）
int h[N], e[M], ne[M], w[M], id;  // 链式前向星核心数组
int n, m;

// 添加一条边：a→b，权值c
void add(int a, int b, int c) {
    id++;          // 边的唯一索引
    e[id] = b;     // 边的终点
    w[id] = c;     // 边的权值
    ne[id] = h[a]; // 新边的下一条边是a原来的第一条边
    h[a] = id;     // a的第一条边更新为当前新边
}

int main() {
    cin >> n >> m;
    memset(h, 0, sizeof h);  // 初始化头指针数组为0（0表示无后续边）
    for (int i = 1; i <= m; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);  // 添加a→b的边
        add(b, a, c);  // 无向图，添加b→a的边
    }
    return 0;
}

优缺点分析：

优点：
1. 空间复杂度 O (N + M)，比 vector 数组更节省内存（vector 有额外的容器开销）；
2. 访问速度极快（数组访问比 vector 的迭代器快）；
3. 适合大规模稀疏图（比如 N=1e5，M=2e5），是算法竞赛的首选存储方式。
缺点：
1. 实现比 vector 数组复杂，需要理解链表的头插法；
2. 不支持随机访问边，只能按顺序遍历。

适用场景：

算法竞赛、大规模稀疏图、对时间和内存要求极高的场景。

三种存储方式对比总结

存储方式	空间复杂度	查询边是否存在	遍历邻边效率	适用场景
邻接矩阵	O(N²)	O(1)	O(N)	稠密图、N 较小（≤1e3）
vector 数组（邻接表）	O(N+M)	O (度 (u))	O (度 (u))	稀疏图、N 较大（≤1e5）、日常开发
链式前向星	O(N+M)	O (度 (u))	O (度 (u))	稀疏图、大规模数据、算法竞赛

日常开发中，vector 数组是性价比最高的选择（兼顾简洁性和效率）；算法竞赛中，链式前向星更适合处理超大规模数据；稠密图直接用邻接矩阵。

三、图的遍历：如何 "走遍" 图中的所有顶点

图的遍历是指从某个顶点出发，按照一定规则访问图中所有顶点，且每个顶点只访问一次。这是图论算法的基础（比如最短路、拓扑排序、连通分量查询都依赖遍历）。常用的遍历算法有两种：DFS（深度优先搜索）和 BFS（广度优先搜索）。

3.1 DFS：深度优先搜索 ------"一条路走到黑"

DFS 的核心思想是：从起点出发，沿着一条路径一直走到底，直到无法继续前进，然后回溯到上一个顶点，选择另一条未探索的路径，重复这个过程，直到所有顶点都被访问。

可以用一个生活例子理解：你走进一个迷宫，每次选择一条未走过的岔路一直走，走到死胡同就退回来，换另一条岔路，直到走出迷宫（访问所有房间）。

关键要点：

需要一个布尔数组 **st [N]**标记顶点是否已被访问（避免重复访问）；

递归实现（简洁）或栈实现（非递归，适合大规模数据，避免栈溢出）；

遍历顺序：深度优先，可能先访问远的顶点，再回溯访问近的顶点。

代码实现（三种存储方式）：

1. 邻接矩阵存储的 DFS

cpp 复制代码

#include <iostream>
#include <cstring>
using namespace std;

const int N = 1010;
int n, m;
int edges[N][N];  // 邻接矩阵
bool st[N];       // 标记是否访问过

// 从顶点u开始DFS
void dfs(int u) {
    cout << u << " ";  // 访问顶点u
    st[u] = true;      // 标记为已访问
    // 遍历所有顶点，找u的邻边
    for (int v = 1; v <= n; v++) {
        // 如果u和v之间有边，且v未被访问
        if (edges[u][v] != -1 && !st[v]) {
            dfs(v);  // 递归访问v
        }
    }
}

int main() {
    memset(edges, -1, sizeof edges);
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        edges[a][b] = c;
        edges[b][a] = c;
    }
    // 假设从顶点1开始遍历（如果图非连通，需要遍历所有未访问的顶点）
    for (int i = 1; i <= n; i++) {
        if (!st[i]) {
            dfs(i);
        }
    }
    return 0;
}

2. vector 数组（邻接表）存储的 DFS

cpp 复制代码

#include <iostream>
#include <vector>
using namespace std;

typedef pair<int, int> PII;
const int N = 1e5 + 10;
int n, m;
vector<PII> edges[N];  // 邻接表
bool st[N];            // 标记是否访问过

void dfs(int u) {
    cout << u << " ";
    st[u] = true;
    // 遍历u的所有邻边
    for (auto& t : edges[u]) {
        int v = t.first;  // 邻接顶点
        // int w = t.second;  // 边权（遍历不需要时可忽略）
        if (!st[v]) {
            dfs(v);
        }
    }
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        edges[a].push_back({b, c});
        edges[b].push_back({a, c});
    }
    // 处理非连通图
    for (int i = 1; i <= n; i++) {
        if (!st[i]) {
            dfs(i);
        }
    }
    return 0;
}

3. 链式前向星存储的 DFS

cpp 复制代码

#include <iostream>
using namespace std;

const int N = 1e5 + 10;
const int M = 2e5 + 10;
int h[N], e[M], ne[M], w[M], id;
int n, m;
bool st[N];

void add(int a, int b, int c) {
    id++;
    e[id] = b;
    w[id] = c;
    ne[id] = h[a];
    h[a] = id;
}

void dfs(int u) {
    cout << u << " ";
    st[u] = true;
    // 遍历u的所有邻边（链式前向星遍历方式）
    for (int i = h[u]; i; i = ne[i]) {
        int v = e[i];  // 邻接顶点
        // int w = ::w[i];  // 边权（遍历不需要时可忽略）
        if (!st[v]) {
            dfs(v);
        }
    }
}

int main() {
    memset(h, 0, sizeof h);
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
        add(b, a, c);
    }
    // 处理非连通图
    for (int i = 1; i <= n; i++) {
        if (!st[i]) {
            dfs(i);
        }
    }
    return 0;
}

DFS 的应用场景：

连通分量查询（判断图是否连通、找所有连通分量）；

路径搜索（比如迷宫问题、单词接龙）；

拓扑排序（递归实现）；

生成树构建。

注意事项：

递归实现的 DFS 在顶点数较多时（比如 N=1e4）会导致栈溢出，此时需要用非递归实现（用栈模拟递归过程）；

非连通图需要遍历所有未访问的顶点，确保所有顶点都被访问。

3.2 BFS：广度优先搜索 ------"一层一层剥开"

BFS 的核心思想是：从起点出发，先访问起点的所有邻接顶点（第一层），再依次访问每个邻接顶点的邻接顶点（第二层），以此类推，直到所有顶点都被访问。

生活例子：你站在一个广场中央，先和身边的人打招呼（第一层），再和身边人的朋友打招呼（第二层），直到所有在场的人都打过招呼。

关键要点：

需要一个**队列（queue）**存储待访问的顶点；

需要一个布尔数组 st [N] 标记顶点是否已被访问；

遍历顺序：广度优先，先访问近的顶点，再访问远的顶点（适合找最短路径，比如无权图的最短路）。

代码实现（三种存储方式）：

1. 邻接矩阵存储的 BFS

cpp 复制代码

#include <iostream>
#include <cstring>
#include <queue>
using namespace std;

const int N = 1010;
int n, m;
int edges[N][N];
bool st[N];

void bfs(int u) {
    queue<int> q;
    q.push(u);  // 起点入队
    st[u] = true;  // 标记为已访问
    while (!q.empty()) {
        int a = q.front();  // 取出队头顶点
        q.pop();
        cout << a << " ";  // 访问顶点
        // 遍历所有顶点，找a的邻边
        for (int v = 1; v <= n; v++) {
            if (edges[a][v] != -1 && !st[v]) {
                q.push(v);  // 邻接顶点入队
                st[v] = true;  // 标记为已访问（避免重复入队）
            }
        }
    }
}

int main() {
    memset(edges, -1, sizeof edges);
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        edges[a][b] = c;
        edges[b][a] = c;
    }
    // 处理非连通图
    for (int i = 1; i <= n; i++) {
        if (!st[i]) {
            bfs(i);
        }
    }
    return 0;
}

2. vector 数组（邻接表）存储的 BFS

cpp 复制代码

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

typedef pair<int, int> PII;
const int N = 1e5 + 10;
int n, m;
vector<PII> edges[N];
bool st[N];

void bfs(int u) {
    queue<int> q;
    q.push(u);
    st[u] = true;
    while (!q.empty()) {
        int a = q.front();
        q.pop();
        cout << a << " ";
        // 遍历a的所有邻边
        for (auto& t : edges[a]) {
            int v = t.first;
            if (!st[v]) {
                q.push(v);
                st[v] = true;
            }
        }
    }
}

int main() {
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        edges[a].push_back({b, c});
        edges[b].push_back({a, c});
    }
    // 处理非连通图
    for (int i = 1; i <= n; i++) {
        if (!st[i]) {
            bfs(i);
        }
    }
    return 0;
}

3. 链式前向星存储的 BFS

cpp 复制代码

#include <iostream>
#include <queue>
using namespace std;

const int N = 1e5 + 10;
const int M = 2e5 + 10;
int h[N], e[M], ne[M], w[M], id;
int n, m;
bool st[N];

void add(int a, int b, int c) {
    id++;
    e[id] = b;
    w[id] = c;
    ne[id] = h[a];
    h[a] = id;
}

void bfs(int u) {
    queue<int> q;
    q.push(u);
    st[u] = true;
    while (!q.empty()) {
        int a = q.front();
        q.pop();
        cout << a << " ";
        // 遍历a的所有邻边
        for (int i = h[a]; i; i = ne[i]) {
            int v = e[i];
            if (!st[v]) {
                q.push(v);
                st[v] = true;
            }
        }
    }
}

int main() {
    memset(h, 0, sizeof h);
    cin >> n >> m;
    for (int i = 1; i <= m; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
        add(b, a, c);
    }
    // 处理非连通图
    for (int i = 1; i <= n; i++) {
        if (!st[i]) {
            bfs(i);
        }
    }
    return 0;
}

BFS 的应用场景：

无权图的最短路径（比如找两个顶点之间的最短边数）；

层序遍历（比如树的层序遍历，本质是 BFS）；

连通分量查询；

拓扑排序（队列实现）。

注意事项：

顶点入队时必须立即标记为已访问（st [v] = true），否则可能会被多次入队，导致队列溢出和时间复杂度升高；

非连通图需要遍历所有未访问的顶点，确保所有顶点都被访问。

DFS 与 BFS 对比总结

| | 遍历方式 | 实现方式 | 遍历顺序 | 空间复杂度 | 适用场景 | |------|--------|--------------|-------|----------------| | DFS | 递归 / 栈 | 深度优先（一条路走到黑） | O(N) | 连通分量、路径搜索、拓扑排序 | | BFS | 队列 | 广度优先（一层一层） | O(N) | 无权图最短路、层序遍历 | |
|-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|

总结

图论的世界远比我们想象的精彩，掌握了基础的概念、存储和遍历，你就已经打开了算法大门的一半。接下来，就带着这些知识去刷题实战吧 ------ 只有亲手敲代码、解决实际问题，才能真正将知识内化为能力！

如果这篇文章对你有帮助，别忘了点赞、收藏、转发三连～后续还会更新最短路、最小生成树、拓扑排序等进阶内容，关注我，一起玩转图论！

【算法基础篇】（三十四）图论基础深度解析：从概念到代码，玩转图的存储与遍历

目录

前言

一、图的基本概念：搞懂这些，才算真正入门

1.1 图的定义：不止是 "点" 和 "线" 的组合

1.2 有向图和无向图：关系是 "双向奔赴" 还是 "单向暗恋"

无向图：双向可达的 "对等关系"

有向图：单向通行的 "依赖关系"

1.3 简单图与多重图：关系是否 "唯一"

关键定义：

分类：

1.4 稠密图和稀疏图：关系是 "密集" 还是 "稀疏"

1.5 顶点的度：每个 "人" 有多少 "关系"

无向图中的度：

有向图中的度：

1.6 路径：从 "起点" 到 "终点" 的路线

1.7 简单路径与回路：路线是否 "重复"、是否 "闭环"

1.8 路径长度和带权路径长度：路线的 "距离" 或 "成本"

不带权图：

带权图（网络）：

1.9 子图：从 "大网络" 中提取 "小网络"

1.10 连通图与连通分量："网络" 是否 "互通"

关键定义：

1.11 生成树：连通图的 "最小骨架"

二、图的存储：如何用代码 "记录" 图的结构

2.1 邻接矩阵：简单直接的 "二维表格"

存储逻辑：

代码实现（带权无向图）：

优缺点分析：

适用场景：

2.2 vector 数组：灵活高效的 "邻接表"

存储逻辑：

代码实现（带权无向图）：

优缺点分析：

适用场景：

2.3 链式前向星：极致高效的 "邻接表"

核心结构：

存储逻辑：

代码实现（带权无向图）：

优缺点分析：

适用场景：

三种存储方式对比总结

三、图的遍历：如何 "走遍" 图中的所有顶点

3.1 DFS：深度优先搜索 ------"一条路走到黑"

关键要点：

代码实现（三种存储方式）：

1. 邻接矩阵存储的 DFS

2. vector 数组（邻接表）存储的 DFS

3. 链式前向星存储的 DFS

DFS 的应用场景：

注意事项：

3.2 BFS：广度优先搜索 ------"一层一层剥开"

关键要点：

代码实现（三种存储方式）：

1. 邻接矩阵存储的 BFS

2. vector 数组（邻接表）存储的 BFS

3. 链式前向星存储的 BFS

BFS 的应用场景：

注意事项：

DFS 与 BFS 对比总结

总结