力扣题目-下一个排列
整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。
例如,arr = [1,2,3] ,以下这些都可以视作 arr 的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。
整数数组的下一个排列是指其整数的下一个字典序更大的排列。更正式地,如果数组的所有排列根据其字典顺序从小到大排列在一个容器中,那么数组的下一个排列就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列,那么这个数组必须重排为字典序最小的排列(即,其元素按升序排列)。
例如,arr = [1,2,3] 的下一个排列是 [1,3,2] 。
类似地,arr = [2,3,1] 的下一个排列是 [3,1,2] 。
而 arr = [3,2,1] 的下一个排列是 [1,2,3] ,因为 [3,2,1] 不存在一个字典序更大的排列。
给你一个整数数组 nums ,找出 nums 的下一个排列。
必须原地修改,只允许使用额外常数空间。

分析:
首先考虑全部是倒序的情况下,比如3 2 1,那么这个时候只需要把所有的数字反转一下变成1 2 3就可以了。下面考虑的是其他一般的情况。
第一步:可以从右往左看,找到最左边需要改变的数字,就是去看个位 十位 百位 千位,举个例子来理解。
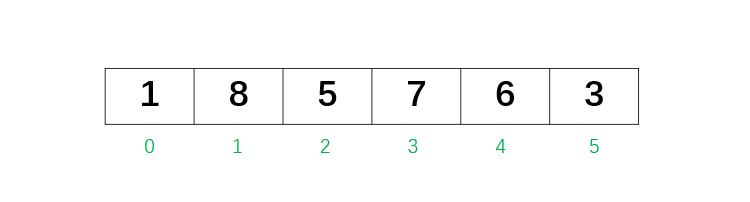
比如nums = [1, 8, 5, 7, 6, 3],如果找到的那个数字是7,那么就说明7左边的数字完全不用变,只需要改变个位十位百位就可以了。我们找到的这个数字当然是越接近右边(个位)更好,因为我们要实现的是增幅最小的百位以及后面的数字改变肯定比千位数字改变增幅最小。
如何找到这个数字,从右边往左边寻找,每一个都和相邻的比较,找到第一个下降的数字。设置一个 i 指向倒数第二位,用 i 和 i+1 位置的值进行比较。
-
i = 4,检查 nums[4] = 6 和 nums[5] = 3,发现 6 > 3,继续向前查找。
-
i = 3,检查 nums[3] = 7 和 nums[4] = 6,发现 7 > 6,继续向前查找。
-
i = 2,检查 nums[2] = 5 和 nums[3] = 7,发现 5 < 7,找到了下降的位置,i = 2。
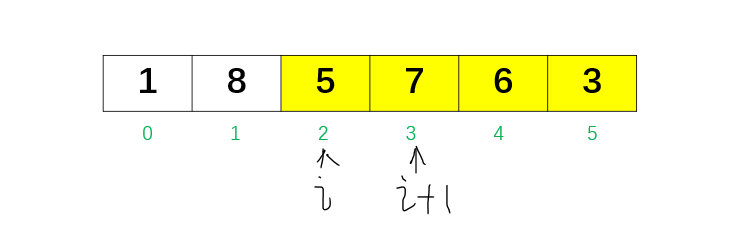
此时我们可以确定要改变的就是5 7 6 3这几个数字,而前面的是不需要改变的。反过来想,如果需要改变的只是后三位数763,那么763这三个数字已经是倒序排序的,是这三个数字组成的最大的组合了,不管怎么组合都不可能比763更大,也就无法完成我们的目标让这个序列变得更大。
第二步:从右向左找到第一个比 nums[i] 大的数字。这一步是为了确定 i 所在的位置对应的5变成什么,要想实现最小的增幅,那么就要找到 5后面的比5大的数,和5进行交换。显然,我们应该找到5右边比5大,但是增幅最小的那个数字。由于5后面的数字已经是降序,所以只需要从右往左找,找到的第一个比5大的数就行了。可以设置一个 j 不断左移来进行查找。
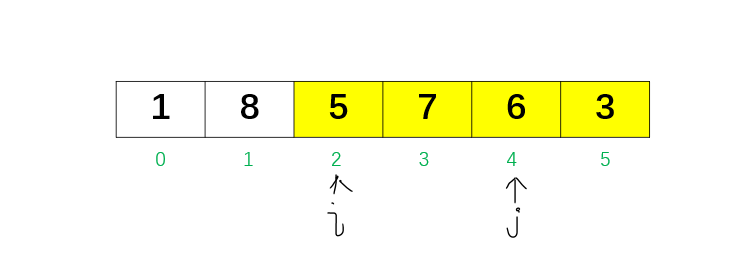
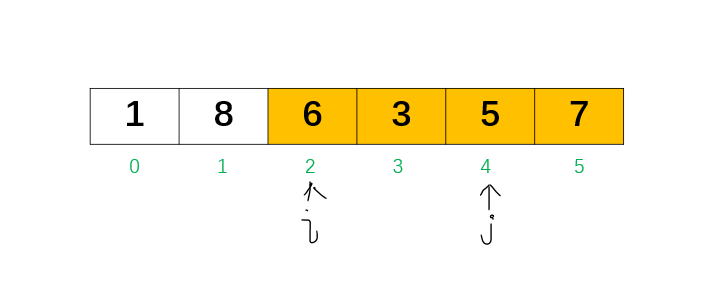
从后往前找到 j = 4,比 5 大的最小元素是 6,此时,交换 i 与 j 位置的数字nums[i] 和 nums[j],得到 [1, 8, 6, 7, 5, 3]。
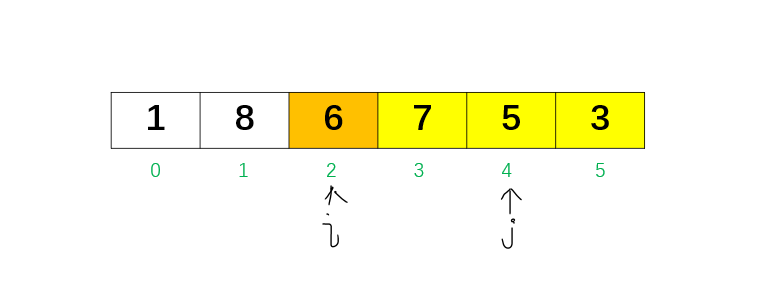
这时 i 对应的6已经确定,前三位已无需改动。
第三步:修改 i 之后的后三位数,这时由于后面的数已经是倒序排的,要使增幅最小,只需要把后面的那一串数字进行反转就可以。因为原先数字就是降序的,我们只是换了位置 i 和位置 j 的数,j 是6,它的左边的数一开始就比 j 大,右边的数一开始就比 j 小,把5换过去之后也一定会满足这种情况。
反转 i 后面的部分,得到 [1, 8, 6, 3, 5, 7]。
以下是具体C++代码实现:
cpp
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
class Solution {
public:
void nextPermutation(vector<int>& nums) {
int n = nums.size();
int i = n - 2;
while (i >= 0 && nums[i] >= nums[i + 1])
i--;
if (i >= 0) {
int j = n - 1;
while (nums[j] <= nums[i])
j--;
swap(nums[i], nums[j]);
}
reverse(nums.begin() + i + 1, nums.end());
}
};