动态规划可以说是整个算法基础篇中,最难的⼀章:
• ⾸先,⼊⻔难。刚开始接触动态规划,你会觉得这玩意有点晦涩 + ⽞学,稀⾥糊涂的就把问题解决 了。不⽤担⼼,等做过五六道题⽬之后,就能理解动态规划是如何解决问题的;--- 坚持学、重复学
• 其次,题型多。不仅算法基础篇会讲到动态规划,在算法提⾼篇还会再讲。动态规划细分的话,可 以分出⼗⼏种类型。所以,学习的成本是⽐较⾼的;
• 最后,题⽬难。在竞赛中,如果遇到动态规划的问题,只要不是经典题型,那么⼤概率就是以压轴 题的形式出现。 但是,即使很难,我们也要慢慢去学习。想取得好成绩,动态规划是避不开的。不过⼤家放⼼,往后 讲解的时候,我会循序渐进的进⾏,相信⼤家都是可以听得懂的。
1. ⼊⻔:从记忆化搜索到动态规划
1. 记忆化搜索
在搜索的过程中,如果搜索树中有很多重复的结点,此时可以通过⼀个 "备忘录",记录第⼀次搜索到 的结果。当下⼀次搜索到这个结点时,直接在 "备忘录" ⾥⾯找结果。其中,搜索树中的⼀个⼀个结 点,也称为⼀个⼀个状态。
⽐如经典的斐波那契数列问题:
cpp
int f[N]; // 备忘录
int fib(int n)
{
// 搜索之前先往备忘录⾥⾯瞅瞅
if(f[n] != -1) return f[n];
if(n == 0 || n == 1) return f[n] = n;
// 返回之前,把结果记录在备忘录中
f[n] = fib(n - 1) + fib(n - 2);
return f[n];
}2. 递归改递推
在⽤记忆化搜索解决斐波那契问题时,如果关注 "备忘录" 的填写过程,会发现它是从左往右依次填写 的。当 位置前⾯的格⼦填写完毕之后,就可以根据格⼦⾥⾯的值计算出 位置的值。所以,整个 递归过程,我们也可以改写成循环的形式,也就是递推
cpp
int f[N]; // f[i] 表⽰:第 i 个斐波那契数
int fib(int n)
{
// 初始化前两个格⼦
f[0] = 0; f[1] = 1;
// 按照递推公式计算后⾯的值
for(int i = 2; i <= n; i++)
{
f[i] = f[i - 1] + f[i - 2];
}
// 返回结果
return f[n];
}3. 动态规划
动态规划(Dynamic Programming,简称DP) 是⼀种⽤于解决多阶段决策问题的算法思想。它通过 将复杂问题分解为更⼩的⼦问题,并存储⼦问题的解(通常称为"状态"),从⽽避免重复计算,提 ⾼效率。因此,动态规划⾥,蕴含着分治与剪枝思想。
上述通过记忆化搜索以及递推解决斐波那契数列的⽅式,其实都是动态规划。
注意:
• 动态规划中的相关概念其实远不⽌如此,还会有:重叠⼦问题、最优⼦结构、⽆后效性、有向⽆ 环图等等。
• 这些概念没有⼀段时间的沉淀是不可能完全理解的。可以等学过⼀段时间之后,再去接触这些概 念。不过,这些概念即使不懂,也不影响做题~
在递推形式的动态规划中,常⽤下⾯的专有名词来表述:
- 状态表⽰:指 f 数组中,每⼀个格⼦代表的含义。其中,这个数组也会称为 dp 数组,或者
dp 表。 - 状态转移⽅程:指 f 数组中,每⼀个格⼦是如何⽤其余的格⼦推导出来的。
- 初始化:在填表之前,根据题⽬中的默认条件或者问题的默认初始状态,将 f 数组中若⼲格⼦先
填上值
其实递推形式的动态规划中的各种表述,是可以对应到递归形式的:
• 状态表⽰ <---> 递归函数的意义;
• 状态转移⽅程 <---> 递归函数的主函数体;
• 初始化 <---> 递归函数的递归出⼝。
4. 如何利⽤动态规划解决问题
第⼀种⽅式当然就是记忆化搜索了:
• 先⽤递归的思想去解决问题;
• 如果有重复⼦问题,就改成记忆化搜索的形式。
第⼆种⽅式,直接使⽤ 递推 形式的动态规划解决:
- 定义状态表⽰:
⼀般情况下根据经验+递归函数的意义,赋予 dp 数组相应的含义。(其实还可以去蒙⼀个,如果
蒙的状态表⽰能解决问题,说明蒙对了。如果蒙错了,再换⼀个试~) - 推导状态转移⽅程:
根据状态表⽰以及题意,在 dp 表中分析,当前格⼦如何通过其余格⼦推导出来。 - 初始化:
根据题意,先将显⽽易⻅的以及边界情况下的位置填上值。 - 确定填表顺序:
根据状态转移⽅程,确定按照什么顺序来填表。 - 确定最终结果:
根据题意,在表中找出最终结果。
1.1 下楼梯
题⽬来源: 洛⾕
题⽬链接: P10250 [GESP样题 六级] 下楼梯
难度系数: ★
题目描述
顽皮的小明发现,下楼梯时每步可以走 1 个台阶、2 个台阶或 3 个台阶。现在一共有 N 个台阶,你能帮小明算算有多少种方案吗?
输入格式
输入一行,包含一个整数 N。
输出格式
输出一行一个整数表示答案。
输入输出样例
输入 #1复制
4输出 #1复制
7输入 #2复制
10输出 #2复制
274说明/提示
对全部的测试点,保证 1≤N≤60。
【解法】
因为上楼和下楼是⼀个 可逆 的过程,因此我们可以把下楼问题转化成上到第 n 个台阶,⼀共有多少种 ⽅案。
解法:动态规划
-
状态表⽰:
dp [ i ] 表⽰:⾛到第 i 个台阶的总⽅案数。
那最终结果就是在 dp [ n ] 处取到。 -
状态转移⽅程:
根据最后⼀步划分问题,⾛到第 i 个台阶的⽅式有三种:
a. 从 i − 1 台阶向上⾛ 1 个台阶,此时⾛到 i 台阶的⽅案就是 dp [ i − 1] ;
b. 从 i − 2 台阶向上⾛ 2 个台阶,此时⾛到 i 台阶的⽅案就是 dp [ i − 2] ;
c. 从 i − 3 台阶向上⾛ 3 个台阶,此时⾛到 i 台阶的⽅案就是 dp [ i − 3] ;
综上所述, dp [ i ] = dp [ i − 1] + dp [ i − 2] + dp [ i − 3] 。 -
初始化:
填i 位置的值时,⾄少需要前三个位置的值,因此需要初始化dp [0] = 1, dp [1] = 1, dp [2] = 2
,然后从i = 3 开始填。
或者初始化 dp [1] = 1, dp [2] = 2, dp [3] = 4 ,然后从 i = 4 开始填。 -
填表顺序:
明显是从左往右。
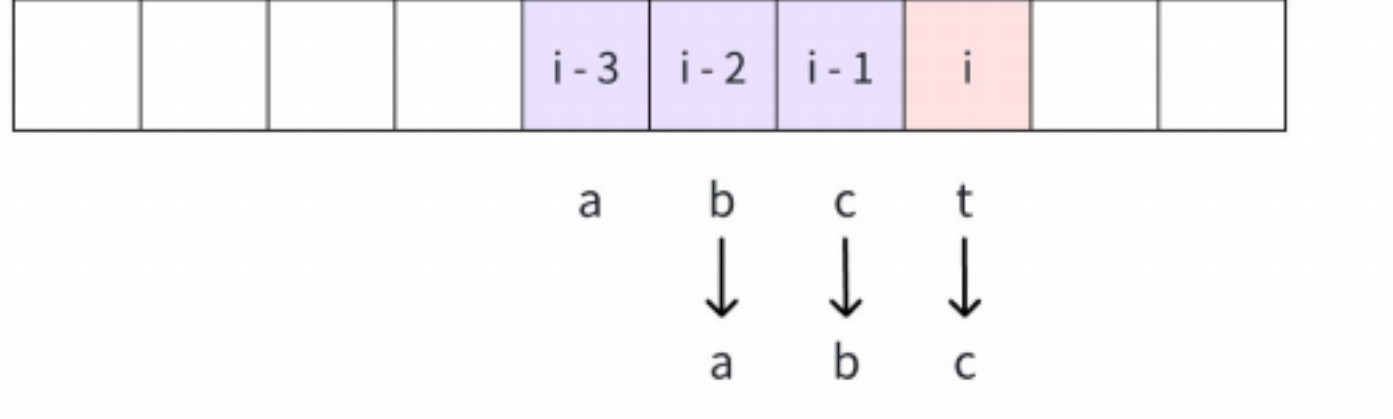
动态规划的空间优化:
我们发现,在填写 的值时,我们仅仅需要前三个格⼦的值,第 i-4个及其之前的格⼦的值已
经毫⽆⽤处了。因此,可以⽤三个变量记录 位置之前三个格⼦的值,然后在填完 位置的值之
后,滚动向后更新。
【参考代码】
cpp
#include <iostream>
using namespace std;
// 用long long避免数值溢出(N=60时结果远超int范围)
typedef long long LL;
int main() {
int n;
cin >> n;
// 版本1:数组版(直观,适合理解)
// LL dp[65] = {0}; // dp[i]表示走到第i阶的方案数
// // 初始化:
// dp[0] = 1; // 0阶(起点)有1种方案(不走)
// dp[1] = 1; // 1阶:只能走1步
// dp[2] = 2; // 2阶:1+1 / 2
// for (int i = 3; i <= n; i++) {
// dp[i] = dp[i-1] + dp[i-2] + dp[i-3];
// }
// cout << dp[n] << endl;
// 版本2:空间优化版(仅用3个变量,节省空间)
if (n == 1) {
cout << 1 << endl;
return 0;
}
if (n == 2) {
cout << 2 << endl;
return 0;
}
LL a = 1, b = 1, c = 2; // a=dp[i-3], b=dp[i-2], c=dp[i-1]
for (int i = 3; i <= n; i++) {
LL t = a + b + c; // dp[i] = dp[i-1]+dp[i-2]+dp[i-3]
a = b; // 滚动更新:a变为新的dp[i-3]
b = c; // b变为新的dp[i-2]
c = t; // c变为新的dp[i-1]
}
cout << c << endl;
return 0;
}1.2 数字三⻆形
题⽬来源: 洛⾕
题⽬链接: P1216 [USACO1.5] [IOI1994]数字三⻆形 Number Triangles
难度系数: ★
题目描述
观察下面的数字金字塔。
写一个程序来查找从最高点到底部任意处结束的路径,使路径经过数字的和最大。每一步可以走到左下方的点也可以到达右下方的点。
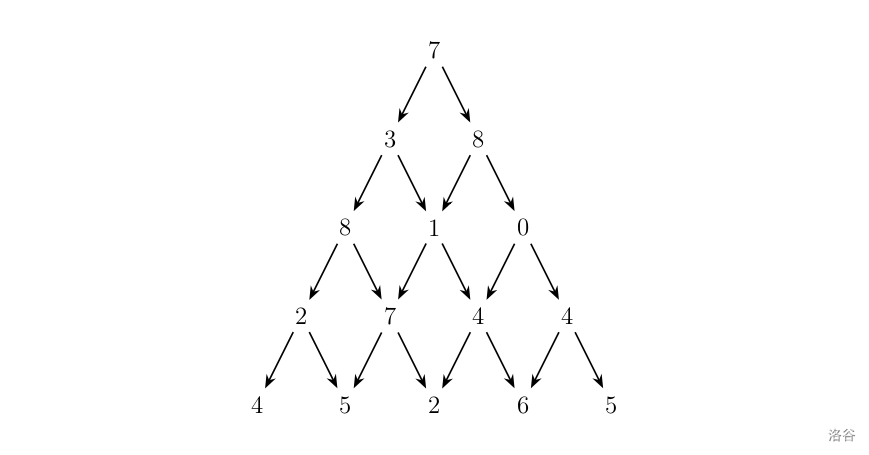
在上面的样例中,从 7→3→8→7→5 的路径产生了最大权值。
输入格式
第一个行一个正整数 r,表示行的数目。
后面每行为这个数字金字塔特定行包含的整数。
输出格式
单独的一行,包含那个可能得到的最大的和。
输入输出样例
输入 #1复制
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5 输出 #1复制
30说明/提示
【数据范围】
对于 100% 的数据,1≤r≤1000,所有输入在 [0,100] 范围内。
题目翻译来自 NOCOW。
IOI1994 Day1T1 / USACO Training Section 1.5。
【解法】
学习动态规划最经典的⼊⻔题。
解法:动态规划
- 状态表⽰:
dp [ i ][ j ] 表⽰:⾛到 [ i , j ] 位置的最⼤权值。
那最终结果就是在 dp 表的第 n ⾏中,所有元素的最⼤值。 - 状态转移⽅程:
根据最后⼀步划分问题,⾛到 [ i , j ] 位置的⽅式有两种:
a. 从 [ i − 1, j ] 位置向下⾛⼀格,此时⾛到 [ i , j ] 位置的最⼤权值就是 dp [ i − 1][ j ] ;
b. 从 [ i − 1, j − 1] 位置向右下⾛⼀格,此时⾛到 [ i , j ] 位置的最⼤权值就是 dp [ i − 1][ j − 1] ;
综上所述,应该是两种情况的最⼤值再加上 [ i , j ] 位置的权值:
dp [ i ][ j ] = max ( dp [ i − 1][ j ], dp [ i − 1][ j − 1]) + a [ i ][ j ] 。 - 初始化:
因为 dp 表被 0 包围着,并不影响我们的最终结果,因此可以直接填表。
思考,如果权值出现负数的话,需不需要初始化?
◦ 此时可以全都初始化为 −∞ ,负⽆穷⼤在取 max 之后,并不影响最终结果。 - 填表顺序:
从左往右填写每⼀⾏,每⼀⾏从左往右。
动态规划的空间优化:
我们发现,在填写第 i ⾏的值时,我们仅仅需要前⼀⾏的值,并不需要第 i − 2 以及之前⾏的值。
因此,我们可以只⽤⼀个⼀维数组来记录上⼀⾏的结果,然后在这个数组上更新当前⾏的值。
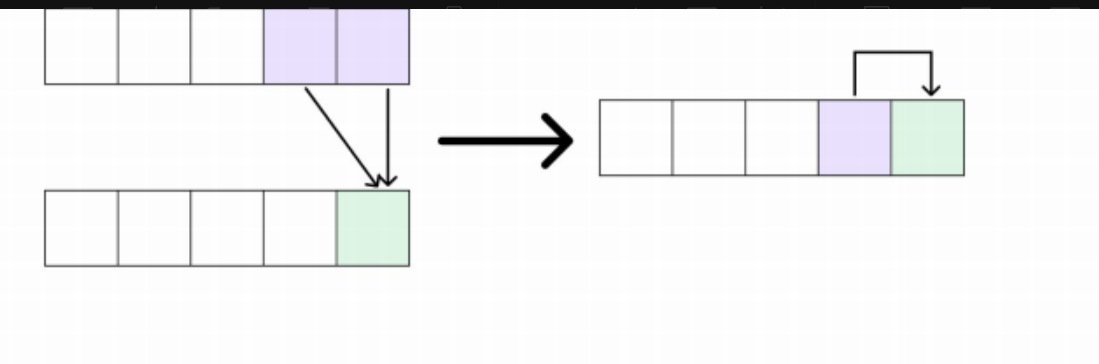
需要注意,当⽤因为我们当前这个位置的值需要左上⻆位置的值,因此滚动数组优化的时候,要改变 第⼆维的遍历顺序。
【参考代码】
cpp
#include <iostream>
#include <algorithm> // 必须包含:max函数依赖此头文件
using namespace std;
const int N = 1010; // 适配r≤1000的范围
int r; // 金字塔的行数
int a[N][N]; // 存储金字塔的数值(a[i][j]表示第i行第j列)
int f[N]; // 空间优化:一维DP数组,f[j]表示走到当前行第j列的最大和
int main() {
// 加速输入输出(处理1000行数据时必备)
ios::sync_with_stdio(false);
cin.tie(nullptr);
// 1. 输入金字塔行数和数值
cin >> r;
for (int i = 1; i <= r; i++) { // 行从1开始计数
for (int j = 1; j <= i; j++) { // 第i行有i列
cin >> a[i][j];
}
}
// 2. 空间优化版DP:一维数组逆序遍历
for (int i = 1; i <= r; i++) {
// 逆序遍历列(j从i到1):避免覆盖上一行的f[j-1]
for (int j = i; j >= 1; j--) {
// 状态转移:
// 二维版:f[i][j] = max(f[i-1][j], f[i-1][j-1]) + a[i][j]
// 一维版:f[j] 保留上一行的结果,f[j-1]也未被覆盖
f[j] = max(f[j], f[j - 1]) + a[i][j];
}
}
// 3. 找最后一行的最大值(所有路径的终点)
int max_sum = 0;
for (int j = 1; j <= r; j++) {
max_sum = max(max_sum, f[j]);
}
// 4. 输出结果
cout << max_sum << endl;
return 0;
}2. 线性 dp
线性dp 是动态规划问题中最基础、最常⻅的⼀类问题。它的特点是状态转移只依赖于前⼀个或前⼏个 状态,状态之间的关系是线性的,通常可以⽤⼀维或者⼆维数组来存储状态。
我们在⼊⻔阶段解决的《下楼梯》以及《数字三⻆形》其实都是线性 dp,⼀个是⼀维的,另⼀是⼆ 维的。
2.1 基础线性 dp
2.1.1 台阶问题
题⽬来源: 洛⾕
题⽬链接: P1192 台阶问题
难度系数: ★
题目描述
有 N 级台阶,你一开始在底部,每次可以向上迈 1∼K 级台阶,问到达第 N 级台阶有多少种不同方式。
输入格式
两个正整数 N,K。
输出格式
一个正整数 ans(mod100003),为到达第 N 级台阶的不同方式数。
输入输出样例
输入 #1复制
5 2输出 #1复制
8说明/提示
- 对于 20% 的数据,1≤N≤10,1≤K≤3;
- 对于 40% 的数据,1≤N≤1000;
- 对于 100% 的数据,1≤N≤100000,1≤K≤100。
【解法】
斐波那契数列模型
- 状态表⽰:
dp [ i ] 表⽰:⾛到 i 位置的⽅案数。
那么 dp [ n ] 就是我们要的结果。 - 状态转移⽅程:
可以从 区间内的台阶⾛到 位置,那么总⽅案数就是所有的 累加在⼀
起。 i − k ≤ j ≤ i − 1 i dp [ j ] 注意 i − k 不能⼩于 0 。 - 初始化:
dp [0] = 1 ,起始位置,为了让后续填表有意义。 - 填表顺序:
从左往右。
【参考代码】
cpp
#include <iostream> // 零件1:程序的"输入输出工具",没有它就没法读输入、打输出
using namespace std; // 零件2:简化代码的"快捷方式",不用每次写cout都加std::
// 零件3:定义两个"固定不变的数"(const=不变)
const int N = 1e5 + 10, MOD = 100003;
// N=1e5+10:1e5就是100000,意思是数组最多存100010个台阶的答案(够题目用)
// MOD=100003:题目要求答案取模(就是算完后除以100003取余数,防止数字太大装不下)
int n, k; // 零件4:两个变量,n是总台阶数,k是每次最多走的台阶数(比如输入5 2,n=5,k=2)
int f[N]; // 零件5:数组(像一排格子),f[i]表示"走到第i级台阶有多少种方法"(比如f[5]就是走到5级的答案)
int main() { // 零件6:程序的"主入口",所有代码从这里开始跑
// 零件7:加速输入输出(不用懂原理,记着加就行,不然输入大数字会慢)
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> k; // 零件8:读输入(比如输入5 2,就把n变成5,k变成2)
f[0] = 1; // 核心初始化:下面重点讲
// 核心循环1:算第1级到第n级台阶的方法数
for (int i = 1; i <= n; i++) {
// 核心循环2:算走到第i级台阶,能从哪些台阶走过来
for (int j = 1; j <= k && i - j >= 0; j++) {
f[i] = (f[i] + f[i - j]) % MOD; // 核心计算:下面重点讲
}
}
cout << f[n] << endl; // 零件9:输出答案(f[n]就是走到第n级台阶的方法数)
return 0; // 零件10:告诉电脑"程序跑完了,没问题"
}2.1.2 最⼤⼦段和
题⽬来源: 洛⾕
题⽬链接: P1115 最⼤⼦段和
难度系数: ★★
题目描述
给出一个长度为 n 的序列 a,选出其中连续且非空的一段使得这段和最大。
输入格式
第一行是一个整数,表示序列的长度 n。
第二行有 n 个整数,第 i 个整数表示序列的第 i 个数字 ai。
输出格式
输出一行一个整数表示答案。
输入输出样例
输入 #1复制
7
2 -4 3 -1 2 -4 3输出 #1复制
4说明/提示
样例 1 解释
选取 [3,5] 子段 {3,−1,2},其和为 4。
数据规模与约定
- 对于 40% 的数据,保证 n≤2×103。
- 对于 100% 的数据,保证 1≤n≤2×105,−104≤ai≤104。
【解法】
⼜ 遇⻅这道题了~
- 状态表⽰:
dp [ i ] 表⽰:以 i 位置元素为结尾的「所有⼦数组」中和的最⼤值。
那我们的最终结果应该是 dp 表⾥⾯的最⼤值。 - 状态转移⽅程:
dp [ i ] 的所有可能可以分为以下两种:
a. ⼦数组的⻓度为 1 :此时 dp [ i ] = a [ i ] ;
b. ⼦数组的⻓度⼤于1 :此时dp[i] 应该等于i-1 以 为结尾的「所有⼦数组」中和的最⼤值再
加上a[i] ,也就是dp[i-1]+a[i] 。
应该是两种情况下的最⼤值,因此可得转移⽅程: dp [ i ] = max ( a [ i ], dp [ i − 1] + a [ i ]) 。 - 初始化:
把第⼀个格⼦初始化为 0 ,往后填数的时候就不会影响最终结果。 - 填表顺序:
根据「状态转移⽅程」易得,填表顺序为「从左往右」。
【参考代码】
cpp
#include <iostream>
using namespace std;
const int N = 2e5 + 10; // 行1:定义一个常量N,值是200000+10,用来存数字的最大个数
int n; // 行2:定义变量n,用来存序列的长度(比如示例里的7)
int f[N]; // 行3:定义数组f,f[i]就是我们说的"第i个位置的小账"
int main() // 行4:程序的主入口,所有代码从这里开始执行
{
cin >> n; // 行5:输入n(比如示例里输入7)
int ret = -1e9; // 行6:定义变量ret,用来记所有小账里的最大值;初始值设成-1000000000(很小的数,保证任何数都比它大)
for(int i = 1; i <= n; i++) // 行7:循环,从1到n,逐个处理每个数字(i就是第i个位置)
{
int x; cin >> x; // 行8:输入第i个数字,存在x里(比如i=1时x=2,i=2时x=-4)
f[i] = max(f[i - 1] + x, x); // 行9:算第i个位置的小账!
ret = max(ret, f[i]); // 行10:更新最大值ret------把当前ret和f[i]比,留大的那个
}
cout << ret << endl; // 行11:输出最终的最大值(比如示例里的4)
return 0; // 行12:程序结束
}2.1.3 传球游戏
题⽬来源: 洛⾕
题⽬链接: P1057 [NOIP2008 普及组] 传球游戏
难度系数: ★★
题目描述
上体育课的时候,小蛮的老师经常带着同学们一起做游戏。这次,老师带着同学们一起做传球游戏。
游戏规则是这样的:n 个同学站成一个圆圈,其中的一个同学手里拿着一个球,当老师吹哨子时开始传球,每个同学可以把球传给自己左右的两个同学中的一个(左右任意),当老师再次吹哨子时,传球停止,此时,拿着球没有传出去的那个同学就是败者,要给大家表演一个节目。
聪明的小蛮提出一个有趣的问题:有多少种不同的传球方法可以使得从小蛮手里开始传的球,传了 m 次以后,又回到小蛮手里。两种传球方法被视作不同的方法,当且仅当这两种方法中,接到球的同学按接球顺序组成的序列是不同的。比如有三个同学 1 号、2 号、3 号,并假设小蛮为 1 号,球传了 3 次回到小蛮手里的方式有 1→2→3→1 和 1→3→2→1,共 2 种。
输入格式
一行,有两个用空格隔开的整数 n,m(3≤n≤30,1≤m≤30)。
输出格式
1 个整数,表示符合题意的方法数。
输入输出样例
输入 #1复制
3 3输出 #1复制
2说明/提示
数据范围及约定
- 对于 40% 的数据,满足:3≤n≤30,1≤m≤20;
- 对于 100% 的数据,满足:3≤n≤30,1≤m≤30。
2008普及组第三题
【解法】
1. 状态表⽰:
f [i ][j ] 表⽰传了 i 次,落在第 j个⼈⼿⾥时的总⽅案数。
那么 f [m][1] 就是我们想要的结果。
2. 状态转移⽅程:
因为是⼀个环形结构,第⼀个位置和最后⼀个位置可以特殊处理:
a. 当 2 ≤ j ≤ n − 1 时,可以从 j − 1 或者 j + 1 传到该位置,那么总⽅案数就是 f [i − 1][j − 1] + f [i − 1][j+ 1] ;
b. 当 j = 1 时,可以从 n 或者 2 传到该位置,那么总⽅案数就是 f [i − 1][n ] + f [i− 1][2] ;
c. 当 j = n 时,可以从 n− 1 或者 1 传到该位置,那么总⽅案数就是
f [i − 1][1] + f [i − 1][n− 1] 。
3. 初始化:
刚开始的状态设置为 1 ,让后续填表是正确的, f[0][1] = 1 。
4. 填表顺序:
⼀定要先循环次数,再循环位置。因为我们更新状态是从低次数更新⾼次数,也就是第⼀⾏更新第
⼆⾏。
因此填表顺序应该是从上往下每⼀⾏,⾏的顺序⽆所谓。
【参考代码】
cpp
#include <iostream>
using namespace std;
const int N = 50;
int n, m;
int f[N][N]; // f[i][j] 表⽰:传递了 i 次之后,落在了第 j 号同学⼿⾥的⽅案数
int main()
{
cin >> n >> m;
f[0][1] = 1;
for(int i = 1; i <= m; i++)
{
// 第⼀个⼈
f[i][1] = f[i - 1][2] + f[i - 1][n];
// 中间的同学
for(int j = 2; j < n; j++)
{
f[i][j] = f[i - 1][j - 1] + f[i - 1][j + 1];
}
// 最后⼀位同学
f[i][n] = f[i - 1][1] + f[i - 1][n - 1];
}
cout << f[m][1] << endl;
return 0;
}2.1.4 乌⻳棋
题⽬来源: 洛⾕
题⽬链接: P1541 [NOIP2010 提⾼组] 乌⻳棋
难度系数: ★★★
题目背景
NOIP2010 提高组 T2
题目描述
小明过生日的时候,爸爸送给他一副乌龟棋当作礼物。
乌龟棋的棋盘是一行 N 个格子,每个格子上一个分数(非负整数)。棋盘第 1 格是唯一的起点,第 N 格是终点,游戏要求玩家控制一个乌龟棋子从起点出发走到终点。
乌龟棋中 M 张爬行卡片,分成 4 种不同的类型(M 张卡片中不一定包含所有 4 种类型的卡片,见样例),每种类型的卡片上分别标有 1,2,3,4 四个数字之一,表示使用这种卡片后,乌龟棋子将向前爬行相应的格子数。游戏中,玩家每次需要从所有的爬行卡片中选择一张之前没有使用过的爬行卡片,控制乌龟棋子前进相应的格子数,每张卡片只能使用一次。
游戏中,乌龟棋子自动获得起点格子的分数,并且在后续的爬行中每到达一个格子,就得到该格子相应的分数。玩家最终游戏得分就是乌龟棋子从起点到终点过程中到过的所有格子的分数总和。
很明显,用不同的爬行卡片使用顺序会使得最终游戏的得分不同,小明想要找到一种卡片使用顺序使得最终游戏得分最多。
现在,告诉你棋盘上每个格子的分数和所有的爬行卡片,你能告诉小明,他最多能得到多少分吗?
输入格式
每行中两个数之间用一个空格隔开。
第 1 行 2 个正整数 N,M,分别表示棋盘格子数和爬行卡片数。
第 2 行 N 个非负整数,a1,a2,...,aN,其中 ai 表示棋盘第 i 个格子上的分数。
第 3 行 M 个整数,b1,b2,...,bM,表示 M 张爬行卡片上的数字。
输入数据保证到达终点时刚好用光 M 张爬行卡片。
输出格式
一个整数,表示小明最多能得到的分数。
输入输出样例
输入 #1复制
9 5
6 10 14 2 8 8 18 5 17
1 3 1 2 1输出 #1复制
73说明/提示
每个测试点 1s。
小明使用爬行卡片顺序为 1,1,3,1,2,得到的分数为 6+10+14+8+18+17=73。注意,由于起点是 1,所以自动获得第 1 格的分数 6。
对于 30% 的数据有 1≤N≤30,1≤M≤12。
对于 50% 的数据有 1≤N≤120,1≤M≤50,且 4 种爬行卡片,每种卡片的张数不会超过 20。
对于 100% 的数据有 1≤N≤350,1≤M≤120,且 4 种爬行卡片,每种卡片的张数不会超过 40;0≤ai≤100(1≤i≤N),1≤bi≤4(1≤i≤M)。
【解法】
- 状态表⽰:f [ i ][ a ][ b ][ c ][ d ] 表⽰:⾛到 i位置时,编号为 1234的卡⽚分别⽤了 abcd张,此时的最⼤分 数。
我们发现,当1234 ⽤的卡⽚数确定之后,⾛到的位置 可以计算出来,其中
i = 1 + a + 2 b + 3 c + 4 d
因此状态表⽰可以优化掉⼀维,变成f [ a ][ b ][ c ][ d ] ,表⽰:编号为1234 的卡⽚分别⽤了abcd张,此时的最⼤分数。 - 状态转移⽅程:
设根据最后⼀次⽤的卡⽚种类,分情况讨论:
a. 如果 a > 0 ,并且最后⼀张⽤ 1 卡⽚,最⼤分数为: f [ a − 1][ b ][ c ][ d ] + nums [ i ] ;
b. 如果 b > 0 ,并且最后⼀张⽤ 2 卡⽚,最⼤分数为: f [ a ][ b − 1][ c ][ d ] + nums [ i ] ;
c. 如果 c > 0 ,并且最后⼀张⽤ 3 卡⽚,最⼤分数为: f [ a ][ b ][ c − 1][ d ] + nums [ i ] ;
d. 如果 d > 0 ,并且最后⼀张⽤ 4 卡⽚,最⼤分数为: f [ a ][ b ][ c ][ d − 1] + nums [ i ] ;
综上所述,取四种情况⾥⾯的最⼤值即可。 - 初始化:
⼀张卡⽚也不⽤的情况下,可以获得第⼀个格⼦的分数, f [0][0][0][0] = nums [1] 。 - 填表顺序:
从⼩到⼤枚举每种卡⽚使⽤的张数即可。
【参考代码】
cpp
#include <iostream>
using namespace std;
const int N = 360, M = 50; // 行1:定义常量,N存格子数(最大350),M存每种卡片最多40张
int n, m; // 行2:n=格子数,m=卡片总数
int x[N], cnt[5]; // 行3:x[N]存每个格子的分数;cnt[5]统计1-4卡片的数量(cnt[1]是1的张数)
int f[M][M][M][M]; // 行4:四维数组,f[a][b][c][d]记用a张1、b张2、c张3、d张4的最大分数
int main() // 行5:程序入口
{
cin >> n >> m; // 行6:输入n(格子数)、m(卡片数)
for(int i = 1; i <= n; i++) cin >> x[i]; // 行7:输入每个格子的分数,x[1]是第1格,x[9]是第9格
for(int i = 1; i <= m; i++) // 行8:循环输入m张卡片
{
int t; cin >> t; // 行9:输入一张卡片的数字(1/2/3/4)
cnt[t]++; // 行10:对应卡片的数量加1(比如t=1,cnt[1]就多1)
}
// 初始化:一张卡片都不用,分数是第1格的分数
f[0][0][0][0] = x[1]; // 行13
// 四层循环:枚举a(1的张数)、b(2的张数)、c(3的张数)、d(4的张数)
for(int a = 0; a <= cnt[1]; a++) // 行15:a从0到cnt[1](比如示例cnt[1]=3,a=0/1/2/3)
for(int b = 0; b <= cnt[2]; b++) // 行16:b从0到cnt[2](示例cnt[2]=1,b=0/1)
for(int c = 0; c <= cnt[3]; c++) // 行17:c从0到cnt[3](示例cnt[3]=1,c=0/1)
for(int d = 0; d <= cnt[4]; d++) // 行18:d从0到cnt[4](示例cnt[4]=0,d=0)
{
// 计算当前用了a/b/c/d张卡片后,棋子的位置
int i = 1 + a + 2 * b + 3 * c + 4 * d; // 行20
// 取f[a][b][c][d]的引用,方便后续修改(不用每次写f[a][b][c][d])
int& t = f[a][b][c][d]; // 行21
// 情况1:最后一步用了1卡片(a>0才有可能)
if(a) t = max(t, f[a - 1][b][c][d] + x[i]); // 行23
// 情况2:最后一步用了2卡片(b>0才有可能)
if(b) t = max(t, f[a][b - 1][c][d] + x[i]); // 行24
// 情况3:最后一步用了3卡片(c>0才有可能)
if(c) t = max(t, f[a][b][c - 1][d] + x[i]); // 行25
// 情况4:最后一步用了4卡片(d>0才有可能)
if(d) t = max(t, f[a][b][c][d - 1] + x[i]); // 行26
}
// 输出用完所有卡片(cnt[1]/cnt[2]/cnt[3]/cnt[4])时的最大分数
cout << f[cnt[1]][cnt[2]][cnt[3]][cnt[4]] << endl; // 行28
return 0; // 行29:程序结束
}