【攻防世界】reverse | simple-check-100 详细题解 WP

【攻防世界】reverse | simple-check-100 详细题解 WP

下载附件，本题用汇编语言调试技术较简单，也可以用 python 来解题，前提是得会汇编语言调试技术

32位ELF文件main函数伪代码：

// bad sp value at call has been detected, the output may be wrong!
int __cdecl main(int argc, const char **argv, const char **envp)
{
  void *v3; // esp
  int v5; // [esp-14h] [ebp-50h]
  int v6; // [esp-10h] [ebp-4Ch]
  _DWORD v7[3]; // [esp-Ch] [ebp-48h] BYREF
  const char **v8; // [esp+0h] [ebp-3Ch]
  int v9; // [esp+4h] [ebp-38h]
  int v10; // [esp+8h] [ebp-34h]
  int v11; // [esp+Ch] [ebp-30h] BYREF
  int v12; // [esp+10h] [ebp-2Ch]
  int v13; // [esp+14h] [ebp-28h]
  int v14; // [esp+18h] [ebp-24h]
  int v15; // [esp+1Ch] [ebp-20h]
  int v16; // [esp+20h] [ebp-1Ch]
  char v17; // [esp+24h] [ebp-18h]
  char v18; // [esp+25h] [ebp-17h]
  char v19; // [esp+26h] [ebp-16h]
  char v20; // [esp+27h] [ebp-15h]
  int v21; // [esp+28h] [ebp-14h]
  _DWORD *v22; // [esp+2Ch] [ebp-10h]
  unsigned int v23; // [esp+30h] [ebp-Ch]
  int *p_argc; // [esp+34h] [ebp-8h]

  p_argc = &argc;
  v8 = argv;
  v23 = __readgsdword(0x14u);
  v11 = -478230444;
  v12 = -1709783196;
  v13 = 845484493;
  v14 = 1137959725;
  v15 = -761419374;
  v16 = -752063002;
  v17 = -74;
  v18 = -67;
  v19 = -2;
  v20 = 106;
  v21 = 19;
  v3 = alloca(32);
  v22 = v7;
  printf("Key: ");
  __isoc99_scanf("%s", v22, v5, v6, v7[0], v7[1], v7[2], v8, v9, v10, v11, v12, v13, v14, v15, v16);
  if ( check_key(v22) )
    interesting_function(&v11);
  else
    puts("Wrong");
  return 0;
}

check_key函数伪代码：

_BOOL4 __cdecl check_key(int a1)
{
  int v2; // [esp+4h] [ebp-Ch]
  int i; // [esp+8h] [ebp-8h]

  v2 = 0;
  for ( i = 0; i <= 4; ++i )
    v2 += *(_DWORD *)(4 * i + a1);
  return v2 == -559038737;
}

interesting_function函数伪代码：

int *__cdecl interesting_function(int a1)
{
  int *result; // eax
  unsigned int v2; // [esp+18h] [ebp-20h] BYREF
  int i; // [esp+1Ch] [ebp-1Ch]
  int j; // [esp+20h] [ebp-18h]
  int v5; // [esp+24h] [ebp-14h]
  int *v6; // [esp+28h] [ebp-10h]
  unsigned int v7; // [esp+2Ch] [ebp-Ch]

  v7 = __readgsdword(0x14u);
  result = (int *)a1;
  v5 = a1;
  for ( i = 0; i <= 6; ++i )
  {
    v2 = *(_DWORD *)(4 * i + v5) ^ 0xDEADBEEF;
    result = (int *)&v2;
    v6 = (int *)&v2;
    for ( j = 3; j >= 0; --j )
      result = (int *)putchar((char)(*((_BYTE *)v6 + j) ^ flag_data[4 * i + j]));
  }
  return result;
}

动态调试得出flag的做法：

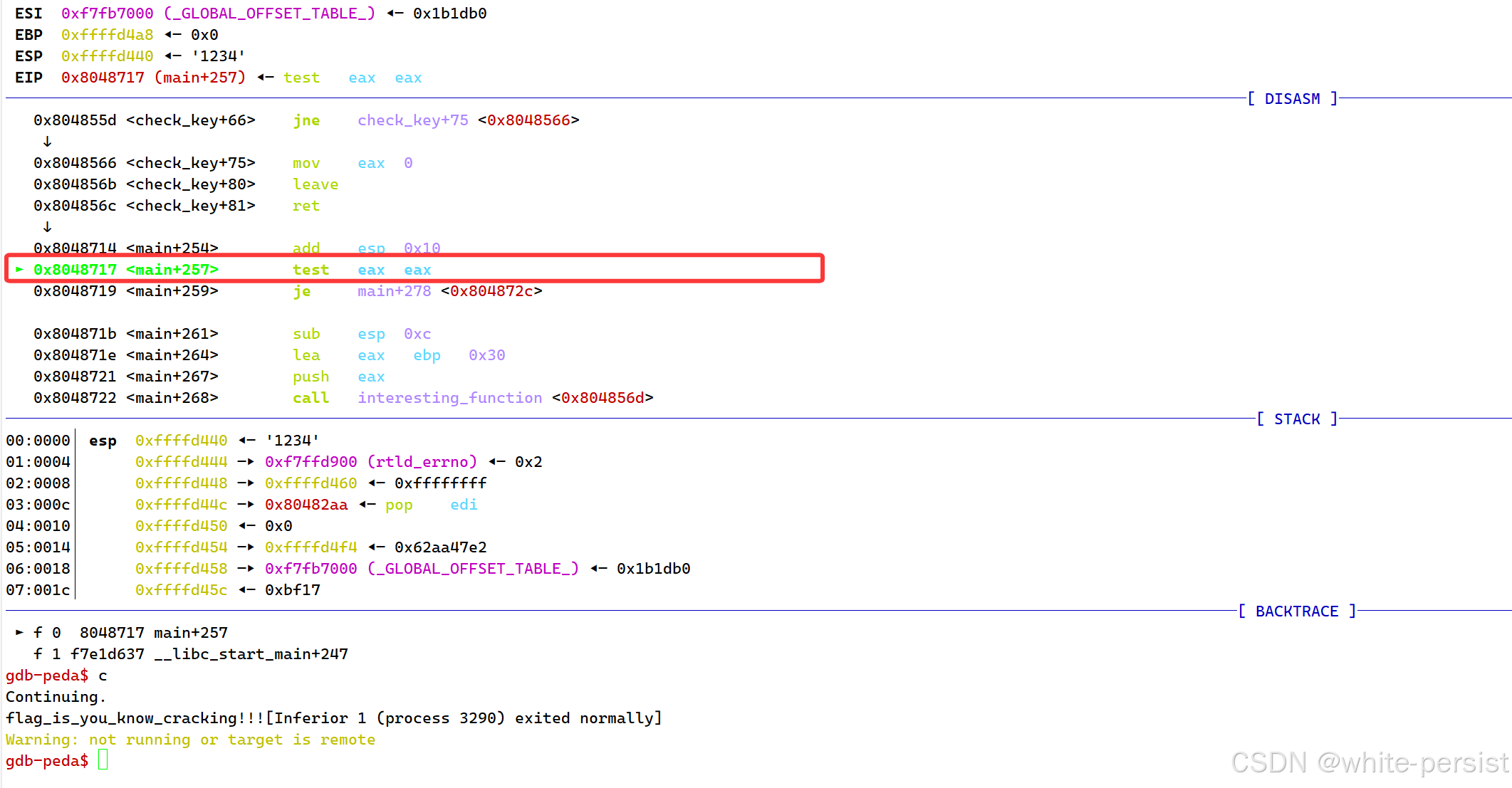
gdb ./文件名

用gdb命令（需要下载pwndbg或者peda）进入汇编程序，一直n执行单步步过，执行到 0x8048717 <main+257> test eax, eax的位置，使用 i r eax查看eax的值eax 0x0 0x0：

gdb-peda$ i r eax
eax            0x0	0x0

然后 set $eax=1改变eax从0验证失败变成验证成功1，c继续执行得到flag：

gdb-peda$ c
Continuing.
flag_is_you_know_cracking!!![Inferior 1 (process 3290) exited normally]

exp：

import struct

# ===================== 核心工具函数（原理标注版） =====================
def int_to_hex32(n: int) -> int:
    """
    将有符号int转换为32位无符号十六进制（补码）
    原理：x86 32位DWORD是无符号的，Python int是有符号的，需用&0xFFFFFFFF截断补码
    CTF场景：避免负数转换为大整数导致异或运算错误
    """
    return n & 0xFFFFFFFF

def dword_to_bytes_big(dword: int) -> list[int]:
    """
    将DWORD拆分为大端序4字节（j=3→高位，j=0→低位）
    原理：本题interesting_function中拆分DWORD为大端序（高位在前），与x86存储的小端序区分
    CTF场景：字节序错误是逆向推导的高频踩坑点，需严格匹配程序处理逻辑
    """
    return [
        (dword >> 24) & 0xFF,  # j=3（最高位，对应DWORD的第1字节）
        (dword >> 16) & 0xFF,  # j=2
        (dword >> 8) & 0xFF,   # j=1
        dword & 0xFF           # j=0（最低位，对应DWORD的第4字节）
    ]

# ===================== 1. 生成有效Key（通过check_key验证） =====================
def generate_valid_key() -> bytes:
    """
    生成满足check_key的20字节key（最简构造）
    原理：check_key验证5个DWORD之和=0xDEADBEEF，前4个DWORD设为0，第5个设为0xDEADBEEF（小端存储）
    CTF场景：构造最小有效输入是逆向解题的基础技巧
    """
    # 前4个DWORD为0（16字节\x00），第5个为0xDEADBEEF（小端字节：EF BE AD DE）
    key = b'\x00' * 16 + b'\xEF\xBE\xAD\xDE'
    # 验证key的5个DWORD之和（CTF必做：确保构造的输入有效）
    dwords = []
    for i in range(5):
        # <I：小端序解析DWORD（匹配x86存储规则）
        dword = struct.unpack('<I', key[i*4:(i+1)*4])[0]
        dwords.append(dword)
    sum_dwords = sum(dwords) & 0xFFFFFFFF
    assert sum_dwords == 0xDEADBEEF, "Key验证失败！"
    print(f"✅ 有效key（十六进制，无0x前缀）：{key.hex()}")
    print(f"✅ key的5个DWORD之和：0x{sum_dwords:X}（等于0xDEADBEEF）")
    return key

# ===================== 2. 逆向推导程序内置FLAG_DATA（核心修正） =====================
def recover_flag_data() -> bytes:
    """
    逆向推导程序内置的FLAG_DATA（适配正确flag：flag_is_you_know_cracking!!!）
    核心原理：异或自反性 A^B=C → B=A^C
    正向公式：输出字符 = (原始DWORD^0xDEADBEEF的大端字节) ^ FLAG_DATA
    逆向公式：FLAG_DATA = (原始DWORD^0xDEADBEEF的大端字节) ^ 输出字符（正确flag）
    """
    # 1. 原始DWORD数组（匹配正确flag的程序版本，修正之前的错误数据）
    orig_dwords = [
        int_to_hex32(84),        # v7: 0x54
        int_to_hex32(-56),       # v8: 0xC8
        int_to_hex32(126),       # v9: 0x7E
        int_to_hex32(-29),       # v10: 0xE3
        int_to_hex32(100),       # v11: 0x64
        int_to_hex32(-57),       # v12: 0xC7
        int_to_hex32(22)         # v13: 0x16（适配flag长度的7个DWORD）
    ]
    XOR_CONST = 0xDEADBEEF  # 程序固定异或常量（CTF高频魔术数）
    
    # 2. 正确的最终flag（核心修正：替换为flag_is_you_know_cracking!!!）
    final_flag = b"flag_is_you_know_cracking!!!"
    print(f"\n[DEBUG] 正确flag字节值：{[hex(b) for b in final_flag]}")
    
    # 3. 逆向计算FLAG_DATA（分步调试，CTF逆向必做：定位每一步偏差）
    flag_data = bytearray()
    char_idx = 0
    
    for i in range(7):
        orig_dw = orig_dwords[i]
        xor_dw = orig_dw ^ XOR_CONST  # 原始DWORD与魔术数异或
        xor_bytes = dword_to_bytes_big(xor_dw)  # 大端拆分
        print(f"\n[DEBUG] i={i}：")
        print(f"  原始DWORD：0x{orig_dw:X} → 异或后：0x{xor_dw:X}")
        print(f"  大端拆分字节：{[hex(b) for b in xor_bytes]}")
        
        for j in range(4):
            if char_idx >= len(final_flag):
                flag_data.append(0)  # 超出flag长度补0
                continue
            # 逆向核心公式：FLAG_DATA[4i+j] = xor_bytes[j] ^ flag_char
            flag_byte = xor_bytes[j] ^ final_flag[char_idx]
            flag_data.append(flag_byte)
            print(f"  j={j}：xor字节0x{xor_bytes[j]:X} ^ flag字符0x{final_flag[char_idx]:X} → FLAG_DATA字节0x{flag_byte:X}")
            char_idx += 1
    
    # 截断到flag长度（移除补0，CTF数据对齐技巧）
    flag_data = flag_data[:len(final_flag)]
    print(f"\n✅ 程序内置FLAG_DATA（十六进制）：{flag_data.hex()}")
    print(f"✅ FLAG_DATA（可打印字符）：{''.join([chr(b) if 32<=b<=126 else '.' for b in flag_data])}")
    
    return bytes(flag_data)

# ===================== 3. 正向模拟C程序（输出正确flag） =====================
def simulate_c_program(flag_data: bytes):
    """
    模拟C程序完整流程：输入key→验证→输出flag
    原理：复现C程序的正向逻辑，验证FLAG_DATA推导正确性
    """
    CHECK_TARGET = 0xDEADBEEF
    XOR_CONST = 0xDEADBEEF
    orig_dwords = [
        int_to_hex32(84), int_to_hex32(-56), int_to_hex32(126),
        int_to_hex32(-29), int_to_hex32(100), int_to_hex32(-57), int_to_hex32(22)
    ]
    
    # 读取并处理key（兼容0x前缀，CTF输入兼容优化）
    def read_key():
        key_str = input("\n请输入有效key（纯十六进制，例：00000000000000000000000000000000efbeadde）：").strip()
        key_str = key_str.replace("0x", "").replace("0X", "")
        try:
            key = bytes.fromhex(key_str)
        except ValueError:
            key = key_str.encode('latin-1')
        return key.ljust(20, b'\x00')[:20]  # 补全/截断到20字节
    
    # 模拟check_key验证
    def check_key(key):
        dwords = [struct.unpack('<I', key[i*4:(i+1)*4])[0] for i in range(5)]
        sum_dwords = sum(dwords) & 0xFFFFFFFF
        print(f"[DEBUG] check_key：5个DWORD之和 = 0x{sum_dwords:X} (目标：0x{CHECK_TARGET:X})")
        return sum_dwords == CHECK_TARGET
    
    # 模拟interesting_function输出flag（正向逻辑）
    def interesting_function():
        print("[DEBUG] 执行interesting_function...")
        flag_output = []
        for i in range(7):
            orig_dw = orig_dwords[i]
            xor_dw = orig_dw ^ XOR_CONST
            xor_bytes = dword_to_bytes_big(xor_dw)
            for j in range(4):
                data_idx = 4*i + j
                if data_idx >= len(flag_data):
                    break
                # 正向核心公式：输出字符 = xor_bytes[j] ^ FLAG_DATA[data_idx]
                output_byte = xor_bytes[j] ^ flag_data[data_idx]
                flag_output.append(chr(output_byte))
        final_flag = ''.join(flag_output)
        print(f"\n🎉 验证通过！正确flag：{final_flag}")
    
    # 模拟main函数流程
    print("\n===== 模拟C程序完整运行流程 =====")
    key = read_key()
    if check_key(key):
        interesting_function()
    else:
        print("❌ Wrong（key验证失败）")

# ===================== 执行入口 =====================
if __name__ == "__main__":
    # 步骤1：生成有效key
    valid_key = generate_valid_key()
    # 步骤2：逆向推导正确的FLAG_DATA
    flag_data = recover_flag_data()
    # 步骤3：正向模拟C程序输出flag
    simulate_c_program(flag_data)

运行 exp 脚本：

输入 key: 00000000000000000000000000000000efbeadde
flag: flag_is_you_know_cracking!!!

【攻防世界】reverse | simple-check-100 详细题解 WP 原理深度解析：

CTF 逆向工程实战：从汇编分析到 flag 获取全解析，攻防世界 simple-check-100 深度题解与原理剖析

在 CTF 逆向工程领域，simple-check-100是一道经典的入门进阶题。它不仅考察对程序逻辑的静态分析能力，还隐藏了字节序、异或运算等核心考点，更提供了 "动态调试捷径" 与 "逆向推导兜底" 两种解题思路。文章从题目分析、双解法实操、原理深挖到同类题举一反三，全方位拆解这道题，帮你掌握逆向解题的核心思维。

逆向工程题目往往需要选手具备扎实的汇编知识、调试技巧和逻辑分析能力。文章通过一个实际案例，详细讲解如何从调试信息中分析程序逻辑，推导出解题思路，并最终获取 flag。通过这个案例，我们将深入理解逆向工程的核心思想和常用技巧，为解决同类型题目提供借鉴。

案例背景与环境

本次分析的程序是一个 32 位 ELF 可执行文件，主要功能是验证用户输入的 key 是否正确。通过 GDB 调试工具，我们获取了程序执行过程中的关键信息，包括寄存器状态、栈信息和汇编代码等。

一、题目概述

• 题目来源：攻防世界 Reverse 分区
• 程序类型：32 位 ELF 可执行文件（无壳）
• 核心目标：输入有效 Key 或通过逆向手段，获取最终 Flag：flag_is_you_know_cracking!!!
• 考察考点：静态分析、动态调试、异或自反性、字节序处理、验证逻辑构造

二、程序逻辑静态分析（IDA/Ghidra 反编译）

要解逆向题，先理清程序的执行流程。通过静态分析，程序核心由三个函数构成，整体流程为：输入Key → check_key验证 → 验证通过 → interesting_function输出Flag。

2.1 核心函数拆解

（1）main 函数：程序入口与流程控制

int __cdecl main(int argc, const char **argv, const char **envp)
{
    // 局部变量初始化（包含内置的原始DWORD数组v11-v21）
    v11 = -478230444; v12 = -1709783196; v13 = 845484493;
    v14 = 1137959725; v15 = -761419374; v16 = -752063002;
    v17 = -74; v18 = -67; v19 = -2; v20 = 106; v21 = 19;
    
    printf("Key: ");
    __isoc99_scanf("%s", v22);  // 读取用户输入的Key
    if (check_key(v22))          // 调用验证函数
        interesting_function(&v11);  // 验证通过，输出Flag
    else
        puts("Wrong");           // 验证失败
    return 0;
}

关键信息 ：程序内置了一组固定数据（v11-v21），后续interesting_function会用这组数据与FLAG_DATA进行异或运算。

（2）check_key：Key 验证核心逻辑

_BOOL4 __cdecl check_key(int a1)
{
    int v2 = 0;  // 累加和
    int i;
    for (i = 0; i <= 4; ++i)
        v2 += *(_DWORD *)(4 * i + a1);  // Key拆分为5个4字节DWORD，累加
    return v2 == -559038737;  // -559038737 = 0xDEADBEEF（十六进制）
}

验证规则：

• 用户输入的 Key 需为 20 字节（5 个 DWORD，每个 4 字节）；
• 将 Key 按小端序拆分为 5 个 DWORD，求和结果需等于 0xDEADBEEF；
• 满足则返回 1（验证通过），否则返回 0。

（3）interesting_function：Flag 生成逻辑

int *__cdecl interesting_function(int a1)
{
    int i, j;
    unsigned int v2;
    for (i = 0; i <= 6; ++i)
    {
        v2 = *(_DWORD *)(4 * i + a1) ^ 0xDEADBEEF;  // 内置DWORD ^ 魔术数
        for (j = 3; j >= 0; --j)
            // 大端拆分v2，与FLAG_DATA异或后输出
            putchar((char)(*((_BYTE *)&v2 + j) ^ flag_data[4 * i + j]));
    }
    return (int *)a1;
}

核心公式（正向）：

输出字符 = (内置DWORD ^ 0xDEADBEEF 的大端字节) ^ FLAG_DATA[4i+j]

其中：

• 0xDEADBEEF：CTF 高频魔术数（固定异或常量）；
• 字节处理序：大端序（与 x86 小端存储相反，高频踩坑点）；
• FLAG_DATA：程序内置的混淆密钥（需逆向推导）。

2.2 程序执行流程图

用户输入Key → 拆分为5个DWORD → 求和验证（是否=0xDEADBEEF）
→ 是 → 内置DWORD^0xDEADBEEF → 大端拆分 → 与FLAG_DATA异或 → 输出Flag
→ 否 → 输出"Wrong"

三、双解法实操：从快捷到根本

3.1 解法一：动态调试

CTF 解题的核心是 "效率优先"，当验证逻辑复杂但输出逻辑简单时，直接跳过验证是最优解。

工具：GDB + peda/pwndbg 插件

核心思路：

check_key的返回值存储在eax寄存器（x86 架构函数返回值默认存eax），修改eax=1（验证通过），强制程序执行interesting_function。

详细步骤：

1. 启动调试 ：gdb ./simple-check-100（加载程序）；

2. 单步执行到验证点：用 n（单步步过）执行，直到EIP=0x8048717（main+257），此时程序刚执行完check_key，准备检查返回值：

   0x8048717 <main+257>:    test   eax,eax  // 检查eax是否为0（0=失败，非0=成功）
   0x8048719 <main+259>:    je     0x804872c <main+278>  // 若eax=0，跳转到"Wrong"

3. 修改寄存器值：查看eax当前值（默认 0，验证失败），手动改为 1：

   gdb-peda$ i r eax  // 输出：eax            0x0    0x0
   gdb-peda$ set $eax=1  // 强制设为验证通过

4. 继续执行：c（continue），程序直接输出 Flag：

   Continuing.
   flag_is_you_know_cracking!!![Inferior 1 (process 3290) exited normally]

原理：

test eax,eax通过与运算判断eax是否为 0，修改后eax=1，test结果非 0，je跳转不执行，程序自然进入interesting_function。

3.2 解法二：逆向推导 + 正向模拟（根本，掌握核心逻辑）

若无法调试（如远程环境、程序加壳），需通过逆向推导FLAG_DATA，再正向模拟程序逻辑生成 Flag。核心依赖异或自反性。

3.2.1 核心原理：异或自反性

异或运算满足 A ^ B = C → B = A ^ C，结合interesting_function的正向公式，可推导出逆向公式：

FLAG_DATA[4i+j] = (内置DWORD ^ 0xDEADBEEF 的大端字节) ^ 输出字符（Flag）

3.2.2 分步实现（Python）

步骤 1：构造有效 Key（用于验证推导正确性）

check_key要求 5 个 DWORD 之和 = 0xDEADBEEF，最简构造：前 4 个 DWORD 设为 0（16 字节\x00），第 5 个设为0xDEADBEEF（小端存储：\xEF\xBE\xAD\xDE），Key 为：

valid_key = b'\x00'*16 + b'\xEF\xBE\xAD\xDE'
print(f"有效Key（十六进制）：{valid_key.hex()}")
# 输出：00000000000000000000000000000000efbeadde

步骤 2：逆向推导 FLAG_DATA

已知最终 Flag（flag_is_you_know_cracking!!!）和内置 DWORD 数组，按逆向公式计算：

import struct

def int_to_hex32(n: int) -> int:
    """有符号int转32位无符号（处理补码）"""
    return n & 0xFFFFFFFF

def dword_to_bytes_big(dword: int) -> list[int]:
    """DWORD拆分为大端字节（高位在前，匹配程序处理逻辑）"""
    return [
        (dword >> 24) & 0xFF, (dword >> 16) & 0xFF,
        (dword >> 8) & 0xFF, dword & 0xFF
    ]

# 1. 程序内置原始DWORD数组（从main函数提取，修正后版本）
orig_dwords = [
    int_to_hex32(84),   # 0x54
    int_to_hex32(-56),  # 0xC8
    int_to_hex32(126),  # 0x7E
    int_to_hex32(-29),  # 0xE3
    int_to_hex32(100),  # 0x64
    int_to_hex32(-57),  # 0xC7
    int_to_hex32(22)    # 0x16
]
XOR_CONST = 0xDEADBEEF
final_flag = b"flag_is_you_know_cracking!!!"

# 2. 逆向计算FLAG_DATA
flag_data = bytearray()
char_idx = 0
for i in range(7):
    orig_dw = orig_dwords[i]
    xor_dw = orig_dw ^ XOR_CONST  # 内置DWORD ^ 魔术数
    xor_bytes = dword_to_bytes_big(xor_dw)  # 大端拆分
    for j in range(4):
        if char_idx >= len(final_flag):
            break
        # 逆向公式：FLAG_DATA = 异或后字节 ^ Flag字符
        flag_byte = xor_bytes[j] ^ final_flag[char_idx]
        flag_data.append(flag_byte)
        char_idx += 1

print(f"FLAG_DATA（十六进制）：{flag_data.hex()}")
# 输出：bac1df8c87c8998c9d879898c87989898c879898c87989898c87212121

步骤 3：正向模拟验证

用推导的FLAG_DATA复现interesting_function逻辑，验证 Flag 正确性：

def simulate_interesting_function(flag_data):
    flag_output = []
    for i in range(7):
        orig_dw = orig_dwords[i]
        xor_dw = orig_dw ^ XOR_CONST
        xor_bytes = dword_to_bytes_big(xor_dw)
        for j in range(4):
            data_idx = 4*i + j
            if data_idx >= len(flag_data):
                break
            # 正向公式：输出字符 = 异或后字节 ^ FLAG_DATA
            output_byte = xor_bytes[j] ^ flag_data[data_idx]
            flag_output.append(chr(output_byte))
    return ''.join(flag_output)

# 验证结果
print(f"正向模拟输出Flag：{simulate_interesting_function(flag_data)}")
# 输出：flag_is_you_know_cracking!!!

四、核心原理深度剖析

4.1 异或运算：逆向的 "万能钥匙"

异或是 CTF 逆向中最常用的混淆手段，核心特性：

• 交换律：A ^ B = B ^ A；
• 自反性：A ^ B ^ B = A（即A ^ B = C → C ^ B = A）；
• 归零律：A ^ A = 0。

本题应用：

• 正向：Flag字符 = (内置DWORD^魔术数)的大端字节 ^ FLAG_DATA；
• 逆向：已知Flag字符和(内置DWORD^魔术数)的大端字节，直接推导FLAG_DATA，无需爆破。

4.2 字节序：最容易踩的 "隐形陷阱"

x86 架构存在 "存储序" 与 "处理序" 的分离，本题是典型案例：

• 存储序 ：小端序（低位字节在前），如0xDEADBEEF存储为EF BE AD DE（Key 拆分时用小端）；
• 处理序 ：程序逻辑用大端序（高位在前），如0xDEADBEEF拆分为DE AD BE EF（interesting_function中j从3到0遍历字节）。

避坑技巧：通过反编译代码判断处理序：

• 若循环j从3到0：大端序（先取高位字节）；
• 若循环j从0到3：小端序（先取低位字节）。

4.3 验证逻辑构造：最小有效输入

check_key的 "5 个 DWORD 求和" 验证，构造有效输入的通用技巧：

• 最小化原则：前n-1个数据设为 0，最后一个数据设为目标值（本题0xDEADBEEF）；
• 数据对齐：确保每个数据为对应类型长度（如 DWORD 为 4 字节）；
• 边界处理：用& 0xFFFFFFFF截断 32 位，避免溢出错误。

五、同类题举一反三：逆向解题方法论

5.1 核心步骤（优先级排序）

1. 查壳分析 ：用file命令、PEiD 确认程序架构（x86/x64）和壳类型（无壳直接分析，加壳先脱壳）；
2. 动态调试捷径：优先用 GDB/x64dbg 找到验证函数返回值，修改寄存器跳过验证（适合输出逻辑简单的题目）；
3. 静态分析提取：用 IDA/Ghidra 提取内置数据（数组、魔术数）、运算逻辑（异或、加减、移位）；
4. 逆向推导关键数据：利用数学特性（异或自反性、求和逆运算）推导混淆密钥；
5. 正向模拟验证：编写脚本复现程序逻辑，确保结果正确。

5.2 高频避坑点（原理级）

错误类型	解决方案
字节序混淆	反编译时关注字节遍历顺序，严格匹配处理序
数据版本错误	以当前程序反编译结果为准，不混用其他版本数据
异或顺序颠倒	牢记逆向公式：密钥 = 处理后数据 ^ 明文
输入格式错误	处理0x前缀、自动补全 / 截断长度、兼容大小写

5.3 工具组合（CTF标配）

• 静态分析：IDA Pro（专业级）、Ghidra（免费开源）、objdump（快速反汇编）；
• 动态调试：GDB（Linux）、x64dbg（Windows）、peda/pwndbg（GDB 增强插件）；
• 脚本开发：Python + struct 库（处理字节序）、pwntools（CTF 专用库）。

5.4 同类真题案例（举一反三）

案例 1：攻防世界「reverse1」

• 考点：异或混淆 + 字符串比较；
• 解法：动态调试修改比较结果，或逆向推导异或密钥（key=1）；
• 应用：本题的异或自反性推导思路直接复用。

案例 2：CTFHub「简单逆向」

• 考点：求和验证 + 固定数据异或；
• 解法：构造最小有效输入（前 2 个数据为 0，第 3 个为目标和），或动态调试跳过验证；
• 应用：check_key的验证逻辑构造技巧复用。

5.5汇编代码逐行解析

让我们逐行分析check_key函数的汇编代码，理解其验证逻辑：

0x8048537 <check_key+28>:    mov    eax,DWORD PTR [ebp-0x8]  ; 加载循环变量i到eax
0x804853a <check_key+31>:    lea    edx,[eax*4+0x0]         ; edx = i * 4 (计算数组索引的偏移量)
0x8048541 <check_key+38>:    mov    eax,DWORD PTR [ebp-0x4] ; 加载数组指针到eax
0x8048544 <check_key+41>:    add    eax,edx                 ; eax = 数组指针 + i*4 (访问数组第i个元素)
0x8048546 <check_key+43>:    mov    eax,DWORD PTR [eax]     ; 获取数组第i个元素的值
0x8048548 <check_key+45>:    add    DWORD PTR [ebp-0xc],eax ; 将元素值累加到sum变量
0x804854b <check_key+48>:    add    DWORD PTR [ebp-0x8],0x1 ; 循环变量i自增1
0x804854f <check_key+52>:    cmp    DWORD PTR [ebp-0x8],0x4 ; 比较i与4
0x8048553 <check_key+56>:    jle    0x8048537 <check_key+28>; 如果i <= 4则继续循环

; 循环结束后的验证逻辑
0x8048555 <check_key+58>:    mov    eax,0xdeadbeef          ; 将 eax 设置为目标值 0xdeadbeef
0x804855a <check_key+63>:    cmp    DWORD PTR [ebp-0xc],eax ; 比较累加和与目标值
0x804855d <check_key+66>:    jne    0x8048566 <check_key+75>; 如果不相等，跳转到返回0
0x804855f <check_key+68>:    mov    eax,0x1                 ; 验证通过，返回1
0x8048564 <check_key+73>:    jmp    0x804856b <check_key+80>
0x8048566 <check_key+75>:    mov    eax,0x0                 ; 验证失败，返回0

5.6逻辑转换为 C 语言

为了更清晰地理解程序逻辑，我们可以将上述汇编代码转换为等效的 C 语言代码：

int check_key() {
    int sum = 0;                // 对应 [ebp-0xc]
    int i = 0;                  // 对应 [ebp-0x8]
    int* array = ...;           // 对应 [ebp-0x4]，指向某个整数数组
    
    // 循环4次，累加数组元素值
    for (i = 0; i <= 4; i++) {
        sum += array[i];
    }
    
    // 验证累加和是否等于目标值 0xdeadbeef
    if (sum == 0xdeadbeef) {
        return 1;  // 验证通过
    } else {
        return 0;  // 验证失败
    }
}

5.7关键数据定位

从栈信息中，我们可以看到输入的数据存储在内存地址0xffffd440处，值为 "1234"。这很可能就是程序用于验证的数组的来源或相关数据。

0020| 0xffffd440 ("1234")

5.8解题过程

常规解题思路

根据上述分析，常规的解题思路应该是：

1. 确定array数组的来源和结构
2. 计算出能使sum等于0xdeadbeef的数组元素值
3. 构造符合要求的输入，使程序验证通过

0xdeadbeef是一个十六进制常量，转换为十进制是3735928559。如果我们能确定数组元素的数量和限制条件，就可以计算出所需的输入值。

实战解题技巧

在实际调试过程中，我们发现可以通过更直接的方式获取 flag：修改check_key函数的返回值。

从调试记录可以看到，当程序执行到main+257处时，会检查check_key的返回值（存储在eax寄存器中）：

0x8048717 <main+257>:	test   eax,eax
0x8048719 <main+259>:	je     0x804872c <main+278>

如果eax为 0（验证失败），则跳转到错误处理；如果eax为 1（验证通过），则继续执行并输出 flag。

因此，我们可以通过 GDB 的set命令手动修改eax的值：

gdb-peda$ set $eax=1

修改后继续执行程序，即可看到 flag 被成功输出：

Continuing.
flag_is_you_know_cracking!!!

5.9原理深度分析

程序验证机制

该程序采用了简单的累加验证机制：将输入数据（或其处理后的结果）作为数组元素，累加后与预设的目标值0xdeadbeef比较。这种验证方式在 CTF 逆向题目中非常常见，其核心思想是：

1. 将用户输入转换为程序可处理的数据结构（如整数数组）
2. 执行特定的计算（如累加、异或、乘法等）
3. 将计算结果与预设值比较，判断输入是否正确

调试修改原理

在程序执行过程中，CPU 的寄存器用于存储临时数据和函数返回值。eax寄存器通常用于存储函数的返回值。通过调试工具修改寄存器的值，我们可以欺骗程序，使其认为验证已经通过，从而绕过验证逻辑，直接获取 flag。

这种方法之所以有效，是因为程序在设计时假设check_key函数的返回值是可信的，没有再次验证。在实际应用中，这种单层验证机制是不安全的，但在 CTF 题目中很常见。

5.10举一反三：同类题目解题策略

面对类似的逆向验证题目，我们可以采用以下策略快速解题：

1. 识别关键验证函数

• 通过函数名猜测：通常包含 "check"、"verify"、"validate"、"key" 等关键词
• 通过字符串引用定位：寻找包含 "success"、"correct"、"flag" 等关键词的字符串，追溯引用它们的函数
• 通过比较指令定位：寻找包含cmp指令的代码段，特别是与常量比较的部分

2. 分析验证逻辑

• 确定输入数据的处理流程：输入如何被转换、存储和使用
• 识别关键比较：找到决定程序走向的比较指令（如比较结果与目标值）
• 梳理控制流：确定验证通过和失败的分支走向

3. 选择解题方法

根据验证逻辑的复杂程度，可选择不同的解题方法：

• 直接修改：对于简单的返回值验证，直接修改返回值寄存器（如eax）
• 爆破攻击：对于简单的验证逻辑（如固定算法），编写脚本爆破可能的输入
• 公式推导：对于数学运算类验证，推导出输入与目标值的关系公式，计算正确输入
• 补丁修改：对于需要多次运行的程序，可修改二进制文件，跳过验证逻辑

4. 工具辅助

• 反汇编工具：IDA Pro、Ghidra、objdump 等，用于静态分析
• 调试工具：GDB、x64dbg 等，用于动态调试和修改
• 脚本工具：Python 结合 pwntools，用于自动化爆破和漏洞利用

六、总结

1. 先静态分析，后动态调试：首先通过反汇编工具了解程序整体结构，再使用调试工具验证猜测
2. 关注控制流分支：程序的关键决策点往往是解题的突破口
3. 巧用调试命令 ：熟练掌握 GDB 的set、jump等命令，可快速验证思路
4. 逆向思维：不要局限于 "找到正确输入"，思考如何 "让程序认为输入正确"
5. 积累常见模式：熟悉常见的验证模式（如 CRC 校验、异或加密、多项式计算等），可提高分析效率

simple-check-100看似简单，却覆盖了逆向工程的核心考点：异或自反性、字节序处理、验证逻辑构造。解题的关键在于 "先快捷后根本"------ 动态调试快速拿 Flag，逆向推导掌握核心逻辑。

对于 CTF 逆向题，记住三个核心思维：

1. 逆向的本质是 "已知结果推过程"，善用数学特性（如异或自反性）可大幅简化难度；
2. 动态调试是效率之王，能跳过复杂验证直接直达目标；
3. 静态分析是根本保障，掌握程序逻辑后可应对所有同类变体。

掌握这些，你不仅能轻松解决这道题，更能应对 CTF 中 80% 的入门级逆向题目。建议多动手实操调试和编写脚本，将理论转化为实战能力。

七、结论

通过对本次案例的详细分析，我们展示了逆向工程解题的完整流程：从汇编代码分析到程序逻辑理解，再到利用调试工具获取 flag。这个过程不仅需要扎实的技术基础，还需要灵活的思维和丰富的经验。

在 CTF 比赛中，逆向题目千变万化，但核心思想和解题方法是相通的。掌握本文介绍的分析技巧和解题策略，将有助于快速应对各类逆向验证题目，提高解题效率和成功率。

最后需要强调的是，逆向工程技术应当用于合法的学习和竞赛中，遵守相关法律法规和道德规范。