
本文章知识来源于《深度学习入门》 (鱼书),特此声明。可以当做读数笔记来进行阅读。
NumPy
在深度学习的实现中,经常出现数组和矩阵的计算。NumPy的数组类 (numpy.array)中提供了很多便捷的方法,在实现深度学习时,我们将使用这些方法。
核心功能:
- 多维数组对象(ndarray) :所有元素类型相同,由
dtype属性指定,如int32、float64等,通过shape属性表示各维度大小,例如二维数组形状为(行数, 列数)元素在内存中连续存储,便于快速访问和运算 - **高效存储与计算:**基于C语言实现,数组存储紧凑,运算速度远超Python原生列表。支持向量化操作,避免显式循环,大幅提升代码简洁性和执行效率
- **广播机制:**支持不同形状数组间的运算,简化数据处理逻辑
- **丰富的数学函数库:**提供全面的数学函数,包括统计函数、线性代数函数、傅里叶变换等
- **集成性强:**与Pandas、SciPy、Matplotlib等库深度整合,是数据分析和机器学习的基础
shell
pip install numpy
python
import numpy as np
print(np.__version__) # 2.2.6生成数组
python
# 从列表创建一维数组
a = np.array([1, 2, 3, 4, 5])
# [1 2 3 4] type:<class 'numpy.ndarray'>
print(f'{a} type:{type(a)}')
# 从列表创建二维数组
# [[1 2 3]
# [4 5 6]] type:<class 'numpy.ndarray'>
b = np.array([[1, 2, 3], [4, 5, 6]])
print(f'{b} type:{type(b)}')
# 创建全零二维数组
#[[0. 0. 0.]
# [0. 0. 0.]] type:<class 'numpy.ndarray'>
zeros = np.zeros((2, 3))
print(f'{zeros} type:{type(zeros)}')
# 创建全一二维数组
#[[1. 1. 1.]
# [1. 1. 1.]
# [1. 1. 1.]] type:<class 'numpy.ndarray'>
ones = np.ones((3, 3))
print(f'{ones} type:{type(ones)}')
# 创建等差数列
arange = np.arange(start=0, stop=10, step=2)
# [0 2 4 6 8]
print(arange)
# 创建随机数组
rand = np.random.rand(2, 2)
print(rand)算数运算
python
x = np.array([1.0, 2.0, 3.0])
y = np.array([2.0, 4.0, 6.0])
# 如果元素个数不同,程序就会报错
# "对应元素的"的英文是element-wise
x + y # 对应元素的加法 [ 3., 6., 9.]
x - y # [ -1., -2., -3.]
x * y # [ 2., 8., 18.]
x / y # [ 0.5, 0.5, 0.5]
x = np.array([1.0, 2.0, 3.0])
x / 2.0 # [ 0.5, 1. , 1.5] 也叫做广播N维数组
python
A = np.array([[1, 2], [3, 4]])
print(A)
# [[1 2]
# [3 4]]
A.shape # (2,2) 表示两行,两列的矩阵
A.dtype # dtype('int64')和数组的算术运算一样,矩阵的算术运算也可以在相同形状的矩阵间以
对应元素的方式进行。并且,也可以通过标量(单一数值)对矩阵进行算术运算。
这也是基于广播的功能
python
A = np.array([[1, 2], [3, 4]])
B = np.array([[3, 0],[0, 6]])
A+B
# array([[ 4, 2],
# [ 3, 10]])
A*B
# array([[ 3, 0],
# [ 0, 24]])NumPy数组(np.array)可以生成_N_维数组,即可以生成一维数组、
二维数组、三维数组等任意维数的数组。数学上将一维数组称为向量,
将二维数组称为矩阵。另外,可以将一般化之后的向量或矩阵等统
称为张量(tensor)。
广播
NumPy中,形状不同的数组之间也可以进行运算。
python
A = np.array([[1, 2], [3, 4]])
# 2*2 的矩阵A和标量10 做乘法运算
A*10标量10 被扩展成了 2* 2 的形状,然后再与矩阵A进行乘法运算,这个功能称为 广播 (broadcast)

再看一个例子:
python
A = np.array([[1, 2], [3, 4]])
B = np.array([10, 20])
A*B
# array([[ 10, 40],
# [ 30, 80]])
Matplotlib
在深度学习的实验中,图形的绘制和数据的可视化非常重要。Matplotlib是用于绘制图形的库,使用Matplotlib可以轻松地绘制图形和实现数据的可视化。
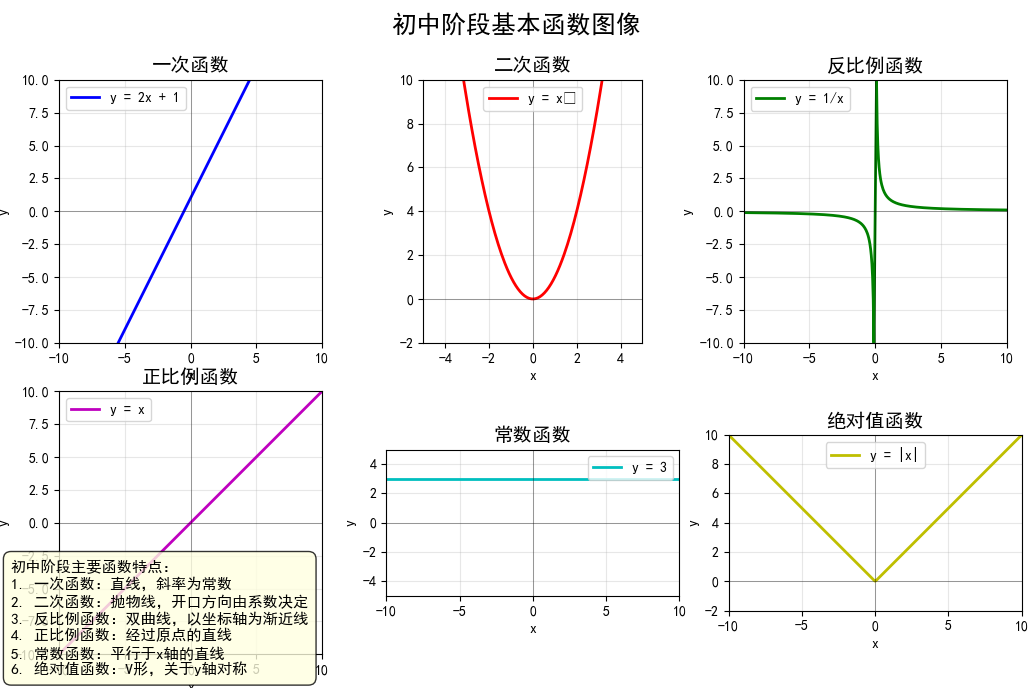
python
"""
全局设置
"""
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
if __name__ == '__main__':
# 创建一个绘图窗口, 宽 15英寸,高 10 英寸
fig = plt.figure(figsize=(15, 10))
# 顶部绘制文字,18号,加粗
fig.suptitle('初中阶段基本函数图像', fontsize=18, fontweight='bold')
# 使用GridSpec创建2x3的子图布局
# 第一行: 一次函数,二次函数, 反比例函数
# 第二行: 正比例函数,常数函数, 绝对值函数
gs = gridspec.GridSpec(2, 3, figure=fig)
# 1. 一次函数 y = 2x + 1
plot_linear_function(gs)
# 2. 二次函数 y = x²
plot_quadratic_function(gs)
# 3. 反比例函数 y = 1/x
plot_inverse_proportion_function(gs)
# 4. 正比例函数 y = x
plot_proportion_function(gs)
# 5. 常数函数 y = 3
plot_constant_function(gs)
# 6. 绝对值函数 y = |x|
plot_absolute_value_function(gs)
# 调整子图间距
# rect=[0, 0, 1, 0.96] 定义了子图布局的矩形区域:
# [左, 下, 右, 上] 分别对应矩形区域的边界
# 0, 0 表示左侧和底部从0开始
# 1, 0.96 表示右侧到1结束,顶部到0.96结束
plt.tight_layout(rect=[0, 0, 1, 0.96])
# 添加函数特点说明
# 坐标(0.02, 0.02)表示文本左下角的位置(相对坐标,0-1之间)
fig.text(0.02, 0.02,
'初中阶段主要函数特点:\n'
'1. 一次函数:直线,斜率为常数\n'
'2. 二次函数:抛物线,开口方向由系数决定\n'
'3. 反比例函数:双曲线,以坐标轴为渐近线\n'
'4. 正比例函数:经过原点的直线\n'
'5. 常数函数:平行于x轴的直线\n'
'6. 绝对值函数:V形,关于y轴对称',
fontsize=11,
bbox=dict(boxstyle="round,pad=0.5", facecolor="lightyellow", alpha=0.8))
plt.show()
python
def plot_linear_function(gs):
"""
绘制一次函数
"""
# 定义x的取值范围
x = np.linspace(-10, 10, 400)
# 1. 一次函数 y = 2x + 1
# gs 是一个 2*3 的布局,
# fig.add_subplot(gs[0, 0]) 表示在 0行 0列 创建一个子图
ax1 = fig.add_subplot(gs[0, 0])
y = 2 * x + 1
# 绘制一次函数图像,plot是: matplotlib中用于绘制线条图的方法
# x: x轴坐标数据(-10到10的400个点)
# y: y轴坐标数据(根据函数y = 2x + 1计算得出)
# 'b-': 绘制样式,b表示蓝色(blue),-表示实线
# linewidth=2: 线条宽度为2个像素
# label='y = 2x + 1': 图例标签,显示函数表达式
ax1.plot(x, y, 'b-', linewidth=2, label='y = 2x + 1')
# 是matplotlib中用于绘制水平线的方法
# y=0: 水平线的y坐标位置,在这里是在y=0的位置,即x轴位置
# color='k': 线条颜色,'k'表示黑色(black)
# linewidth=0.5: 线条宽度为0.5个像素
# alpha=0.5: 线条透明度,0.5表示半透明
ax1.axhline(y=0, color='k', linewidth=0.5, alpha=0.5)
ax1.axvline(x=0, color='k', linewidth=0.5, alpha=0.5)
# 标题
ax1.set_title('一次函数', fontsize=14, fontweight='bold')
ax1.set_xlabel('x')
ax1.set_ylabel('y')
# 设置x轴的最小值为-10,最大值为10
ax1.set_xlim(-10, 10)
# 设置y轴的最小值为-10,最大值为10
ax1.set_ylim(-10, 10)
# 为图表添加网格线:
ax1.grid(True, alpha=0.3)
# 显示图例,用于标识图表中的不同数据系列 指定图例显示在图表的左上角位置
ax1.legend(loc='upper left')
# 设置坐标轴的纵横比 'equal' 表示x轴和y轴的比例相等,即单位长度相同
# adjustable='box' 表示通过调整坐标轴的边界框来保持比例
ax1.set_aspect('equal', adjustable='box')
python
def plot_quadratic_function(gs):
"""
二次函数 y = x²
:param gs:
:return:
"""
ax = fig.add_subplot(gs[0, 1])
x = np.linspace(-10, 10, 400)
y = x ** 2
ax.plot(x, y, 'r-', linewidth=2, label='y = x²')
ax.axhline(y=0, color='k', linewidth=0.5, alpha=0.5)
ax.axvline(x=0, color='k', linewidth=0.5, alpha=0.5)
ax.set_title('二次函数', fontsize=14, fontweight='bold')
ax.set_xlabel('x')
ax.set_ylabel('y')
# x 轴的最小值为-5,最大值为5
ax.set_xlim(-5, 5)
# y 轴的最小值为-2,最大值为10
ax.set_ylim(-2, 10)
ax.grid(True, alpha=0.3)
ax.legend(loc='upper center')
ax.set_aspect('equal', adjustable='box')
python
def plot_inverse_proportion_function(gs):
"""
正比例函数 y = x
:param gs:
:return:
"""
ax = fig.add_subplot(gs[0, 2])
# 创建从-10到-0.1的200个均匀分布的数据点 避开x=0点,防止除零错误
x_begin=np.linspace(-10, -0.1, 200)
# 创建从0.1到10的200个均匀分布的数据点 同样避开x=0点
x_end=np.linspace(0.1, 10, 200)
# 使用 np.concatenate 将 x_begin 和 x_end 两个数组连接成一个完整的数组
x = np.concatenate([x_begin,x_end ])
y = 1 / x
# g表示green
ax.plot(x, y, 'g-', linewidth=2, label='y = 1/x')
ax.axhline(y=0, color='k', linewidth=0.5, alpha=0.5)
ax.axvline(x=0, color='k', linewidth=0.5, alpha=0.5)
ax.set_title('反比例函数', fontsize=14, fontweight='bold')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_xlim(-10, 10)
ax.set_ylim(-10, 10)
ax.grid(True, alpha=0.3)
ax.legend(loc='upper left')
ax.set_aspect('equal', adjustable='box')
python
def plot_proportion_function(gs):
"""
正比例函数 y = x
:param gs:
:return:
"""
x = np.linspace(-10, 10, 400)
ax = fig.add_subplot(gs[1, 0])
y = x
ax.plot(x, x, 'm-', linewidth=2, label='y = x')
ax.axhline(y=0, color='k', linewidth=0.5, alpha=0.5)
ax.axvline(x=0, color='k', linewidth=0.5, alpha=0.5)
ax.set_title('正比例函数', fontsize=14, fontweight='bold')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_xlim(-10, 10)
ax.set_ylim(-10, 10)
ax.grid(True, alpha=0.3)
ax.legend(loc='upper left')
ax.set_aspect('equal', adjustable='box')
python
def plot_constant_function(gs):
"""
常数函数 y = 3
:param gs:
:return:
"""
ax = fig.add_subplot(gs[1, 1])
x = np.linspace(-10, 10, 400)
# x所有元素都等于1
y = np.ones_like(x) * 3
ax.plot(x, y, 'c-', linewidth=2, label='y = 3')
ax.axhline(y=0, color='k', linewidth=0.5, alpha=0.5)
ax.axvline(x=0, color='k', linewidth=0.5, alpha=0.5)
ax.set_title('常数函数', fontsize=14, fontweight='bold')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_xlim(-10, 10)
ax.set_ylim(-5, 5)
ax.grid(True, alpha=0.3)
ax.legend(loc='upper right')
ax.set_aspect('equal', adjustable='box')
python
def plot_absolute_value_function(gs):
"""
绝对值函数 y = |x|
:param gs:
:return:
"""
ax = fig.add_subplot(gs[1, 2])
x = np.linspace(-10, 10, 400)
y = np.abs(x)
ax.plot(x, y, 'y-', linewidth=2, label='y = |x|')
ax.axhline(y=0, color='k', linewidth=0.5, alpha=0.5)
ax.axvline(x=0, color='k', linewidth=0.5, alpha=0.5)
ax.set_title('绝对值函数', fontsize=14, fontweight='bold')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_xlim(-10, 10)
ax.set_ylim(-2, 10)
ax.grid(True, alpha=0.3)
ax.legend(loc='upper center')
ax.set_aspect('equal', adjustable='box')