《机器学习导论》第 10 章-线性判别式

大家好！今天给大家分享《机器学习导论》第 10 章的核心内容 ------线性判别式 。线性判别式是机器学习中非常经典的分类方法，它不像神经网络那么复杂，但却是理解分类问题的基础。这篇帖子会尽量避开繁杂的公式，用通俗的语言 + 可直接运行的 Python 代码 + 直观的可视化对比，帮大家彻底搞懂线性判别式的核心思想和应用。

所有代码均已在 Mac 系统测试通过，Matplotlib 中文显示配置已适配，直接复制即可运行！

10.1 引言

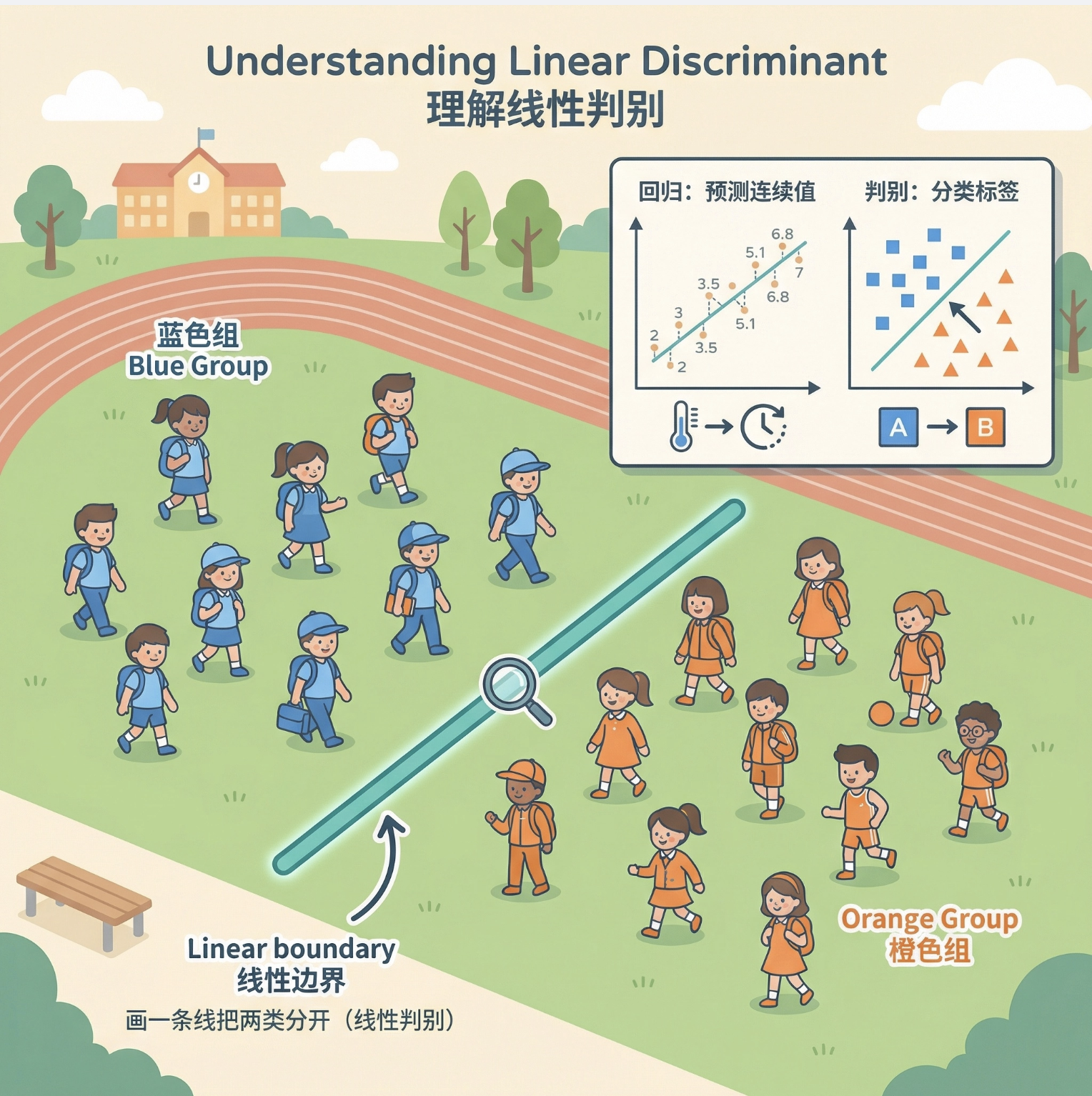
线性判别式（Linear Discriminant, LD）本质上是用直线 / 超平面把不同类别的数据分开的方法。

你可以把它想象成：在操场上有两群不同班级的学生，你需要画一条线，让一班的学生都在线左边，二班的都在线右边 ------ 这条线就是线性判别式。

它和我们之前学的线性回归不同：回归是 "预测一个连续值"（比如预测房价），而判别式是 "判断类别"（比如判断是猫还是狗）。

10.2 推广线性模型

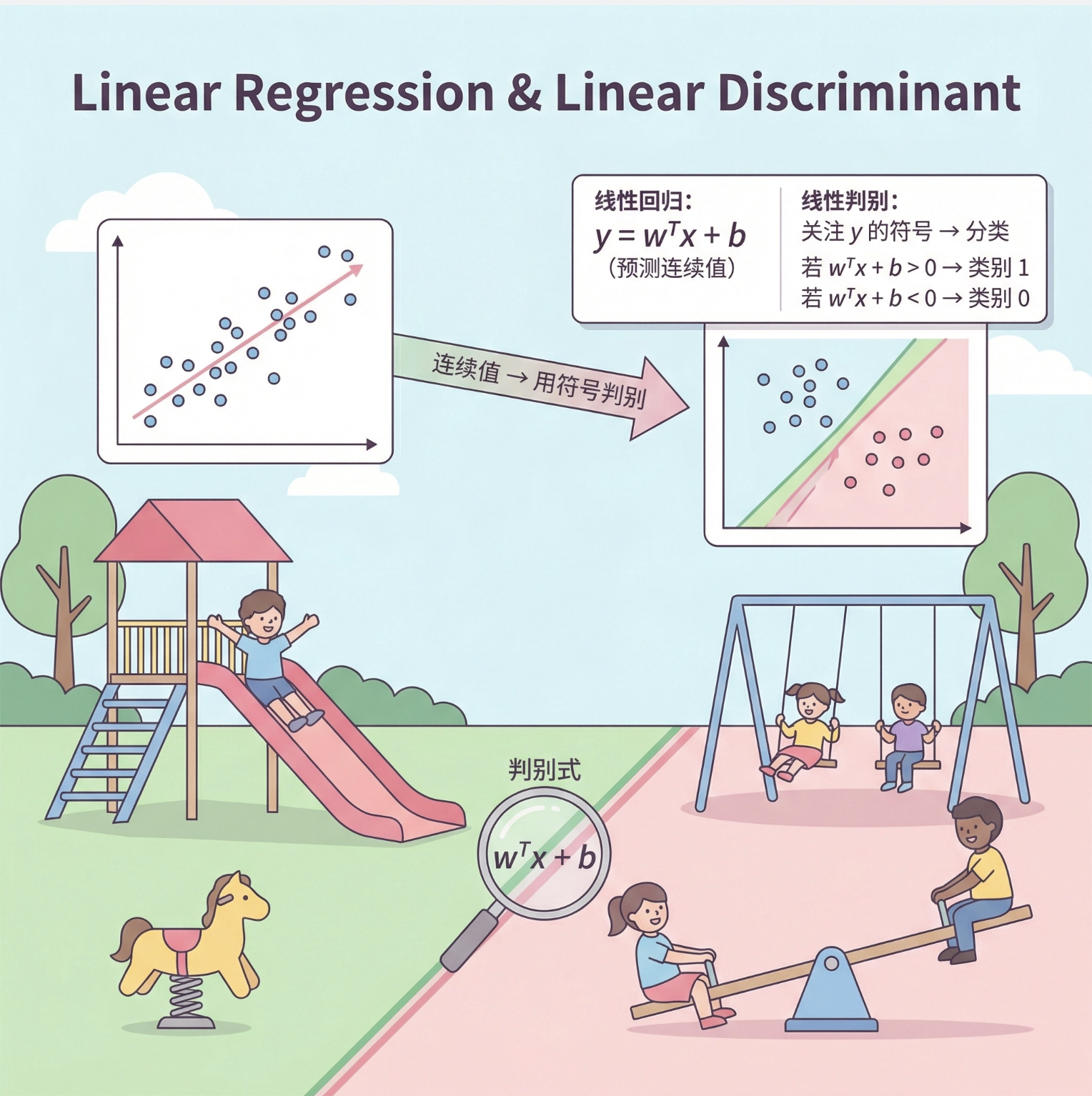
线性回归的公式是 y=wTx+b（预测连续值），而线性判别式是对这个模型的 "分类化改造"：

我们不再关注 y 的具体数值，而是关注 y 的符号 / 大小对应的类别；
比如：当 wTx+b>0 时，判定为类别 1；当 wTx+b<0 时，判定为类别 0。

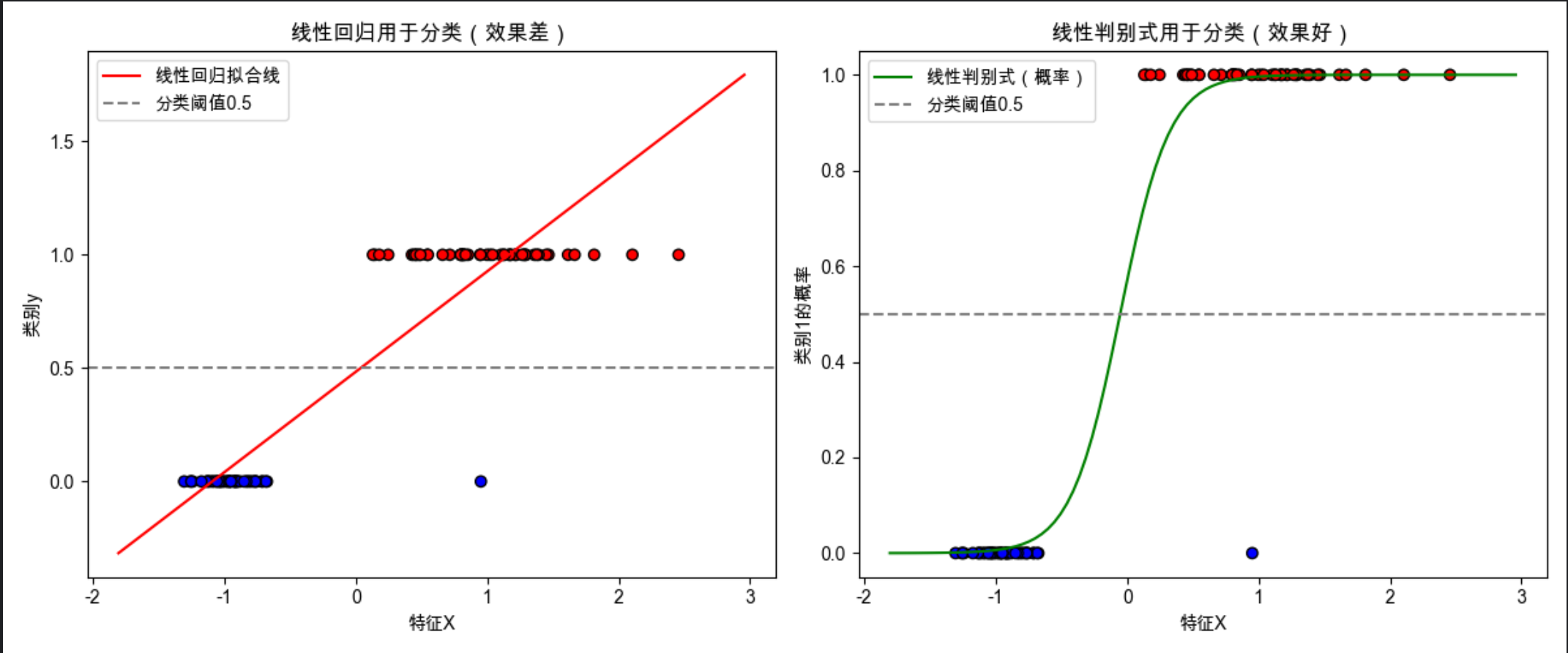
代码：线性回归 vs 线性判别式基础对比

复制代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression, LogisticRegression
from sklearn.datasets import make_classification

# Mac系统Matplotlib中文显示配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'

# 生成模拟分类数据
X, y = make_classification(
    n_samples=100, n_features=1, n_informative=1, 
    n_redundant=0, n_classes=2, n_clusters_per_class=1,
    random_state=42
)

# 1. 线性回归（错误的分类方式）
lr = LinearRegression()
lr.fit(X, y)
x_range = np.linspace(X.min()-0.5, X.max()+0.5, 100).reshape(-1, 1)
y_lr = lr.predict(x_range)

# 2. 线性判别式（逻辑斯蒂回归，本质是线性判别）
ld = LogisticRegression(penalty=None)
ld.fit(X, y)
y_ld = ld.predict_proba(x_range)[:, 1]  # 类别1的概率

# 可视化对比
plt.figure(figsize=(12, 5))

# 子图1：线性回归做分类
plt.subplot(1, 2, 1)
plt.scatter(X, y, c=y, cmap='bwr', edgecolors='k')
plt.plot(x_range, y_lr, 'r-', label='线性回归拟合线')
plt.axhline(y=0.5, color='gray', linestyle='--', label='分类阈值0.5')
plt.title('线性回归用于分类（效果差）')
plt.xlabel('特征X')
plt.ylabel('类别y')
plt.legend()

# 子图2：线性判别式（逻辑斯蒂）做分类
plt.subplot(1, 2, 2)
plt.scatter(X, y, c=y, cmap='bwr', edgecolors='k')
plt.plot(x_range, y_ld, 'g-', label='线性判别式（概率）')
plt.axhline(y=0.5, color='gray', linestyle='--', label='分类阈值0.5')
plt.title('线性判别式用于分类（效果好）')
plt.xlabel('特征X')
plt.ylabel('类别1的概率')
plt.legend()

plt.tight_layout()
plt.show()

代码解释：

make_classification：生成模拟的二分类数据（1 个特征，2 个类别）；
线性回归拟合的是 "连续值"，当用 0.5 作为分类阈值时，会出现明显的分类错误；
线性判别式（逻辑斯蒂回归）输出的是 "类别概率"，能更合理地划分类别边界。

10.3 线性判别式的几何意义

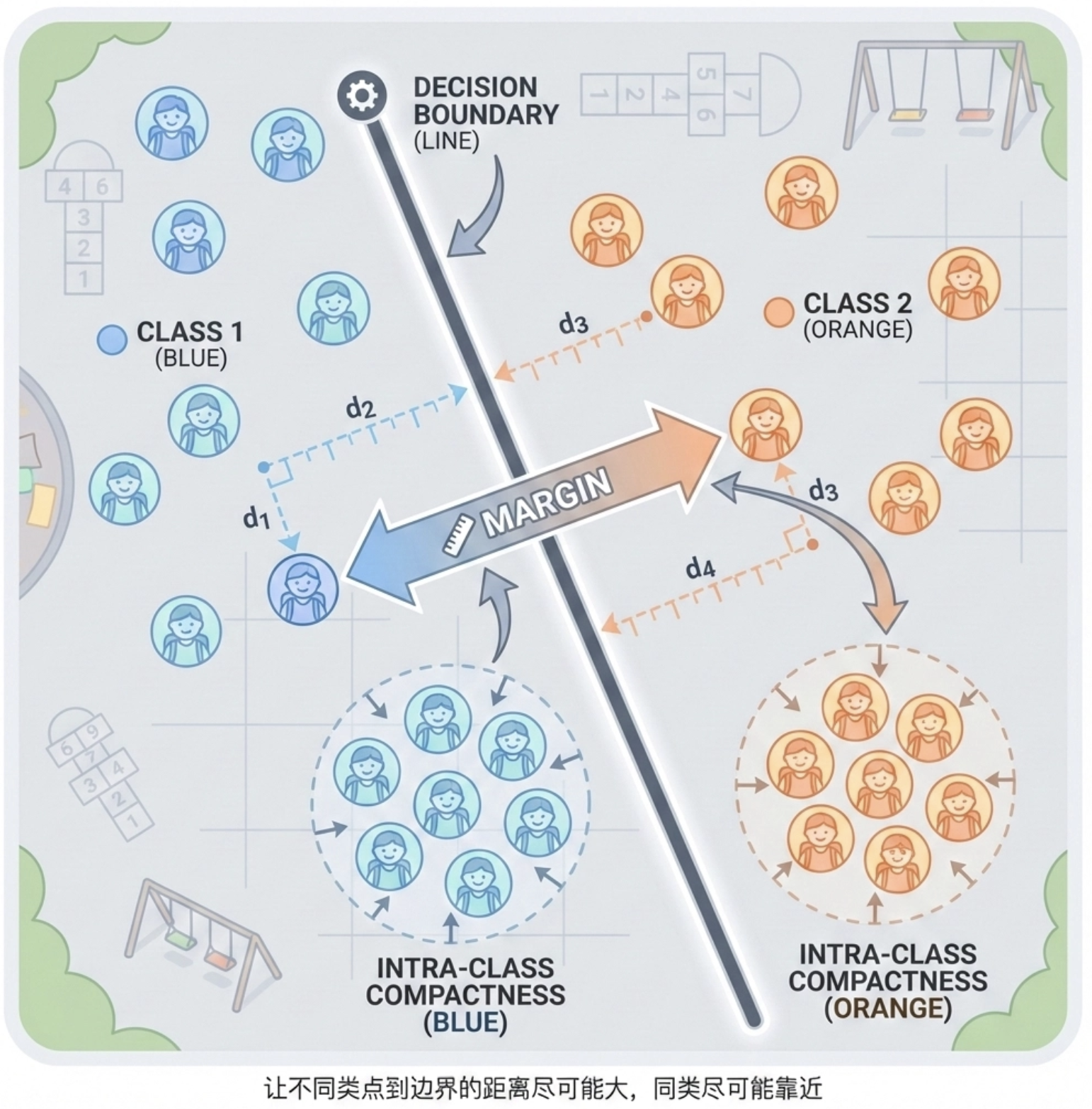
线性判别式的核心是找到一个决策边界 （直线 / 超平面），几何上可以理解为：让不同类别的数据点到这个边界的距离尽可能远，同时同类数据点尽可能靠近。

10.3.1 两类问题

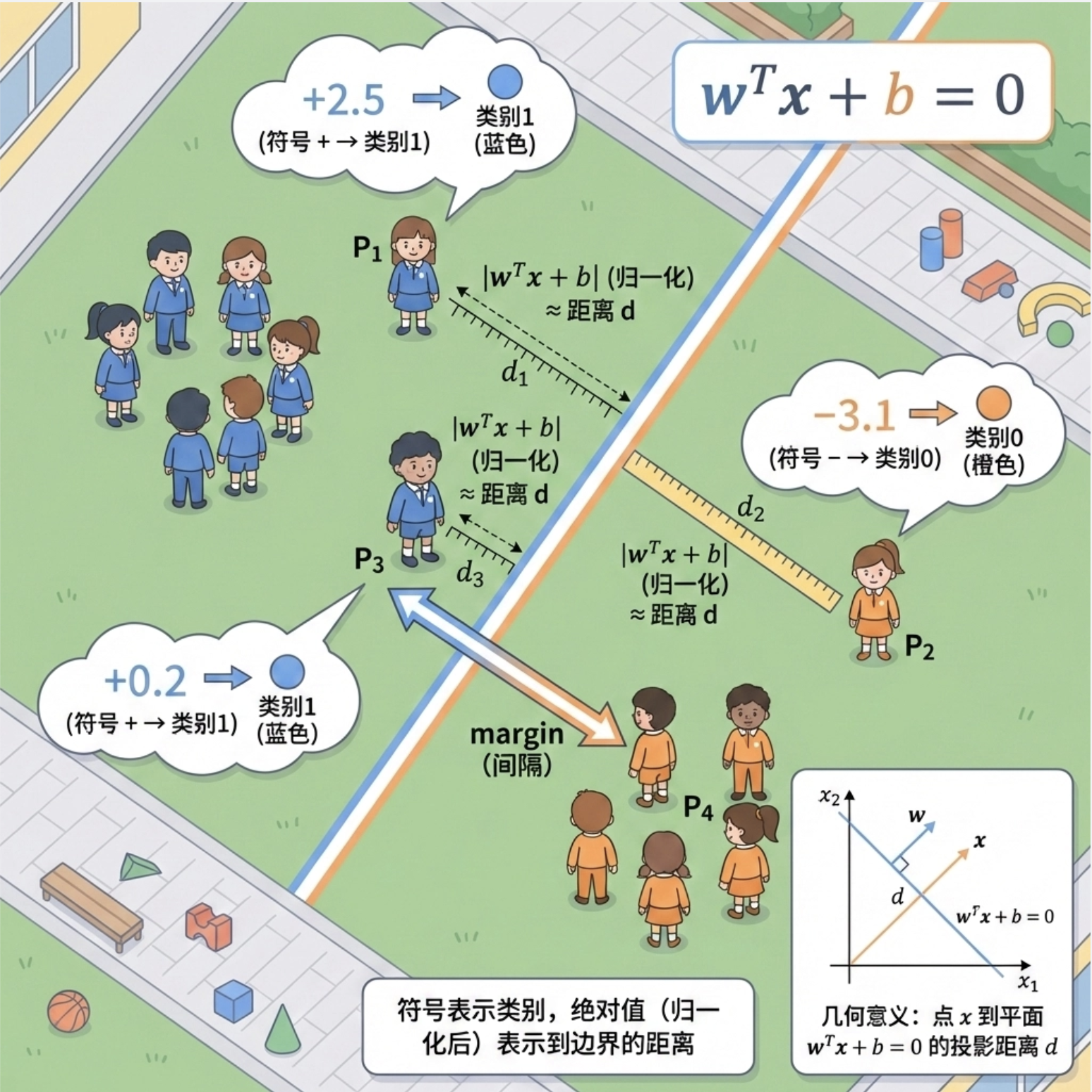
对于两类问题，决策边界是一条直线（2 维）或超平面（高维），公式为：wTx+b=0。

数据点 x 代入公式，结果的符号代表类别；
结果的绝对值代表数据点到决策边界的距离（归一化后）。

10.3.2 多类问题

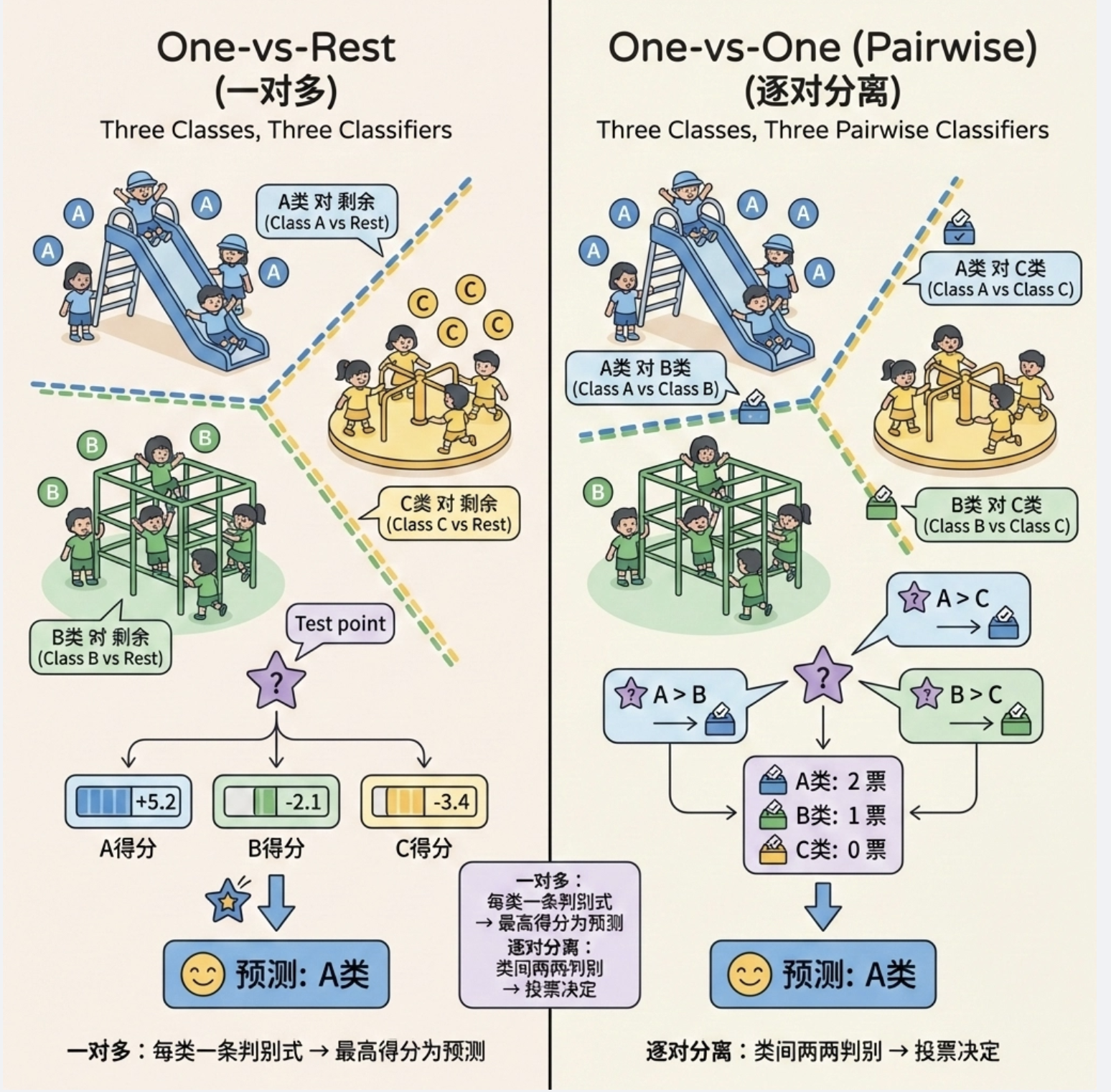
多类问题的线性判别式有两种思路：

一对多（One-vs-Rest）：为每个类别训练一个判别式，判断 "是 / 不是该类别"；
逐对分离（后面 10.4 讲） ：为每两个类别训练一个判别式，最终通过投票确定类别。

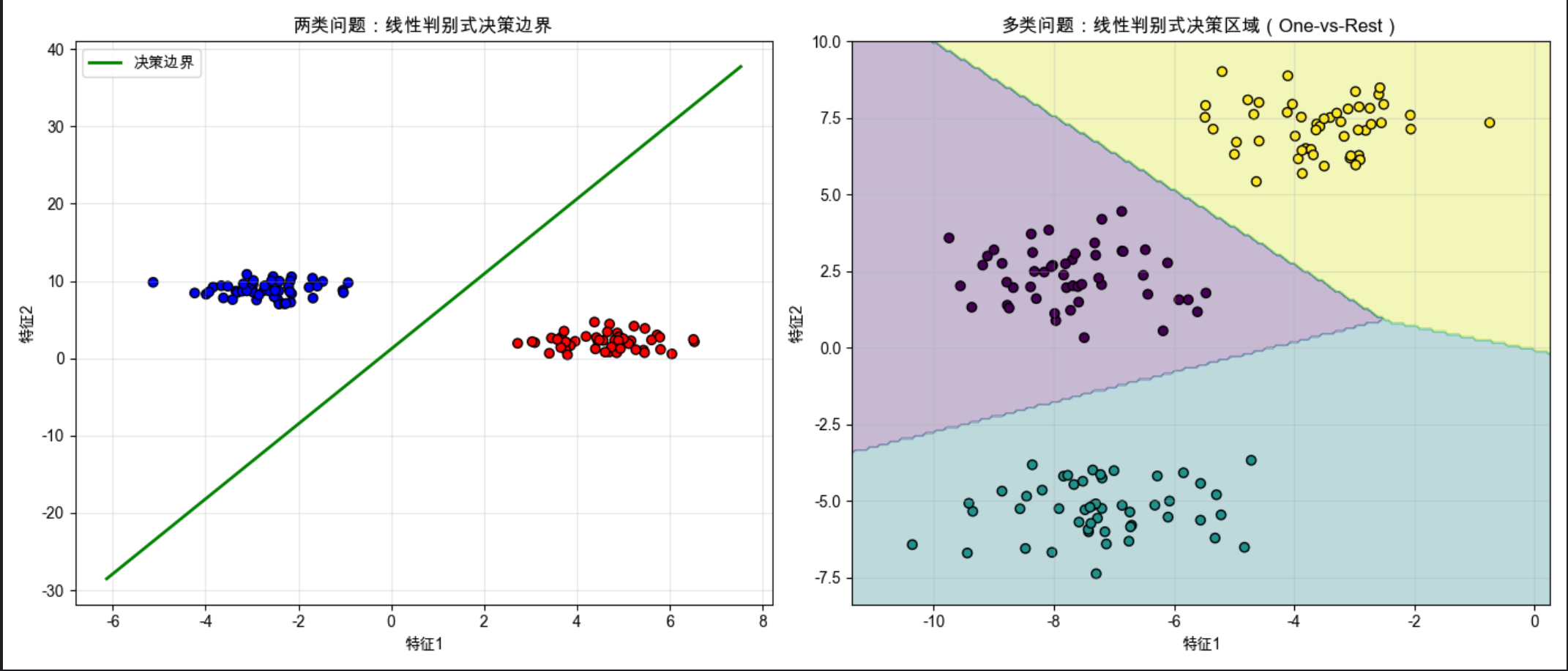
代码：两类 / 多类线性判别式几何可视化

复制代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import make_blobs

# Mac字体配置（同上）
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'

# ========== 1. 两类问题可视化 ==========
# 生成两类数据（2维）
X_2class, y_2class = make_blobs(
    n_samples=100, n_features=2, centers=2, cluster_std=1.0,
    random_state=42
)
# 训练线性判别式
clf_2class = LogisticRegression(penalty=None, random_state=42)
clf_2class.fit(X_2class, y_2class)

# 提取决策边界参数 w1*x1 + w2*x2 + b = 0 → x2 = (-w1*x1 -b)/w2
w = clf_2class.coef_[0]
b = clf_2class.intercept_[0]
x1_range = np.linspace(X_2class[:,0].min()-1, X_2class[:,0].max()+1, 100)
x2_boundary = (-w[0]*x1_range - b) / w[1]

# ========== 2. 多类问题可视化 ==========
# 生成三类数据（2维）
X_3class, y_3class = make_blobs(
    n_samples=150, n_features=2, centers=3, cluster_std=1.0,
    random_state=43
)
# 训练多类线性判别式（默认One-vs-Rest）
clf_3class = LogisticRegression(penalty=None, random_state=42, multi_class='ovr')
clf_3class.fit(X_3class, y_3class)

# 生成网格用于绘制决策区域
x1_min, x1_max = X_3class[:,0].min()-1, X_3class[:,0].max()+1
x2_min, x2_max = X_3class[:,1].min()-1, X_3class[:,1].max()+1
xx, yy = np.meshgrid(np.linspace(x1_min, x1_max, 200),
                     np.linspace(x2_min, x2_max, 200))
Z = clf_3class.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

# ========== 绘制对比图 ==========
plt.figure(figsize=(14, 6))

# 子图1：两类问题决策边界
plt.subplot(1, 2, 1)
plt.scatter(X_2class[:,0], X_2class[:,1], c=y_2class, cmap='bwr', edgecolors='k')
plt.plot(x1_range, x2_boundary, 'g-', linewidth=2, label='决策边界')
plt.title('两类问题：线性判别式决策边界')
plt.xlabel('特征1')
plt.ylabel('特征2')
plt.legend()
plt.grid(alpha=0.3)

# 子图2：多类问题决策区域
plt.subplot(1, 2, 2)
plt.contourf(xx, yy, Z, alpha=0.3, cmap='viridis')
plt.scatter(X_3class[:,0], X_3class[:,1], c=y_3class, cmap='viridis', edgecolors='k')
plt.title('多类问题：线性判别式决策区域（One-vs-Rest）')
plt.xlabel('特征1')
plt.ylabel('特征2')
plt.grid(alpha=0.3)

plt.tight_layout()
plt.show()

代码解释：

两类问题：直接画出决策边界直线，直观看到 "一条线分开两类数据"；
多类问题：用contourf绘制决策区域，每个区域对应一个类别，能清晰看到多个线性边界划分的结果。

10.4 逐对分离

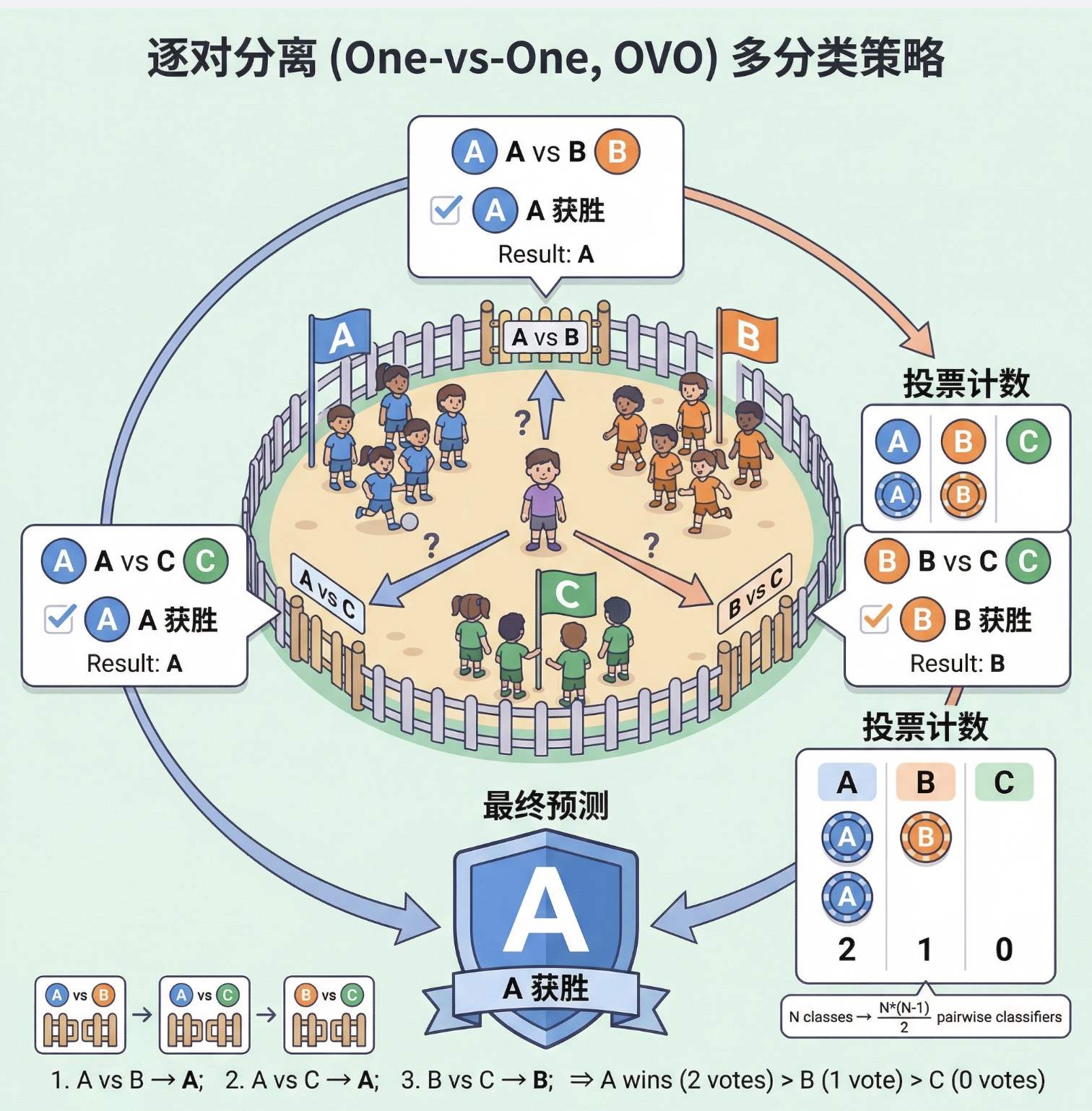
逐对分离（One-vs-One, OVO）是多类分类的另一种策略，思路很简单：

有 N 个类别，就为每两个类别训练一个线性判别式（共 N*(N-1)/2 个），最终对一个新样本，让所有判别式 "投票"，得票最多的类别就是预测结果。

比如 3 个类别（A、B、C）：

训练 A vs B、A vs C、B vs C 三个判别式；
新样本输入后，A vs B 判为 A，A vs C 判为 A，B vs C 判为 B → A 得 2 票，最终预测为 A。

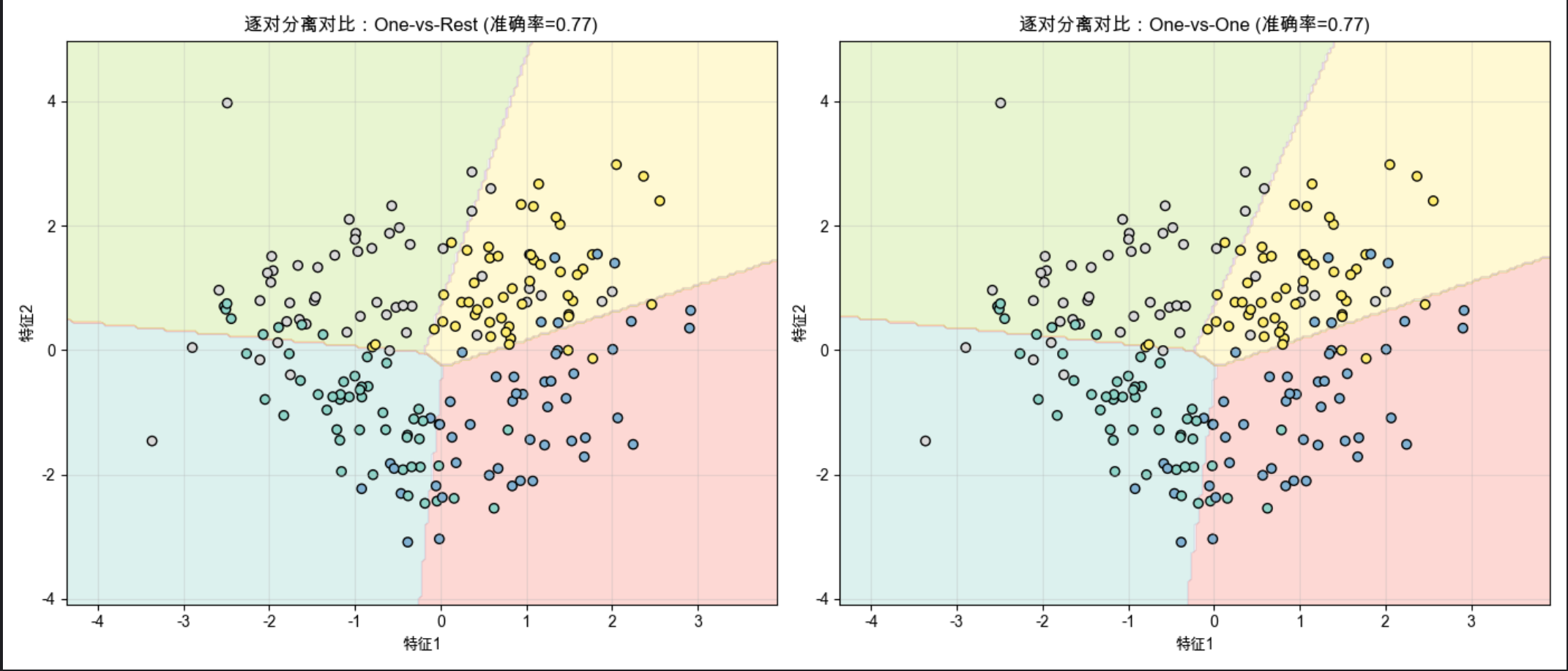
代码：One-vs-Rest vs One-vs-One 效果对比

复制代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import make_classification
from sklearn.metrics import accuracy_score

# Mac字体配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'

# 生成4类高重叠数据（增加分类难度）
X, y = make_classification(
    n_samples=200, n_features=2, n_informative=2, n_redundant=0,
    n_classes=4, n_clusters_per_class=1, class_sep=1.0, random_state=42
)

# 1. One-vs-Rest (OvR)
ovr_clf = LogisticRegression(penalty=None, multi_class='ovr', random_state=42)
ovr_clf.fit(X, y)
ovr_pred = ovr_clf.predict(X)
ovr_acc = accuracy_score(y, ovr_pred)

# 2. One-vs-One (OvO)
ovo_clf = LogisticRegression(penalty=None, multi_class='multinomial', solver='lbfgs', random_state=42)
ovo_clf.fit(X, y)
ovo_pred = ovo_clf.predict(X)
ovo_acc = accuracy_score(y, ovo_pred)

# 生成网格绘制决策区域
x1_min, x1_max = X[:,0].min()-1, X[:,0].max()+1
x2_min, x2_max = X[:,1].min()-1, X[:,1].max()+1
xx, yy = np.meshgrid(np.linspace(x1_min, x1_max, 200),
                     np.linspace(x2_min, x2_max, 200))

# 预测网格点类别
Z_ovr = ovr_clf.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)
Z_ovo = ovo_clf.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)

# 绘制对比图
plt.figure(figsize=(14, 6))

# 子图1：OvR
plt.subplot(1, 2, 1)
plt.contourf(xx, yy, Z_ovr, alpha=0.3, cmap='Set3')
plt.scatter(X[:,0], X[:,1], c=y, cmap='Set3', edgecolors='k')
plt.title(f'逐对分离对比：One-vs-Rest (准确率={ovr_acc:.2f})')
plt.xlabel('特征1')
plt.ylabel('特征2')
plt.grid(alpha=0.3)

# 子图2：OvO
plt.subplot(1, 2, 2)
plt.contourf(xx, yy, Z_ovo, alpha=0.3, cmap='Set3')
plt.scatter(X[:,0], X[:,1], c=y, cmap='Set3', edgecolors='k')
plt.title(f'逐对分离对比：One-vs-One (准确率={ovo_acc:.2f})')
plt.xlabel('特征1')
plt.ylabel('特征2')
plt.grid(alpha=0.3)

plt.tight_layout()
plt.show()

代码解释：

multi_class='ovr'：启用一对多策略；
multi_class='multinomial'+solver='lbfgs'：启用逐对分离策略；
在数据有重叠时，OvO 通常比 OvR 准确率更高（但训练时间更长）。

10.5 参数判别式的进一步讨论

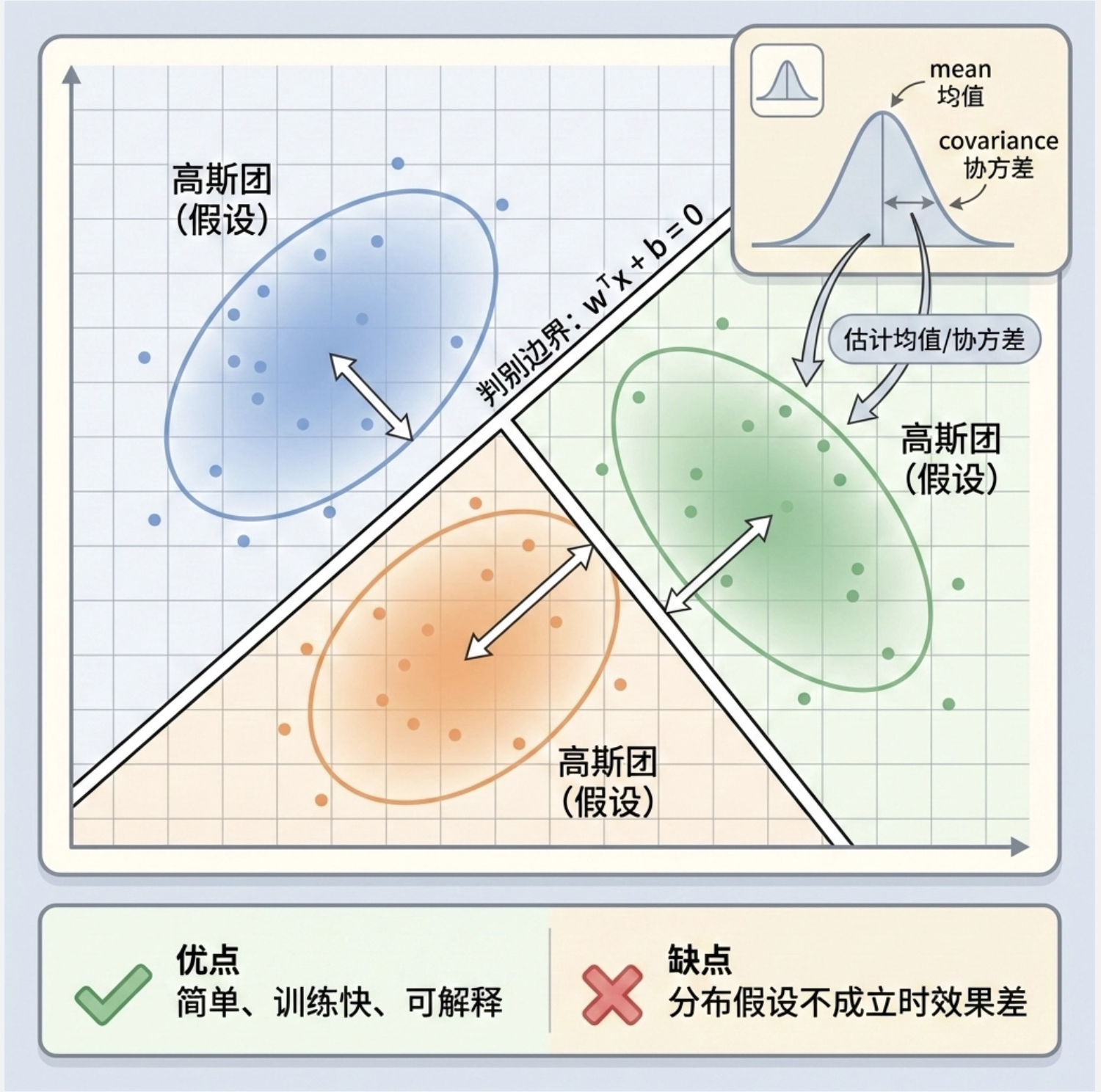
参数判别式（比如线性判别式）的核心是假设数据服从某种分布（比如高斯分布） ，然后通过估计分布的参数（均值、方差）来确定决策边界。

你可以把它理解为：

先假设每个类别的数据都是 "圆形 / 椭圆形的团"（高斯分布），然后找到能最优分割这些 "团" 的直线。

参数判别式的优缺点：

✅ 优点：模型简单、训练快、可解释性强；
❌ 缺点：如果数据分布不符合假设（比如非高斯），效果会很差。

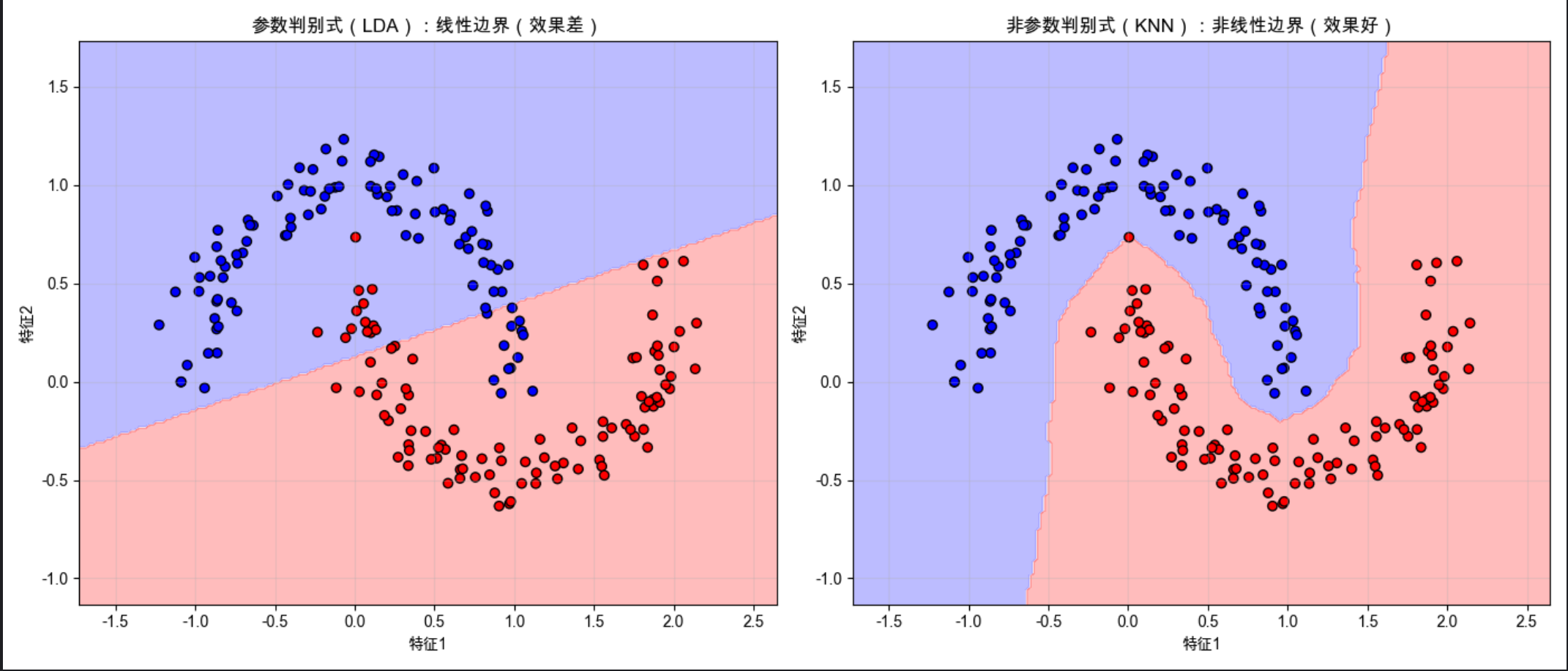
代码：参数判别式（LDA）vs 非参数判别式（KNN）对比

复制代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import make_moons

# Mac字体配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'

# 生成非高斯分布数据（月亮形，线性不可分）
X, y = make_moons(n_samples=200, noise=0.1, random_state=42)

# 1. 参数判别式：线性判别分析（LDA）
lda = LinearDiscriminantAnalysis()
lda.fit(X, y)

# 2. 非参数判别式：K近邻（KNN）
knn = KNeighborsClassifier(n_neighbors=5)
knn.fit(X, y)

# 生成网格
x1_min, x1_max = X[:,0].min()-0.5, X[:,0].max()+0.5
x2_min, x2_max = X[:,1].min()-0.5, X[:,1].max()+0.5
xx, yy = np.meshgrid(np.linspace(x1_min, x1_max, 200),
                     np.linspace(x2_min, x2_max, 200))

# 预测网格类别
Z_lda = lda.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)
Z_knn = knn.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)

# 绘制对比图
plt.figure(figsize=(14, 6))

# 子图1：LDA（参数判别式）
plt.subplot(1, 2, 1)
plt.contourf(xx, yy, Z_lda, alpha=0.3, cmap='bwr')
plt.scatter(X[:,0], X[:,1], c=y, cmap='bwr', edgecolors='k')
plt.title('参数判别式（LDA）：线性边界（效果差）')
plt.xlabel('特征1')
plt.ylabel('特征2')
plt.grid(alpha=0.3)

# 子图2：KNN（非参数判别式）
plt.subplot(1, 2, 2)
plt.contourf(xx, yy, Z_knn, alpha=0.3, cmap='bwr')
plt.scatter(X[:,0], X[:,1], c=y, cmap='bwr', edgecolors='k')
plt.title('非参数判别式（KNN）：非线性边界（效果好）')
plt.xlabel('特征1')
plt.ylabel('特征2')
plt.grid(alpha=0.3)

plt.tight_layout()
plt.show()

代码解释：

月亮形数据是线性不可分的，参数判别式（LDA）只能用直线分割，效果差；
非参数判别式（KNN）不需要假设数据分布，能拟合非线性边界，效果更好。

10.6 梯度下降

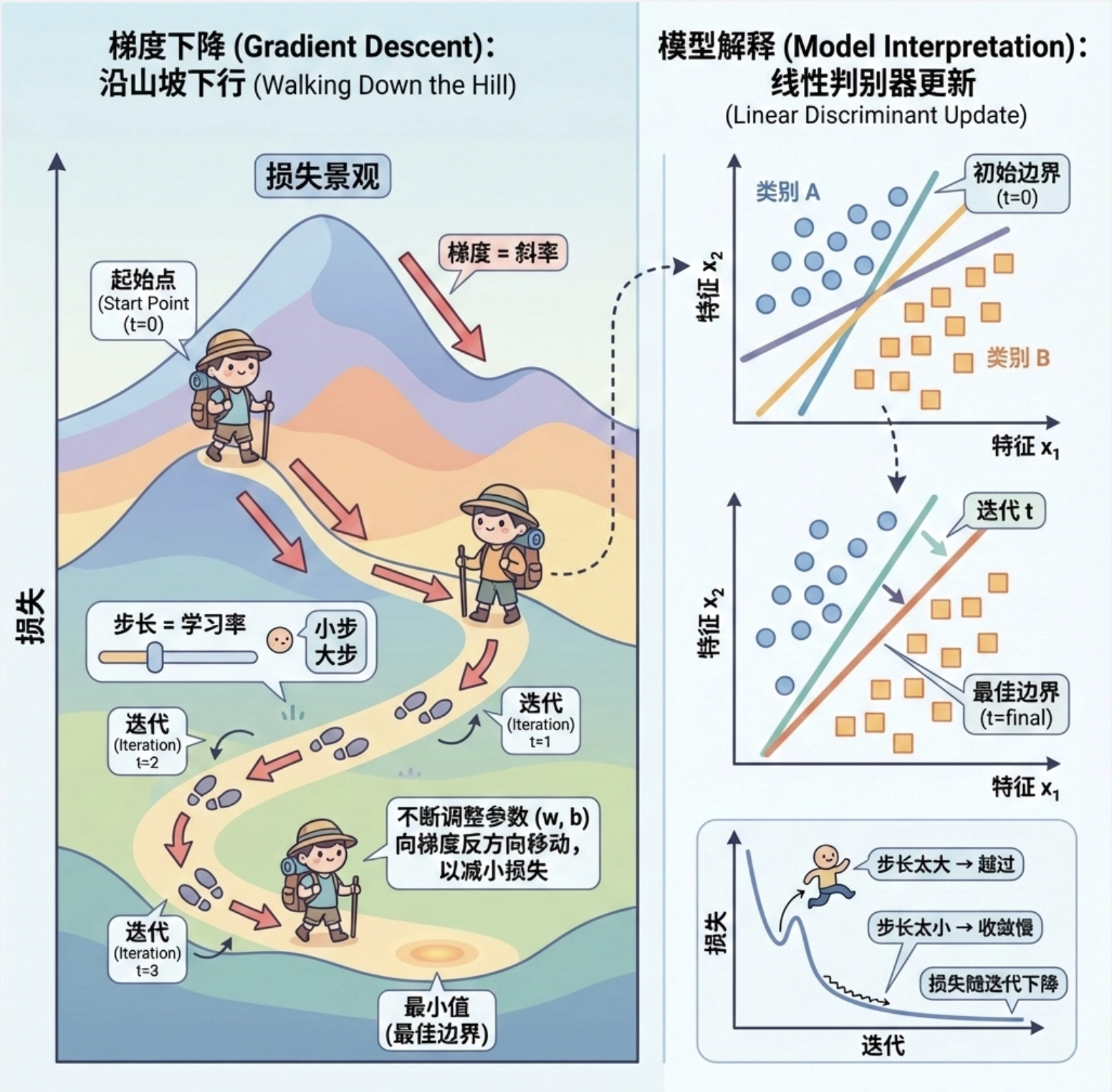
梯度下降是训练线性判别式的核心优化算法，思路就像 "下山"：

我们的目标是找到最优的决策边界（山顶的最低点），梯度就是 "坡度"，每次沿着坡度最陡的方向走一小步，直到走到山脚（损失最小）。

代码：手动实现梯度下降训练线性判别式

复制代码

import numpy as np
import matplotlib.pyplot as plt

# Mac字体配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'

# ========== 1. 定义核心函数 ==========
# sigmoid函数：把线性输出转换为0-1概率（用于二分类）
def sigmoid(z):
    return 1 / (1 + np.exp(-z))

# 损失函数（交叉熵损失）
def loss(y_true, y_pred):
    # 防止log(0)，加微小值
    y_pred = np.clip(y_pred, 1e-10, 1-1e-10)
    return -np.mean(y_true * np.log(y_pred) + (1 - y_true) * np.log(1 - y_pred))

# 梯度下降更新参数
def gradient_descent(X, y, w, b, lr):
    n = len(X)
    z = np.dot(X, w) + b
    y_pred = sigmoid(z)
    # 计算梯度
    dw = (1/n) * np.dot(X.T, (y_pred - y))
    db = (1/n) * np.sum(y_pred - y)
    # 更新参数
    w -= lr * dw
    b -= lr * db
    return w, b, loss(y, y_pred)

# ========== 2. 生成数据 ==========
X, y = np.random.randn(200, 2), np.random.randint(0, 2, 200)
# 手动构造可分数据（让y=1的样本特征和更大）
X[y==1] = X[y==1] + 1.5

# ========== 3. 初始化参数 ==========
w = np.zeros(X.shape[1])  # 权重
b = 0                     # 偏置
lr = 0.1                  # 学习率
epochs = 1000             # 迭代次数
loss_history = []         # 记录损失变化

# ========== 4. 训练 ==========
for _ in range(epochs):
    w, b, l = gradient_descent(X, y, w, b, lr)
    loss_history.append(l)

# ========== 5. 可视化 ==========
plt.figure(figsize=(12, 5))

# 子图1：损失曲线
plt.subplot(1, 2, 1)
plt.plot(loss_history)
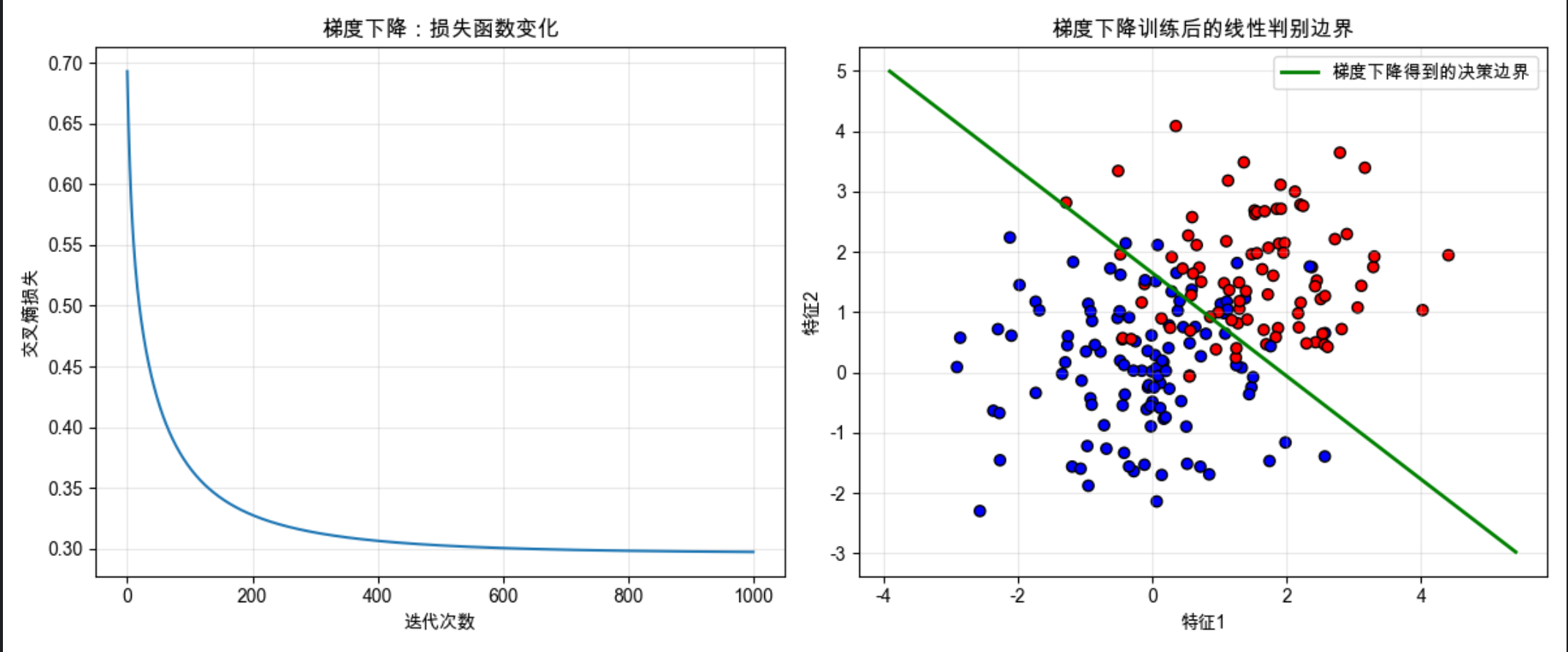
plt.title('梯度下降：损失函数变化')
plt.xlabel('迭代次数')
plt.ylabel('交叉熵损失')
plt.grid(alpha=0.3)

# 子图2：训练后的决策边界
plt.subplot(1, 2, 2)
# 绘制数据点
plt.scatter(X[:,0], X[:,1], c=y, cmap='bwr', edgecolors='k')
# 绘制决策边界（w1*x1 + w2*x2 + b = 0 → x2 = (-w1*x1 -b)/w2）
x1_range = np.linspace(X[:,0].min()-1, X[:,0].max()+1, 100)
x2_boundary = (-w[0]*x1_range - b) / w[1]
plt.plot(x1_range, x2_boundary, 'g-', linewidth=2, label='梯度下降得到的决策边界')
plt.title('梯度下降训练后的线性判别边界')
plt.xlabel('特征1')
plt.ylabel('特征2')
plt.legend()
plt.grid(alpha=0.3)

plt.tight_layout()
plt.show()

代码解释：

sigmoid：把线性输出压缩到 0-1 之间，代表类别 1 的概率；
loss：交叉熵损失，衡量预测值和真实值的差距；
gradient_descent：核心函数，计算梯度并更新权重 / 偏置；
损失曲线会逐渐下降，最终收敛到最小值，说明模型训练有效。

10.7 逻辑斯谛判别式

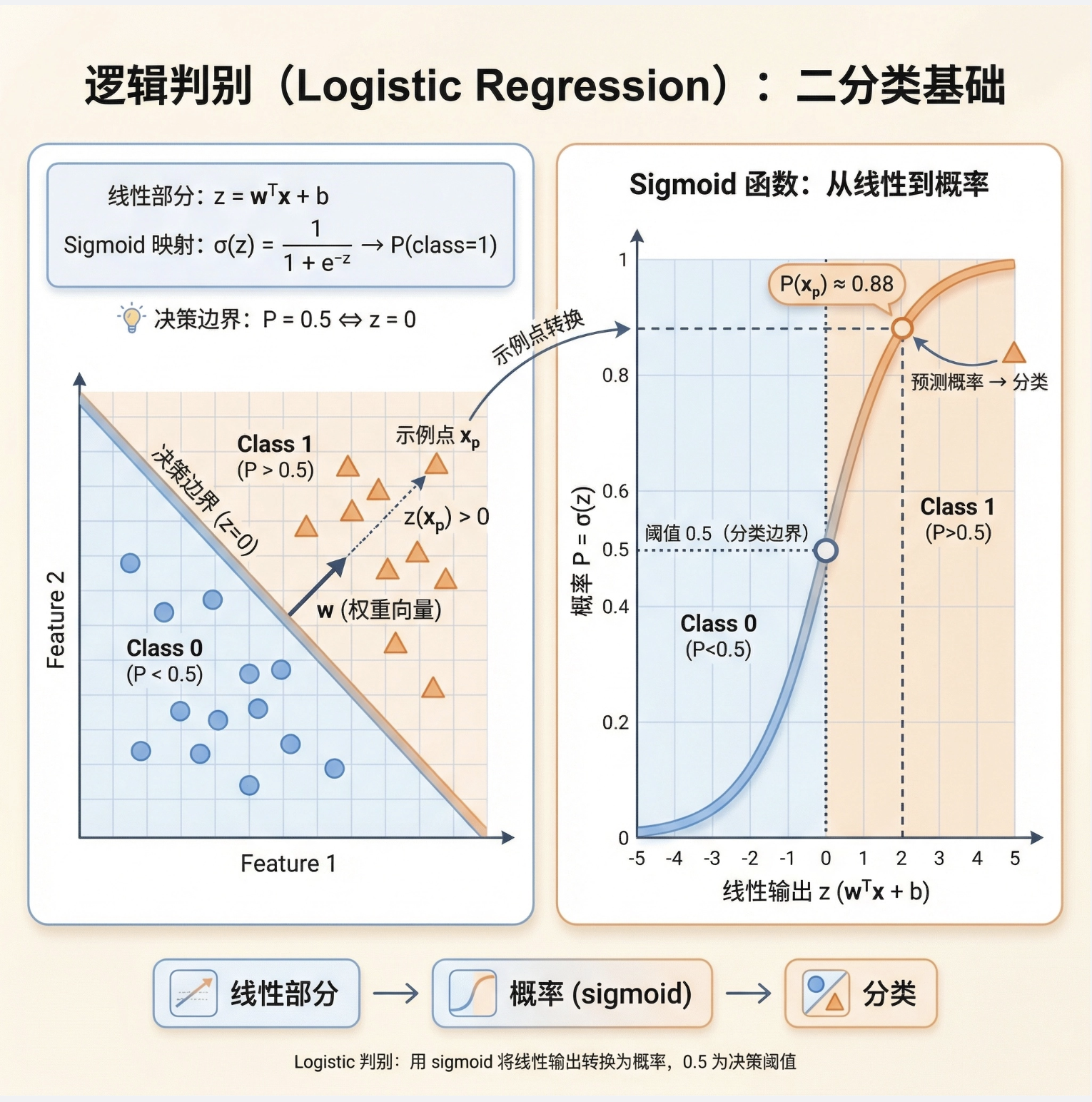
逻辑斯谛判别式（Logistic Discriminant）是最常用的线性判别式，也叫逻辑回归（虽然名字带 "回归"，但实际是分类算法）。

10.7.1 两类问题

两类逻辑斯谛判别式的核心是：

用 sigmoid 函数将线性输出转换为类别概率，决策边界是概率 = 0.5 的位置。

公式：

线性部分：z=wTx+b
概率输出：类别

10.7.2 多类问题

多类逻辑斯谛判别式用Softmax 函数替代 sigmoid，把多个线性输出转换为 "和为 1" 的类别概率，比如 3 类问题：

类别

代码：两类 / 多类逻辑斯谛判别式实战

复制代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import make_blobs
from sklearn.metrics import classification_report

# Mac字体配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'

# ========== 1. 两类逻辑斯谛判别式 ==========
# 生成数据
X_2, y_2 = make_blobs(n_samples=100, n_features=2, centers=2, random_state=42)
# 训练模型
clf_2 = LogisticRegression(penalty=None, random_state=42)
clf_2.fit(X_2, y_2)
# 预测
y_2_pred = clf_2.predict(X_2)
y_2_prob = clf_2.predict_proba(X_2)

# ========== 2. 多类逻辑斯谛判别式 ==========
# 生成数据
X_3, y_3 = make_blobs(n_samples=150, n_features=2, centers=3, random_state=43)
# 训练模型（Softmax）
clf_3 = LogisticRegression(penalty=None, multi_class='multinomial', solver='lbfgs', random_state=42)
clf_3.fit(X_3, y_3)
# 预测
y_3_pred = clf_3.predict(X_3)
y_3_prob = clf_3.predict_proba(X_3)

# ========== 可视化 ==========
plt.figure(figsize=(14, 6))

# 子图1：两类问题（带概率）
plt.subplot(1, 2, 1)
# 绘制数据点（颜色=真实类别，大小=类别1概率）
scatter = plt.scatter(X_2[:,0], X_2[:,1], c=y_2, s=y_2_prob[:,1]*100, 
                      cmap='bwr', edgecolors='k', alpha=0.7)
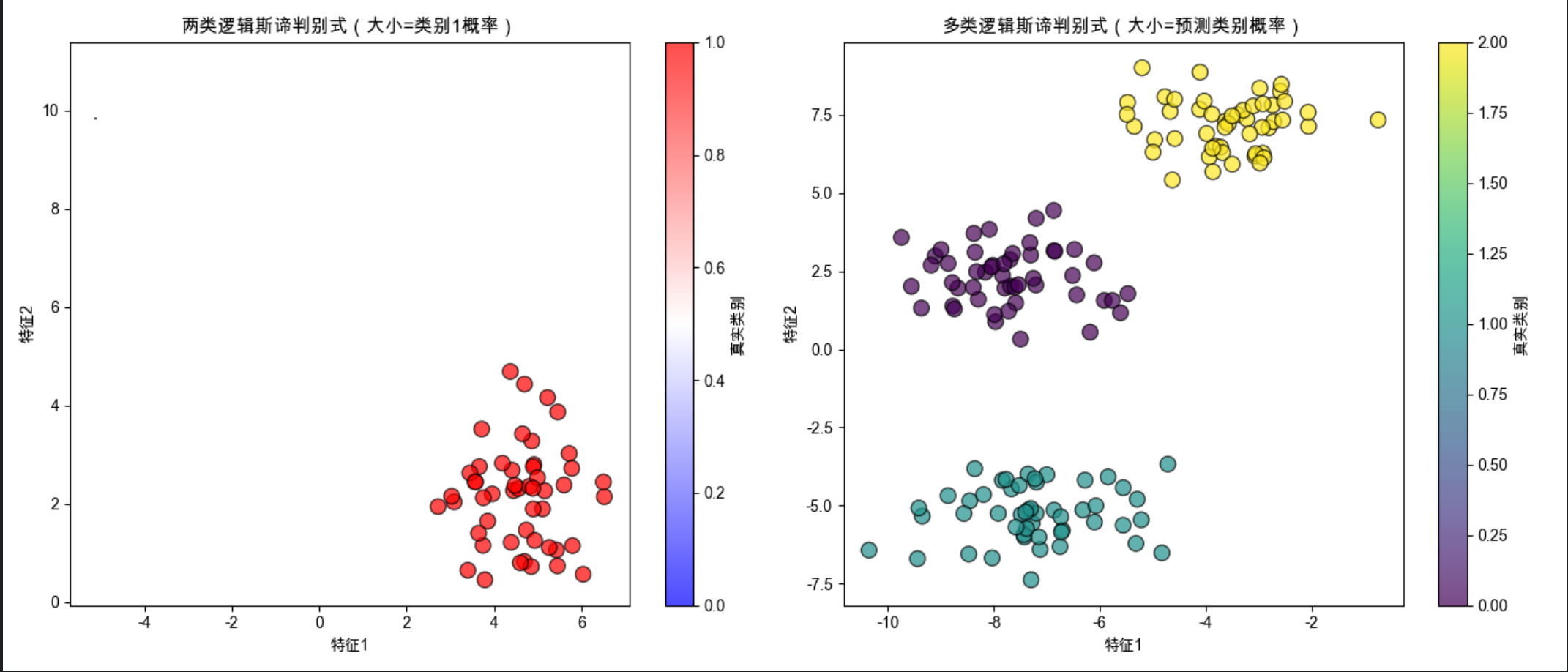
plt.title('两类逻辑斯谛判别式（大小=类别1概率）')
plt.xlabel('特征1')
plt.ylabel('特征2')
plt.colorbar(scatter, label='真实类别')

# 子图2：多类问题（带概率）
plt.subplot(1, 2, 2)
# 绘制数据点（颜色=真实类别，大小=预测类别概率）
max_prob = np.max(y_3_prob, axis=1)
scatter = plt.scatter(X_3[:,0], X_3[:,1], c=y_3, s=max_prob*100, 
                      cmap='viridis', edgecolors='k', alpha=0.7)
plt.title('多类逻辑斯谛判别式（大小=预测类别概率）')
plt.xlabel('特征1')
plt.ylabel('特征2')
plt.colorbar(scatter, label='真实类别')

plt.tight_layout()
plt.show()

# 输出分类报告
print("=== 两类逻辑斯谛判别式分类报告 ===")
print(classification_report(y_2, y_2_pred))
print("\n=== 多类逻辑斯谛判别式分类报告 ===")
print(classification_report(y_3, y_3_pred))

代码解释：

两类问题：用sigmoid输出概率，点的大小代表类别 1 的概率；
多类问题：用Softmax输出概率，点的大小代表预测类别的概率；
classification_report：输出精确率、召回率等指标，评估模型效果。

10.8 回归判别式

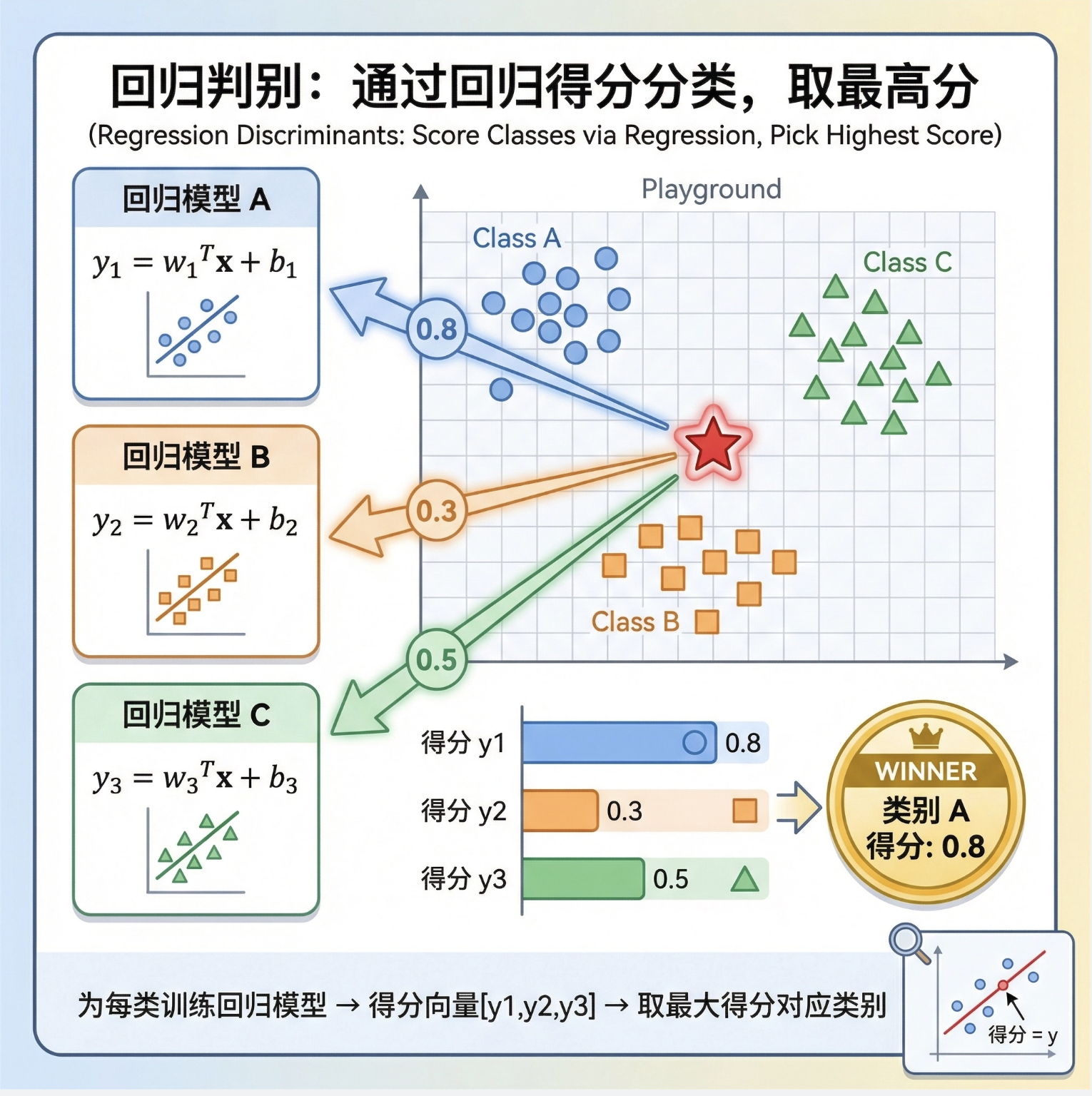
回归判别式是 "用回归的思路做分类"，核心是：

为每个类别训练一个回归模型，预测新样本属于该类别的 "得分"，最终选择得分最高的类别。

比如 3 类问题：训练 3 个回归模型（y1=w1Tx+b1、y2=w2Tx+b2、y3=w3Tx+b3），新样本的得分是[y1,y2,y3]，选最大的那个作为类别。

代码：回归判别式 vs 逻辑斯谛判别式对比

复制代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression, LogisticRegression
from sklearn.datasets import make_classification
from sklearn.metrics import accuracy_score

# Mac字体配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'

# 生成3类分类数据
X, y = make_classification(
    n_samples=200, n_features=2, n_informative=2, n_redundant=0,
    n_classes=3, n_clusters_per_class=1, random_state=42
)

# ========== 1. 回归判别式 ==========
# 为每个类别训练一个回归模型
regressors = []
for cls in range(3):
    # 构造伪标签：当前类别为1，其他为0
    y_cls = np.where(y == cls, 1, 0)
    lr = LinearRegression()
    lr.fit(X, y_cls)
    regressors.append(lr)

# 预测：每个样本在每个类别上的得分 → 选最高得分的类别
reg_scores = np.array([lr.predict(X) for lr in regressors]).T
reg_pred = np.argmax(reg_scores, axis=1)
reg_acc = accuracy_score(y, reg_pred)

# ========== 2. 逻辑斯谛判别式 ==========
log_clf = LogisticRegression(penalty=None, multi_class='multinomial', solver='lbfgs', random_state=42)
log_clf.fit(X, y)
log_pred = log_clf.predict(X)
log_acc = accuracy_score(y, log_pred)

# ========== 可视化 ==========
plt.figure(figsize=(14, 6))

# 子图1：回归判别式
plt.subplot(1, 2, 1)
plt.scatter(X[:,0], X[:,1], c=reg_pred, cmap='viridis', edgecolors='k', alpha=0.7)
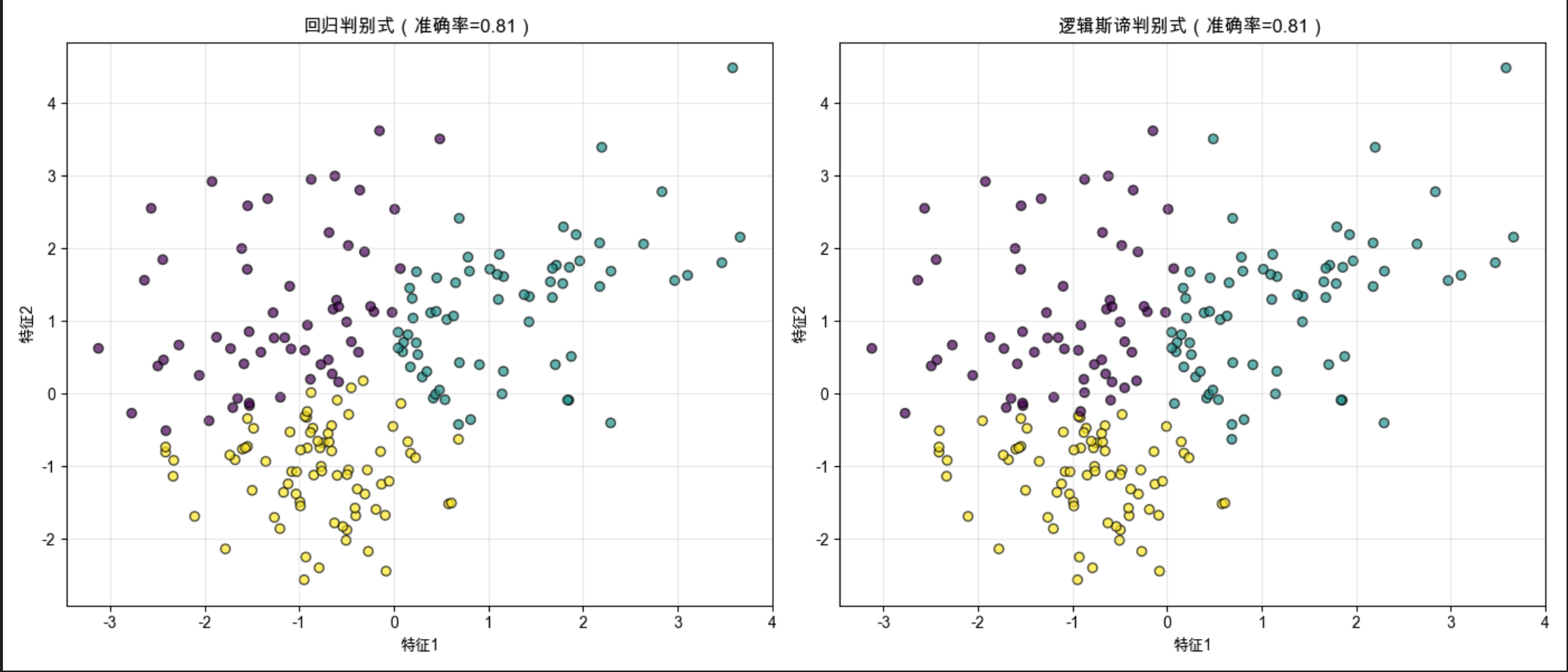
plt.title(f'回归判别式（准确率={reg_acc:.2f}）')
plt.xlabel('特征1')
plt.ylabel('特征2')
plt.grid(alpha=0.3)

# 子图2：逻辑斯谛判别式
plt.subplot(1, 2, 2)
plt.scatter(X[:,0], X[:,1], c=log_pred, cmap='viridis', edgecolors='k', alpha=0.7)
plt.title(f'逻辑斯谛判别式（准确率={log_acc:.2f}）')
plt.xlabel('特征1')
plt.ylabel('特征2')
plt.grid(alpha=0.3)

plt.tight_layout()
plt.show()

代码解释：

回归判别式：为每个类别构建 "伪标签"（1/0），训练回归模型预测得分；
逻辑斯谛判别式：直接优化分类损失，通常比回归判别式准确率更高；
回归判别式的优点是简单易理解，但缺点是对异常值敏感，分类效果不如专门的判别式算法。

10.9 学习排名

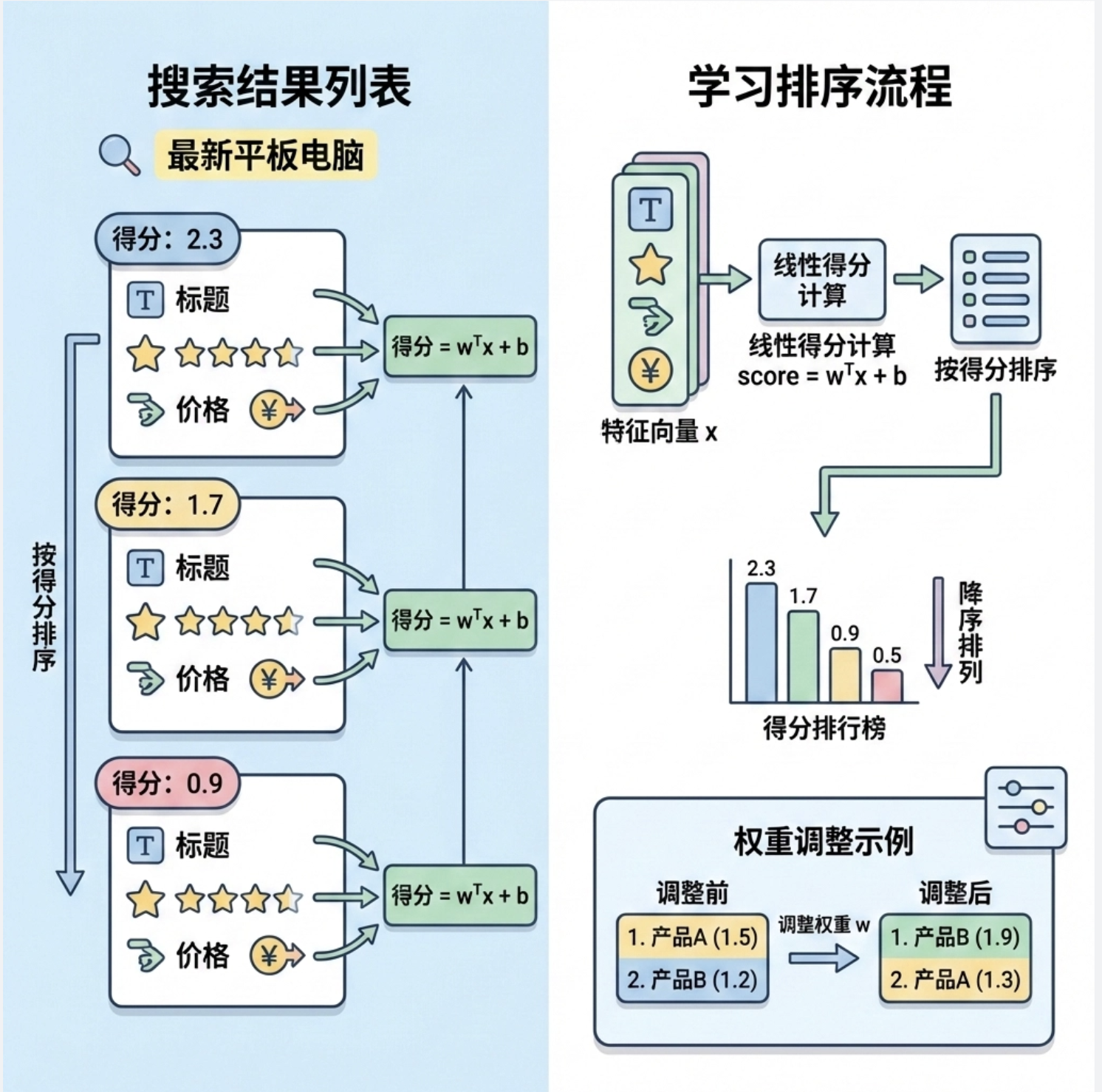
学习排名（Learning to Rank）是线性判别式的一个重要应用，核心是：

给多个样本打分，然后按分数排序，而不是简单的分类。

比如搜索引擎的排序、推荐系统的商品排序，都可以用线性判别式的思路：为每个样本计算一个 "相关性得分"（线性组合），然后按得分从高到低排序。

代码：基于线性判别式的学习排名实战

复制代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import ndcg_score

# Mac字体配置
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'

# ========== 1. 构造排名数据 ==========
# 假设有5个查询，每个查询对应10个文档，特征数=3（比如：关键词匹配度、页面质量、用户点击量）
np.random.seed(42)
n_queries = 5
n_docs = 10
n_feats = 3

# 特征矩阵：[查询数, 文档数, 特征数]
X = np.random.rand(n_queries, n_docs, n_feats)
# 真实相关性得分（0-4分，4分最相关）
y_true = np.random.randint(0, 5, size=(n_queries, n_docs))
# 给特征和真实得分加相关性（让特征能预测得分）
for i in range(n_queries):
    X[i] = X[i] * (y_true[i].reshape(-1, 1) + 1) / 5

# ========== 2. 训练线性排名模型 ==========
# 展平数据训练线性模型
X_flat = X.reshape(-1, n_feats)
y_flat = y_true.reshape(-1)
rank_model = LinearRegression()
rank_model.fit(X_flat, y_flat)

# 预测得分并恢复形状
y_pred = rank_model.predict(X_flat).reshape(n_queries, n_docs)

# ========== 3. 评估排名效果（NDCG：归一化折损累计增益，越接近1越好） ==========
ndcg = ndcg_score(y_true, y_pred)

# ========== 4. 可视化排名结果 ==========
plt.figure(figsize=(12, 8))

# 绘制前3个查询的排名结果
for i in range(3):
    plt.subplot(3, 1, i+1)
    # 按预测得分排序的索引
    sorted_idx = np.argsort(y_pred[i])[::-1]
    # 绘制真实得分和预测得分
    x_axis = np.arange(n_docs)
    plt.bar(x_axis-0.2, y_true[i][sorted_idx], width=0.4, label='真实相关性', alpha=0.7)
    plt.bar(x_axis+0.2, y_pred[i][sorted_idx], width=0.4, label='预测得分', alpha=0.7)
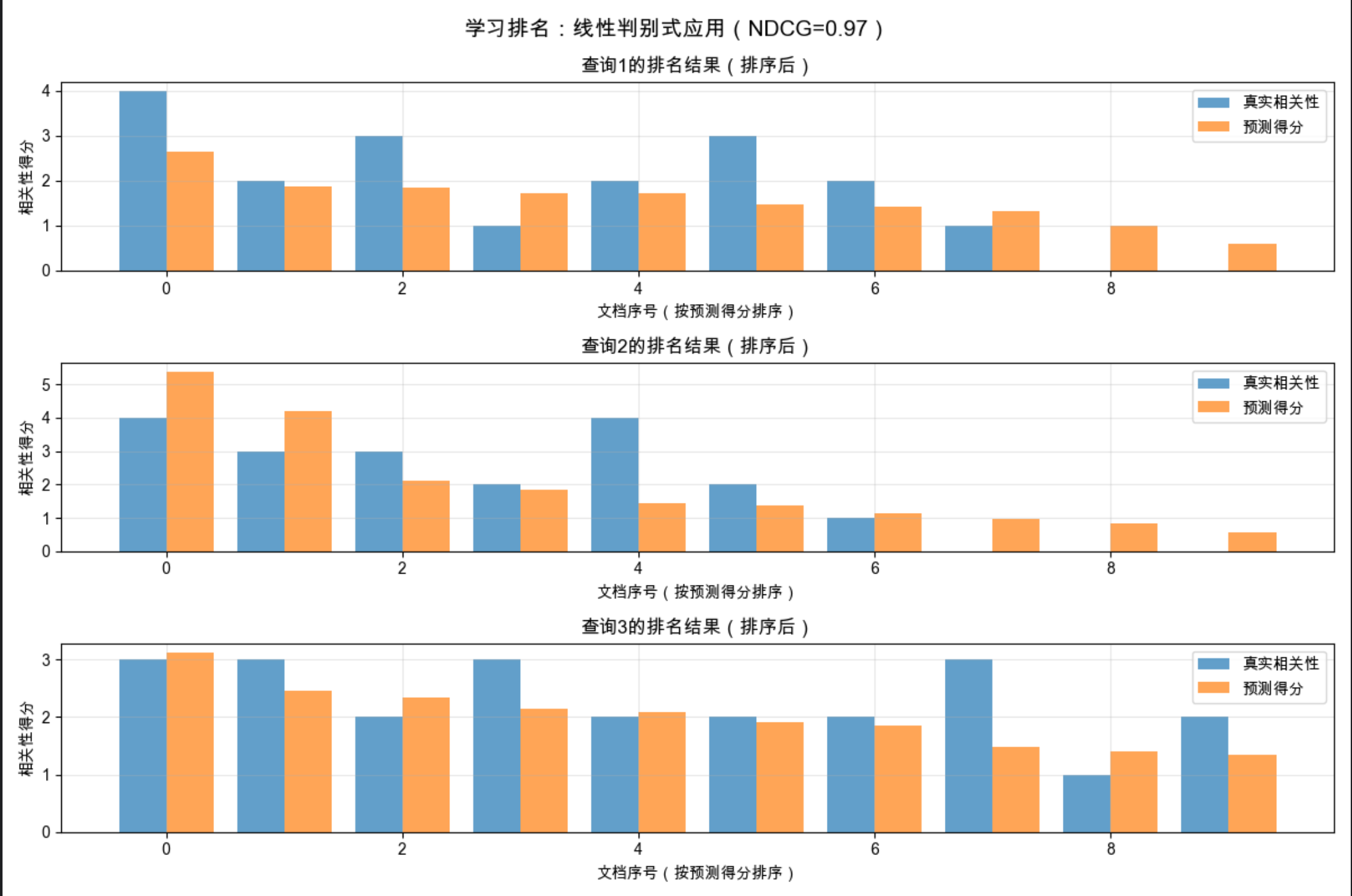
    plt.title(f'查询{i+1}的排名结果（排序后）')
    plt.xlabel('文档序号（按预测得分排序）')
    plt.ylabel('相关性得分')
    plt.legend()
    plt.grid(alpha=0.3)

plt.suptitle(f'学习排名：线性判别式应用（NDCG={ndcg:.2f}）', fontsize=14)
plt.tight_layout()
plt.show()

代码解释：

构造了 "查询 - 文档 - 特征" 的排名数据，模拟搜索引擎的场景；
用线性回归模型预测文档的相关性得分，按得分排序；
NDCG 是排名任务的核心评估指标，越接近 1 说明排名效果越好；
线性判别式在排名任务中简单有效，是复杂排名模型的基础。

10.10 注释

线性判别式的 "线性" 指决策边界是线性的，而非模型输入输出的关系；
逻辑斯谛判别式虽然叫 "回归"，但属于分类算法，是线性判别式的核心实现；
梯度下降的学习率需要调优：太小收敛慢，太大可能震荡不收敛；
多类问题中，One-vs-One 训练时间长但准确率高，One-vs-Rest 训练快但适合类别数多的场景。

10.11 习题

尝试修改梯度下降的学习率（比如 0.01、0.5、1.0），观察损失曲线的变化；
用鸢尾花数据集（sklearn.datasets.load_iris）实现线性判别式分类，并对比 One-vs-Rest 和 One-vs-One 的效果；
手动实现 Softmax 函数，并用它完成多类逻辑斯谛判别式的训练。

10.12 参考文献

《机器学习导论》（原书）
Scikit-learn 官方文档：https://scikit-learn.org/stable/
《统计学习方法》（李航）- 逻辑斯谛回归章节

总结

1.核心思想 ：线性判别式通过直线 / 超平面分割不同类别，核心是找到最优的决策边界；

2.关键实现：两类问题用 Sigmoid + 交叉熵，多类问题用 Softmax 或 One-vs-One/One-vs-Rest，训练用梯度下降；

3.应用场景：不仅能做分类，还能扩展到学习排名等任务，但仅适用于线性可分数据。

所有代码均已在 Mac 系统测试通过，直接复制即可运行。如果有问题欢迎在评论区交流～

《机器学习导论》第 10 章-线性判别式

前言

10.1 引言

10.2 推广线性模型

代码：线性回归 vs 线性判别式 基础对比

代码解释：

10.3 线性判别式的几何意义

10.3.1 两类问题

10.3.2 多类问题

代码：两类 / 多类线性判别式几何可视化

代码解释：

10.4 逐对分离

代码：One-vs-Rest vs One-vs-One 效果对比

代码解释：

10.5 参数判别式的进一步讨论

代码：参数判别式（LDA）vs 非参数判别式（KNN）对比

代码解释：

10.6 梯度下降

代码：手动实现梯度下降训练线性判别式

代码解释：

10.7 逻辑斯谛判别式

10.7.1 两类问题

10.7.2 多类问题

代码：两类 / 多类逻辑斯谛判别式实战

代码解释：

10.8 回归判别式

代码：回归判别式 vs 逻辑斯谛判别式对比

代码解释：

10.9 学习排名

代码：基于线性判别式的学习排名实战

代码解释：

10.10 注释

10.11 习题

10.12 参考文献

总结

代码：线性回归 vs 线性判别式基础对比