基于最小二乘法的离散数据拟合

- [1. 拟合目标](#1. 拟合目标)
- [2. 最小二乘原理](#2. 最小二乘原理)
- - [2.1 问题设定](#2.1 问题设定)
  - [2.2 矩阵形式表示](#2.2 矩阵形式表示)
  - [2.3 目标函数展开](#2.3 目标函数展开)
  - [2.4 梯度计算](#2.4 梯度计算)
  - - [引理 1（线性项）：](#引理 1（线性项）：)
    - [引理 2（二次型）：](#引理 2（二次型）：)
  - [2.5 正规方程的导出](#2.5 正规方程的导出)
  - [2.6 解的存在性与数值求解](#2.6 解的存在性与数值求解)
- [3. 误差评估](#3. 误差评估)
- [4. Python 实现详解](#4. Python 实现详解)
- [5. 运行结果示例](#5. 运行结果示例)
附：文章说明

在实际应用中，我们常常无法获得函数的完整解析表达式，而只能通过实验、测量或采样等方式获得一组离散数据点 { ( x i , y i ) } i = 0 n \{(x_i, y_i)\}_{i=0}^{n} {(xi,yi)}i=0n。此时，可用最小二乘拟合（Least Squares Fitting）来近似描述这些数据的整体趋势。

最小二乘法的目标是：在所有次数不超过 k k k 的多项式中，找到一个 p k ( x ) p_k(x) pk(x)，使得其在所有采样点上的平方残差和最小，即最小化如下目标函数：

S = ∑ i = 0 n ( y i − p k ( x i ) ) 2 . S = \sum_{i=0}^{n} \bigl( y_i - p_k(x_i) \bigr)^2. S=i=0∑n(yi−pk(xi))2.

与最佳平方逼近 （针对连续函数、使用积分误差）不同，最小二乘拟合处理的是离散数据。

在实现上，最小二乘拟合通常通过求解正规方程组 （Normal Equations）来获得多项式系数。为提高数值稳定性，也可以采用正交基 （如离散勒让德基）进行拟合。本文采用标准幂基 { 1 , x , x 2 , ... , x k } \{1, x, x^2, \dots, x^k\} {1,x,x2,...,xk}。

1. 拟合目标

给定目标函数（用于生成采样数据）：

f ( x ) = 1 1 + c x 2 f(x) = \frac{1}{1 + c x^2} f(x)=1+cx21

在区间 [ a , b ] [a, b] [a,b] 上均匀采样 n + 1 n+1 n+1 个点：

x i = a + i ⋅ b − a n , y i = f ( x i ) , i = 0 , 1 , ... , n . x_i = a + i \cdot \frac{b - a}{n}, \quad y_i = f(x_i), \quad i = 0, 1, \dots, n. xi=a+i⋅nb−a,yi=f(xi),i=0,1,...,n.

目标是构造一个次数不超过 k k k 的多项式：

p k ( x ) = ∑ j = 0 k α j x j p_k(x) = \sum_{j=0}^{k} \alpha_j x^j pk(x)=j=0∑kαjxj

使得其在这些数据点上满足最小二乘准则。

当然可以。以下是对 "最小二乘原理" 的完整、严谨、自包含的推导，从问题设定、目标函数构建，到矩阵形式表达，再到梯度计算与正规方程的导出，每一步都力求清晰、严密、无跳跃。

2. 最小二乘原理

2.1 问题设定

给定一组离散观测数据：
{ ( x i , y i ) } i = 0 n , x i ∈ R , y i ∈ R , \{(x_i, y_i)\}_{i=0}^{n}, \quad x_i \in \mathbb{R}, \; y_i \in \mathbb{R}, {(xi,yi)}i=0n,xi∈R,yi∈R,

我们希望寻找一个次数不超过 k k k 的多项式：
p k ( x ) = α 0 + α 1 x + α 2 x 2 + ⋯ + α k x k = ∑ j = 0 k α j x j , p_k(x) = \alpha_0 + \alpha_1 x + \alpha_2 x^2 + \cdots + \alpha_k x^k = \sum_{j=0}^{k} \alpha_j x^j, pk(x)=α0+α1x+α2x2+⋯+αkxk=j=0∑kαjxj,

使得该多项式在所有数据点上"整体上最接近"观测值 y i y_i yi。

由于通常无法使 p k ( x i ) = y i p_k(x_i) = y_i pk(xi)=yi 对所有 i i i 成立（尤其是当 k < n k < n k<n 时），我们转而采用最小二乘准则：最小化所有残差的平方和。

定义残差为：
r i = y i − p k ( x i ) , i = 0 , 1 , ... , n . r_i = y_i - p_k(x_i), \quad i = 0, 1, \dots, n. ri=yi−pk(xi),i=0,1,...,n.

目标是最小化如下平方误差和 ：
S ( α ) = ∑ i = 0 n ( y i − p k ( x i ) ) 2 = ∑ i = 0 n ( y i − ∑ j = 0 k α j x i j ) 2 , S(\boldsymbol{\alpha}) = \sum_{i=0}^{n} \bigl( y_i - p_k(x_i) \bigr)^2 = \sum_{i=0}^{n} \left( y_i - \sum_{j=0}^{k} \alpha_j x_i^j \right)^2, S(α)=i=0∑n(yi−pk(xi))2=i=0∑n(yi−j=0∑kαjxij)2,

其中 α = [ α 0 , α 1 , ... , α k ] ⊤ ∈ R k + 1 \boldsymbol{\alpha} = [\alpha_0, \alpha_1, \dots, \alpha_k]^\top \in \mathbb{R}^{k+1} α=[α0,α1,...,αk]⊤∈Rk+1 是待求系数向量。

2.2 矩阵形式表示

为便于分析，我们将上述求和式写成矩阵形式。

定义设计矩阵 （也称 Vandermonde 矩阵） A ∈ R ( n + 1 ) × ( k + 1 ) \mathbf{A} \in \mathbb{R}^{(n+1) \times (k+1)} A∈R(n+1)×(k+1) 为：
A i j = x i j , i = 0 , 1 , ... , n ; j = 0 , 1 , ... , k . \mathbf{A}_{ij} = x_i^j, \quad i = 0, 1, \dots, n; \quad j = 0, 1, \dots, k. Aij=xij,i=0,1,...,n;j=0,1,...,k.

即：
A = [ 1 x 0 x 0 2 ⋯ x 0 k 1 x 1 x 1 2 ⋯ x 1 k ⋮ ⋮ ⋮ ⋱ ⋮ 1 x n x n 2 ⋯ x n k ] . \mathbf{A} = \begin{bmatrix} 1 & x_0 & x_0^2 & \cdots & x_0^k \\ 1 & x_1 & x_1^2 & \cdots & x_1^k \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_n & x_n^2 & \cdots & x_n^k \end{bmatrix}. A= 11⋮1x0x1⋮xnx02x12⋮xn2⋯⋯⋱⋯x0kx1k⋮xnk .

定义观测向量 y ∈ R n + 1 \mathbf{y} \in \mathbb{R}^{n+1} y∈Rn+1 和系数向量 α ∈ R k + 1 \boldsymbol{\alpha} \in \mathbb{R}^{k+1} α∈Rk+1 为：
y = [ y 0 y 1 ⋮ y n ] , α = [ α 0 α 1 ⋮ α k ] . \mathbf{y} = \begin{bmatrix} y_0 \\ y_1 \\ \vdots \\ y_n \end{bmatrix}, \quad \boldsymbol{\alpha} = \begin{bmatrix} \alpha_0 \\ \alpha_1 \\ \vdots \\ \alpha_k \end{bmatrix}. y= y0y1⋮yn ,α= α0α1⋮αk .

则多项式在所有数据点上的预测值可表示为：
A α = [ p k ( x 0 ) p k ( x 1 ) ⋮ p k ( x n ) ] . \mathbf{A} \boldsymbol{\alpha} = \begin{bmatrix} p_k(x_0) \\ p_k(x_1) \\ \vdots \\ p_k(x_n) \end{bmatrix}. Aα= pk(x0)pk(x1)⋮pk(xn) .

残差向量为：
r = y − A α ∈ R n + 1 . \mathbf{r} = \mathbf{y} - \mathbf{A} \boldsymbol{\alpha} \in \mathbb{R}^{n+1}. r=y−Aα∈Rn+1.

于是，平方误差和可写为欧几里得范数的平方：
S ( α ) = ∥ r ∥ 2 2 = ( y − A α ) ⊤ ( y − A α ) . S(\boldsymbol{\alpha}) = \|\mathbf{r}\|_2^2 = (\mathbf{y} - \mathbf{A} \boldsymbol{\alpha})^\top (\mathbf{y} - \mathbf{A} \boldsymbol{\alpha}). S(α)=∥r∥22=(y−Aα)⊤(y−Aα).

2.3 目标函数展开

展开 S ( α ) S(\boldsymbol{\alpha}) S(α)：
S ( α ) = ( y − A α ) ⊤ ( y − A α ) = y ⊤ y − y ⊤ A α − α ⊤ A ⊤ y + α ⊤ A ⊤ A α . \begin{aligned} S(\boldsymbol{\alpha}) &= (\mathbf{y} - \mathbf{A} \boldsymbol{\alpha})^\top (\mathbf{y} - \mathbf{A} \boldsymbol{\alpha}) \\ &= \mathbf{y}^\top \mathbf{y} - \mathbf{y}^\top \mathbf{A} \boldsymbol{\alpha} - \boldsymbol{\alpha}^\top \mathbf{A}^\top \mathbf{y} + \boldsymbol{\alpha}^\top \mathbf{A}^\top \mathbf{A} \boldsymbol{\alpha}. \end{aligned} S(α)=(y−Aα)⊤(y−Aα)=y⊤y−y⊤Aα−α⊤A⊤y+α⊤A⊤Aα.

注意到 y ⊤ A α \mathbf{y}^\top \mathbf{A} \boldsymbol{\alpha} y⊤Aα 是一个标量，标量的转置等于自身，因此：
y ⊤ A α = ( y ⊤ A α ) ⊤ = α ⊤ A ⊤ y . \mathbf{y}^\top \mathbf{A} \boldsymbol{\alpha} = (\mathbf{y}^\top \mathbf{A} \boldsymbol{\alpha})^\top = \boldsymbol{\alpha}^\top \mathbf{A}^\top \mathbf{y}. y⊤Aα=(y⊤Aα)⊤=α⊤A⊤y.

故两项合并：
S ( α ) = y ⊤ y − 2 α ⊤ A ⊤ y + α ⊤ A ⊤ A α . S(\boldsymbol{\alpha}) = \mathbf{y}^\top \mathbf{y} - 2 \boldsymbol{\alpha}^\top \mathbf{A}^\top \mathbf{y} + \boldsymbol{\alpha}^\top \mathbf{A}^\top \mathbf{A} \boldsymbol{\alpha}. S(α)=y⊤y−2α⊤A⊤y+α⊤A⊤Aα.

2.4 梯度计算

为求 S ( α ) S(\boldsymbol{\alpha}) S(α) 的最小值，我们对其关于 α \boldsymbol{\alpha} α 求梯度，并令其为零向量。

我们采用分子布局 （numerator layout），即梯度 ∇ α f \nabla_{\boldsymbol{\alpha}} f ∇αf 为与 α \boldsymbol{\alpha} α 同维的列向量。

需要以下两个基本矩阵微分规则：

引理 1（线性项）：

若 b ∈ R k + 1 \mathbf{b} \in \mathbb{R}^{k+1} b∈Rk+1 为常向量，则
∇ α ( α ⊤ b ) = b . \nabla_{\boldsymbol{\alpha}} (\boldsymbol{\alpha}^\top \mathbf{b}) = \mathbf{b}. ∇α(α⊤b)=b.
证明： α ⊤ b = ∑ j = 0 k α j b j \boldsymbol{\alpha}^\top \mathbf{b} = \sum_{j=0}^{k} \alpha_j b_j α⊤b=∑j=0kαjbj，对 α i \alpha_i αi 求偏导得 b i b_i bi，故梯度为 b \mathbf{b} b。

引理 2（二次型）：

若 M ∈ R ( k + 1 ) × ( k + 1 ) \mathbf{M} \in \mathbb{R}^{(k+1) \times (k+1)} M∈R(k+1)×(k+1) 为对称矩阵（即 M = M ⊤ \mathbf{M} = \mathbf{M}^\top M=M⊤），则
∇ α ( α ⊤ M α ) = 2 M α . \nabla_{\boldsymbol{\alpha}} (\boldsymbol{\alpha}^\top \mathbf{M} \boldsymbol{\alpha}) = 2 \mathbf{M} \boldsymbol{\alpha}. ∇α(α⊤Mα)=2Mα.
证明：展开 α ⊤ M α = ∑ i , j α i M i j α j \boldsymbol{\alpha}^\top \mathbf{M} \boldsymbol{\alpha} = \sum_{i,j} \alpha_i M_{ij} \alpha_j α⊤Mα=∑i,jαiMijαj，对 α k \alpha_k αk 求偏导：
∂ ∂ α k ∑ i , j α i M i j α j = ∑ j M k j α j + ∑ i α i M i k = ( M α ) k + ( M ⊤ α ) k . \frac{\partial}{\partial \alpha_k} \sum_{i,j} \alpha_i M_{ij} \alpha_j = \sum_j M_{kj} \alpha_j + \sum_i \alpha_i M_{ik} = (\mathbf{M} \boldsymbol{\alpha})_k + (\mathbf{M}^\top \boldsymbol{\alpha})_k. ∂αk∂i,j∑αiMijαj=j∑Mkjαj+i∑αiMik=(Mα)k+(M⊤α)k.

若 M = M ⊤ \mathbf{M} = \mathbf{M}^\top M=M⊤，则两项相等，结果为 2 ( M α ) k 2 (\mathbf{M} \boldsymbol{\alpha})_k 2(Mα)k。故梯度为 2 M α 2 \mathbf{M} \boldsymbol{\alpha} 2Mα。

注：此处 A ⊤ A \mathbf{A}^\top \mathbf{A} A⊤A 恒为对称矩阵，因为 ( A ⊤ A ) ⊤ = A ⊤ ( A ⊤ ) ⊤ = A ⊤ A (\mathbf{A}^\top \mathbf{A})^\top = \mathbf{A}^\top (\mathbf{A}^\top)^\top = \mathbf{A}^\top \mathbf{A} (A⊤A)⊤=A⊤(A⊤)⊤=A⊤A。

现在对 S ( α ) S(\boldsymbol{\alpha}) S(α) 求梯度：
S ( α ) = y ⊤ y − 2 α ⊤ A ⊤ y + α ⊤ A ⊤ A α . S(\boldsymbol{\alpha}) = \mathbf{y}^\top \mathbf{y} - 2 \boldsymbol{\alpha}^\top \mathbf{A}^\top \mathbf{y} + \boldsymbol{\alpha}^\top \mathbf{A}^\top \mathbf{A} \boldsymbol{\alpha}. S(α)=y⊤y−2α⊤A⊤y+α⊤A⊤Aα.

∇ α ( y ⊤ y ) = 0 \nabla_{\boldsymbol{\alpha}} (\mathbf{y}^\top \mathbf{y}) = \mathbf{0} ∇α(y⊤y)=0（常数）；
∇ α ( − 2 α ⊤ A ⊤ y ) = − 2 A ⊤ y \nabla_{\boldsymbol{\alpha}} (-2 \boldsymbol{\alpha}^\top \mathbf{A}^\top \mathbf{y}) = -2 \mathbf{A}^\top \mathbf{y} ∇α(−2α⊤A⊤y)=−2A⊤y（由引理 1）；
∇ α ( α ⊤ A ⊤ A α ) = 2 A ⊤ A α \nabla_{\boldsymbol{\alpha}} (\boldsymbol{\alpha}^\top \mathbf{A}^\top \mathbf{A} \boldsymbol{\alpha}) = 2 \mathbf{A}^\top \mathbf{A} \boldsymbol{\alpha} ∇α(α⊤A⊤Aα)=2A⊤Aα（由引理 2，因 A ⊤ A \mathbf{A}^\top \mathbf{A} A⊤A 对称）。

因此：
∇ α S ( α ) = − 2 A ⊤ y + 2 A ⊤ A α . \nabla_{\boldsymbol{\alpha}} S(\boldsymbol{\alpha}) = -2 \mathbf{A}^\top \mathbf{y} + 2 \mathbf{A}^\top \mathbf{A} \boldsymbol{\alpha}. ∇αS(α)=−2A⊤y+2A⊤Aα.

2.5 正规方程的导出

令梯度为零向量以寻找极小值点：
∇ α S ( α ) = 0 ⇒ − 2 A ⊤ y + 2 A ⊤ A α = 0. \nabla_{\boldsymbol{\alpha}} S(\boldsymbol{\alpha}) = \mathbf{0} \quad \Rightarrow \quad -2 \mathbf{A}^\top \mathbf{y} + 2 \mathbf{A}^\top \mathbf{A} \boldsymbol{\alpha} = \mathbf{0}. ∇αS(α)=0⇒−2A⊤y+2A⊤Aα=0.

两边除以 2，整理得：
A ⊤ A α = A ⊤ y . \mathbf{A}^\top \mathbf{A} \boldsymbol{\alpha} = \mathbf{A}^\top \mathbf{y}. A⊤Aα=A⊤y.

该线性方程组称为正规方程（Normal Equations）。

2.6 解的存在性与数值求解

若 A \mathbf{A} A 列满秩（即 rank ( A ) = k + 1 \text{rank}(\mathbf{A}) = k+1 rank(A)=k+1，通常当 n ≥ k n \ge k n≥k 且采样点 x i x_i xi 互异时成立），则 A ⊤ A \mathbf{A}^\top \mathbf{A} A⊤A 可逆，正规方程有唯一解：
α = ( A ⊤ A ) − 1 A ⊤ y . \boldsymbol{\alpha} = (\mathbf{A}^\top \mathbf{A})^{-1} \mathbf{A}^\top \mathbf{y}. α=(A⊤A)−1A⊤y.

3. 误差评估

为客观评估拟合质量，我们在区间内随机生成 m m m 个测试点 { x j test } j = 1 m \{x^{\text{test}}j\}{j=1}^m {xjtest}j=1m，计算：

真实值： y j true = f ( x j test ) y^{\text{true}}_j = f(x^{\text{test}}_j) yjtrue=f(xjtest)
拟合值： y j fit = p k ( x j test ) y^{\text{fit}}_j = p_k(x^{\text{test}}_j) yjfit=pk(xjtest)

并计算平均绝对误差（MAE）：

MAE = 1 m ∑ j = 1 m ∣ y j fit − y j true ∣ . \text{MAE} = \frac{1}{m} \sum_{j=1}^{m} \big| y^{\text{fit}}_j - y^{\text{true}}_j \big|. MAE=m1j=1∑m yjfit−yjtrue .

4. Python 实现详解

python 复制代码

# coding=utf-8
import os
import numpy as np
import matplotlib.pyplot as plt
import matplotlib

matplotlib.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['axes.unicode_minus'] = False

# ========== 配置参数 ==========
INTERVAL = (-1.0, 1.0)      # 采样区间 [a, b]
C = 1.0                     # 目标函数 f(x) = 1/(1 + C * x^2)
N = 10                      # 采样点数 = N + 1
K = 3                       # 拟合多项式次数（0 <= K <= N）
M = 100                     # 随机误差评估点数
RESULT_DIR = 输出目录

# ========== 目标函数 ==========
def f(x):
    return 1.0 / (1.0 + C * x**2)

# ========== 生成采样数据 ==========
def generate_data():
    a, b = INTERVAL
    x_vals = np.linspace(a, b, N + 1)
    y_vals = f(x_vals)
    return x_vals, y_vals

# ========== 构造设计矩阵 ==========
def design_matrix(x, k):
    """
    构造 Vandermonde 矩阵：A[i, j] = x[i]^j
    """
    return np.vander(x, k + 1, increasing=True)

# ========== 最小二乘拟合 ==========
def least_squares_fit(x_data, y_data, k):
    A = design_matrix(x_data, k)
    # 使用 lstsq 避免显式求解正规方程（更稳定）
    coeffs, residuals, rank, s = np.linalg.lstsq(A, y_data, rcond=None)
    return coeffs

# ========== 拟合函数求值 ==========
def evaluate_fit(coeffs, x_query):
    return np.polyval(coeffs[::-1], x_query)  # coeffs 按 0~k 次排列，需反转用于 polyval

# ========== 打印拟合多项式表达式 ==========
def print_fit_polynomial(coeffs, max_terms=15):
    terms = []
    for j, coeff in enumerate(coeffs):
        if max_terms and j >= max_terms:
            terms.append("...")
            break
        c_str = f"{coeff:+.6f}"
        if j == 0:
            term = f"{c_str}"
        elif j == 1:
            term = f"{c_str}*x"
        else:
            term = f"{c_str}*x^{j}"
        terms.append(term)
    expr = " ".join(terms).lstrip('+ ')
    expr = expr.replace('+ -', '- ')
    print("最小二乘拟合多项式表达式：")
    print(f"f(x) ≈ {expr}")
    print("-" * 80)

# ========== 主程序 ==========
def main():
    os.makedirs(RESULT_DIR, exist_ok=True)
    a, b = INTERVAL

    # 生成数据
    x_data, y_data = generate_data()

    # 执行最小二乘拟合
    coeffs = least_squares_fit(x_data, y_data, K)

    # 高密度绘图
    x_plot = np.linspace(a, b, 1000)
    y_true = f(x_plot)
    y_fit = evaluate_fit(coeffs, x_plot)

    # 随机测试点评估 MAE
    x_test = np.random.uniform(a, b, M)
    y_true_test = f(x_test)
    y_fit_test = evaluate_fit(coeffs, x_test)
    mae = np.mean(np.abs(y_fit_test - y_true_test))

    # 输出结果
    print(f"最小二乘拟合的平均绝对误差 (MAE): {mae:.6f}\n")
    print_fit_polynomial(coeffs)

    # 绘图
    plt.figure(figsize=(12, 6))
    plt.plot(x_plot, y_true, 'k-', label=r'真实函数 $f(x) = \frac{1}{1 + C x^2}$')
    plt.plot(x_plot, y_fit, 'b--', label=f'最小二乘拟合 (K={K})')
    plt.scatter(x_data, y_data, color='red', s=40, zorder=5, label='采样数据点')
    plt.grid(True, linestyle=':', alpha=0.7)
    plt.legend()
    plt.title(f'最小二乘拟合（采样点数={N+1}, 拟合次数={K}, MAE={mae:.4f}）')
    plt.xlabel('x')
    plt.ylabel('y')
    plt.tight_layout()

    plot_path = os.path.join(RESULT_DIR, 'least_squares_fit.png')
    plt.savefig(plot_path, dpi=300)
    print(f"结果图已保存至: {plot_path}")
    plt.show()

if __name__ == '__main__':
    main()

5. 运行结果示例

最小二乘拟合的平均绝对误差 (MAE): 0.029532

最小二乘拟合多项式表达式：
f ( x ) ≈ 0.953812 − 0.000000 ∗ x − 0.489686 ∗ x 2 + 0.000000 ∗ x 3 f(x) ≈ 0.953812 -0.000000*x -0.489686*x^{2}+0.000000*x^{3} f(x)≈0.953812−0.000000∗x−0.489686∗x2+0.000000∗x3

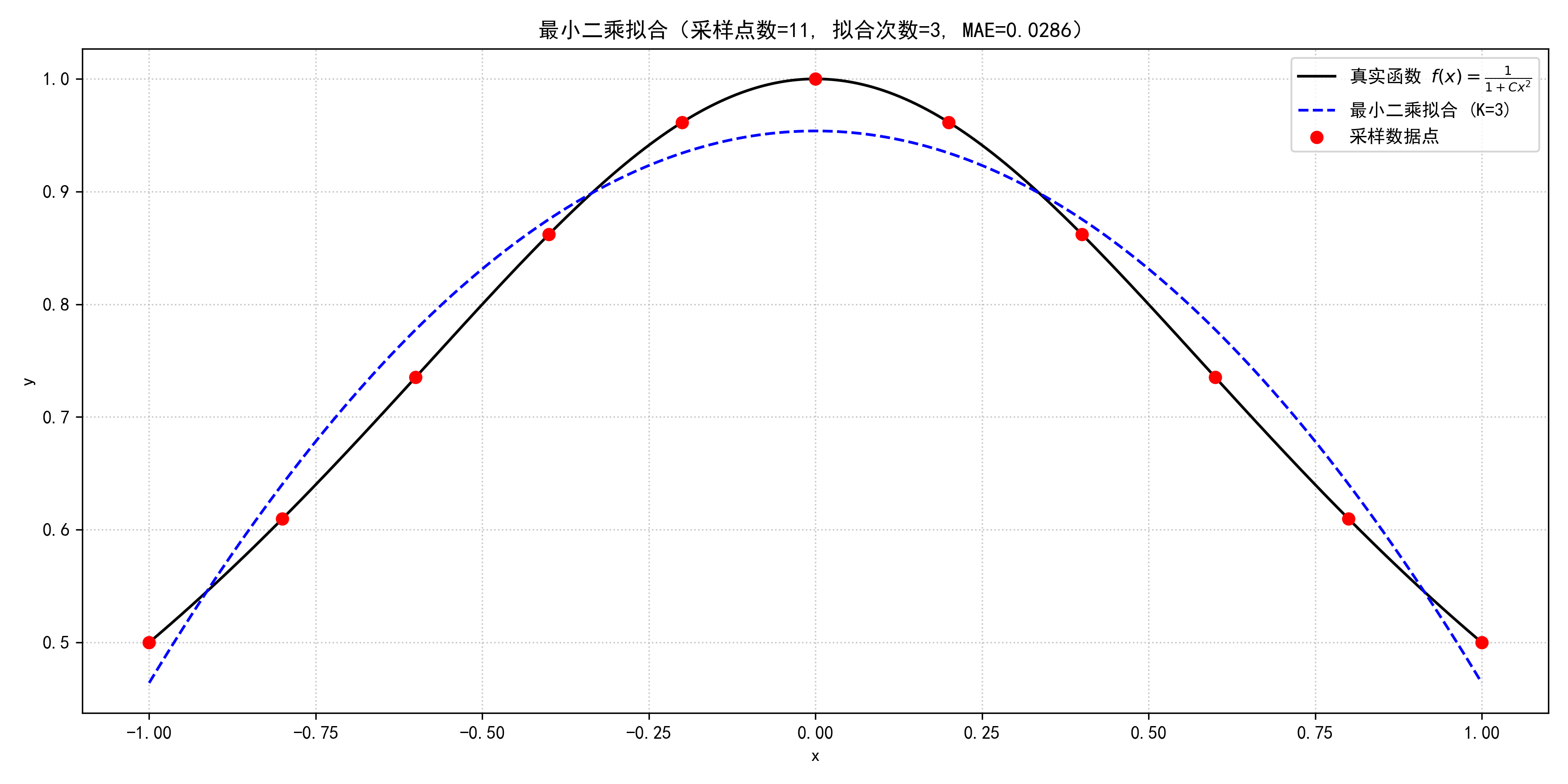
注：由于采样点对称且目标函数为偶函数，奇次项系数趋近于零，符合预期。

附：文章说明

本文仅为个人理解，若有不当之处，欢迎指正～