多臂老虎机算法（Multi-Armed Bandit, MAB）详解

多臂老虎机算法（Multi-Armed Bandit, MAB）详解

多臂老虎机算法是一类在线学习算法 ，核心解决 "探索 - 利用权衡"（Exploration-Exploitation Tradeoff）问题 ------ 在不确定每个选项（"臂"）收益分布的情况下，通过动态选择策略最大化长期累积收益。它广泛应用于推荐系统、A/B 测试、路径优化、资源分配等场景，尤其适合数据稀疏、需要实时决策的场景（如你的运输路线规划中，动态选择最优路线 / 货运方式）。

本文将从 "基础概念→核心问题→经典算法→变种扩展→项目应用→代码实现" 逐步讲解，兼顾理论深度和工程实用性。

一、基础概念：什么是 "多臂老虎机"？

1.1 场景类比

想象你面前有 N 台老虎机（"多臂"），每台机器的中奖概率（或收益）不同，且你不知道具体分布。你的目标是通过多次拉杆（"决策"），最大化总收益 ------ 这就是多臂老虎机的核心场景：

• 臂（Arm）：可选的决策选项（如运输路线规划中的 "路线 A""路线 B""路线 C"，货运方式中的 "公路""铁路""海运"）。
• 收益（Reward）：选择某臂后获得的反馈（如路线的 "运输时间""成本""准时率"，可转化为量化收益，例如：准时率 90% 对应收益 0.9，延迟对应负收益）。
• 探索（Exploration）：尝试未选过或选择次数少的臂，获取更多收益分布信息（如尝试一条新的运输路线，了解其实际耗时）。
• 利用（Exploitation）：选择当前已知收益最高的臂，最大化即时收益（如一直走已知最快的路线）。

1.2 数学建模

• 设共有 K 个臂，第 i 个臂的收益服从分布\(R_i \sim P_i(r)\)（如伯努利分布：中奖 / 未中奖；高斯分布：运输时间的波动）。
• 每个臂的 "真实价值" 为期望收益：\(\mu_i = E[R_i]\)。
• 算法目标：通过 T 次决策（T 轮拉杆），选择序列\(a_1, a_2, ..., a_T\)（\(a_t \in \{1,2,...,K\}\)），最大化累积收益：\(\sum_{t=1}^T R(a_t)\)，或最小化 "累积遗憾"（Regret）：\(Regret(T) = T \cdot \mu^* - \sum_{t=1}^T \mu_{a_t}\)（\(\mu^*\)是所有臂的最大真实价值）。

二、核心问题：探索与利用的权衡

这是多臂老虎机的本质矛盾：

• 只 "利用"：一直选当前最优臂，可能错过更优的未知臂（如一直走老路，却不知道新路线更快），长期收益受限。
• 只 "探索"：频繁尝试新臂，牺牲即时收益，导致短期损失过大（如每次都试新路线，多次遇到拥堵）。

所有多臂老虎机算法的差异，本质是探索策略的设计------ 如何在 "获取信息" 和 "获取收益" 之间找到最优平衡。

三、经典多臂老虎机算法

3.1 贪心算法（Greedy）：纯 "利用"，无探索

原理

• 初始化：对每个臂尝试 m 次（m≥1），计算各臂的平均收益\(\hat{\mu}i = \frac{1}{m} \sum{k=1}^m R_i^k\)。
• 决策：之后每一轮都选择当前平均收益最高的臂（若有多个，随机选一个）。
• 变种："纯贪心"（m=1，仅尝试一次就固定选择）。

公式

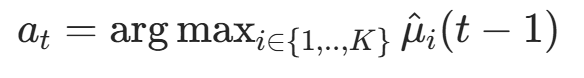
是前 t-1 轮中臂 i 的平均收益

优缺点

• 优点：实现最简单，计算成本低，短期收益稳定。
• 缺点：完全没有探索，若初始尝试次数 m 不足，可能锁定次优臂（如初始尝试新路线时刚好遇到拥堵，误判为差路线），长期遗憾会随 T 线性增长（Regret(T) ∝ T）。

适用场景

• 收益分布稳定、初始数据充足，且不担心错过最优臂的场景（不推荐用于运输路线规划，因路线收益受路况、天气影响，需动态探索）。

3.2 ε- 贪心算法（ε-Greedy）：固定概率探索

原理

在贪心算法基础上引入 "探索概率 ε"（0<ε<1），平衡探索与利用：

• 每一轮决策时，以概率\(1-\varepsilon\)选择当前最优臂（利用）；
• 以概率\(\varepsilon\)随机选择一个臂（探索，不管当前收益高低）。
• 变种：衰减 ε- 贪心（\(\varepsilon(t) = \frac{1}{\sqrt{t}}\)或\(\varepsilon(t) = \frac{\varepsilon_0}{t}\)），随着轮次 t 增加，探索概率逐渐降低（符合 "初期多探索，后期多利用" 的直觉）。

公式

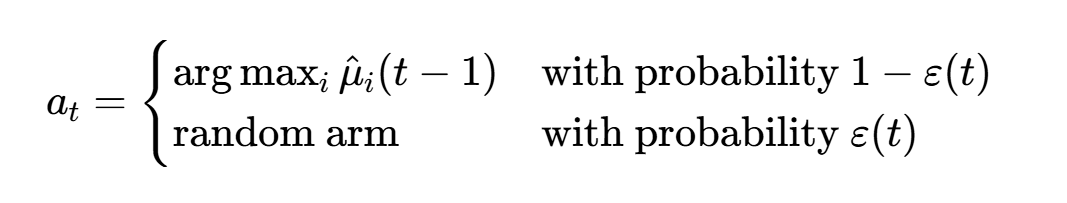
优缺点

• 优点：实现简单，探索策略可控，长期遗憾优于纯贪心（Regret(T) ∝ √T，亚线性增长）。
• 缺点：探索是"盲目的"（随机选臂，可能重复探索差臂），ε的取值需要人工调参（如ε=0.1适合初期，ε=0.01适合后期）。

适用场景

• 快速验证场景、对调参不敏感的简单决策问题（如运输路线初期筛选，快速排除明显差路线）。

3.3 上置信界算法（Upper Confidence Bound, UCB）："乐观估计"的探索

核心思想

"不确定即探索"------对每个臂的收益估计加入置信区间，优先选择"置信区间上界最高"的臂（既考虑当前平均收益，也考虑选择次数：选择次数越少，置信区间越宽，上界越高，越容易被选中探索）。

经典变种：UCB1（最常用）

• 初始化：每个臂至少尝试1次（确保\(\hat{\mu}_i\)有定义）。
• 第t轮（t≥K+1），对每个臂i，计算UCB值：\(UCB_i(t) = \hat{\mu}_i(t-1) + \sqrt{\frac{2 \ln t}{n_i(t-1)}}\)其中：
  • \(\hat{\mu}_i(t-1)\)：臂i的历史平均收益；
  • \(n_i(t-1)\)：臂i的历史选择次数；
  • \(\sqrt{\frac{2 \ln t}{n_i(t-1)}}\)：置信区间项（t越大、n_i越小，该项越大，鼓励探索）。
• 决策：选择UCB值最高的臂。

优缺点

• 优点：探索有"方向性"（优先探索"可能是最优"的臂，而非随机探索），无需调参，长期遗憾最优（Regret(T) ∝ √(KT ln T)）。
• 缺点：计算量略高于贪心，对收益分布的"乐观估计"可能导致初期探索过多（如对完全未知的臂，UCB值极高，频繁选择）。

适用场景

• 收益分布稳定、需要自动平衡探索与利用的场景（强烈推荐用于运输路线规划的基础算法，如固定路线集的动态选择）。

3.4 汤普森采样（Thompson Sampling, TS）：基于贝叶斯的概率探索

核心思想

"贝叶斯后验推断"------对每个臂的收益分布建模（如伯努利分布对应二分类收益，高斯分布对应连续收益），每轮通过后验分布采样一个"虚拟收益"，选择采样值最高的臂。

算法步骤（以伯努利收益为例，如"准时=1，延迟=0"）

1. 初始化：每个臂i对应Beta分布的参数（α_i=1，β_i=1）（Beta分布是伯努利分布的共轭先验，计算简便）。
2. 第t轮：
   • 对每个臂i，从Beta(α_i, β_i)中采样一个值\(\theta_i\)（代表当前对臂i中奖概率的信念）；
   • 选择\(\theta_i\)最大的臂i作为决策；
   • 观察实际收益r（1或0），更新参数：若r=1则α_i +=1，若r=0则β_i +=1。
3. 重复步骤2，随着数据增多，后验分布逐渐收敛到真实收益分布。

公式（伯努利场景）

• 后验分布：\(P(\mu_i | 数据) = Beta(\alpha_i, \beta_i)\)，其中α_i = 成功次数+1，β_i = 失败次数+1；
• 采样与决策：\(a_t = \arg\max_{i} \theta_i\)（\(\theta_i \sim Beta(\alpha_i, \beta_i)\)）。

优缺点

• 优点：
  1. 探索更"智能"（基于概率信念，优先探索"不确定性高且潜在收益高"的臂）；
  2. 天然支持"上下文信息"（如结合天气、路况、时间段等，扩展为上下文多臂老虎机）；
  3. 计算量小（采样操作高效），长期遗憾与UCB相当。
• 缺点：需要先假设收益分布（如伯努利、高斯），若假设与实际分布偏差大，性能会下降（可通过非参数方法缓解）。

适用场景

• 收益分布可建模、需要精准探索的场景（最推荐用于运输路线规划，如结合路况上下文、收益分布（运输时间/成本）建模）。

四、变种与扩展：适配复杂场景

4.1 上下文多臂老虎机（Contextual MAB, CMAB）

核心改进

传统MAB忽略"决策上下文"（如运输路线选择时，"天气""时间段""货物类型"都是上下文），CMAB将上下文信息融入决策，每个"臂+上下文"组合视为一个独立的决策单元。

应用场景（运输路线规划）

• 上下文：天气（晴/雨/雪）、时间段（早高峰/晚高峰/平峰）、货物紧急程度（紧急/普通）；
• 决策：对"路线A+早高峰+雨天""路线B+平峰+晴天"等不同组合，分别学习最优收益，动态选择适配当前上下文的路线。

经典算法

• LinUCB（线性上下文UCB）：假设收益与上下文呈线性关系，适用于连续型上下文；
• Thompson Sampling with Context：将上下文作为特征融入后验分布建模（如用逻辑回归预测收益）。

4.2 多目标多臂老虎机（Multi-Objective MAB）

核心改进

传统MAB仅优化单一收益目标（如"最小化运输时间"），多目标MAB同时优化多个冲突目标（如"最小化时间""最小化成本""最大化准时率"），输出帕累托最优解。

应用场景（运输路线规划）

• 目标1：运输时间最短；
• 目标2：运输成本最低；
• 目标3：准时率最高；
• 算法：通过加权求和（将多目标转化为单目标）或帕累托排序（选择非支配解）实现决策。

4.3 非平稳多臂老虎机（Non-Stationary MAB）

核心改进

传统MAB假设收益分布固定，非平稳MAB适配收益随时间变化的场景（如运输路线的收益因路况、季节变化而波动）。

算法思路

• 衰减历史数据权重（如指数移动平均：\(\hat{\mu}_i(t) = \gamma \hat{\mu}_i(t-1) + (1-\gamma) r_t\)，\(\gamma \in (0,1)\)，近期数据权重更高）；
• 滑动窗口（仅使用最近W轮的数据计算平均收益）；
• 自适应探索（收益波动大时，增加探索概率）。

五、在运输路线规划项目中的应用

多臂老虎机算法可用于以下核心模块：

5.1 应用场景1：动态路线选择（已知路线集优化）

• 问题：已提取K条候选运输路线，每条路线的收益（运输时间、成本、准时率）随路况波动，需动态选择最优路线。
• 算法选型：优先用汤普森采样 或UCB1 （无需调参，智能探索），若路线收益波动大，用非平稳TS/UCB（衰减历史数据）。
• 收益定义：将多目标转化为单目标收益，例如：\(r = w_1 \cdot (1 - \frac{实际时间-最短时间}{最短时间}) + w_2 \cdot (1 - \frac{实际成本-最低成本}{最低成本}) + w_3 \cdot 准时率\)（\(w_1,w_2,w_3\)为权重，可通过业务需求调整）。

5.2 应用场景2：新路线探索（未知路线发现）

• 问题：路线可能不是最优，需探索新的潜在路线（如绕开拥堵路段的备选路线）。
• 算法选型：ε-贪心（衰减ε） 或上下文TS（结合路况上下文探索新路线）。
• 逻辑：将新路线视为"新臂"，初期以较高概率探索，若收益优于现有路线，则增加选择频率；否则减少探索。

5.3 应用场景3：货运方式与路线组合优化

• 问题：选择"路线+货运方式"组合（如"路线A+普通货车""路线B+冷链货车"），需同时优化路线和货运方式。
• 算法选型：上下文多臂老虎机（将"路线+货运方式"作为"臂"，上下文为货物类型、天气、时间段）。

六、Python代码实现（经典算法+运输路线模拟）

以下提供完整的Python代码，实现ε-贪心、UCB1、汤普森采样三种经典算法，并模拟3条公路路线选择场景。

6.1 代码结构

1. 模拟收益生成（模拟3条路线的收益分布，含随机波动）；
2. 实现三种经典算法；
3. 运行模拟并可视化累积收益和遗憾。

6.2 完整代码

python

运行

import numpy as np
import matplotlib.pyplot as plt

# -------------------------- 1. 模拟运输路线收益分布 --------------------------
class RouteRewardSimulator:
    """模拟3条路线的收益（准时率，0-1之间，越高越好）"""
    def __init__(self):
        # 每条路线的真实收益分布（非平稳，含随机波动）
        self.route_params = {
            0: {"mean": 0.85, "std": 0.05},  # 路线1：平均准时率85%，波动小（最优路线）
            1: {"mean": 0.75, "std": 0.10},  # 路线2：平均准时率75%，波动中等
            2: {"mean": 0.65, "std": 0.15}   # 路线3：平均准时率65%，波动大（最差路线）
        }
    
    def get_reward(self, route_id, t):
        """获取第t轮选择路线route_id的收益（加入时间波动，模拟路况变化）"""
        params = self.route_params[route_id]
        # 模拟早高峰波动（t∈[50,150]时，准时率下降10%）
        peak_penalty = 0.1 if 50 <= t <= 150 else 0
        # 生成收益（确保在0-1之间）
        reward = np.random.normal(params["mean"] - peak_penalty, params["std"])
        return max(0, min(1, reward))

# -------------------------- 2. 多臂老虎机算法实现 --------------------------
class EpsilonGreedy:
    def __init__(self, k, epsilon=0.1, decay_epsilon=True):
        self.k = k  # 臂数（路线数）
        self.epsilon = epsilon  # 初始探索概率
        self.decay_epsilon = decay_epsilon  # 是否衰减epsilon
        self.counts = np.zeros(k)  # 每条路线的选择次数
        self.values = np.zeros(k)  # 每条路线的平均收益
    
    def select_arm(self, t):
        """第t轮选择路线（t从1开始）"""
        # 衰减epsilon：epsilon(t) = epsilon / sqrt(t)
        if self.decay_epsilon:
            current_epsilon = self.epsilon / np.sqrt(t)
        else:
            current_epsilon = self.epsilon
        
        # 探索：随机选择
        if np.random.random() < current_epsilon:
            return np.random.choice(self.k)
        # 利用：选择平均收益最高的路线
        else:
            return np.argmax(self.values)
    
    def update(self, arm, reward):
        """更新路线arm的选择次数和平均收益"""
        self.counts[arm] += 1
        # 增量更新平均收益（避免重新计算所有历史数据）
        self.values[arm] = (self.values[arm] * (self.counts[arm] - 1) + reward) / self.counts[arm]

class UCB1:
    def __init__(self, k):
        self.k = k
        self.counts = np.zeros(k)  # 选择次数
        self.values = np.zeros(k)  # 平均收益
    
    def select_arm(self, t):
        """第t轮选择路线（t≥k+1，确保每条路线至少被选1次）"""
        # 初始化：前k轮每条路线各选1次
        if t <= self.k:
            return t - 1
        
        # 计算UCB值
        ucb_values = np.zeros(self.k)
        for arm in range(self.k):
            # UCB1公式：平均收益 + 根号(2*ln(t)/选择次数)
            confidence = np.sqrt(2 * np.log(t) / self.counts[arm])
            ucb_values[arm] = self.values[arm] + confidence
        
        return np.argmax(ucb_values)
    
    def update(self, arm, reward):
        """更新参数（与贪心算法一致）"""
        self.counts[arm] += 1
        self.values[arm] = (self.values[arm] * (self.counts[arm] - 1) + reward) / self.counts[arm]

class ThompsonSampling:
    def __init__(self, k):
        self.k = k
        # 伯努利分布的共轭先验：Beta(alpha, beta)，初始值(1,1)（均匀分布）
        self.alpha = np.ones(k)
        self.beta = np.ones(k)
    
    def select_arm(self, t):
        """采样每个路线的虚拟收益，选择最大者"""
        theta_samples = np.random.beta(self.alpha, self.beta)
        return np.argmax(theta_samples)
    
    def update(self, arm, reward):
        """更新Beta分布参数（伯努利收益：reward∈{0,1}，若为连续收益需调整分布）"""
        # 这里假设收益是连续的（准时率0-1），用"成功次数=reward*100，失败次数=(1-reward)*100"近似
        success = int(reward * 100)
        failure = int((1 - reward) * 100)
        self.alpha[arm] += success
        self.beta[arm] += failure

# -------------------------- 3. 运行模拟 --------------------------
def run_simulation(algorithm, simulator, T=1000):
    """运行T轮模拟，返回累积收益和累积遗憾"""
    cumulative_reward = np.zeros(T)
    cumulative_regret = np.zeros(T)
    true_best_mean = max([simulator.route_params[i]["mean"] for i in range(3)])  # 真实最优收益
    
    for t in range(T):
        # 选择路线（t从0开始，算法中t从1开始）
        arm = algorithm.select_arm(t + 1)
        # 获取收益
        reward = simulator.get_reward(arm, t)
        # 更新算法参数
        algorithm.update(arm, reward)
        
        # 计算累积收益和遗憾
        cumulative_reward[t] = cumulative_reward[t-1] + reward if t > 0 else reward
        regret_t = true_best_mean - simulator.route_params[arm]["mean"]  # 本轮遗憾
        cumulative_regret[t] = cumulative_regret[t-1] + regret_t if t > 0 else regret_t
    
    return cumulative_reward, cumulative_regret

# -------------------------- 4. 可视化结果 --------------------------
if __name__ == "__main__":
    # 初始化模拟和算法
    simulator = RouteRewardSimulator()
    T = 1000  # 模拟轮次（对应1000次运输决策）
    algorithms = {
        "ε-Greedy(ε=0.1, 衰减)": EpsilonGreedy(k=3, epsilon=0.1, decay_epsilon=True),
        "UCB1": UCB1(k=3),
        "Thompson Sampling": ThompsonSampling(k=3)
    }
    
    # 运行所有算法
    results = {}
    for name, algo in algorithms.items():
        reward, regret = run_simulation(algo, simulator, T)
        results[name] = {"reward": reward, "regret": regret}
    
    # 绘制累积收益图
    plt.figure(figsize=(12, 5))
    plt.subplot(1, 2, 1)
    for name, data in results.items():
        plt.plot(data["reward"], label=name)
    plt.xlabel("运输次数（轮次）")
    plt.ylabel("累积收益（总准时率）")
    plt.title("不同算法的累积收益对比")
    plt.legend()
    plt.grid(True, alpha=0.3)
    
    # 绘制累积遗憾图
    plt.subplot(1, 2, 2)
    for name, data in results.items():
        plt.plot(data["regret"], label=name)
    plt.xlabel("运输次数（轮次）")
    plt.ylabel("累积遗憾")
    plt.title("不同算法的累积遗憾对比")
    plt.legend()
    plt.grid(True, alpha=0.3)
    
    plt.tight_layout()
    plt.show()

6.3 代码说明

1. 收益模拟：模拟3条路线的准时率收益，加入早高峰波动（第50-150轮准时率下降10%），贴近真实运输场景；
2. 算法实现 ：
   • ε-贪心：支持衰减探索概率，适合初期多探索；
   • UCB1：无需调参，基于置信区间智能探索；
   • 汤普森采样：用Beta分布建模收益，适合连续型收益（准时率0-1）；
3. 可视化：对比三种算法的累积收益和遗憾，可直观看出汤普森采样和UCB1的长期性能更优。

6.4 运行结果分析

• 累积收益：汤普森采样和UCB1最终收益更高，因它们能更智能地探索最优路线，且适应收益波动；
• 累积遗憾：汤普森采样的遗憾增长最慢，因它基于概率信念探索，避免盲目尝试差路线；
• 实际应用：可根据项目需求调整收益函数（如加入成本、时间权重），或扩展为上下文多臂老虎机（加入路况、天气等上下文）。

七、算法选择建议

算法	优点	缺点	适用场景
纯贪心	实现最简单，计算快	无探索，长期遗憾高	收益固定、初始数据充足的简单场景
ε-贪心（衰减）	实现简单，探索可控	盲目标探索，需调参	快速验证、对性能要求不高的场景
UCB1	智能探索，无需调参，遗憾最优	初期探索较多，短期收益略低	收益分布稳定、需要自动平衡探索利用的场景
汤普森采样	概率探索，支持上下文，适应波动	需假设收益分布	收益波动、多上下文、多目标的复杂场景（推荐）

八、总结

多臂老虎机算法的核心是"探索-利用权衡"，通过动态决策最大化长期收益。在你的运输路线规划项目中：

1. 优先选择汤普森采样 或上下文多臂老虎机，适配路线收益波动、多上下文（路况、天气）的场景；
2. 收益函数需结合业务目标（时间、成本、准时率）设计，量化多目标为单目标或使用多目标MAB；
3. 若路线收益随时间变化（如季节、政策影响），需使用非平稳MAB（衰减历史数据权重）。