Cyber骇客的LIFO深渊与FIFO管道 ——【初阶数据结构与算法】栈与队列

量子炒饭大师2025-12-21 9:02

🎥个人简介
🌊🌉🌊心手合一，水到渠成


点击下面查看作者专栏 🏞️🏞️作者主页🏞️🏞️ 🔥🔥C语言专栏🔥🔥 🌊🌊编程百度🌊🌊 🌠🌠如何获取自己的代码仓库🌠🌠

索引与导读

💻栈

🧐概念与结构

栈是一种特殊的线性表数据结构，其只允许其在固定的一段进行插入和删除元素操作

  • 进行数据的插入与删除的操作的一端称为栈顶
  • 另一端称为栈底

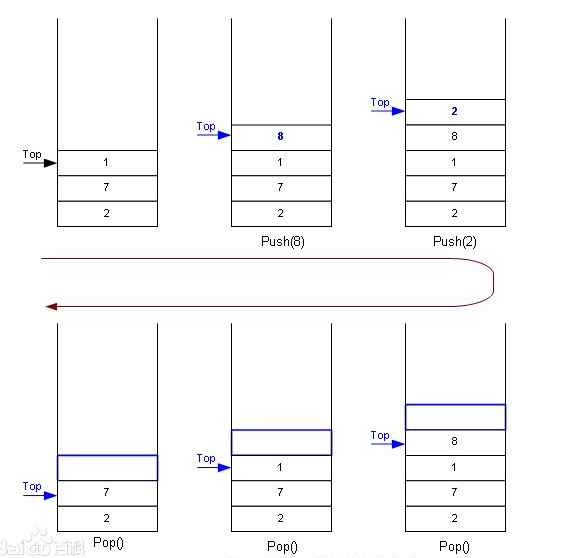
栈中的数据元素遵循先出后进LIFO的原则

🌠压栈

栈的插入操作叫做进栈/压栈/入栈

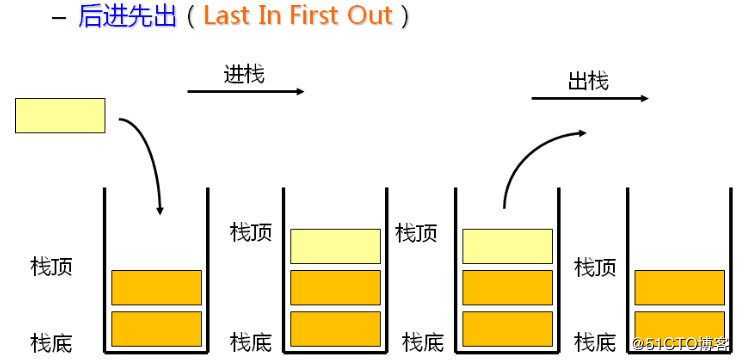
🌠出栈

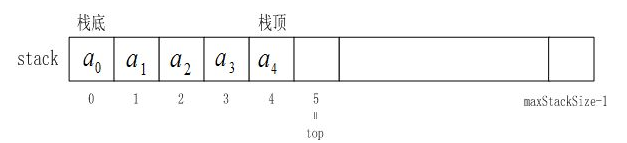
🧐利用数组实现栈

栈的实现一般可以使用数组或者链表 实现，相对而言数组的结构实现更优一些
因为数组在尾上插入数据的代价比较小，时间和空间复杂度都是O(1)

❗数组可以用来实现栈 ，但这并不意味着栈的本质就是数组 。数组是一种连续存储元素的数据结构，使用数组实现栈时，利用数组的索引来模拟栈的操作

📍我们本质上只需要关注栈顶 就行了，栈底不需要关心

📁分文件编写

text 复制代码 
Stack
├── Stack.h      // 栈的头文件
├── Stack.c      // 栈的实现文件
└── test.c       // 测试主程序
❗主要结构体
c 复制代码 
struct Stack {
	int* arr;
	int top;
	int capacity;
}

🔥🔥🔥🔥讲解代码要点：
arr指向动态开辟的数组
top指向栈顶指针，指向栈顶元素的下一个位置，也代表元素个数
capacity栈的容量

🔎Stack.h
c 复制代码 
#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <assert.h>

// 定义栈的数据类型，方便后续更改（如改为 char 或 double）
typedef int STDataType;

// 栈的结构定义
typedef struct Stack {
    STDataType* arr;    // 指向动态开辟的数组
    int top;            // 栈顶指针（指向栈顶元素的下一个位置，也代表元素个数）
    int capacity;       // 栈的容量
} ST;

// 栈的初始化
void STInit(ST* ps);

// 栈的销毁
void STDestroy(ST* ps);

// 入栈（栈顶插入）
void STPush(ST* ps, STDataType x);

// 出栈（栈顶删除）
void STPop(ST* ps);

// 判断栈是否为空
bool STEmpty(ST* ps);

// 获取栈顶元素
STDataType STTop(ST* ps);

// 获取栈中有效数据个数
int STSize(ST* ps);
🔎Stack.c
1）栈的初始化
c 复制代码 
void STInit(ST* ps) {
	assert(ps);

	ps->arr = NULL;
	ps->top = ps->capacity = 0;
}

🔥🔥🔥🔥ps指针不能为空

2）栈的销毁
c 复制代码 
void STDestroy(ST* ps) {
	assert(ps);

	if (ps->arr) {
		free(ps->arr);
	}

	ps->arr = NULL;
	ps->top = ps->capacity = 0;
}

🔥🔥🔥🔥讲解代码要点：
指针要释放后置空

3）入栈------栈顶
c 复制代码 
void STPush(ST* ps, STDataType x) {
	assert(ps);			//ps指针不能为空

	//判断空间是否足够
	if (ps->top == ps->capacity) {
		//空间不够，扩容
		int newCapacity = ((ps->capacity == 0) ? 4 : ps->capacity * 2);
		STDataType* temp = (STDataType*)realloc(ps->arr, newCapacity * sizeof(STDataType));
		if (temp == NULL) {
			perror("realloc fail!!!");
			exit(-1);
		}
		ps->arr = temp;
		ps->capacity = newCapacity;
	}
//空间足够，直接入栈
	ps->arr[ps->top++] = x;
}

🚩需要注意的是： 这里的realloc使用机制
newCapacity * sizeof(STDataType)表示总个数

👉例如 newCapacity初始表示4个而不是4个整型

🔗Lucy的空间骇客裂缝：动态内存管理（realloc）

4）出栈------栈顶
c 复制代码 
void STPop(ST* ps) {
	assert(!STEmpty(ps));			//栈不能为空，否则没有数据可出

	(ps->top)--;
}

🚩注意栈不能为空，否则没有数据可以取出

🚩这里有个疑惑------------为什么(ps->top)--不用对每个索引的内存进行释放？

答案请看如下：

💥内存管理方式：连续空间 vs 独立节点
  • 首先我们先明白我们本次是利用顺序表实现的数组栈
  • 顺序表代表的是连续空间 ，顺序栈通常通过 malloc 一次性申请一块连续的内存空间
  • 出栈时，我们只是逻辑上减少了栈顶指针（或下标） ，原本存储的数据依然留在内存块中，只是不再被视为有效数据（也就是依然有指针指向它）
  • 如果是链表实现的栈，出栈时必须 free 掉节点内存 ，因为每个节点是独立申请的堆内存，不释放会导致内存泄漏

ps->top--出栈操作本质上是逻辑删除,它告诉程序 "当前有效数据的边界缩小了"

  • 覆盖机制： 当你下一次执行 STPush（入栈）时，新的数据会直接覆盖掉原来出栈位置留下的"垃圾数据"。
    因此，没有必要专门花时间去清理或释放那一小块内存
  • 内存释放： 由于整块内存是一个整体，你不能只"释放"数组中的某一个格子。只有在销毁整个顺序表时，才会调用 free 释放掉整块空间。

链表：

  • 物理结构： 它的每一个节点都是独立申请的。每个节点在内存中可能散落在各个角落，通过指针相互连接。
  • 删除逻辑： 删除一个节点时，必须执行物理删除。因为该节点是独立申请的堆内存，如果不手动释放，这块内存就永远无法被系统回收，从而导致内存泄漏。
  • 内存释放： 每删除一个节点，就需要立即调用 free 释放该节点的内存。
5）判断栈是否为空
c 复制代码 
bool STEmpty(ST* ps) {
	assert(ps);
	return ps->top == 0;
}

🚩使用bool记得添加头文件stdbool.h

当然也可以不使用bool定义👇

c 复制代码 
int STEmpty(ST* ps)
{
	assert(ps);
	return ps->top == 0 ? 0 : 1;
}

🚩如果栈为空，就返回0，条件不会执行；如果不为空，就返回1，条件为真继续执行

6）获取栈顶元素
c 复制代码 
STDataType STTop(ST* ps) {
	assert(!STEmpty(ps));			//栈不能为空，否则没有数据可取

	return ps->arr[ps->top - 1];
}

🚩top - 1表示最后一个元素，即栈顶

7）获取栈中的有效数据个数
c 复制代码 
int STSize(ST* ps) {		//STDataType是栈中的数据类型，int是明确的数据类型
	assert(ps);
	
	return ps->top;
}

🚩int与STDataType的区别❗

  • int是明确的数据类型
  • STDataType是栈中的数据类型
  • 我们返回栈中的有效数据个数，而不是返回栈的数据，所以返回int
完整代码
c 复制代码 
#include "Stack.h"

/*栈的初始化*/
void STInit(ST* ps) {
	assert(ps);

	ps->arr = NULL;
	ps->top = ps->capacity = 0;
}

/*栈的销毁*/
void STDestroy(ST* ps) {
	assert(ps);

	if (ps->arr) {
		free(ps->arr);
	}

	ps->arr = NULL;
	ps->top = ps->capacity = 0;
}

/*入栈------栈顶*/
void STPush(ST* ps, STDataType x) {
	assert(ps);			//ps指针不能为空

	//判断空间是否足够
	if (ps->top == ps->capacity) {
		//空间不够，扩容
		int newCapacity = ((ps->capacity == 0) ? 4 : ps->capacity * 2);
		STDataType* temp = (STDataType*)realloc(ps->arr, newCapacity * sizeof(STDataType));
		if (temp == NULL) {
			perror("realloc fail!!!");
			exit(-1);
		}
		ps->arr = temp;
		ps->capacity = newCapacity;
	}
//空间足够，直接入栈
	ps->arr[ps->top++] = x;
}

/*出栈------栈顶*/
void STPop(ST* ps) {
	assert(!STEmpty(ps));			//栈不能为空，否则没有数据可出

	(ps->top)--;
}

//判断栈是否为空
bool STEmpty(ST* ps) {
	assert(ps);
	return ps->top == 0;
}

//获取栈顶元素
STDataType STTop(ST* ps) {
	assert(!STEmpty(ps));			//栈不能为空，否则没有数据可取

	return ps->arr[ps->top - 1];
}

//获取栈中的有效数据个数
int STSize(ST* ps) {		//STDataType是栈中的数据类型，int是明确的数据类型
	assert(ps);
	
	return ps->top;
}
🔎test.c
c 复制代码 
#include "Stack.h"

void TeskStack() {
	ST st;
	STInit(&st);

	// 1. 入栈测试
	STPush(&st, 1);
	STPush(&st, 2);
	STPush(&st, 3);
	STPush(&st, 4);

	printf("栈的大小：%d\n", STSize(&st));
	printf("当前栈顶的元素：%d\n", STTop(&st));

	// 2. 遍历测试 (栈的特性是后进先出 LIFO)
	printf("开始出栈打印: ");
	while (!STEmpty(&st)) {
		printf("%d ", STTop(&st));
		STPop(&st);
	}
	printf("\n");

	// 3. 销毁测试
	STDestroy(&st);
	printf("栈已销毁。\n");
}

int main() {
	TeskStack();
	return 0;
}

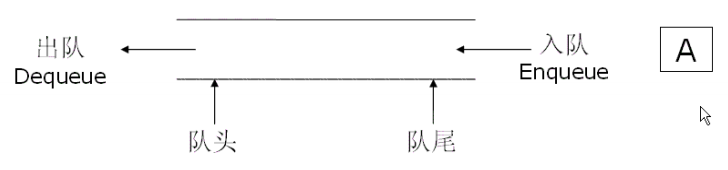
💻队列

队列是一种 先进先出（First In, First Out，简称 FIFO） 的线性数据结构。

  • 核心特点：

    • 操作受限：只允许在一端（队尾/Rear） 进行插入（入队/Enqueue） 操作，在另一端（队头/Front） 进行删除（出队/Dequeue） 操作。

    • FIFO 原则：最先进入队列的元素，将最先被移出队列。就像现实生活中的排队一样，先来的人先接受服务。

  • 主要术语：

    • 入队：向队尾添加一个新元素。

    • 出队：从队头移除一个元素。

    • 队头：允许进行删除操作的一端，存放的是最先进入、等待被处理的元素。

    • 队尾：允许进行插入操作的一端，存放的是最新进入的元素。

    • 空队列：队列中没有任何元素。

  • 图解队列

🧐队列的实现

队列也可以数组和链表的结构实现，使用链表的结构实现更优一些

因为如果使用数组的结构，出队列在数组头上出数据，效率会比较低。

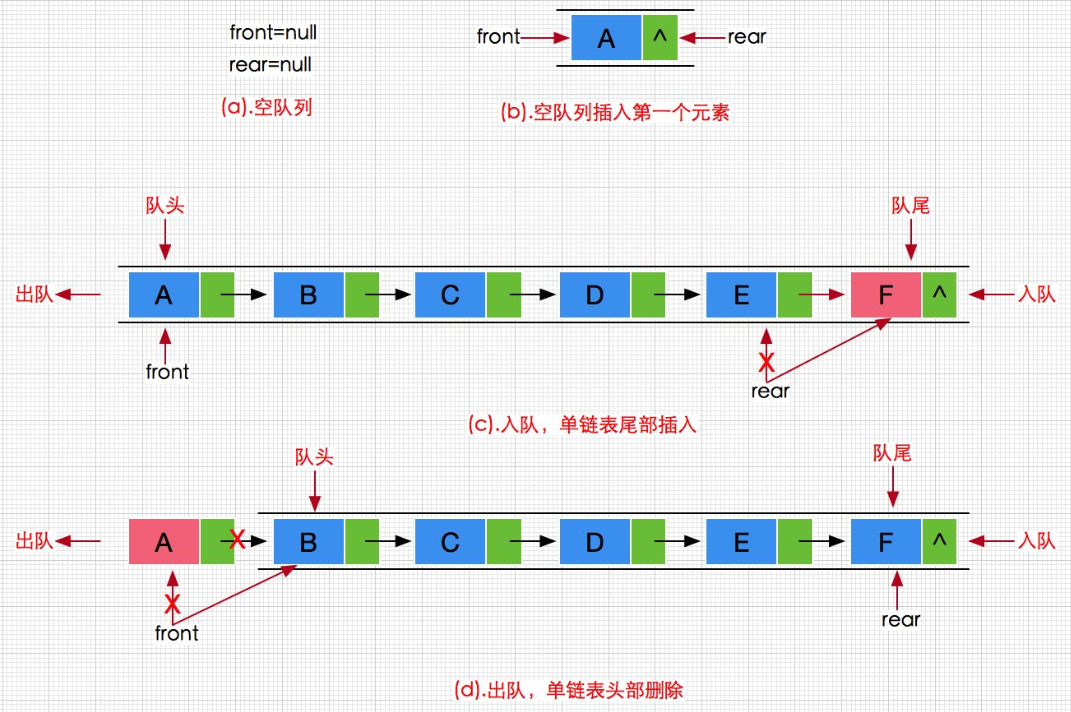
所以队列需要建立两个结构体

  • 一个用来存储链表节点
  • 一个用来存储表示队列，存储队头 和队尾

🔎关键结构体

c 复制代码 
struct QueueNode {
	int data;
	struct QueueNode* next;
}

🚩队列节点结构

c 复制代码 
struct Queue {
	QueueNode* phead;
	QueueNode* ptail;
	int size;
}

🚩队列控制结构

phead

  • 记录队头指针

ptail

  • 记录队尾指针

size

  • 记录有效元素个数

📁分文件编写

主项目目录 队列模块 包含 实现 test.c queue.h queue.c

🔎Queue.h

c 复制代码 
#ifndef QUEUE_H
#define QUEUE_H

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <stdbool.h>

// 定义队列数据类型
typedef int QDataType;

// 队列节点结构
typedef struct QueueNode {
    QDataType data;
    struct QueueNode* next;
} QueueNode;

// 队列控制结构
typedef struct Queue {
    QueueNode* phead; // 队头指针
    QueueNode* ptail; // 队尾指针
    int size;         // 记录有效元素个数
} Queue;

// 函数声明
void QueueInit(Queue* pg);
void QueuePush(Queue* pq, QDataType x);
void QueuePop(Queue* pq);
bool QueueEmpty(Queue* pq);
QDataType QueueFront(Queue* pq);
QDataType QueueBack(Queue* pq);
int QueueSize(Queue* pq);
void QueueDestroy(Queue* pq);

#endif

🔎Queue.c

1）队列初始化
c 复制代码 
//初始化
void QueueInit(Queue* pg) {
	assert(pg);
	pg->phead = pg->ptail = NULL;
	pg->size = 0;
}

🚩队列的头部指针 head 和尾部指针 tail 都设置为 NULL，表示队列为空，同时将队列的元素数量 size 初始化为 0

2）入队列
c 复制代码 
//入队列
void QueuePush(Queue* pq, QDataType x) {
	assert(pq);
	//创建值为x的节点
	QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));
	if (newnode == NULL) {
		perror("malloc fail!!!");
		exit(-1);
	}
	newnode->data = x;
	newnode->next = NULL;

	//队列为空
	if (pq->phead == NULL) {
		pq->phead = pq->ptail = newnode;
	}
	else {
		pq->ptail->next = newnode;
		pq->ptail = pq->ptail->next;
	}
	pq->size++;
}

🚩注意：

  • 队列的插入只能从尾部插入
  • 要先链接，后移动尾指针 ，否则找不到链接的节点 next 指针

如果队列为空

  • pq->phead = pq->ptail = newnode;让队列的phead与ptail都指向新节点

如果队列不为空

  • pq->ptail->next = newnode;让队列的尾节点指向新节点
  • pq->ptail = pq->ptail->next;再让队列尾节点移到新节点
3）判断队列是否为空
c 复制代码 
bool QueueEmpty(Queue* pq) {
	assert(pq);
	return pq->phead == NULL;	//C 语言的比较操作符是从左往右结合的
}

🚩易错点
return pq->phead == NULL;不能写成 return pq->phead == pq->ptail == NULL

相等运算符 == 的结合性是从左往右的

  • 第一步： 先计算左边的 pq->phead == pq->ptail
  • 第二步： 这个比较操作会返回一个布尔结果
  • 第三步： 用这个结果（0 或 1）再去和右边的NULL进行比较
  • 推荐写法：return pq->phead == NULL && pq->ptail == NULL;
4）出队列
c 复制代码 
void QueuePop(Queue* pq) {
	assert(!QueueEmpty(pq));
	//队列中只有一个节点
	if (pq->phead->next == NULL) {		//单节点判断
		free(pq->phead);
		pq->phead = pq->ptail == NULL;
	}
	else {
		QueueNode* next = pq->phead->next;
			free(pq->phead);
			pq->phead = next;
	}
	pq->size--;			//维护有效个数
}

🚩注意：

  • 出队列只能从头出
  • 先释放再置空
5）取队头数据
c 复制代码 
QDataType QueueFront(Queue* pq) {
	assert(!QueueEmpty(pq));
	return pq->phead->data;
}
6）取队尾数据
c 复制代码 
QDataType QueueBack(Queue* pq) {
	assert(!QueueEmpty(pq));
	return pq->ptail->data;
}
7）队列有效元素个数
c 复制代码 
int QueueSize(Queue* pq) {
	assert(pq);
	/*QueueNode* pcur = pq->phead;
	int size = 0;
	while (pcur) {
		pcur = pcur->next;
		++size;
	}
	return size;*/
	return pq->size;
}
8）队列的销毁
c 复制代码 
void QueueDestroy(Queue* pq) {
	assert(pq);

	QueueNode* pcur = pq->phead;
	while (pcur) {
		QueueNode* next = pcur->next;
		free(pcur);
		pcur = next;
	}
	pq->phead = pq->ptail = NULL;
	pq->size = 0;
}

🔎test.c

c 复制代码 
#include "Queue.h"

void TestQueue() {
	Queue q;
	QueueInit(&q);

    // 入队测试
    QueuePush(&q, 1);
    QueuePush(&q, 2);
    QueuePush(&q, 3);
    QueuePush(&q, 4);

    printf("队列大小: %d\n", QueueSize(&q));
    printf("队头元素: %d\n", QueueFront(&q));
    printf("队尾元素: %d\n", QueueBack(&q));

    // 出队并打印测试
    printf("出队顺序: ");
    while (!QueueEmpty(&q)) {
        printf("%d ", QueueFront(&q));
        QueuePop(&q);
    }
    printf("\n");

    QueueDestroy(&q);
    printf("队列已销毁\n");
}

int main() {
	TestQueue();
	return 0;
}

🔄循环队列

循环队列是一种为了解决普通顺序队列假溢出问题而设计的线性数据结构

它将数组的头尾相连，在逻辑上形成一个环状空间

❓何为"假溢出"？

在普通数组队列中，当队列中的数据从队头移出后，队尾重新插入数据时候，会导致队尾的指针超出数组大小范围，系统会提示队列已满

这就是我们所说的假溢出

图示讲解

  • 初始队列
Plaintext 复制代码 
下标： [ 0 ] [ 1 ] [ 2 ] [ 3 ] [ 4 ]
数据：  (A)   (B)    C     D    (空)
                    ↑     ↑
                  front  rear
  • 继续入队E
Plaintext 复制代码 
下标： [ 0 ] [ 1 ] [ 2 ] [ 3 ] [ 4 ]
数据：  (A)   (B)    C     D     E
                    ↑           ↑
                  front        rear(到头了)
  • 你想再入队F

看空间： 下标0和1是空的，完全可以放

看指针： rear 已经指向了下标 4（数组的物理尽头）。在普通数组逻辑里，rear + 1 就越界了。

结果： 指针"撞墙"，无法再移动，队列宣告"已满"

🤔本质
  • 普通数组队列
    在普通数组队列中，我们如果要实现元素前移，所需要的时间复杂度是O(n)，实际开发中不会被运用
    在如果我们实现指针前移，实际上数据还是停留在原来的位置没有移动
    在逻辑上可以"模拟"前移，但在物理存储上，元素依然在原地
  • 循环队列
    数据不动，只把记录"队头在哪"的那个数字（front）加 1，复杂度永远是O(1)

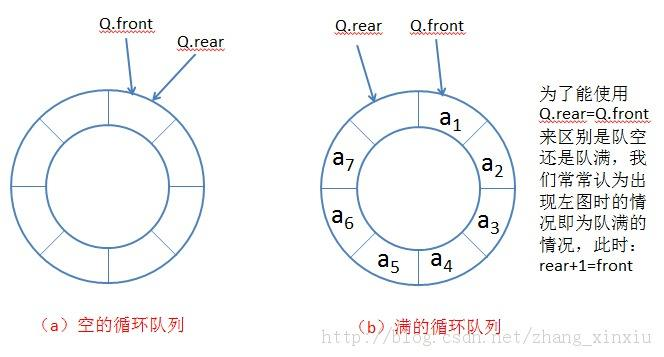
循环队列实现的核心逻辑公式

在实现之前，我们需要明确几个关键的计算逻辑（假设数组长度为 N N N）：索引更新（环绕）： 无论是入队还是出队，指针移动都需要取模： i n d e x = ( i n d e x + 1 ) ( m o d N ) index = (index + 1) \pmod N index=(index+1)(modN)判空条件： f r o n t = = r e a r front == rear front==rear判满条件： 为了区分空和满，我们通常会预留一个空位不存数据，或者维护一个 size 变量。最经典的"预留空位法"判满公式为： ( r e a r + 1 ) ( m o d N ) = = f r o n t (rear + 1) \pmod N == front (rear+1)(modN)==front

完整代码

c 复制代码 
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

// 定义循环队列结构体
typedef struct {
    int *data;      // 动态数组指针
    int front;      // 队头指针
    int rear;       // 队尾指针
    int capacity;   // 数组实际容量 (k + 1)
} MyCircularQueue;

/**
 * 初始化队列
 * k: 队列想要存储的有效元素个数
 */
MyCircularQueue* myCircularQueueCreate(int k) {
    MyCircularQueue* obj = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    // 实际申请空间为 k + 1，用于区分空和满
    obj->capacity = k + 1;
    obj->data = (int*)malloc(sizeof(int) * obj->capacity);
    obj->front = 0;
    obj->rear = 0;
    return obj;
}

/**
 * 检查队列是否为空
 */
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    return obj->front == obj->rear;
}

/**
 * 检查队列是否已满
 */
bool myCircularQueueIsFull(MyCircularQueue* obj) {
    return (obj->rear + 1) % obj->capacity == obj->front;
}

/**
 * 入队
 */
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    if (myCircularQueueIsFull(obj)) {
        return false;
    }
    
    obj->data[obj->rear] = value;
    // 移动 rear 指针，并取模实现循环
    obj->rear = (obj->rear + 1) % obj->capacity;
    return true;
}

/**
 * 出队
 */
bool myCircularQueueDeQueue(MyCircularQueue* obj) {
    if (myCircularQueueIsEmpty(obj)) {
        return false;
    }
    
    // 移动 front 指针，逻辑上删除元素
    obj->front = (obj->front + 1) % obj->capacity;
    return true;
}

/**
 * 获取队头元素
 */
int myCircularQueueFront(MyCircularQueue* obj) {
    if (myCircularQueueIsEmpty(obj)) {
        return -1;
    }
    return obj->data[obj->front];
}

/**
 * 获取队尾元素
 */
int myCircularQueueRear(MyCircularQueue* obj) {
    if (myCircularQueueIsEmpty(obj)) {
        return -1;
    }
    // rear 指向的是下一个空位，所以前一个位置才是队尾
    // 加上 capacity 再取模是为了防止 (rear - 1) 变成负数
    int index = (obj->rear - 1 + obj->capacity) % obj->capacity;
    return obj->data[index];
}

/**
 * 释放内存
 */
void myCircularQueueFree(MyCircularQueue* obj) {
    if (obj != NULL) {
        if (obj->data != NULL) {
            free(obj->data);
        }
        free(obj);
    }
}

// --- 测试主函数 ---
int main() {
    // 创建容量为 3 的循环队列
    MyCircularQueue* obj = myCircularQueueCreate(3);

    printf("入队 1: %d\n", myCircularQueueEnQueue(obj, 1)); // 1 (true)
    printf("入队 2: %d\n", myCircularQueueEnQueue(obj, 2)); // 1 (true)
    printf("入队 3: %d\n", myCircularQueueEnQueue(obj, 3)); // 1 (true)
    printf("入队 4 (满): %d\n", myCircularQueueEnQueue(obj, 4)); // 0 (false)

    printf("队尾元素: %d\n", myCircularQueueRear(obj));  // 3
    printf("队满?: %d\n", myCircularQueueIsFull(obj));   // 1 (true)

    printf("出队: %d\n", myCircularQueueDeQueue(obj));   // 1 (true)
    printf("入队 4: %d\n", myCircularQueueEnQueue(obj, 4)); // 1 (true)
    printf("队尾元素: %d\n", myCircularQueueRear(obj));  // 4

    // 别忘了释放内存
    myCircularQueueFree(obj);

    return 0;
}

栈与队列的概念题与面试题

面试题

🔗Lucy的空间骇客裂缝：有效括号
🔗Lucy的空间骇客裂缝：用队列实现栈
🔗Lucy的空间骇客裂缝：用栈实现队列
🔗Lucy的空间骇客裂缝：设计循环队列

概念习题

1. 栈的出栈顺序

题目描述：

一个栈的初始状态为空。现将元素 1、2、3、4、5、A、B、C、D、E 依次入栈 ，然后再依次出栈，则元素出栈的顺序是（ ）。

A. 12345ABCDE

B. EDCBA54321

C. ABCDE12345

D. 54321EDCBA

正确答案：B

解析：

  • 考点：栈的"先进后出"（LIFO）特性。
  • 分析 ：题目明确说明操作顺序是 "全部入栈" 后 "再依次出栈"，中间没有穿插出栈操作。
  • 过程 ：
    • 入栈顺序：1 → 2 → 3 → 4 → 5 → A → B → C → D → E（此时 E 在栈顶）。
    • 出栈顺序：必然是入栈顺序的逆序。
    • 结果：E → D → C → B → A → 5 → 4 → 3 → 2 → 1。

2. 合法的出栈序列判断

题目描述：

若进栈序列为 1, 2, 3, 4，进栈过程中可以出栈，则下列 不可能 的一个出栈序列是（ ）。

A. 1, 4, 3, 2

B. 2, 3, 4, 1

C. 3, 1, 4, 2

D. 3, 4, 2, 1

正确答案：C

解析：

  • 考点：栈的操作合法性模拟。
  • 分析 ：
    • A (1,4,3,2) : 1进1出 -> 2,3,4进 -> 4出 -> 3出 -> 2出。(可行)
    • B (2,3,4,1) : 1进2进 -> 2出 -> 3进3出 -> 4进4出 -> 1出。(可行)
    • C (3,1,4,2) : 要先输出 3，意味着 1 和 2 必须先依次入栈且未出栈。此时栈内状态为 [底部:1, 顶部:2]。3 入栈并出栈后，下一个弹出的必须是栈顶的 2 ，绝对不可能是 1（因为 1 被 2 压在下面）。(不可行)
    • D (3,4,2,1) : 1,2,3进 -> 3出 -> 4进4出 -> 2出 -> 1出。(可行)

3. 循环队列的状态判断

题目描述：

循环队列的存储空间为 Q ( 1 : 100 ) Q(1:100) Q(1:100)，初始状态为 f r o n t = r e a r = 100 front=rear=100 front=rear=100。经过一系列正常的入队与退队操作后， f r o n t = r e a r = 99 front=rear=99 front=rear=99，则循环队列中的元素个数为（ ）。

A. 1

B. 2

C. 99

D. 0 或者 100

正确答案：D

解析：

  • 考点：循环队列的判空与判满条件。
  • 分析 ：
    • 在标准的循环队列中，当 front == rear 时，存在两种物理状态：
      1. 队列为空：所有元素已出队。
      2. 队列已满：元素填满了所有空间，尾指针追上了头指针。
    • 虽然工程上常用"牺牲一个存储单元"或"增加标志位"来区分空和满，但题目本身只给出了 front == rear 这一状态，从逻辑严谨性角度来看，它既可能是空（0个元素），也可能是满（100个元素）。

4. 队列的基本运算

题目描述：

以下 ( ) 不是 队列的基本运算？

A. 从队尾插入一个新元素

B. 从队列中删除第 i 个元素

C. 判断一个队列是否为空

D. 读取队头元素的值

正确答案：B

解析：

  • 考点：队列的定义（FIFO）。
  • 分析 ：
    • 队列的操作受限于两端：只能在队尾插入 （入队），在队头删除（出队）。
    • 选项 B 描述的是"随机访问"或"随机删除"，这是**线性表（数组/链表）**的特性，而不是队列的特性。

5. 循环队列有效长度计算公式

题目描述：

现有一循环队列，其队头指针为 front，队尾指针为 rear；循环队列长度为 N。其队内有效长度为？(假设队头不存放数据)

A. (rear - front + N) % N + 1

B. (rear - front + N) % N

C. (rear - front) % (N + 1)

D. (rear - front + N) % (N - 1)

正确答案：B

解析：

  • 考点：循环队列元素个数通用公式。
  • 分析 ：
    • 我们需要处理 rear 绕回到数组开头（即 rear < front）的情况。
    • 通用公式推导 ：
      • 当 rear >= front 时，个数 = rear - front。
      • 当 rear < front 时，个数 = rear - front + N。
    • 为了将上述两种情况统一，使用取模运算：
      L e n g t h = ( r e a r − f r o n t + N ) % N Length = (rear - front + N) \% N Length=(rear−front+N)%N

总结：关键知识点 Cheat Sheet

  1. 栈 (Stack)：

    • 特性：先进后出 (LIFO)。
    • 合法序列技巧 ：如果出栈序列中某元素为 k k k，则在该元素之后出栈的所有比 k k k 小的元素，必须按递减顺序排列。

  2. 循环队列 (Circular Queue)：

    • 判空条件 ：front == rear
    • 判满条件 （常用牺牲一格法）：(rear + 1) % N == front
    • 队列长度公式 ：(rear - front + N) % N
    • 入队索引 ：rear = (rear + 1) % N
    • 出队索引 ：front = (front + 1) % N

💻结尾--- 核心连接协议

警告： 🌠🌠正在接入底层技术矩阵。如果你已成功破解学习中的逻辑断层，请执行以下指令序列以同步数据：🌠🌠

【📡】 建立深度链接： 关注本终端。在赛博丛林中深耕底层架构，从原始代码到进阶协议，同步见证每一次系统升级。

【⚡】 能量过载分发： 执行点赞操作。通过高带宽分发，让优质模组在信息流中高亮显示，赋予知识跨维度的传播力。

【💾】 离线缓存核心： 将本页加入收藏。把这些高频实战逻辑存入你的离线存储器，在遭遇系统崩溃或需要离线检索时，实现瞬时读取。

【💬】 协议加密解密： 在评论区留下你的散列码。分享你曾遭遇的代码冲突或系统漏洞（那些年踩过的坑），通过交互式编译共同绕过技术陷阱。

【🛰️】 信号频率投票： 通过投票发射你的选择。你的每一次点击都在重新定义矩阵的进化方向，决定下一个被全量拆解的技术节点。

相关推荐
Legendary_0083 小时前
Type-C一拖三快充线的核心优势与LDR6020方案深度解析
c语言·开发语言·电脑
青出于兰3 小时前
C语言| 指针变量的自增运算
c语言·开发语言
一起养小猫3 小时前
LeetCode100天Day3-判断子序列与汇总区间
java·数据结构·算法·leetcode
Joy-鬼魅3 小时前
vs调试器设置解决创建共享内存返回错误码5的问题
c++·microsoft·createfilemap·vc
404未精通的狗4 小时前
（数据结构）二叉树、二叉搜索树+简单的排序算法（考前速成版）
数据结构·算法·排序算法
太理摆烂哥4 小时前
数据结构之并查集
数据结构
Emilia486.4 小时前
C++ 类与对象：解锁面向对象编程的核心密码（中）
开发语言·c++
soft20015254 小时前
MySQL Buffer Pool性能优化：LRU链表极致设计之道
数据库·mysql·链表
开压路机4 小时前
模拟实现反向迭代器
前端·c++
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03Linux下V2Ray安装配置指南04BongoCat - 跨平台键盘猫动画工具05在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）06jdk21下载、安装（Windows、Linux、macOS）07安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）08sqli-labs靶场通关笔记：第18-19关 HTTP头部注入09Open-AutoGLM Windows 安装部署教程10RedissonClient的配置解析