（leetcode）力扣100 18矩阵置零（哈希）

题目

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。

数据范围

m == matrix.length n == matrix[0].length

1 <= m, n <= 200

-2³¹ <= matrix[i][j] <= 2³¹ - 1

测试用例

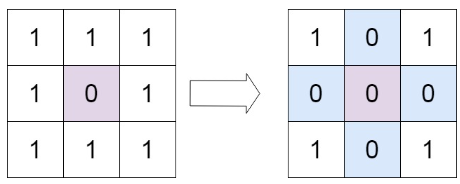
示例1

输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
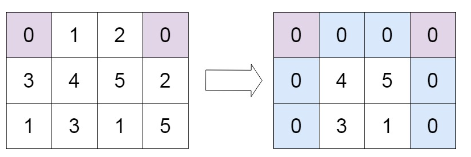
输出：[[1,0,1],[0,0,0],[1,0,1]]

示例2

输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]

题解1（普通哈希 空间复杂度O（n+m））

class Solution {
    public static void setZeroes(int[][] matrix) {
        int m=matrix.length;
        int n=matrix[0].length;
        boolean row[]=new boolean[m];
        boolean line[]=new boolean[n];

        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(matrix[i][j]==0){
                    row[i]=true;
                    line[j]=true;
                }
            }
        }

        for(int i=0;i<n;i++){
            if(line[i]){
                for(int j=0;j<m;j++){
                    matrix[j][i]=0;
                }
            }
        }

        for(int j=0;j<m;j++){
            if(row[j]){
                for(int i=0;i<n;i++){
                    matrix[j][i]=0;
                }
            }
        }


//
//        for(int a[]:matrix){
//            for(int b:a){
//                System.out.print(b+" ");
//            }
//            System.out.println();
//        }

    }
}

题解2(空间复杂度O（1）两个常量空间)

class Solution {
    public void setZeroes(int[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        boolean flagCol0 = false, flagRow0 = false;
        for (int i = 0; i < m; i++) {
            if (matrix[i][0] == 0) {
                flagCol0 = true;
            }
        }
        for (int j = 0; j < n; j++) {
            if (matrix[0][j] == 0) {
                flagRow0 = true;
            }
        }
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (matrix[i][j] == 0) {
                    matrix[i][0] = matrix[0][j] = 0;
                }
            }
        }
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (matrix[i][0] == 0 || matrix[0][j] == 0) {
                    matrix[i][j] = 0;
                }
            }
        }
        if (flagCol0) {
            for (int i = 0; i < m; i++) {
                matrix[i][0] = 0;
            }
        }
        if (flagRow0) {
            for (int j = 0; j < n; j++) {
                matrix[0][j] = 0;
            }
        }
    }
}

题解3（空间复杂度O（1），一个常量空间）

class Solution {
    public void setZeroes(int[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        boolean flagCol0 = false;
        for (int i = 0; i < m; i++) {
            if (matrix[i][0] == 0) {
                flagCol0 = true;
            }
            for (int j = 1; j < n; j++) {
                if (matrix[i][j] == 0) {
                    matrix[i][0] = matrix[0][j] = 0;
                }
            }
        }
        for (int i = m - 1; i >= 0; i--) {
            for (int j = 1; j < n; j++) {
                if (matrix[i][0] == 0 || matrix[0][j] == 0) {
                    matrix[i][j] = 0;
                }
            }
            if (flagCol0) {
                matrix[i][0] = 0;
            }
        }
    }
}

思路

关于这道题，题目一开始还把我唬住了，我挺好奇什么是原地算法。

简单来说，"原地算法"（In-place Algorithm）就是：不借用额外的空间，直接在给你的原始数据上进行修改。

一开始不懂原地算法，就按自己理解用哈希写了第一版代码，也就是博客中的代码1。当我去看题解时，发现题解1方法与此相同，那么我就有疑问了，既然都说原地算法了，为啥还要给出空间复杂度为O（M+N）的题解1呢，奇怪。

这道题的整体难度不高，如果理解了原地算法什么意思，我们就能清晰的了解到题目的要求，在原有数组上进行涂抹修改，完成算法。（单个变量空间的申请不计入）

方法二的思路就是用第一行第一列作为原本的哈希数组，只需要用两个单独变量作为记录第一行与第一列情况的变量即可。

方法三是观察到了，0,0这个位置在方法二中并没有被用到格子，被用来当一个记录变量，其他思路和方法二类似。

但是官方的第三个方法提到了倒序，博主个人认为是完全没有必要的，之所以采用倒序，是因为官方代码里直接就将需要做数据的第一行列入了被更新遍历循环里。导致只有从最后一行开始才能避免信息被提前改变。但我们只需要像方法二那样，第一行与第一列留到最后来修改，不放入到循环遍历里，就完全不需要绕一个弯想到倒序。 具体如下:

博主思路

// 1. 先处理 1 到 n-1 的内层 (正序)
for (int i = 1; i < m; i++) {
    for (int j = 1; j < n; j++) {
        if (matrix[i][0] == 0 || matrix[0][j] == 0) {
            matrix[i][j] = 0;
        }
    }
}
// 2. 最后单独处理第一行和第一列
if (flagCol0) { ... }
if (matrix[0][0] == 0) { ... } // 假设 matrix[0][0] 存的是第一行的命

源代码

for (int i = m - 1; i >= 0; i--) { // 重点在这里！
    for (int j = 1; j < n; j++) {
        if (matrix[i][0] == 0 || matrix[0][j] == 0) matrix[i][j] = 0;
    }
    if (flagCol0) matrix[i][0] = 0; // 他把第一列的更新写在了这里
}

这样做代码量就多了一两行，但思路上却简单了数倍。