



目录
- [P8727 [蓝桥杯 2020 国 A] 填空问题](#P8727 [蓝桥杯 2020 国 A] 填空问题)
- [试题 A :合数个数](#试题 A :合数个数)
- [试题 B :含 2 天数](#试题 B :含 2 天数)
- [试题 C :本质上升序列](#试题 C :本质上升序列)
- [试题 D:咫尺天涯](#试题 D:咫尺天涯)
- [试题 E:玩具蛇](#试题 E:玩具蛇)
- AC代码
P8727 [蓝桥杯 2020 国 A] 填空问题
题目描述
试题 A :合数个数
【问题描述】
一个数如果除了 1 1 1 和自己还有其他约数,则称为一个合数。例如: 1 , 2 , 3 1,2,3 1,2,3 不是合数,4,6 是合数。
请问从 1 1 1 到 2020 2020 2020 一共有多少个合数。
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
试题 B :含 2 2 2 天数
【问题描述】
小蓝特别喜欢 2 2 2 ,今年是公元 2020 2020 2020 年,他特别高兴,因为每天日历上都可以看到 2 2 2 。
如果日历中只显示年月日,请问从公元 1900 1900 1900 年 1 1 1 月 1 1 1 日到公元 9999 9999 9999 年 12 12 12 月 31 31 31 日,一共有多少天日历上包含 2 2 2 。即有多少天中年月日的数位中包含数字 2 2 2 。
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
试题 C :本质上升序列
【问题描述】
小蓝特别喜欢单调递增的事物。
在一个字符串中,如果取出若干个字符,将这些字符按照在字符串中的顺序排列后是单调递增的,则成为这个字符串中的一个单调递增子序列。
例如,在字符串 lanqiao 中,如果取出字符 n \mathrm{n} n 和 q \mathrm{q} q,则 n q \mathrm{nq} nq 组成一个单调递增子序列。类似的单调递增子序列还有 Inq、i、ano 等等。
小蓝发现,有些子序列虽然位置不同,但是字符序列是一样的,例如取第二个字符和最后一个字符可以取到 a o \mathrm{ao} ao,取最后两个字符也可以取到 ao。小蓝认为他们并没有本质不同。
对于一个字符串,小蓝想知道,本质不同的递增子序列有多少个?
例如,对于字符串 lanqiao,本质不同的递增子序列有 21 21 21 个。它们分别是 l、a、n、q、i、o、ln、an、lq、aq、nq、ai、lo、ao、no、io、lnq、 anq。
请问对于以下字符串(共 200 200 200 个小写英文字母,分四行显示):(如果你把以下文字复制到文本文件中,请务必检查复制的内容是否与文档中的一致。在试题目录下有一个文件 inc.txt,内容与下面的文本相同)
tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhf
iadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqij
gihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmad
vrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhewl本质不同的递增子序列有多少个?
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
试题 D:咫尺天涯
【问题描述】
皮亚诺曲线是一条平面内的曲线。
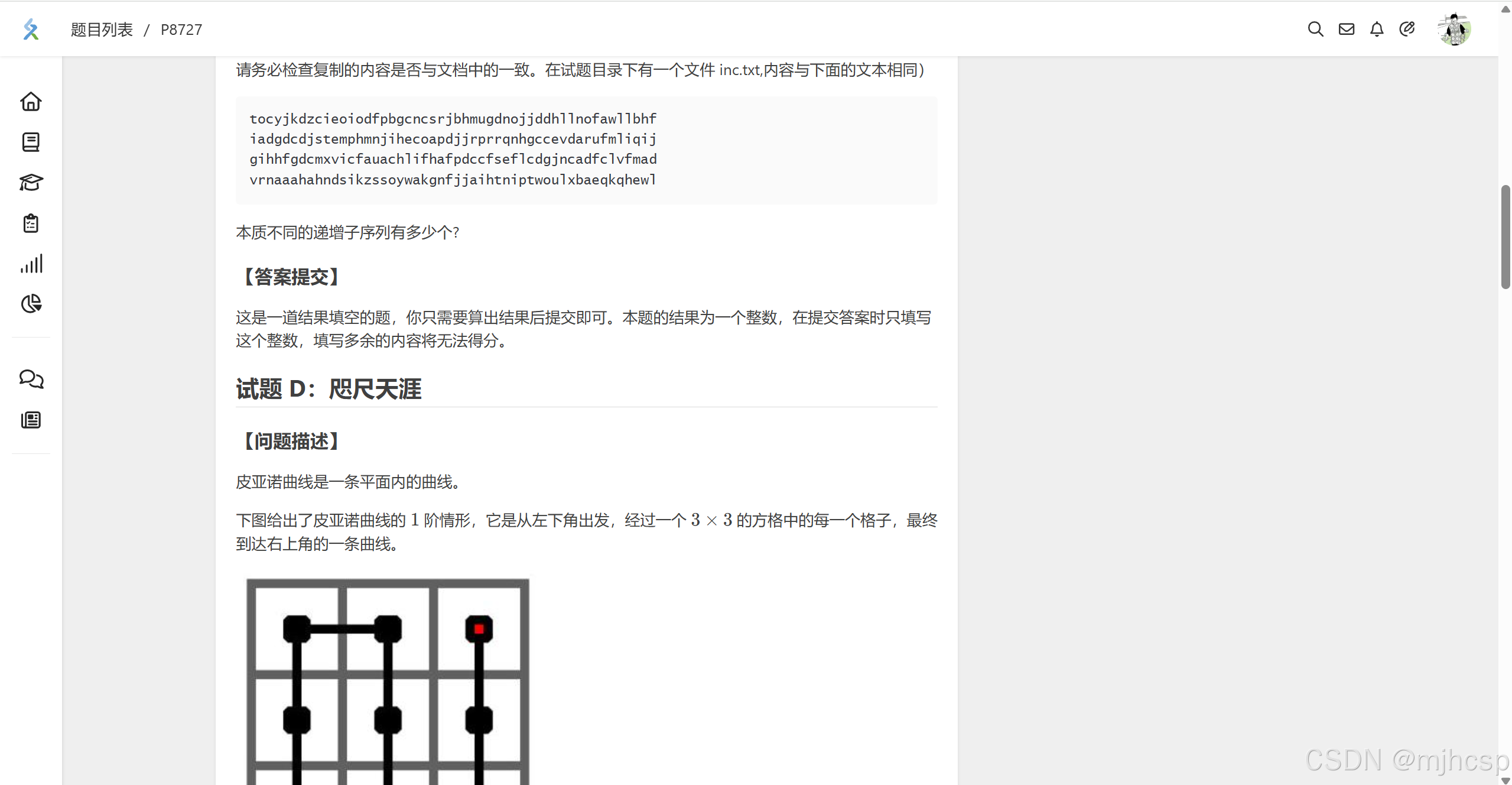
下图给出了皮亚诺曲线的 1 1 1 阶情形,它是从左下角出发,经过一个 3 × 3 3 \times 3 3×3 的方格中的每一个格子,最终到达右上角的一条曲线。
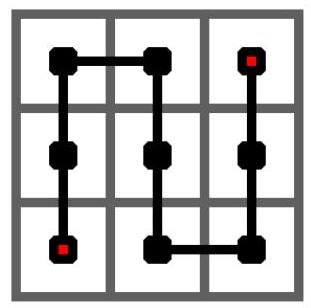
设每个格子的边长为 1 1 1 ,在上图中,有的相邻的方格(四相邻)在皮亚诺曲线中也是相邻的,在皮亚诺曲线上的距离是 1 1 1 ,有的相邻的方格在皮亚诺曲线中不相邻,距离大于 1 1 1 。
例如,正中间方格的上下两格都与它在皮亚诺曲线上相邻,距离为 1 1 1 ,左右两格都与它在皮亚诺曲线上不相邻,距离为 3 3 3 。
下图给出了皮亚诺曲线的 2 2 2 阶情形,它是经过一个 3 2 × 3 2 3^{2} \times 3^{2} 32×32 的方格中的每一个格子的一条曲线。它是将 1 1 1 阶曲线的每个方格由 1 1 1 阶曲线替换而成。
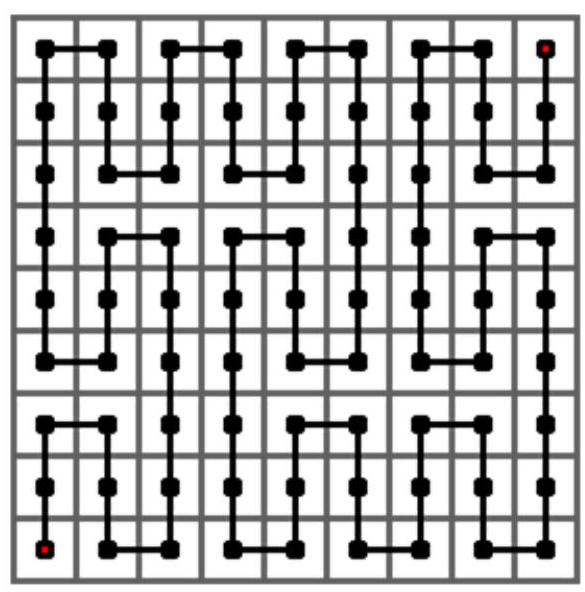
下图给出了皮亚诺曲线的 3 3 3 阶情形,它是经过一个 3 3 × 3 3 3^{3} \times 3^{3} 33×33 的方格中的每一个格子的一条曲线。它是将 2 2 2 阶曲线的每个方格由 1 1 1 阶曲线替换而成。

皮亚诺曲线总是从左下角开始出发,最终到达右上角。
小蓝对于相邻的方格在皮亚诺曲线上的相邻关系很好奇,他想知道相邻的方格在曲线上的距离之和是多少。
例如,对于 1 1 1 阶皮亚诺曲线,距离和是 24 24 24 ,有 8 8 8 对相邻的方格距离为 1 1 1 ,2 对相邻的方格距离为 3 3 3 ,2 对相邻的方格距离为 5 5 5 。
再如,对于 2 2 2 阶皮亚诺曲线,距离和是 816 816 816 。
请求出对于 12 12 12 阶皮亚诺曲线,距离和是多少。
提示:答案不超过 1 0 18 10^{18} 1018。
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
试题 E:玩具蛇
【问题描述】
小蓝有一条玩具蛇,一共有 16 16 16 节,上面标着数字 1 1 1 至 16 16 16 。每一节都是一个正方形的形状。相邻的两节可以成直线或者成 90 90 90 度角。
小蓝还有一个 4 × 4 4 \times 4 4×4 的方格盒子,用于存放玩具蛇,盒子的方格上依次标着字母 A \mathrm{A} A 到 P \mathrm{P} P 共 16 16 16 个字母。
小蓝可以折叠自己的玩具蛇放到盒子里面。他发现,有很多种方案可以将玩具蛇放进去。
下图给出了两种方案:
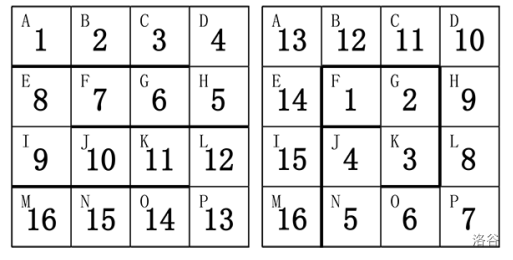
请帮小蓝计算一下,总共有多少种不同的方案。如果两个方案中,存在玩具蛇的某一节放在了盒子的不同格子里,则认为是不同的方案。
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
输入格式
输入一个大写字母,表示第几个问题。
输出格式
根据所输入的问题编号,输出对应问题的答案。
说明/提示
答题模板,可供参考。
cpp
#include<iostream>
using namespace std;
int main() {
string ans [] = {
"The answer of task A", // 双引号中替换为 A 题的答案
"The answer of task B", // 双引号中替换为 B 题的答案
"The answer of task C", // 双引号中替换为 C 题的答案
"The answer of task D", // 双引号中替换为 D 题的答案
"The answer of task E", // 双引号中替换为 E 题的答案
};
char T;
cin >> T;
cout << ans[T - 'A'] << endl;
return 0;
}试题 A :合数个数
合数是啥,合数就是,每个数都有因数。因此数就分为了三部分。
第一部分,质数
质数就是因数只有两个数的数,注意 2 2 2 也是质数。
第二部分,合数
合数就是因数两个以上的数,例如 9 9 9 就是个合数。
第三部分,既不是质数也不是合数
1 1 1 只有 1 1 1 这个因数。
所以,我们知道,我们只需一个 p d pd pd 多少个因数就行。但要特判 1 1 1 这个情况。
用一个判断函数,从 1 1 1 到 2020 2020 2020 遍历判断
cpp
#include<iostream>
using namespace std;
bool pd(int x)
{
if(x<2) return 1;
else
{
for(int i=2;i*i<=x;i++)//注意i*i,不要写成i ,会超时的
{
if(x%i==0) return 1;
}
return 0;
}
}
int main()
{
int ans=0;
for(int i=1;i<=2020;i++)
{
if(pd(i)==1) ans++;
}
cout<<ans;
return 0;
}最后输出 1713 1713 1713 为答案。
试题 B :含 2 天数
我们首先要知道每月天数,这个可以开个 m i m_i mi 来标记。
cpp
int m[13]={0,31,28,31,30,31,30,31,31,30,31,30,31};但是,如果有一年是闰年,二月就会变为 29 29 29 天,所以我们要特判闰年情况。
cpp
if((i%4==0&&i%100!=0)||(i%400==0))
{
m[2]=29;
}
else
{
m[2]=28;
}然后,判断是否有 2 2 2 了,我们从后往前挨个判断。
cpp
while(x>0)
{
int p=x%10;
if(p==2) return 1;
x/=10;
return 0;
}最后的代码。
cpp
#include<bits/stdc++.h>
using namespace std;
int m[13]={0,31,28,31,30,31,30,31,31,30,31,30,31};
int ans=0;
int pd(int x)
{
while(x)
{
if(x%10==2)
{
return 1;
}
x/=10;
}
return 0;
}
int main()
{
for(int i=1900;i<=9999;i++)
{
if((i%4==0&&i%100!=0)||(i%400==0))
{
m[2]=29;
}
else
{
m[2]=28;
}
for(int moon=1;moon<=12;moon++)
{
for(int day=1;day<=m[moon];day++)
{
if(pd(i)||pd(moon)||pd(day))
{
ans++;
}
}
}
}
cout<<ans;
return 0;
}最后输出 1994240 1994240 1994240 为答案。
试题 C :本质上升序列
这是一道动态规划,我们要求出他给定字符串本质不同的单调递增子序列个数。求出 a 1 a_1 a1 一直到 a 200 a_{200} a200 加起来的本质不同的单调递增子序列个数。
cpp
#include<bits/stdc++.h>
using namespace std;
int a[201],ans;
string s="tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhfiadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqijgihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmadvrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhewl";
int main()
{
for(int i=0;i<200;i++)
{
a[i]=1;
for(int j=0;j<i;j++)
{
if(s[i]==s[j])
{
a[i]=0;
}
else if(s[j]<s[i])
{
a[i]+=a[j];
}
}
ans+=a[i];
}
cout<<ans;
return 0;
}试题 D:咫尺天涯
求第 12 12 12 阶皮亚诺曲线中所有相邻格子在曲线上的距离之和。
我们设 f ( k ) f(k) f(k) 为 k k k 阶曲线的距离和。则 f ( k ) = 9 × f ( k − 1 ) + 水平边界距离和 + 垂直边界距离和 f(k)=9×f(k−1)+水平边界距离和+垂直边界距离和 f(k)=9×f(k−1)+水平边界距离和+垂直边界距离和。
边界距离计算使用递归函数计算每个格子在曲线上的坐标,然后对边界上的相邻点计算距离差并求和即可。
结果为: 184731576397539360 184731576397539360 184731576397539360。
试题 E:玩具蛇
运用深度优先搜索,枚举蛇的起点,从起点出发,向四个方向扩展,检查新位置是否在方格内且未被占用。输出即可。
AC代码
cpp
#include<iostream>
using namespace std;
int main() {
string ans [] = {
"1713",
"1994240",
"3616159",
"184731576397539360",
"552",
};
char T;
cin >> T;
cout << ans[T - 'A'] << endl;
return 0;
}