哈喽大家好!我是我不是小upper~
今天想和大家深度拆解一个超实用的技术话题:如何通过融合随机森林、GBDT 与 LightGBM 三大经典树模型,搞定回归预测任务!
我们的核心实战案例,聚焦于大家熟悉的「租金变化预测」场景 ------ 毕竟精准预判租金走势,不管是做数据分析还是实际应用,都是高频需求。
简单来说,这次要分享的核心逻辑很清晰:通过整合这三个特性各异的树模型,既能利用它们的互补优势规避单一模型的偏差局限,又能通过集成策略放大各自的预测亮点,最终实现租金回归预测性能的稳步提升。接下来,就带大家一步步走完这个从模型选型到效果落地的完整流程~
一、业务背景
房屋租金回归预测是典型的结构化数据回归任务 ------ 核心是基于房源的多维特征,精准预测单套房屋的月租金水平。这些特征涵盖了房源的核心属性与周边环境,例如:面积(连续型)、户型(离散型)、楼层(有序型)、朝向(离散型)、装修情况(有序型)、距离地铁的距离(连续型)、所在小区评分(连续型)、城市核心节点距离(地理坐标类)等。
这类问题的复杂性主要体现在四大特点:
- 特征类型混杂:同时包含连续、离散、有序、文本及地理坐标等多种类型,对模型的特征适配能力要求较高;
- 数据噪声与异常值干扰:房源挂牌价与实际成交价存在差异,且短期市场波动可能导致部分异常值,影响模型拟合精度;
- 强非线性与交互效应:例如 "大面积 + 三居室" 的组合对租金的提升效果,或 "核心地段 + 低楼层" 的交互影响,无法通过线性模型有效捕捉;
- 数据分布不平衡:高端房源在样本中占比低,但这类房源的租金水平对整体预测误差的影响显著。
基于以上挑战,本次任务的核心目标是构建一套稳健的回归系统 ------ 不仅要提升租金预测的精准度,还需保证模型具备良好的泛化能力(避免在新样本上表现滑坡)与可解释性(便于理解关键影响因素)。
二、三种核心树模型
在设计融合方案前,需先明确随机森林(RF)、GBDT、LightGBM 三大树模型的核心特性,以及它们在租金回归场景中的适配性 ------ 只有理解单模型的优劣,才能通过融合实现 "取长补短"。
1. 随机森林(Random Forest, RF)
核心原理:基于 Bagging(自助采样集成)思想,通过随机抽取样本与随机选择特征子集,生成多棵独立的决策树,最终对回归任务采用 "多棵树预测结果的平均值" 作为最终输出。
优点:
- 对异常值鲁棒:由于采用多树平均策略,单个异常值对整体预测结果的影响被稀释,适配租金数据中的噪声干扰;
- 无需特征标准化:直接处理原始特征即可,避免了标准化过程中可能引入的信息失真;
- 抗过拟合能力较强(相对单一决策树):多树集成降低了单棵树的方差,且可通过限制树深度进一步优化;
- 支持特征重要性评估:能直观输出各特征对租金预测的贡献度,提升模型可解释性;
- 训练效率高:多棵树可并行训练,便于分布式扩展,适配大规模房源数据。
缺点:
- 拟合复杂非线性能力有限:相比 Boosting 类模型,RF 的 "平均策略" 更保守,对租金数据中强交互效应的捕捉能力不足,可能存在一定偏差;
- 单棵树深度过高时方差增大:若未合理限制树深度,部分决策树可能过度拟合局部样本,导致模型泛化能力下降。
2. GBDT(Gradient Boosting Decision Tree)
核心原理:基于 Boosting(迭代提升)思想,采用 "贪心策略" 逐步拟合前一轮模型的残差 ------ 每一轮训练都针对上一轮的预测误差,通过构建一棵弱学习器(决策树)来修正误差,最终将所有弱学习器的预测结果累加得到最终输出。
优点:
- 强非线性拟合能力:通过迭代修正残差,能精准捕捉租金数据中复杂的非线性关系与特征交互效应(如面积与户型的组合影响),偏差较低;
- 误差修正能力强:可通过设置学习率(步长)控制每棵树的贡献度,逐步优化预测误差,适配租金数据的复杂模式。
缺点:
- 训练速度较慢:串行训练机制(需等待前一棵树训练完成),在大规模房源数据上效率较低;
- 对超参数敏感:树深度、学习率、迭代次数等参数的调整对模型效果影响显著,需大量调参成本;
- 易过拟合:迭代拟合残差的过程可能导致模型过度捕捉训练集噪声,需通过早停、正则化(如限制树深度、叶子节点数)等策略缓解。
3. LightGBM
核心原理:作为 GBDT 的高效工程实现,LightGBM 通过三大核心优化提升性能 ------ 基于直方图(histogram-based)的决策规则(将连续特征离散化为直方图,减少计算量)、梯度单边采样(GOSS,聚焦高梯度样本,提升训练效率)、特征并行与数据并行(优化大规模数据训练速度)。
优点:
- 训练效率极高:相比传统 GBDT,在大规模房源数据上训练速度提升数倍,且内存占用更低;
- 原生支持类别特征:部分版本可直接处理离散类别特征(无需手动编码),适配租金数据中的户型、朝向等特征;
- 预测性能优秀:继承了 GBDT 的强拟合能力,同时通过工程优化降低了过拟合风险,在结构化数据任务中表现稳定。
缺点:
- 小数据 / 高维稀疏数据适配性一般:对于样本量较小或特征高维稀疏的租金数据集,参数调优难度较大,易出现过拟合;
- 对噪声敏感:强拟合能力可能导致模型捕捉训练集中的噪声,需通过正则化(如 L1/L2 正则、叶子节点数限制)进一步优化。
三、融合模型的核心逻辑
集成学习(组合学习)的核心理念是:通过合理组合多个弱学习器,构建性能优于任何单一弱学习器的强学习器。其背后的理论支撑是偏差 - 方差分解------ 回归模型的总体期望误差可拆解为:
其中:
- 偏差(Bias): 模型本身的拟合能力不足导致的误差(如简单模型无法捕捉复杂关系);
- 方差(Variance): 模型对训练数据的波动敏感导致的误差(如复杂模型在不同训练集上表现差异大);
- **不可约误差(Irreducible Error):**由数据本身噪声导致的误差,无法通过模型优化消除。
结合三大树模型的特性,我们可以发现:
- **随机森林(RF):**通过 Bagging 集成降低了方差(多树平均抵消了单树的波动),但偏差相对较高(拟合能力保守,难以捕捉复杂交互);
- **GBDT 与 LightGBM:**通过 Boosting 迭代拟合残差降低了偏差(强拟合能力),但可能导致方差升高(过度拟合训练集细节)。
因此,融合 RF 与 GBDT/LightGBM 的核心逻辑的是:利用模型互补性平衡偏差与方差------ 用 RF 的低方差特性抑制 GBDT/LightGBM 的过拟合风险,同时用 GBDT/LightGBM 的低偏差特性弥补 RF 的拟合不足,最终降低总体期望误差。
从定量角度看,若多个模型的预测误差具有互补性(即误差相关性较低),通过加权平均或堆叠(Stacking)等方式组合,可进一步降低总体误差。例如,简单加权平均下,若模型间误差无相关性,总体方差会按权重平方缩放:
当模型间协方差(误差无相关)时,总体方差仅为各模型方差的加权平方和,若权重合理分配(如按模型性能分配),总体方差会显著降低。
而堆叠(Stacking)则通过训练元学习器学习最优组合方式,不仅能利用线性互补,还能捕捉模型间的非线性互补模式,进一步提升预测性能。
四、三种融合方法
针对租金回归任务,我们选取三种常用且高效的融合策略,以下详细说明其实现要点、优缺点及数学表达:
1. 简单加权平均(Simple Weighted Average)
核心做法
直接对 RF、GBDT、LightGBM 的预测结果按指定权重求和,作为最终预测值。权重的确定基于验证集性能:例如,以各模型在验证集上的 RMSE(均方根误差)倒数为基础进行归一化,性能越优的模型权重越大。
数学表述
设三大基模型的预测结果分别为、
、
,对应的权重为
、
、
(满足
,且
),则最终预测值
为:
其中权重计算示例(基于 RMSE 倒数):
优点与缺点
- 优点:实现简单高效,无需额外训练过程;抗过拟合能力强(权重归一化避免单一模型主导);对噪声数据鲁棒;
- 缺点:仅能捕捉模型间的线性互补关系,无法利用复杂的非线性互补模式;权重分配依赖经验或简单规则,可能未达到最优组合效果。
2. 堆叠集成(Stacking)
核心思路
采用 "两层模型架构":第一层为基模型(RF、GBDT、LightGBM),通过交叉验证生成 "_out-of-fold(OOF)预测特征";第二层为元学习器(Meta-Learner),以 OOF 预测特征为输入,学习最终的预测结果。核心是通过交叉验证避免信息泄露(即基模型未见过的样本用于训练元学习器)。
训练流程(k - 折交叉验证,以 k=5 为例)
- 将训练集随机划分为 5 个互斥的子集(折),记为
;
- 对于每一轮交叉验证(共 5 轮):
- 用除当前折外的 4 个子集(如
)训练基模型(RF、GBDT、LightGBM 各训练一个);
- 用训练好的基模型对当前折(如
)进行预测,得到该折的 OOF 预测值(每个基模型对应 1 列特征);
- 用除当前折外的 4 个子集(如
- 完成 5 轮交叉验证后,将所有折的 OOF 预测值拼接,得到训练集的 "OOF 特征矩阵"(维度为
,
为训练集样本数,3 对应三个基模型);
- 用全部训练数据重新训练三个基模型,然后对测试集进行预测,得到测试集的 "基模型预测特征矩阵"(维度为
,
为测试集样本数);
- 以训练集的 OOF 特征矩阵为输入、真实租金为标签,训练元学习器(如 Lasso、Ridge、LightGBM);
- 用训练好的元学习器,对测试集的基模型预测特征矩阵进行预测,得到最终租金预测值。
数学表述
设基模型集合为,元学习器为g,训练集样本为
(
为真实租金),则:
- 基模型的 OOF 预测特征为:
(
,
为第
个样本在第k个基模型下的 OOF 预测值);
- 元学习器的训练目标为:学习映射关系
;
- 最终预测值为:
。
优点与缺点
- 优点:能自动学习基模型的最优组合方式,支持非线性元学习器(如 LightGBM),可捕捉复杂的互补模式;预测精度通常高于简单加权平均;
- 缺点:实现复杂度高,需严格控制交叉验证流程避免信息泄露;元学习器易过拟合(需加强正则化);训练成本高于简单融合方法。
3. 混合集成(Blending)
核心思路
与 Stacking 类似,同样采用 "基模型 + 元学习器" 的两层架构,但简化了交叉验证流程:直接将训练集划分为 "基础训练集" 和 "验证集"(如 7:3 比例),用基础训练集训练基模型,用基模型对验证集和测试集进行预测,得到 "预测特征",再用验证集的预测特征训练元学习器,最终用元学习器对测试集的预测特征进行预测。
优点与缺点
- 优点:实现逻辑简单,无需复杂的 k - 折交叉验证,训练效率高;避免了 Stacking 中可能出现的信息泄露问题(验证集与基础训练集完全独立);
- 缺点:信息利用率较低(验证集仅用于训练元学习器,未参与基模型训练);相比 Stacking,泛化能力可能稍弱(基模型未经过交叉验证优化)。
五、评价指标与交叉验证设计
1. 核心评价指标(回归任务专用)
为全面评估租金预测模型的性能,选取以下 4 个常用回归指标,从不同维度衡量预测误差:
(1)均方误差(Mean Squared Error, MSE)
衡量预测值与真实值的平方误差的平均值,对大误差样本惩罚更显著(平方项放大误差):
其中为第
个样本的预测租金,
为真实租金,n为样本数。
(2)均方根误差(Root Mean Squared Error, RMSE)
MSE 的平方根,与目标变量(租金)同量级,更易直观解释(如 RMSE=500 表示平均预测误差为 500 元):
(3)平均绝对误差(Mean Absolute Error, MAE)
衡量预测值与真实值的绝对误差的平均值,对异常值的惩罚相对温和(无平方项):
(4)决定系数(R² Score)
衡量模型对数据的解释能力,取值范围为,R² 越接近 1 表示模型拟合效果越好(完美拟合时 R²=1):
其中为真实租金的平均值。
2. 交叉验证(CV)策略
交叉验证的核心目的是避免模型过拟合,同时稳定评估模型的泛化能力,针对租金数据的特点设计以下策略:
(1)普通 K-Fold 交叉验证
适用于无时间依赖性的租金数据(如随机收集的跨时间房源样本):将数据集随机划分为 k 个折(常用 k=5 或 10),按 "k-1 折训练、1 折验证" 的方式迭代 k 次,最终取 k 次验证的指标平均值作为模型性能评估结果。
(2)时间序列交叉验证(TimeSeriesSplit)
若租金数据存在时间依赖性(如不同月份的租金受市场趋势影响),则需采用时间序列交叉验证:将数据按时间顺序划分(如按月份排序),第 1 次用前 10% 数据训练、10%-20% 数据验证,第 2 次用前 20% 数据训练、20%-30% 数据验证,以此类推,避免 "未来数据泄露到训练集" 的问题(符合租金预测的实际场景:用历史数据预测未来租金)。
(3)融合场景下的 CV 设计
为确保 Stacking/Blending 中 OOF 特征的稳定性,建议采用 k=5 或 10 折交叉验证 ------ 折数越多,OOF 特征的统计代表性越强,元学习器的训练效果越稳定;同时,所有基模型需使用相同的交叉验证划分方式,避免因数据划分差异导致的预测特征不一致。
完整案例
我们在房屋租金场景中,为了更好的贴合实际情况,构造下面的数据~
-
基础特征:面积(
)、卧室数、厅数、卫数、楼层、总楼层、朝向、装修等级。
-
地理相关:经纬度(可做网格/聚类)、距离最近地铁站、商圈密度、到市中心距离。
-
社区信息:小区均价、小区评分、房龄、物业类型、安全性评分。
-
时间特征:挂牌时间、季节、月份、节假日。
-
文本与图片:房源描述可做文本情感/关键词提取;图片特征可通过 CNN 提取(本文不包含)。
-
交互特征:面积×户型、地铁距离×楼层、朝向×楼层(采光)、装修×小区均价。
-
缺失值处理:类别缺失用 "Unknown" 或填充中位数;连续值用中位数或基于最近邻插值。
-
离群值处理:房租或面积异常时,使用对数变换或截断。
通常对租金做对数变换会更稳定:
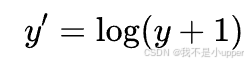
超参数调优
常用方法:
-
网格搜索:适合少量关键参数。
-
随机搜索:高效,适合大参数空间。
-
贝叶斯优化:样本效率高,效果好。
关键超参数示例:
-
随机森林:n_estimators(树数),max_depth,max_features,min_samples_split,min_samples_leaf。
-
GBDT(sklearn):n_estimators,learning_rate,max_depth,min_samples_split。
-
LightGBM:num_leaves,max_depth,learning_rate,n_estimators,feature_fraction,bagging_fraction,lambda_l1,lambda_l2,min_data_in_leaf。
调优技巧方面:
-
先固定学习率,并调整树结构参数(num_leaves、max_depth)。
-
再调学习率与 n_estimators;较小的学习率+较大的树数通常更稳健。
-
使用早停(early_stopping_rounds)防止过拟合。
-
对特征选择可用递归特征消除或基于特征重要性阈值筛选。
代码框架
整体流程:
-
数据读取与清洗
-
初步探索与可视化(分布、相关性)
-
特征构造与编码(类别编码/数值化)
-
划分训练/验证/测试或使用 CV
-
基模型训练(RF、GBDT、LightGBM),保存 OOF 预测
-
训练元学习器(stacking)或进行加权平均
-
模型评估与可解释性分析(特征重要性、SHAP)
-
上线部署(模型版本控制、定期重训)
python
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor
from sklearn.model_selection import KFold, train_test_split
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
from sklearn.linear_model import Ridge
import lightgbm as lgb
import joblib
import warnings
warnings.filterwarnings('ignore')
# 1. Generate synthetic dataset (simulate house rent data)
np.random.seed(42)
N = 8000
# Basic features
area = np.random.normal(70, 25, N).clip(20, 300) # Building area (square meters)
bedrooms = np.random.choice([1,2,3,4], size=N, p=[0.2,0.45,0.25,0.1]) # Number of bedrooms
floor = np.random.randint(1, 30, N) # Current floor
total_floor = floor + np.random.randint(0, 10, N) # Total floors of the building
age = np.random.exponential(10, N).clip(0,80) # House age (years)
distance_metro = np.abs(np.random.normal(800, 600, N)).clip(50, 5000) # Distance to nearest metro (meters)
district_level = np.random.choice([1,2,3,4,5], size=N, p=[0.1,0.2,0.4,0.2,0.1]) # District grade (1-5, higher=better)
furnish = np.random.choice(['none','simple','fine','luxury'], size=N, p=[0.15,0.5,0.25,0.1]) # Decoration level
season = np.random.choice(['spring','summer','autumn','winter'], size=N) # Listing season
lat = np.random.uniform(40.0, 40.2, N) + (district_level-3)*0.01 # Latitude (simplified offset by district)
lon = np.random.uniform(116.0, 116.2, N) + (district_level-3)*0.01 # Longitude (simplified offset by district)
# Generate base rent function (artificial non-linear + interaction effects)
base = 20 * np.sqrt(area) # Area contribution (non-linear)
bedroom_factor = bedrooms * 80 # Bedroom number contribution
# High floor near top affects lighting (example interaction)
floor_factor = np.where(floor/total_floor > 0.6, -30, 0)
age_factor = -np.log1p(age) * 40 # House age contribution (older=cheaper)
metro_factor = -0.02 * distance_metro # Metro distance contribution (farther=cheaper)
district_factor = district_level * 120 # District grade contribution (higher=more expensive)
# Decoration level mapping
furnish_map = {'none': -100, 'simple': 0, 'fine': 150, 'luxury': 400}
furnish_factor = [furnish_map[x] for x in furnish]
# Season factor (winter=cheaper, summer=more expensive)
season_factor = np.where(season=='winter', -20, np.where(season=='summer', 10, 0))
# Combine all factors and add random noise + outliers
price = (base + bedroom_factor + floor_factor + age_factor + metro_factor +
district_factor + np.array(furnish_factor) + season_factor +
np.random.normal(0, 120, N))
# Add a small number of extreme high-price samples
high_idx = np.random.choice(N, size=int(N*0.02), replace=False)
price[high_idx] *= np.random.uniform(1.8, 3.5, size=len(high_idx))
# Ensure rent is positive
price = np.maximum(price, 200)
# Build DataFrame
df = pd.DataFrame({
'area': area,
'bedrooms': bedrooms,
'floor': floor,
'total_floor': total_floor,
'age': age,
'distance_metro': distance_metro,
'district_level': district_level,
'furnish': furnish,
'season': season,
'lat': lat,
'lon': lon,
'rent': price
})
# Log transformation for target (common practice for regression stability)
df['log_rent'] = np.log1p(df['rent'])
# 2. Initial visualization
sns.set(style='whitegrid', context='talk')
# Plot 1: Rent distribution (original & log-transformed)
plt.figure(figsize=(14,5))
plt.subplot(1,2,1)
sns.histplot(df['rent'], bins=60, kde=True, color='#FF6F61')
plt.title("Distribution of House Rent (Original)")
plt.xlabel("Monthly Rent (Yuan)")
plt.subplot(1,2,2)
sns.histplot(df['log_rent'], bins=60, kde=True, color='#6B5B95')
plt.title("Distribution of House Rent (Log-Transformed)")
plt.xlabel("log(Monthly Rent + 1)")
plt.tight_layout()
plt.show()
# Plot 2: Correlation heatmap of numerical features (including log_rent)
plt.figure(figsize=(10,8))
num_cols = ['area','bedrooms','floor','total_floor','age','distance_metro','district_level','lat','lon','rent','log_rent']
corr = df[num_cols].corr()
sns.heatmap(corr, annot=True, cmap='RdYlBu_r', vmax=1, vmin=-1)
plt.title("Correlation Heatmap of Numerical Features")
plt.tight_layout()
plt.show()
# 3. Feature processing & train-test split
# Categorical encoding (one-hot, drop first to avoid multicollinearity)
df_encoded = df.copy()
df_encoded = pd.get_dummies(df_encoded, columns=['furnish','season'], drop_first=True)
# Select features (exclude target variables)
# Fix syntax error: 'notin' -> 'not in'
features = [c for c in df_encoded.columns if c not in ['rent','log_rent']]
X = df_encoded[features].values
y = df_encoded['log_rent'].values # Use log-transformed target for training
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 4. Train three base models and generate OOF predictions (simplified version with KFold)
n_splits = 5
kf = KFold(n_splits=n_splits, shuffle=True, random_state=42)
oof_preds = {
'rf': np.zeros(len(y_train)),
'gbdt': np.zeros(len(y_train)),
'lgb': np.zeros(len(y_train))
}
test_preds = {
'rf': np.zeros(len(y_test)),
'gbdt': np.zeros(len(y_test)),
'lgb': np.zeros(len(y_test))
}
# Base hyperparameters (not tuned for example purposes)
rf_params = {'n_estimators':200, 'max_depth':12, 'n_jobs':-1, 'random_state':42}
gbdt_params = {'n_estimators':500, 'learning_rate':0.05, 'max_depth':5, 'random_state':42}
lgb_params = {
'objective':'regression',
'learning_rate':0.03,
'num_leaves':31,
'random_state':42,
'verbose':-1 # Remove n_estimators, use num_boost_round in train()
}
# Store best iterations for LGBM (to use in full train later)
lgb_best_iterations = []
for fold, (tr_idx, val_idx) in enumerate(kf.split(X_train)):
print(f"Fold {fold+1}")
X_tr, X_val = X_train[tr_idx], X_train[val_idx]
y_tr, y_val = y_train[tr_idx], y_train[val_idx]
# Random Forest
rf = RandomForestRegressor(**rf_params)
rf.fit(X_tr, y_tr)
oof_preds['rf'][val_idx] = rf.predict(X_val)
test_preds['rf'] += rf.predict(X_test) / n_splits
# GBDT
gbdt = GradientBoostingRegressor(**gbdt_params)
gbdt.fit(X_tr, y_tr)
oof_preds['gbdt'][val_idx] = gbdt.predict(X_val)
test_preds['gbdt'] += gbdt.predict(X_test) / n_splits
# LightGBM (fix: use callbacks for early stopping and verbose)
lgb_train = lgb.Dataset(X_tr, label=y_tr, free_raw_data=False)
lgb_val = lgb.Dataset(X_val, label=y_val, reference=lgb_train, free_raw_data=False)
# Define callbacks: early stopping + disable log output
callbacks = [
lgb.early_stopping(stopping_rounds=50, verbose=False), # Early stopping (50 rounds)
lgb.log_evaluation(0) # Disable log output (0 = no evaluation logs)
]
lgbm = lgb.train(
lgb_params,
lgb_train,
num_boost_round=1000, # Replace n_estimators with num_boost_round
valid_sets=[lgb_train, lgb_val],
callbacks=callbacks # Pass callbacks instead of direct params
)
# Save best iteration for later use
lgb_best_iterations.append(lgbm.best_iteration)
oof_preds['lgb'][val_idx] = lgbm.predict(X_val, num_iteration=lgbm.best_iteration)
test_preds['lgb'] += lgbm.predict(X_test, num_iteration=lgbm.best_iteration) / n_splits
# Merge OOF features for meta-learner
X_meta_train = np.vstack([oof_preds['rf'], oof_preds['gbdt'], oof_preds['lgb']]).T
X_meta_test = np.vstack([test_preds['rf'], test_preds['gbdt'], test_preds['lgb']]).T
# 5. Train meta-learner (simple linear regression: Ridge)
meta_model = Ridge(alpha=1.0)
meta_model.fit(X_meta_train, y_train)
meta_pred = meta_model.predict(X_meta_test)
# Train full base models on entire training set (for baseline comparison)
# Random Forest full train
rf_final = RandomForestRegressor(**rf_params)
rf_final.fit(X_train, y_train)
rf_test = rf_final.predict(X_test)
# GBDT full train
gbdt_final = GradientBoostingRegressor(**gbdt_params)
gbdt_final.fit(X_train, y_train)
gbdt_test = gbdt_final.predict(X_test)
# LightGBM full train (use average of best iterations from CV)
lgb_full = lgb.Dataset(X_train, label=y_train, free_raw_data=False)
# Use average of best iterations to avoid single fold bias
avg_best_iter = int(np.mean(lgb_best_iterations))
# Define callbacks for full train (optional: no early stopping, just log off)
full_callbacks = [lgb.log_evaluation(0)]
lgbm_final = lgb.train(
lgb_params,
lgb_full,
num_boost_round=avg_best_iter, # Use average best iteration from CV
callbacks=full_callbacks
)
lgb_test = lgbm_final.predict(X_test)
# 6. Evaluation function
def eval_all(y_true, preds_dict):
"""Evaluate multiple models with regression metrics"""
for k, v in preds_dict.items():
mse = mean_squared_error(y_true, v)
rmse = np.sqrt(mse)
mae = mean_absolute_error(y_true, v)
r2 = r2_score(y_true, v)
print(f"{k} -> RMSE: {rmse:.4f}, MAE: {mae:.4f}, R2: {r2:.4f}")
# Prepare prediction dictionary for evaluation
preds_dict = {
'rf': rf_test,
'gbdt': gbdt_test,
'lgb': lgb_test,
'stacking_meta': meta_pred,
'simple_avg': (rf_test + gbdt_test + lgb_test) / 3
}
print("\nEvaluation (Target: log_rent):")
eval_all(y_test, preds_dict)
# 7. Visualization 3: Feature importance comparison (Top 12 features)
# Get feature importance from three models
rf_imp = rf_final.feature_importances_
gbdt_imp = gbdt_final.feature_importances_
lgb_imp = lgbm_final.feature_importance(importance_type='gain')
# Create importance DataFrame
imp_df = pd.DataFrame({
'feature': features,
'rf': rf_imp,
'gbdt': gbdt_imp,
'lgb': lgb_imp
})
# Select top 12 features by maximum importance across models
imp_df['max_imp'] = imp_df[['rf','gbdt','lgb']].max(axis=1)
imp_top = imp_df.sort_values('max_imp', ascending=False).head(12).set_index('feature')
# Normalize importance (per model, sum to 1)
imp_top_norm = imp_top[['rf','gbdt','lgb']].apply(lambda x: x / (x.sum()+1e-9), axis=0)
plt.figure(figsize=(12,6))
imp_top_norm.plot(kind='bar', color=['#FF7F50','#6A5ACD','#20B2AA'])
plt.title("Feature Importance Comparison (Top 12, Normalized)")
plt.ylabel("Normalized Importance")
plt.xticks(rotation=45, ha='right')
plt.tight_layout()
plt.show()
# 8. Visualization 4: Predicted vs True values (scatter plot)
plt.figure(figsize=(8,8))
sc = plt.scatter(y_test, meta_pred, c=meta_pred-y_test, cmap='coolwarm', alpha=0.6, s=20)
plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'k--', lw=2)
plt.colorbar(sc, label='Predicted - True (log scale)')
plt.xlabel("True log_rent")
plt.ylabel("Stacking Meta-Model Predicted log_rent")
plt.title("Predicted vs True Values (Stacking Meta-Model)")
plt.tight_layout()
plt.show()
# 9. Visualization 5: Residual analysis
residuals = meta_pred - y_test
plt.figure(figsize=(10,5))
plt.subplot(1,2,1)
sns.histplot(residuals, bins=50, kde=True, color='#FFB347')
plt.title("Residual Distribution (Stacking Model)")
plt.xlabel("Residuals (pred - true)")
plt.subplot(1,2,2)
sns.scatterplot(x=meta_pred, y=residuals, hue=np.abs(residuals), palette='Spectral', legend=False, s=20)
plt.axhline(0, color='k', linestyle='--')
plt.xlabel("Predicted Values (log)")
plt.ylabel("Residuals")
plt.title("Residuals vs Predicted Values (Color by Residual Magnitude)")
plt.tight_layout()
plt.show()
# 10. Optional: SHAP analysis (requires shap library installed)
# Add exception handling to avoid ModuleNotFoundError
try:
import shap
# Use a subset of test data for faster computation
sample_size = 1000
X_test_sample = X_test[:sample_size]
feature_names_sample = features
# SHAP explainer for LightGBM
explainer = shap.TreeExplainer(lgbm_final)
shap_values = explainer.shap_values(X_test_sample)
# Plot SHAP summary
plt.figure(figsize=(10,6))
shap.summary_plot(shap_values, pd.DataFrame(X_test_sample, columns=feature_names_sample), show=False, plot_type='dot')
plt.title("LightGBM Feature SHAP Values (Sample Data)")
plt.tight_layout()
plt.show()
except ImportError:
print("\nNote: SHAP library is not installed. Please install it with 'pip install shap' to run the SHAP analysis.")房屋租金分布(原始 & 对数):
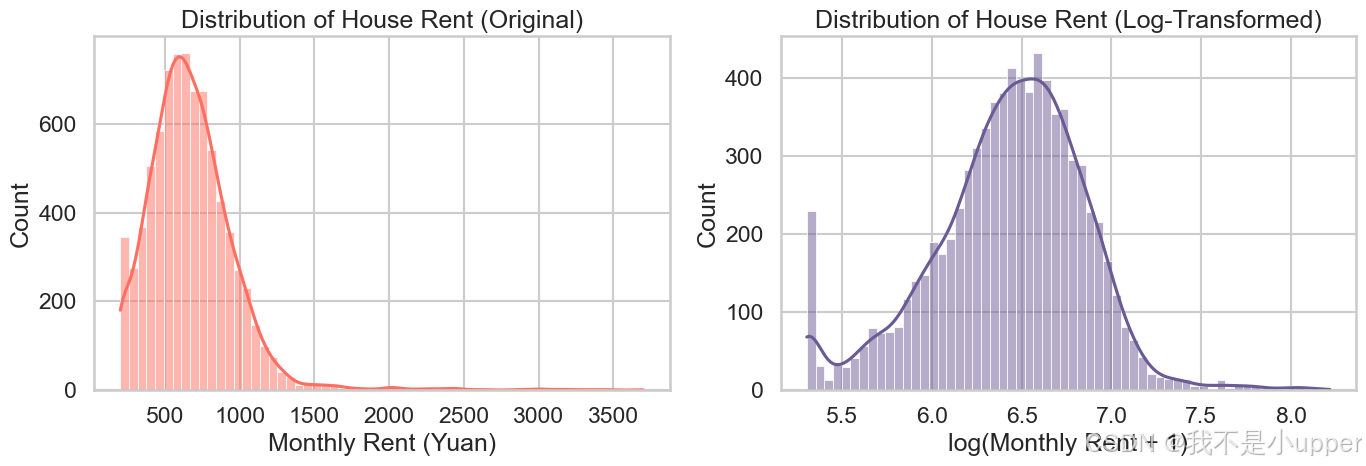
展示租金的总体分布形态与偏度。原始租金通常右偏(长尾),存在少量高价样本;对数变换后更接近正态分布,利于回归模型稳定训练。
对数变换能降低长尾影响,MSE/MAE 等指标更稳定,模型更容易学习。
特征相关性热力图:
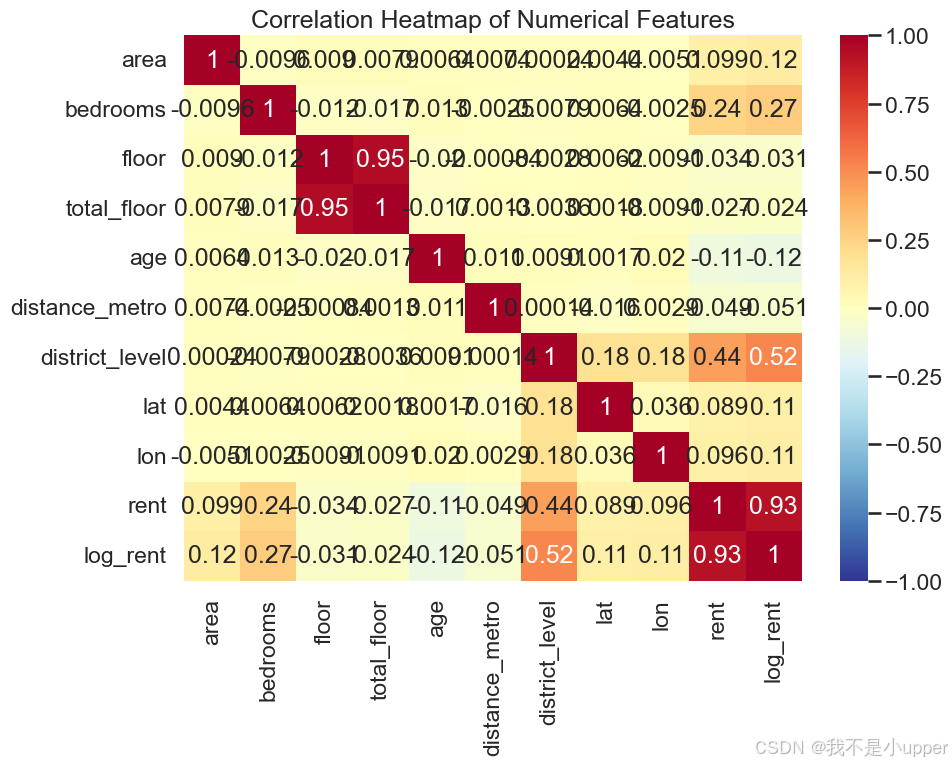
展示数值特征之间的线性相关性。可以发现面积、卧室数、经纬度与租金相关,距离地铁与租金呈负相关等。
帮助初步筛选特征与构造交互项。例如若 area 与 rent 相关性高,可尝试 area 的幂次或分段处理。
三模型特征重要性对比(Top12):
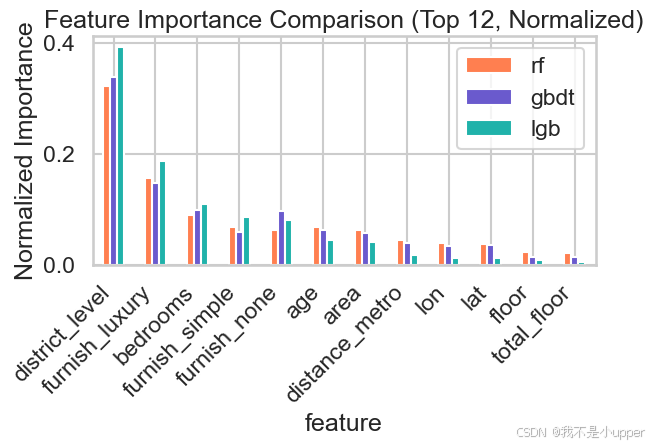
比较 RF、GBDT、LightGBM 在特征选择上的偏好。不同算法可能对同一特征赋予不同权重(例如 RF 偏好 high-cardinality 的分裂,GBDT/LightGBM 更注重非线性交互)。
如果某特征在一个模型中权重高而在其他模型中低,说明该特征能带来模型互补性。可以在 stacking 中保留这些多样化的视角。
预测值 vs 真实值:
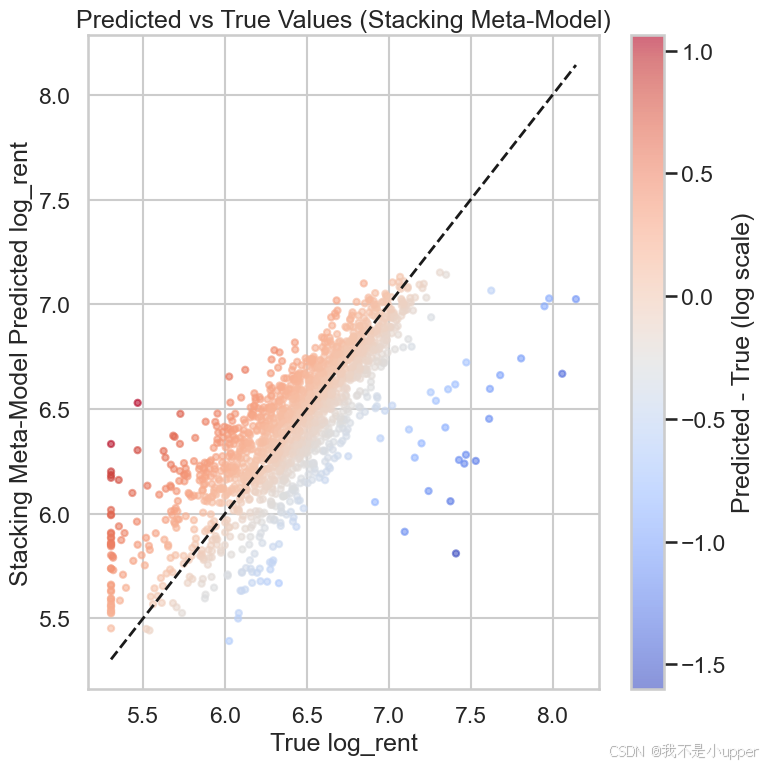
直观检查模型预测准确性与偏差。理想点应接近 y=x 对角线。颜色映射显示预测误差大小与方向。
大批点聚集在对角线附近表示总体拟合良好;若在某个区间(例如高价房)误差趋大,说明模型在长尾/稀疏样本上欠拟合或样本不足。
残差分析:
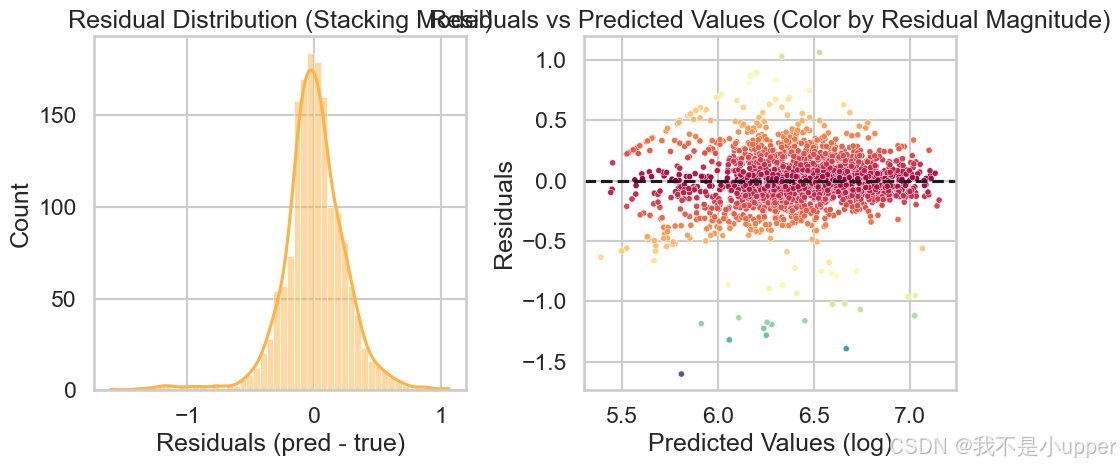
检查残差是否近似零均值、是否存在异方差(residual variance 随预测值变化)。
若残差呈现系统性偏差(例如在高预测值处偏正),说明模型存在欠拟合或特征不足,需进一步建模(如加入更多交互项、非线性特征或对高端房源做专门子模型)。
SHAP summary(LightGBM):
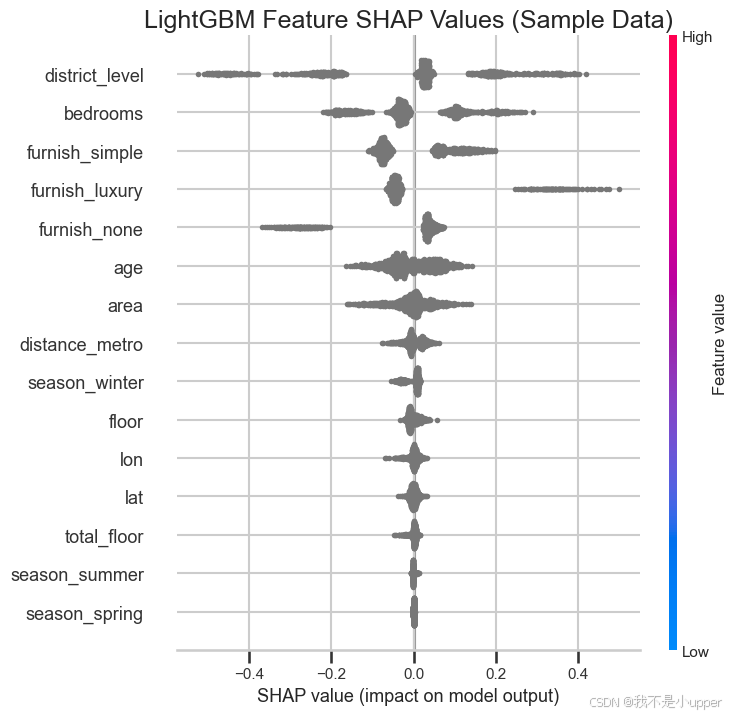
SHAP 值展示每个特征对模型输出的贡献方向与分布。颜色代表原始特征值大小,点的分布代表贡献大小和一致性。
可解释模型,帮助产品/运营理解哪些特征驱动租金变化,例如小区等级、地铁距离、装修水平等。
在本例中,单模型在 log_rent 指标上各有表现,而通过 Stacking 融合的模型在多数指标(RMSE/MAE/R^2)上取得提升(具体数值见代码运行后的输出)。
原因在于,RF 提供低方差的预测基线(稳定),GBDT/LightGBM 擅长捕捉复杂非线性交互,stacking 将它们的优点结合且由元学习器校准偏差,取得更好泛化。
总结
三类树模型互补:RF(低方差)、GBDT(较低偏差)、LightGBM(高效训练),合理融合能显著提升房屋租金回归效果。
融合策略选择方面,若资源有限,先用简单加权平均;若追求性能,采用 Stacking 并用交叉验证生成 OOF 特征。
特征工程这个是大家要着重注意的,高质量的特征(地理聚合、交互、时间序列特征)往往比模型调参带来更大提升。
最后大家可以拿自己的数据或者实际业务情况,试试看~