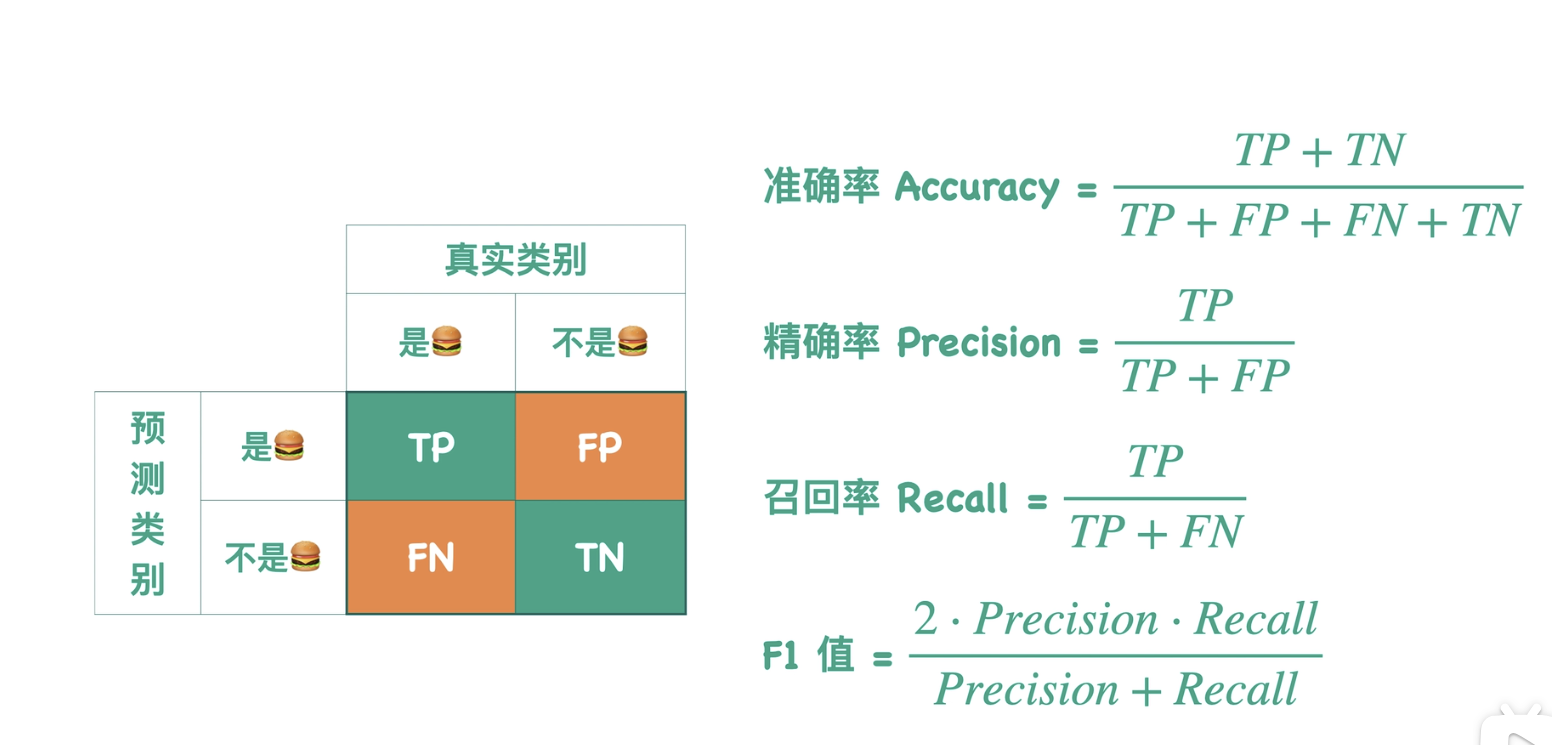
一.混淆矩阵,准确率,精确率,召回率,F1
【小萌五分钟】机器学习 | 混淆矩阵 Confusion Matrix_哔哩哔哩_bilibili
混淆矩阵:
二分类:
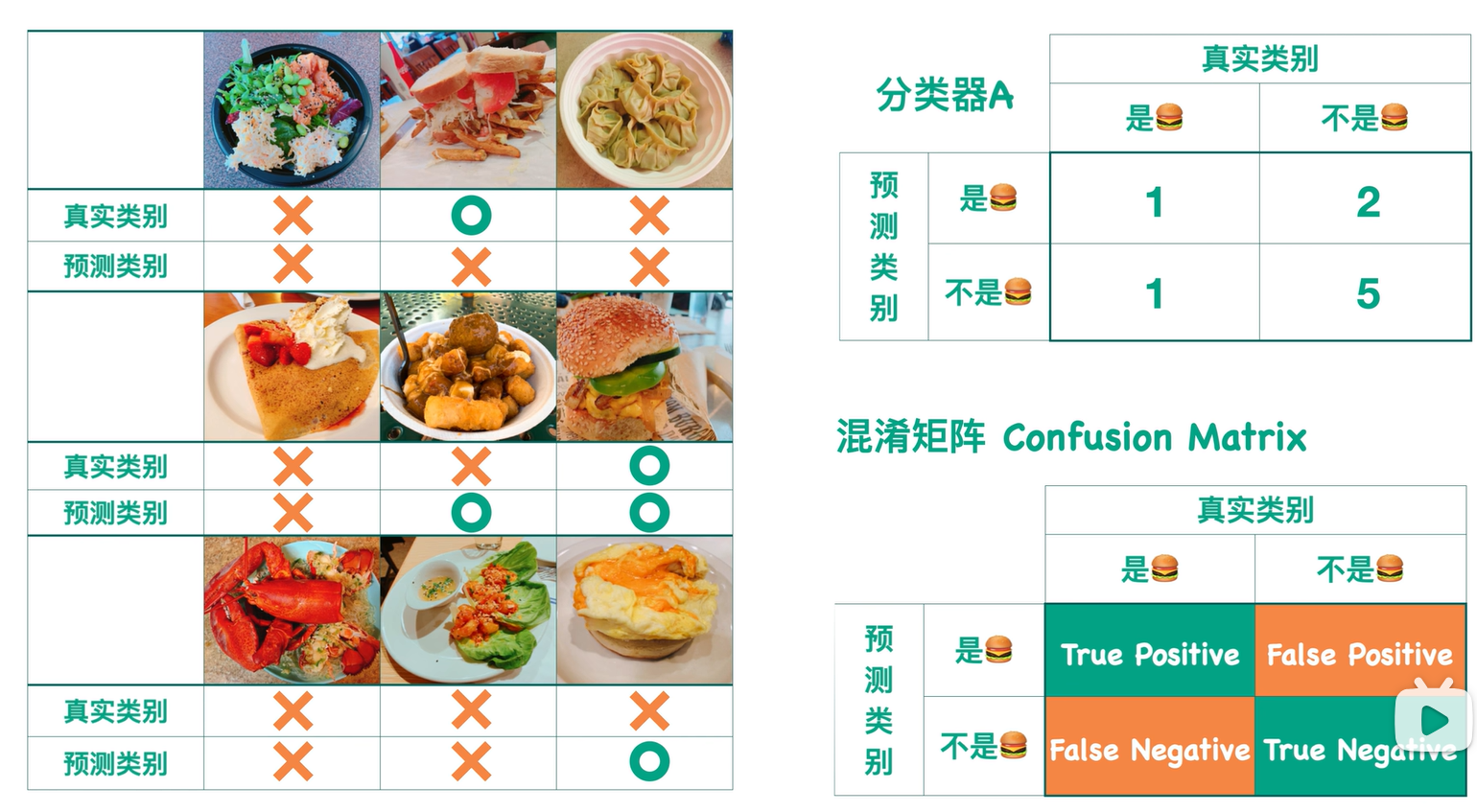
上图是分类器在测试集上的效果:
- True:预测类别和真实类别一致。
- False:预测类别和真实类别不一致。
- Positive:预测类别把样本预测成Positive类。
- Negative:预测类别把样本预测成Negative类。
TP,FP,FN,TN
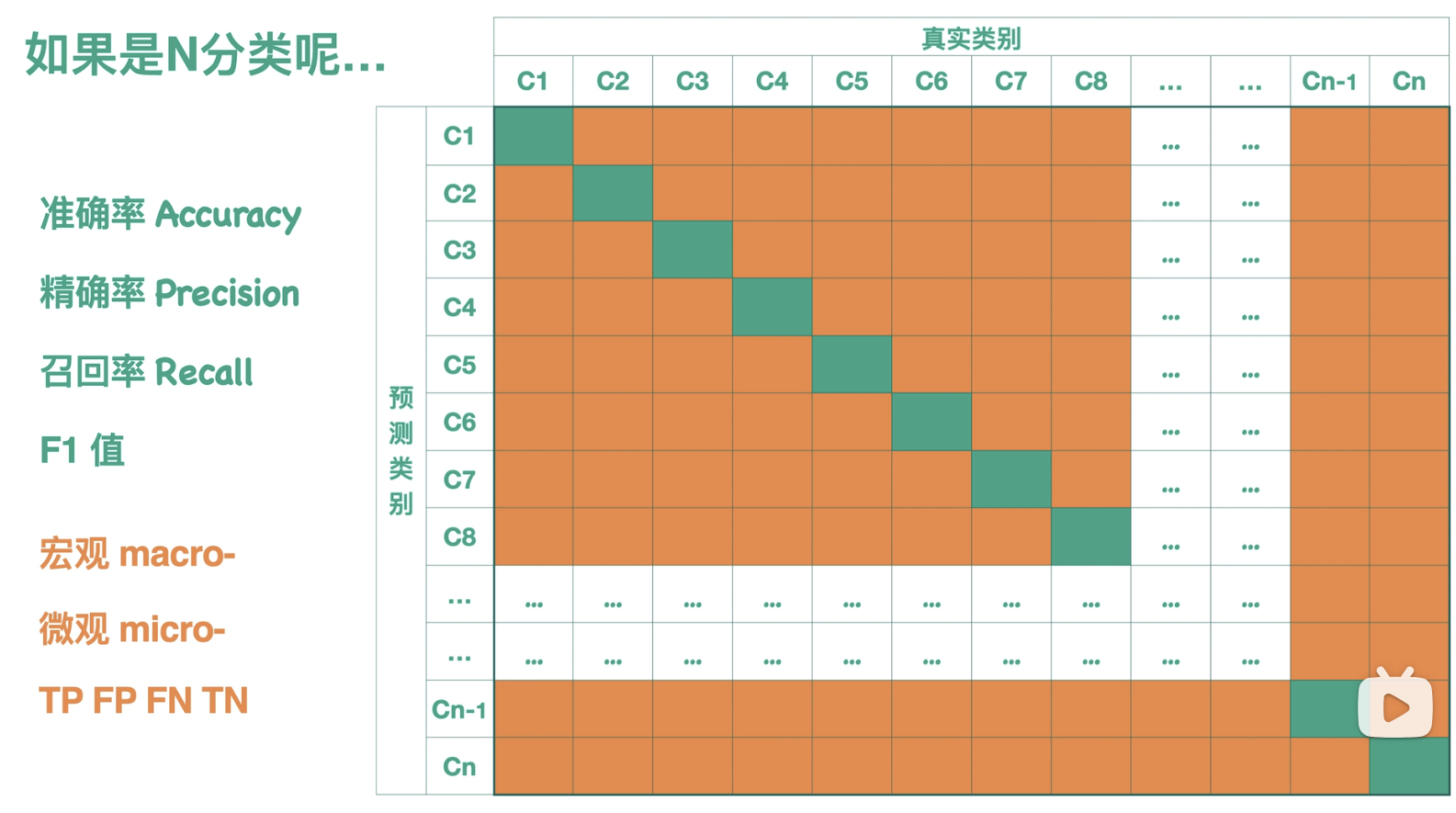
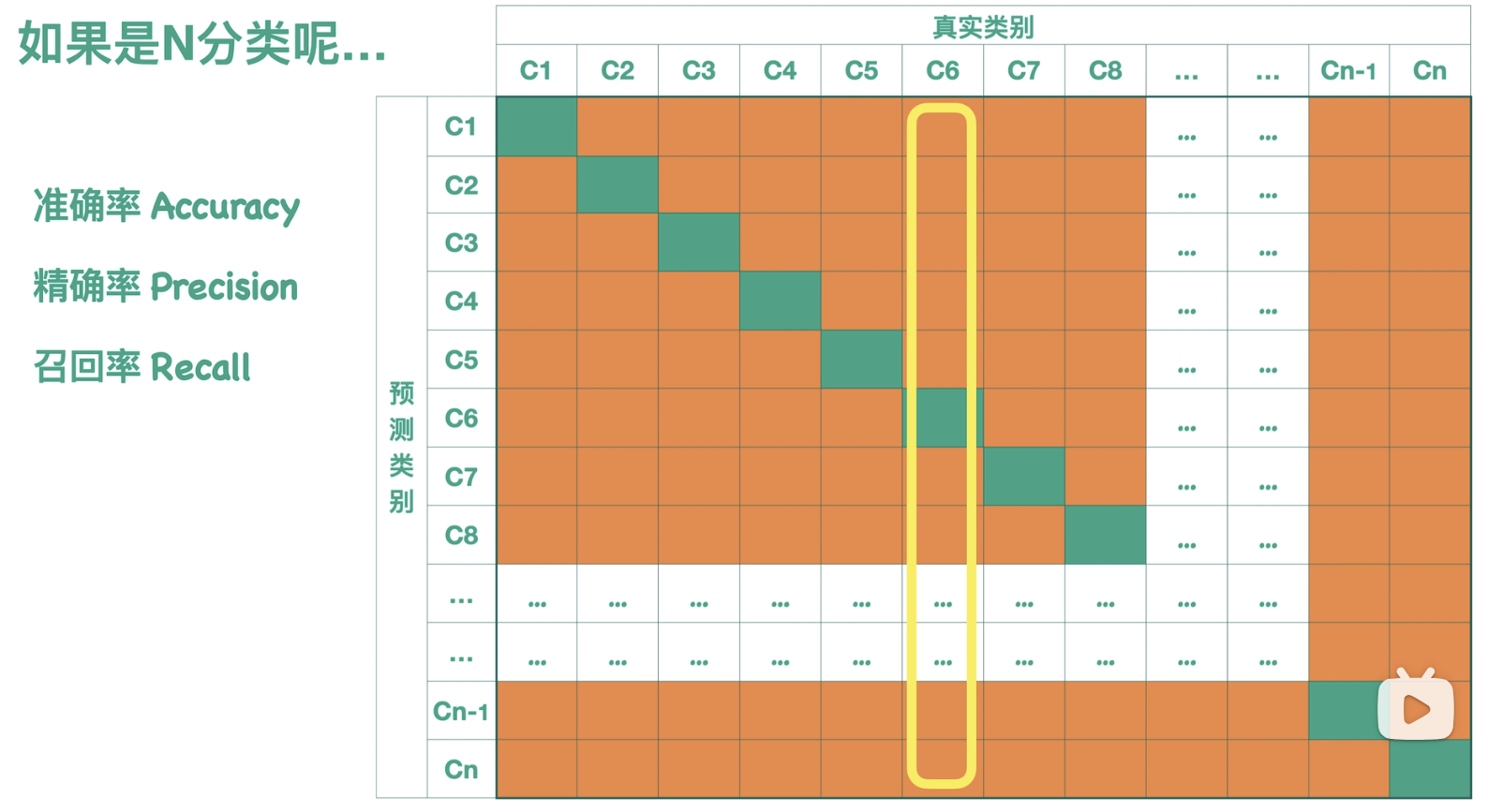
多分类:
如果说二分类 是通过图片分类器预测样本是不是 汉堡,那么多分类 就是通过图片分类器预测样本的类别(是甜甜圈/汉堡/薯条?):
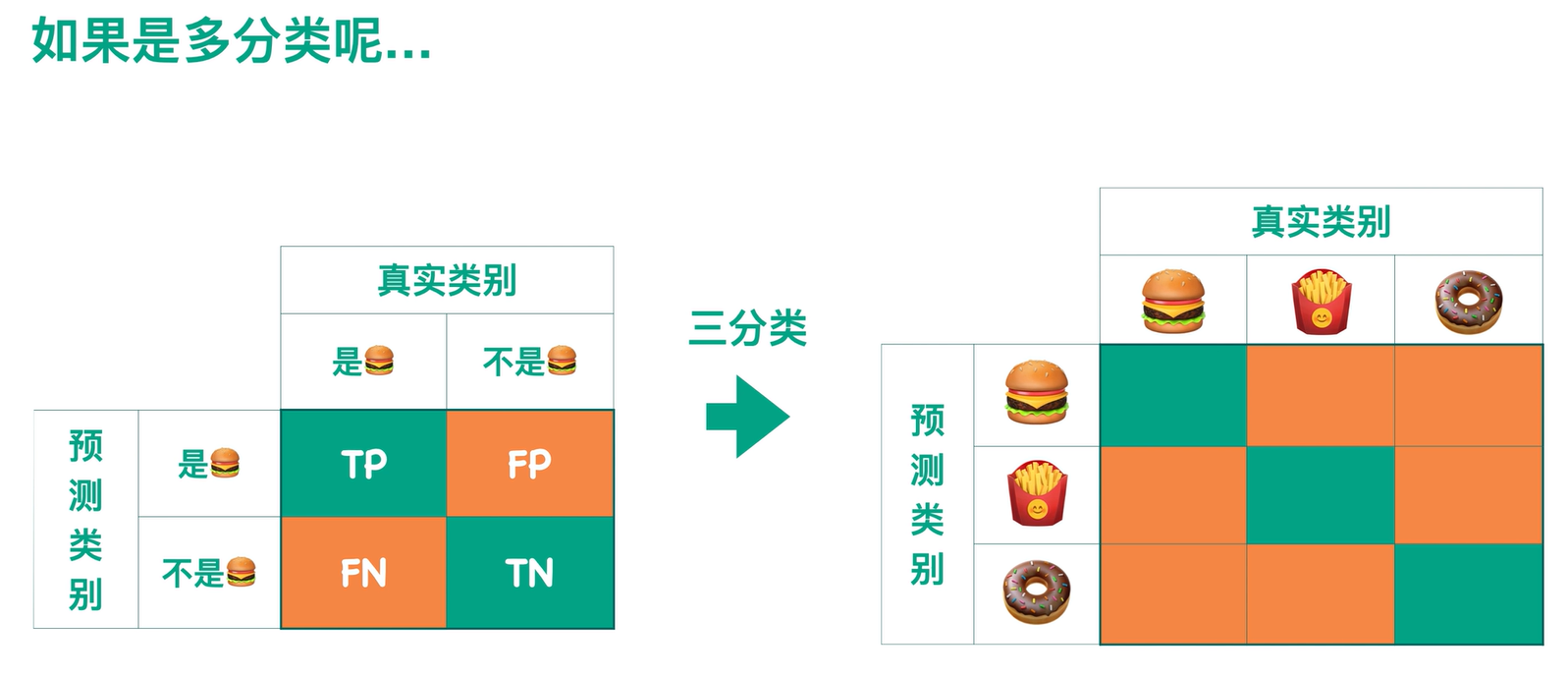
与二分类相同,图形左上角到右下角的对角线(绿色部分)表示图形预测正确的情况的个数统计。
而剩下的橙色部分是模型预测错误的情况的个数统计。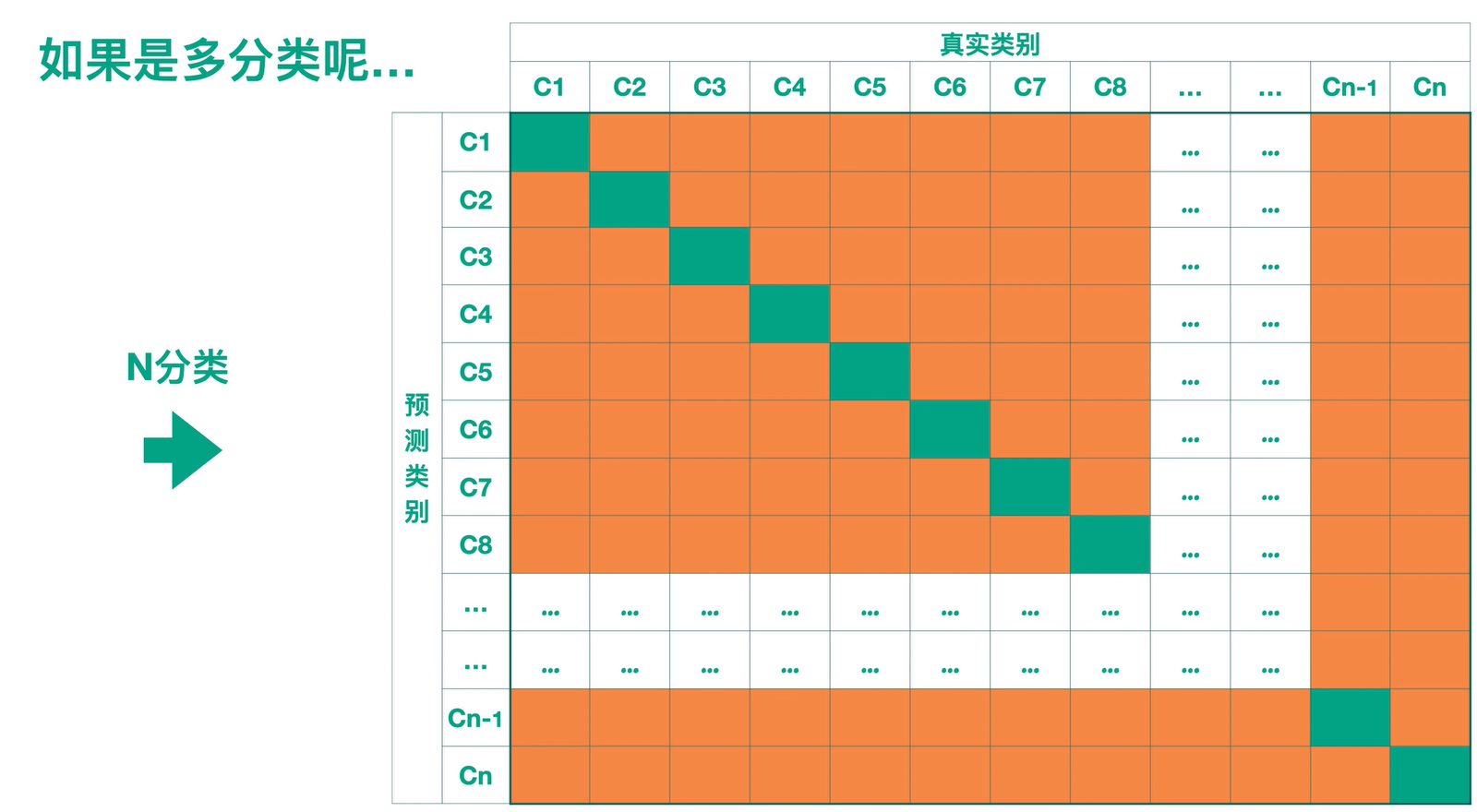
所以希望绿色部分尽可能大,橙色部分尽可能小时,模型预测效果好。
评估指标:
得到混淆矩阵以后,我们可以根据混淆矩阵衍生出一些指标来评估模型效果:
二分类:
- 准确率(Accuracy):
分类器分对了多少?
=(真实类别与预测类别相同的汉堡数/测试集整体的汉堡总数)
- 精确率(Precision):
假设有一个汉堡图片搜索引擎,返回的图片中正确的有多少?
=(返回图片中是汉堡的图片数/返回图片总数)
- 召回率(Recall):
假设有一个汉堡图片搜索引擎,有多少张应该返回的图片没有找到?
=(返回图片中是汉堡的图片数/测试集整体的汉堡总数)

- F1:
精确率和召回率:在某种程度上,此消彼长,所以不能一味的要求某一方高,为了解决这个问题引出新参数F1。
注:F1是当取beta=1时(即认为recall和accuracy值同等重要时)的FB值。

根据刚才的整个计算过程,我们可以抽象得到针对二分类的指标的计算公式:
精确率和召回率:在某种程度上,此消彼长。
假设一种极端情况,汉堡图片搜索引擎返回测试集中所有图片:
则此时精确率很低,召回率很高。
多分类:
多分类每一类的指标参数的计算:
- 准确率(Accuracy):
准确率就是图中所有薄荷绿的部分的方块总数,然后再除以样本的总数,样本总数就是图中所有方块求和。
- 精确率(Precision):
精确率我们往往对于多分类来说,我们可以单独的看每一类 。比如说我们看 c6 这一类,那么它的精确率就是它分对的情况,除以这一行的样本总数,而它的召回率 就是它分对的情况,除以这一列的样本总数。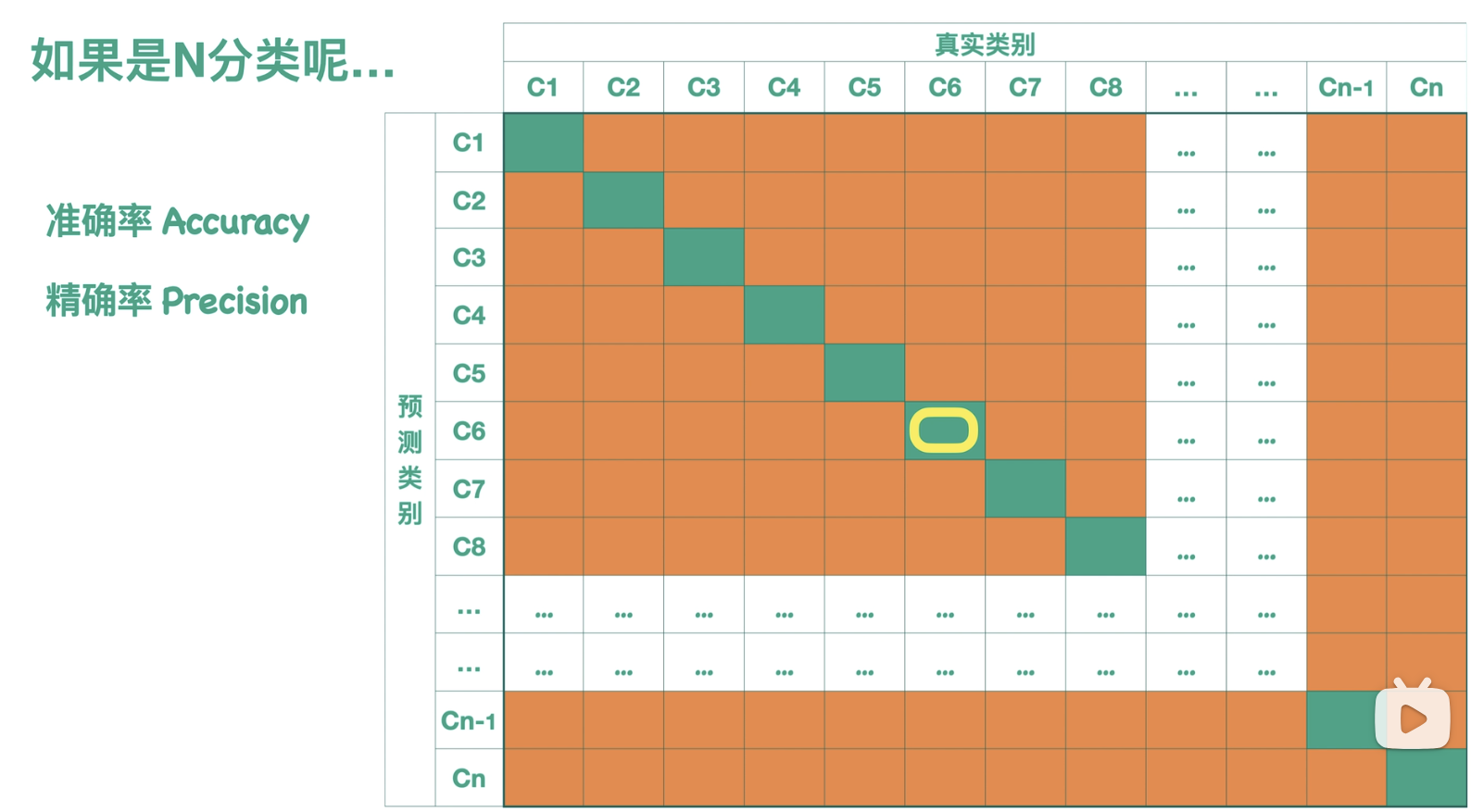
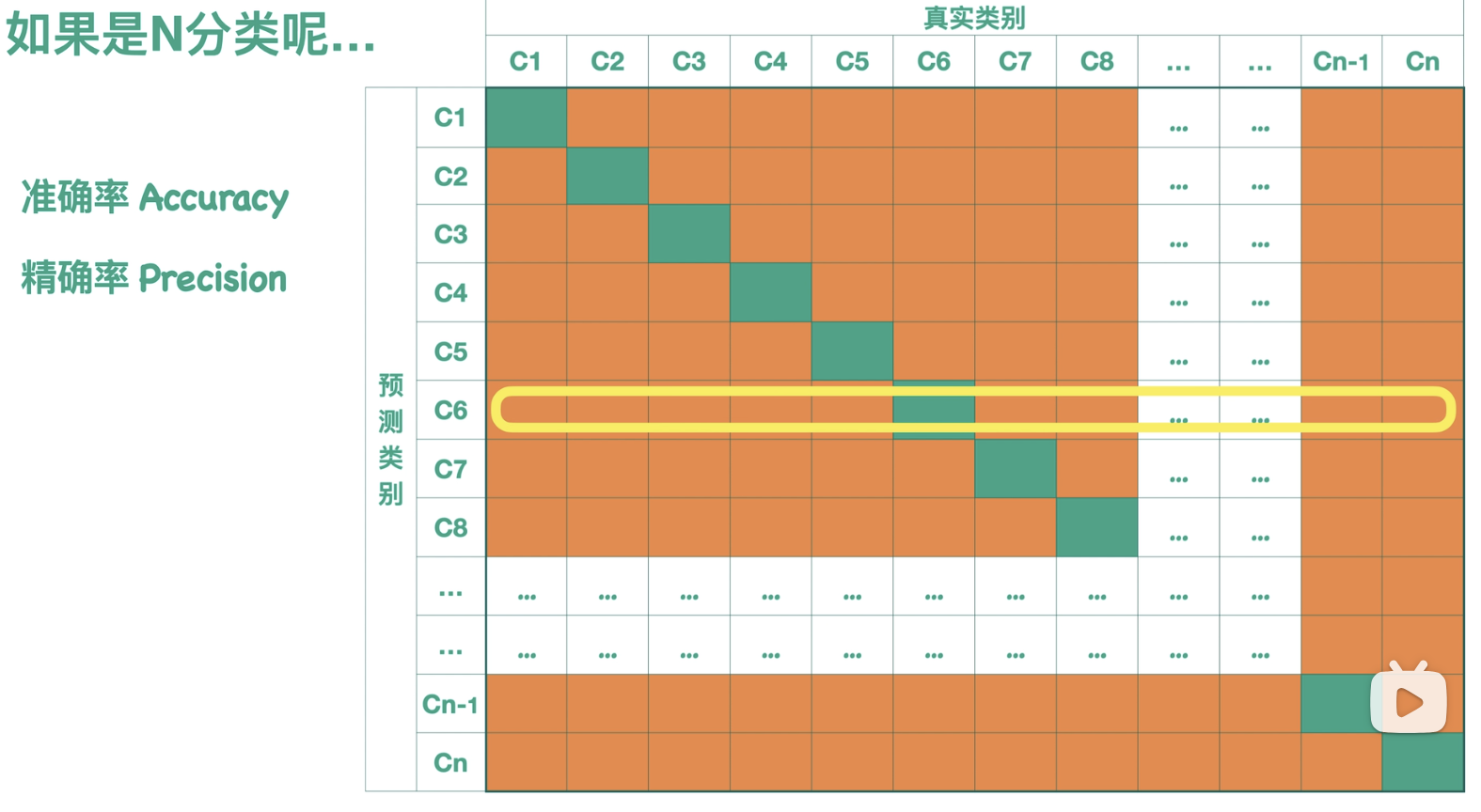
- 召回率(Recall):

- F1:Precision和recall的调和平均。
多分类整体的指标参数的计算:
在多分类问题里,"精确率"和"召回率"默认都是针对某一具体类别计算的;先拿到每个类别的二元指标,再去汇总成全局指标。
从"每类"到"全局"的两种常见聚合:
名称 计算方式 特点 macro-average(平均1) 先算每个类的 Precision/Recall,再算术平均 平等看待小类,易受稀有类影响 micro-average(平均2) 先把所有类的 TP、FP、FN 累加,再算术平均 平等看待每个样本,大类权重高 weighted-average(加权平均) macro 的加权版,权=各类真实样本量 兼顾样本不平衡
二.ROC曲线与AUC值
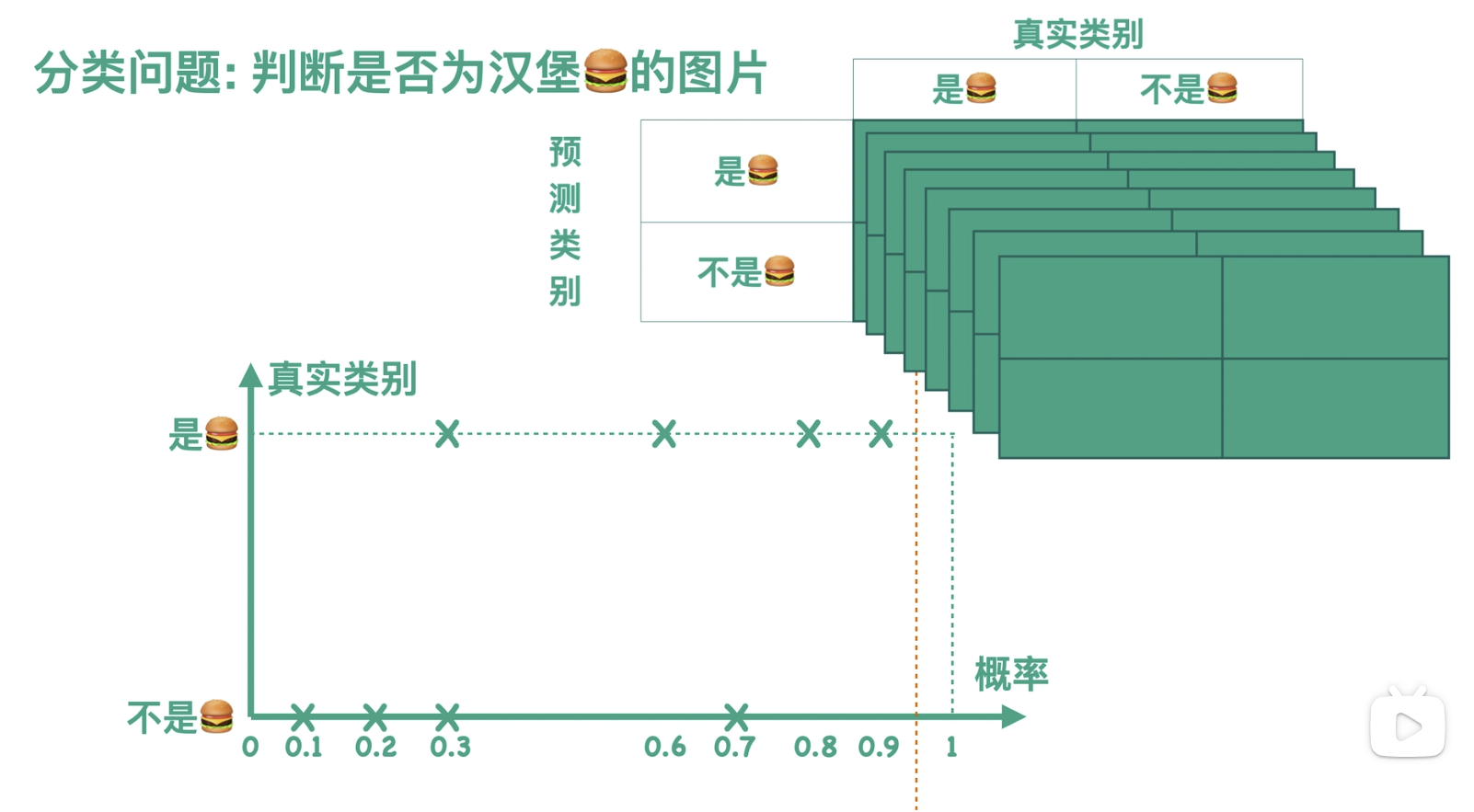
接着之前的例子,假设此时我们有一个分类器,可以判断一张图片是否为汉堡:
实际上,我们的分类器会先计算得到一张图片属于汉堡这一类的概率,进而对图片的类别进行预测:汉堡或者不是汉堡。如果我们用概率来表示横坐标,用真实类别来表示纵坐标,那么分类器在测试集上的效果就可以用图中的散点图来表示: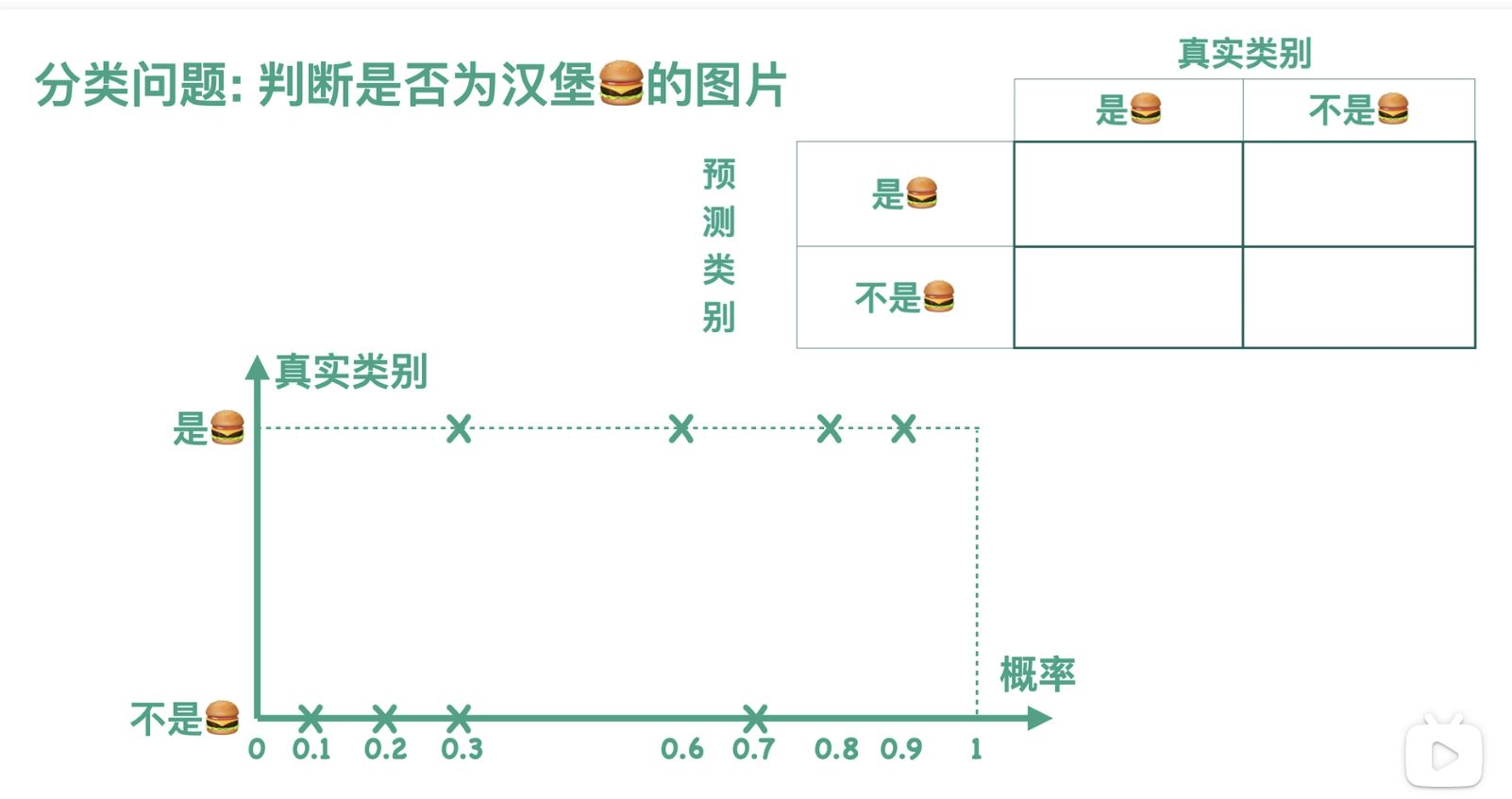
那么怎么样才能够通过概率得到预测的类别呢?
通常我们会设定一个阈值,这里以 0.5 为例,当概率大于等于 0.5 的时候,分类器认为这张图片是汉堡,也就是图中虚线右边的部分,我们用橙色来表示;当概率小于 0.5 的时候,分类器认为这张图片不是汉堡,也就是图中虚线左边的部分,我们用薄荷绿来表示。我们可以根据图中的预测结果得到一个混淆矩阵,例如图中右上角的三个点,一方面它们是橙色的,表示分类器把它们预测成了汉堡,另一方面它们的纵坐标对应于真实类别为汉堡这一类的图片,故而混淆矩阵的右上角方块有三个样本。以此我们可以求得混淆矩阵的其他数值。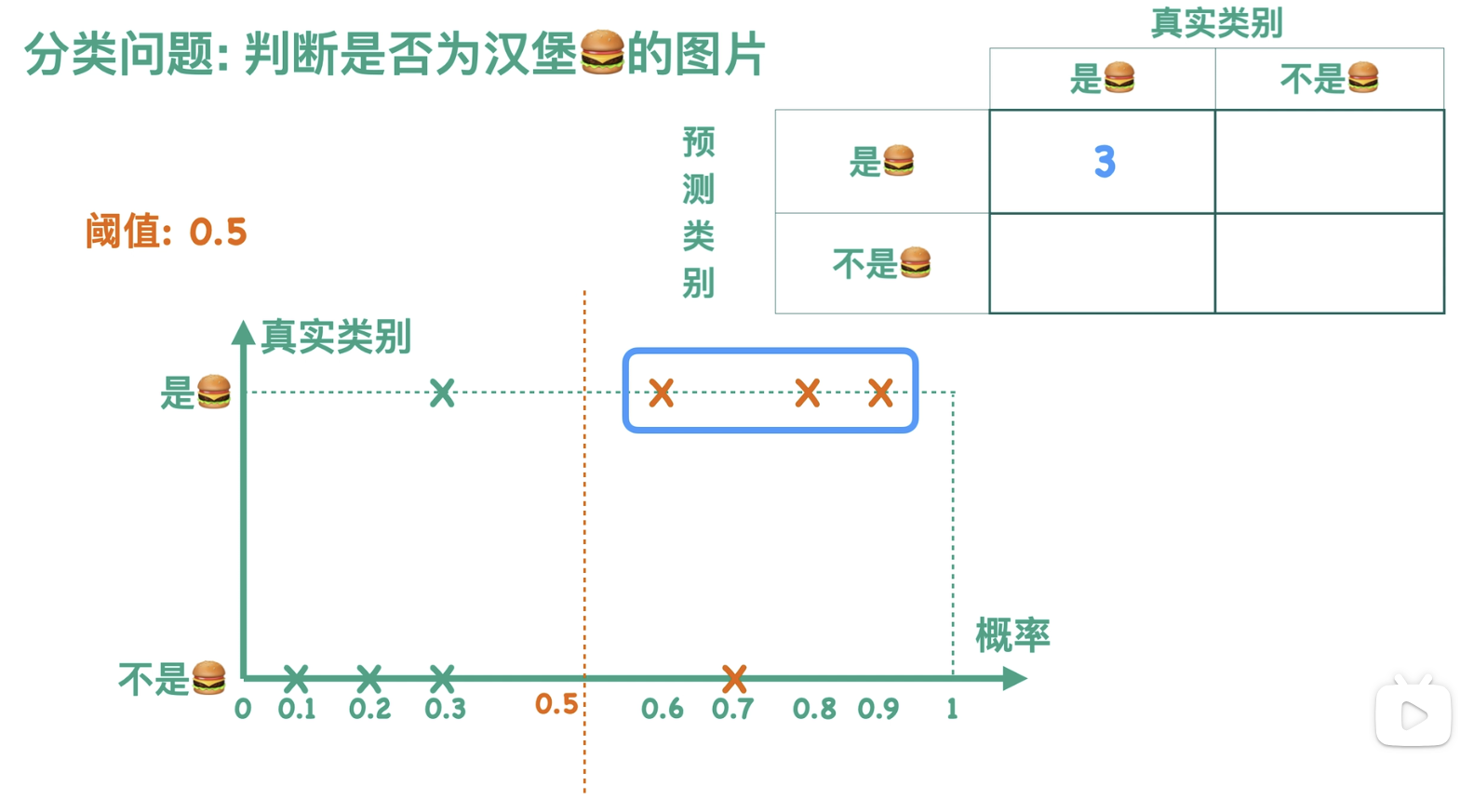
故而当阈值为 0.5 的时候,有且仅有一个混淆矩阵与之对应:
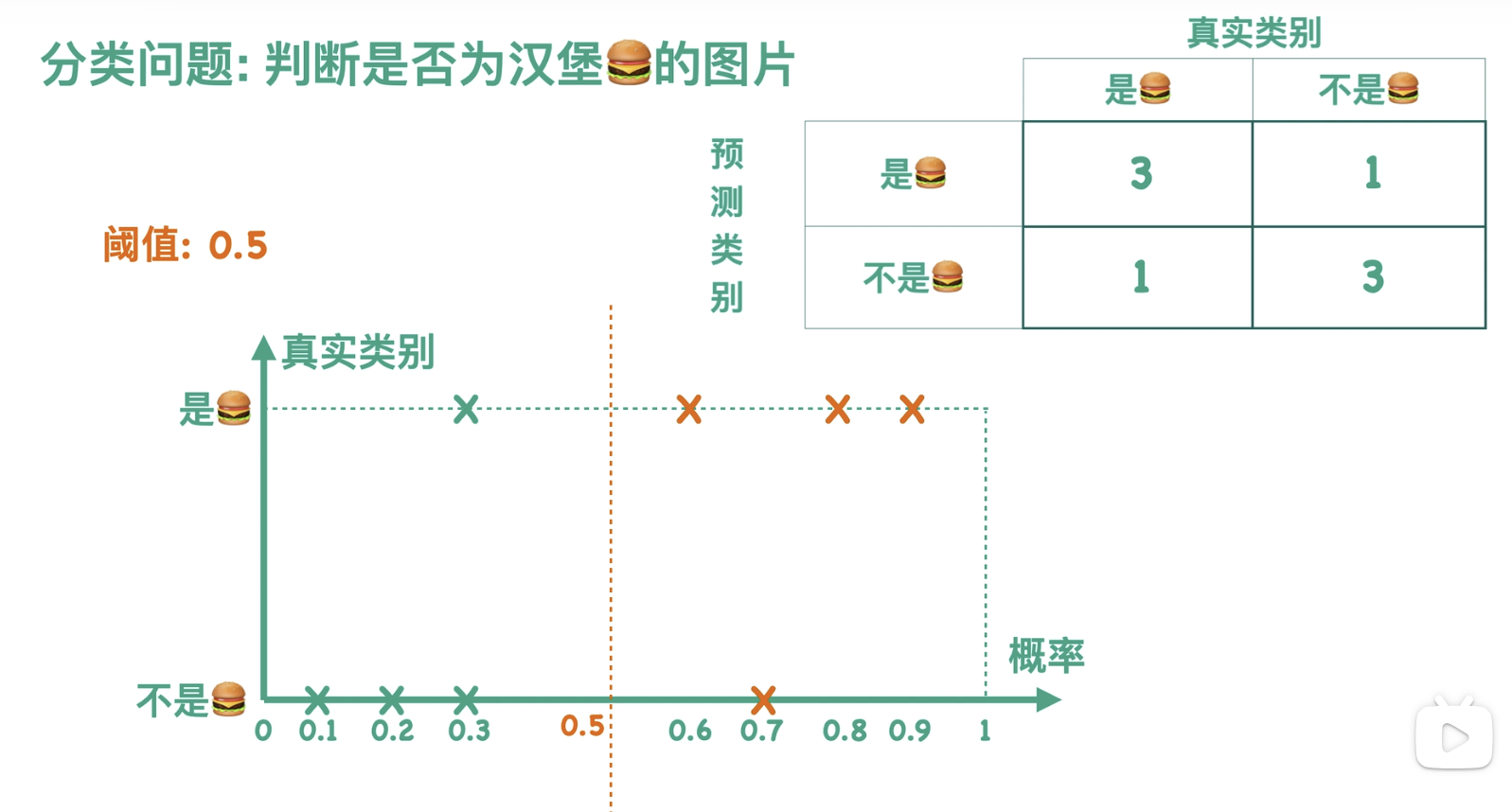
实际上,我们的阈值可以取 0 到 1 之间的任何一个数,所以我们可以得到很多个混淆矩阵。

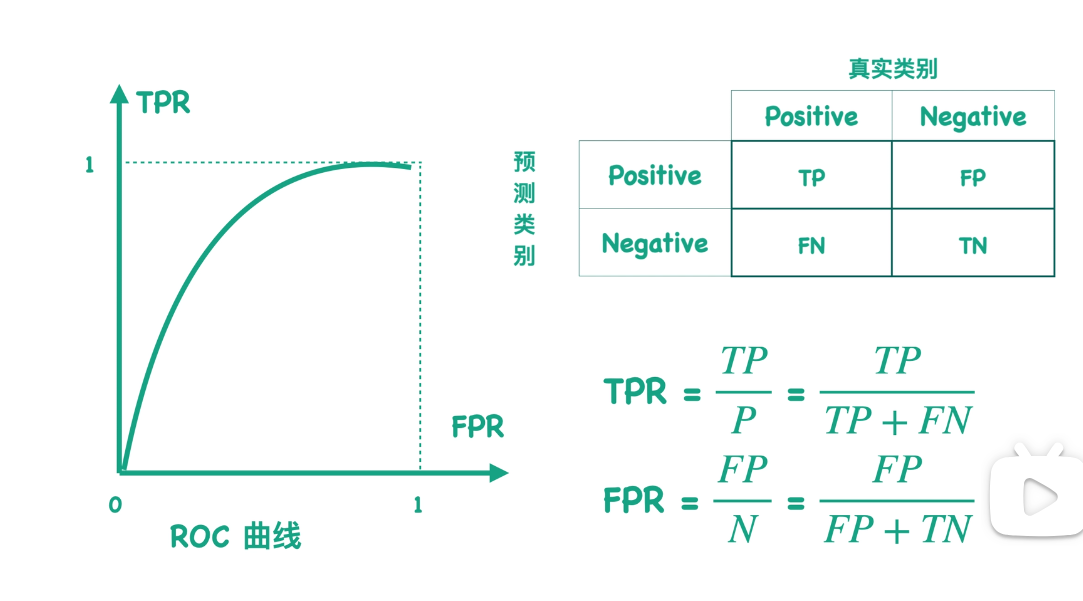
对于一个混淆矩阵,我们可以求出TPR和RPR两个指标:
对于一个混淆矩阵,我们可以求出tpr和fpr两个指标,如果把这个一对数映射到二维空间中,并且让tpr来表示它的横坐标,fpr来表示他的纵坐标的,则平面中的一个点与这个混淆矩阵对应,当我有很多个混淆矩阵的时候,对应的二维空间中就会有很多个点,如果我们把这些点连起来得到的曲线就是我们所说的roc曲线:
回到刚刚那个例子,我们可以求得刚刚那个例子的ROC曲线: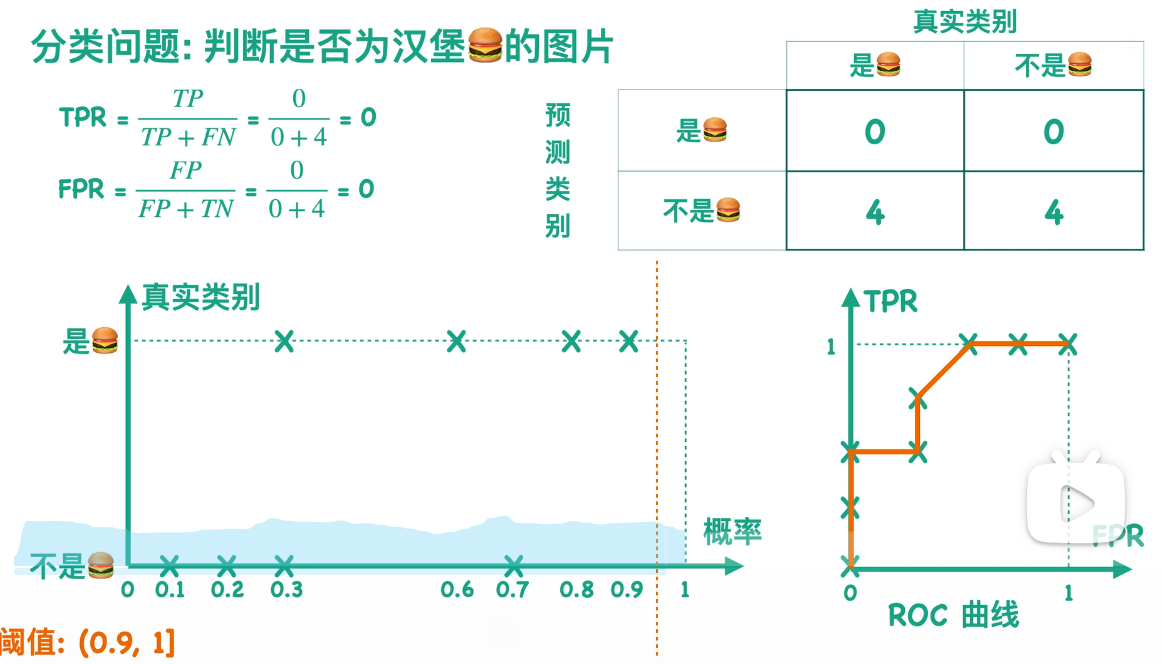
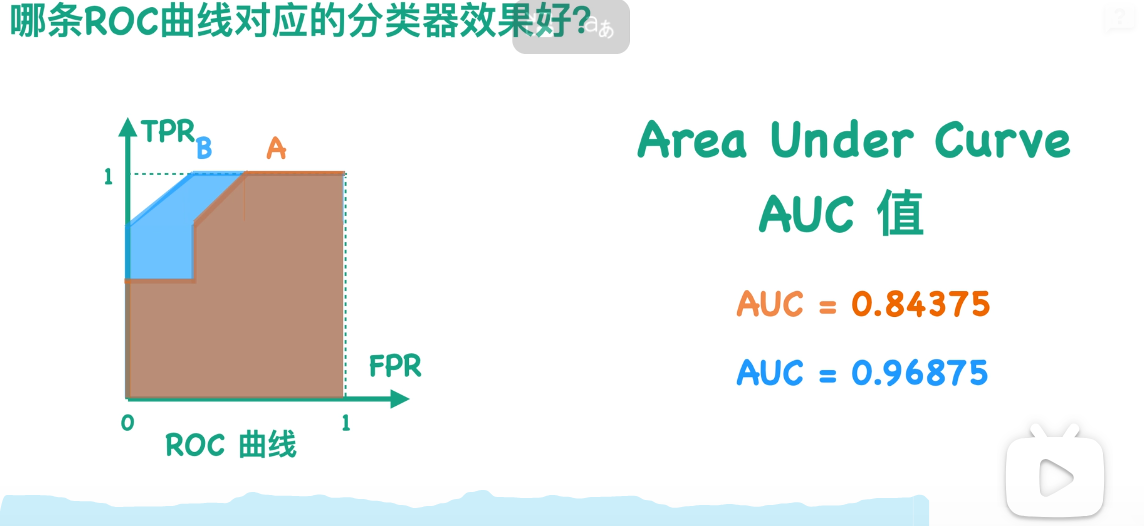
假设我有一个分类器B,它所对应的ROC曲线是蓝色的。那么有没有办法来判断哪个曲线效果更好呢?
让我们来分析下TPR和FPR的公式。显然TPR和FPR的分母对于同一个测试集是固定不变的,因为P和N分别表示测试集中正负样本的数目。所以TPR和FPR仅与TP和FP相关。由于TP表示分对的情况,而FP表示本应属于negative类的样本被分类器错误地分成了positive,所以我们希望TP尽可能大,而FP尽可能小。也就是说,我们想让TPR尽可能大、FPR尽可能小。故而在ROC空间内,曲线越靠近左上角效果越好。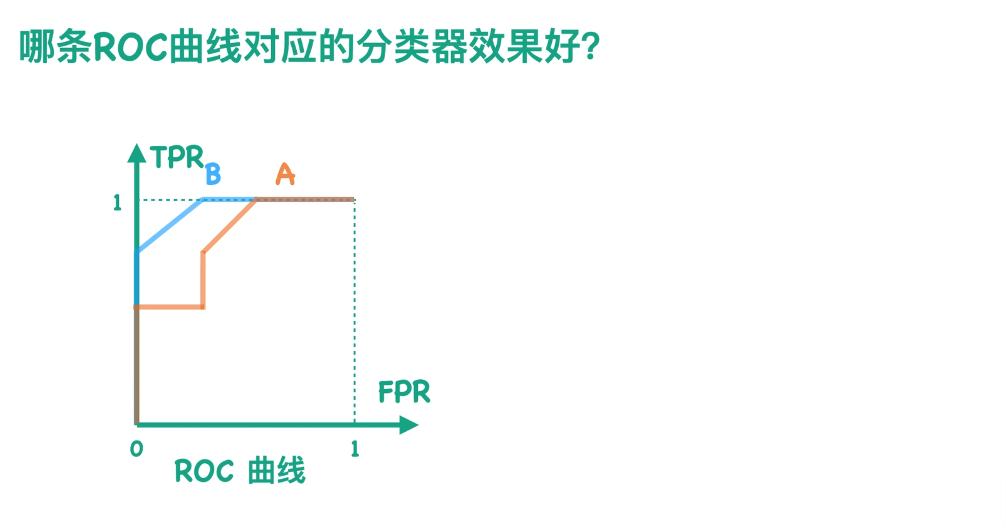
那么我们能不能用一个数值来表示,而不是单纯通过图片来看呢?因为我们通过图片显然能够看到B是比A的效果好的,因为B更靠近左上角。那么我们其实就可以用曲线与坐标轴围成的面积来表示,这就是我们通常所说的AUC值。AUC值的取值范围通常是0到1,并且这个值越大越好。通过计算我们可以知道蓝色的AUC,也就是分类器B要高于分类器A,这也与我们刚才的观察结果相一致。
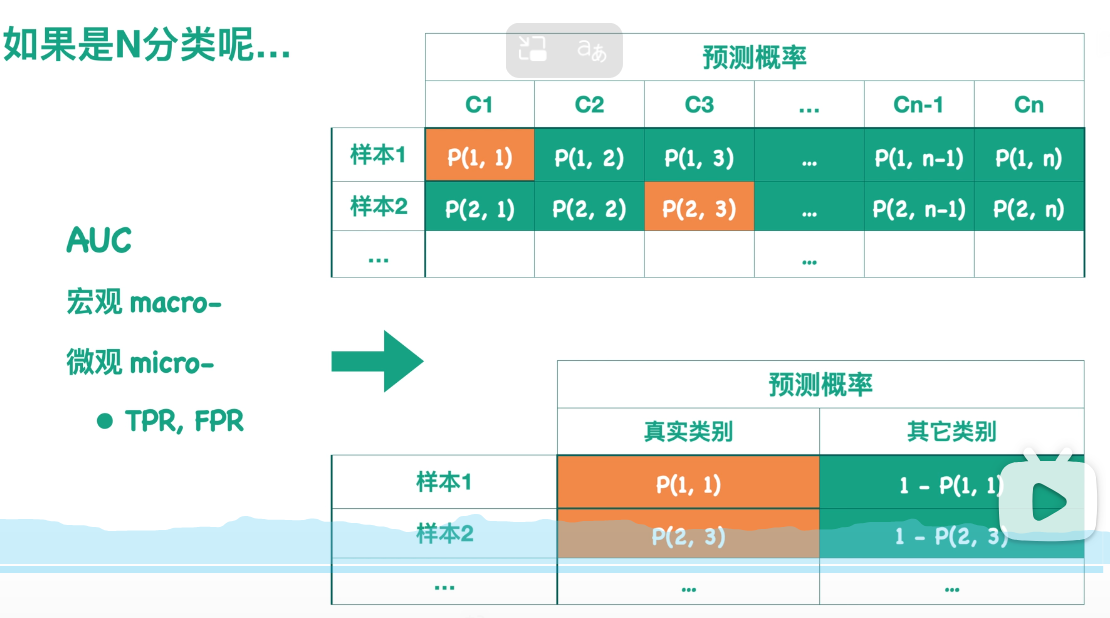
对于多分类问题,怎么样计算AUC呢?
其实它与F1 Score一样,我们可以求得宏观的AUC和微观的AUC。
对于宏观的AUC来说,针对每一个类别,我们都可以画一个ROC曲线,求出对应的AUC值,最后对所有的AUC值求某种平均作为整个模型所有类别的宏观AUC值。
而对于微观的AUC,假设我们的概率预测结果如上表所示。每一行表示一个样本被预测为各个类别的概率:例如第一行表示样本1被预测为C1类的概率为P11,被预测为C2类的概率为P12。橙色的方块表示该样本所属的真实类别(例如样本1真实类别为C1,样本2真实类别为C3),且每行所有的概率和为1。至此,我们可以得到一个经过转化的预测结果,如图。
我们可以根据这个表来得到一个新的、针对整个模型的ROC曲线,以及它对应的AUC值。
三.ROC曲线与PR曲线:
二者关系:
首先,咱们接着上次聊的话题,当我们设置不同的阈值的时候,我们就可以得到不同的混淆矩阵,而每个混淆矩阵又会对应一个TPR值和FPR值。如果我们把所有的这样的TPR值、FPR值映射到一个二维空间中,并且把这些点连起来,我们就可以得到我们所说的ROC曲线。
那么现在如果我们用Precision值来代替之前的TPR值,用Recall值来代替之前的FPR值,并且把这些点连起来得到一条新的曲线,那么这条曲线就是我们通常所说的Precision-Recall曲线,也就是PR曲线。
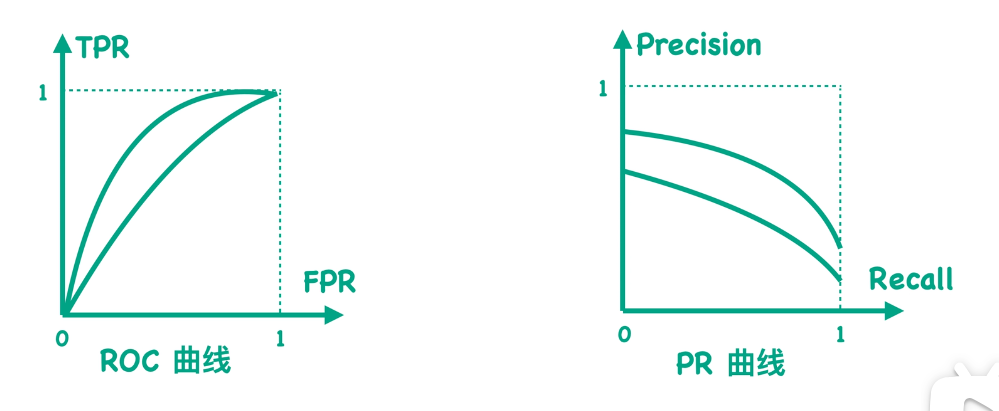
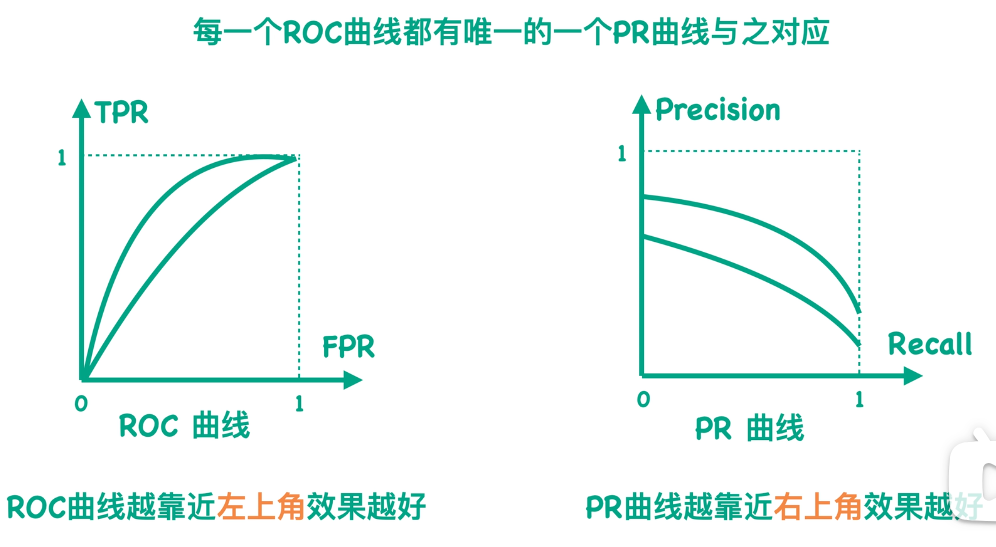
因为对于一个混淆矩阵来说,我们都有唯一的一个TPR值和FPR值的数值对,也可以计算出唯一的一个Precision值和Recall值的数值对。所以我们可以说每一个ROC曲线都有唯一一个PR曲线与之对应,也就是说它们之间是可以相互转化的,并且它们是一一对应的关系。
上一节咱们提到ROC曲线越靠近左上角效果越好。那么对于PR曲线来说,因为我们是希望Precision值和Recall值同时越大越好,所以我们会说它是越靠近右上角效果越好。

既然ROC曲线和PR曲线之间可以相互转换,那我们自然会想到它们之间还有什么别的关系呢?有什么比较重要的关系呢?
我读了一篇论文,它说如果在一个ROC空间中一条曲线dominates另一条曲线,那么在对应的PR空间中,它也一定是dominates另一条曲线的,并且这个结论反之也是成立的。这里它提到dominance这个词------其实我不太会翻译------它有别的意思,就是说如果一条曲线dominates另一条曲线,那么前一条曲线上的所有点一定都是在后一条曲线的上方。
解释 :若曲线A支配 曲线B,则曲线B的所有点都位于曲线A的下方或与之重合 。换句话说,在相同阈值下,曲线A的分类性能在所有位置都严格优于或等于曲线B。
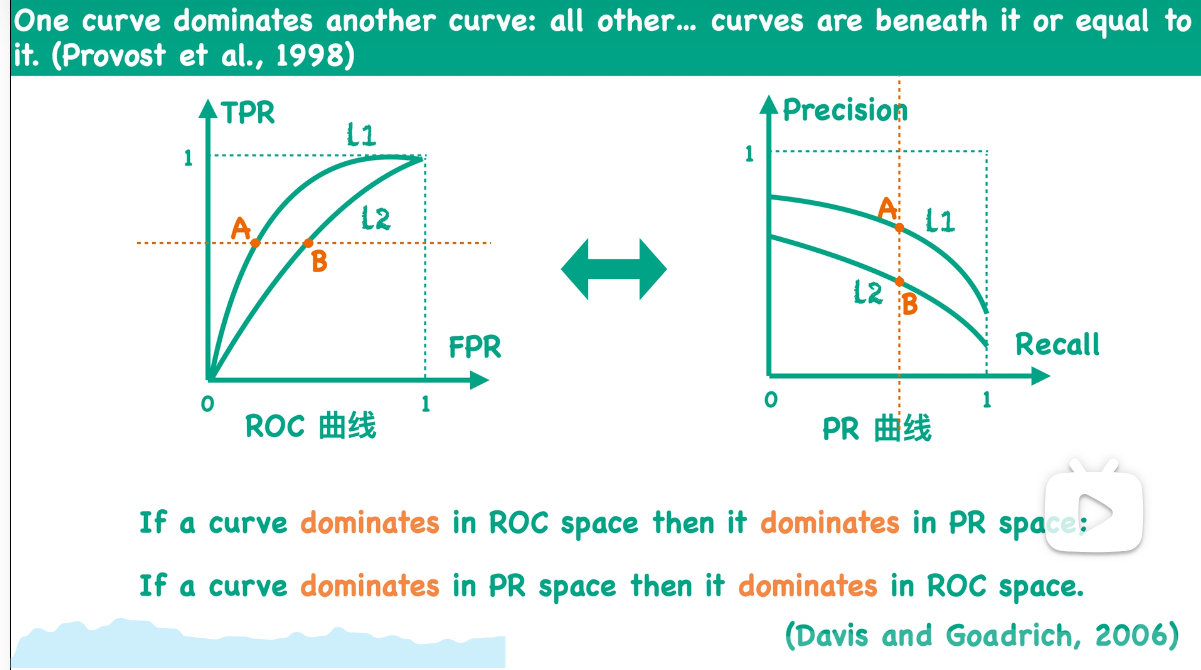
因为a点是在曲线L1上,而b点在曲线L2上,所以我们同样可以看出L1 dominate L2。也就是说,在ROC空间中,如果曲线L1 dominate L2,那么在PR空间中曲线L1也一定dominate L2。
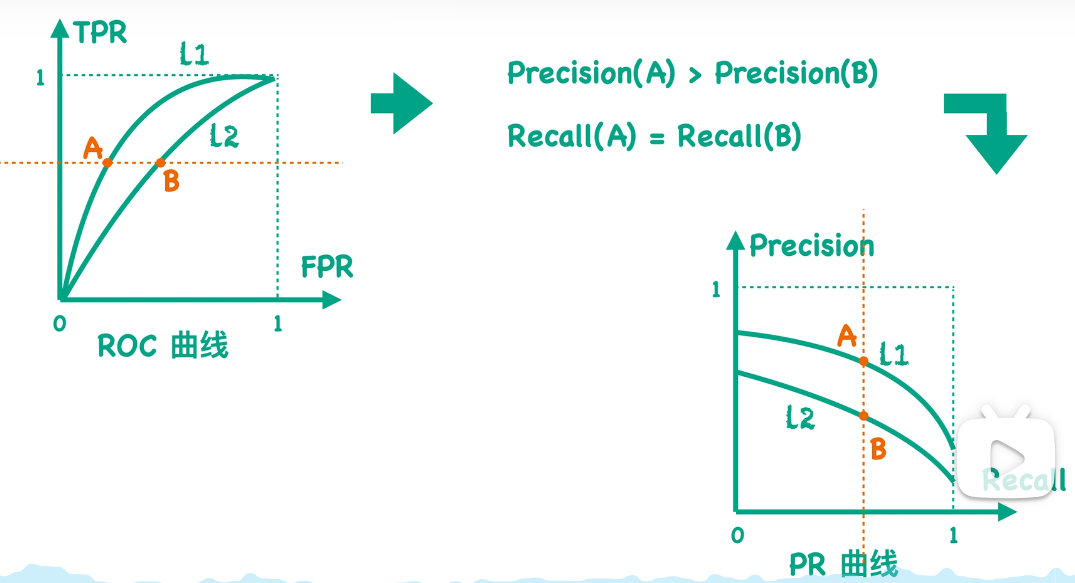
反之也成立:
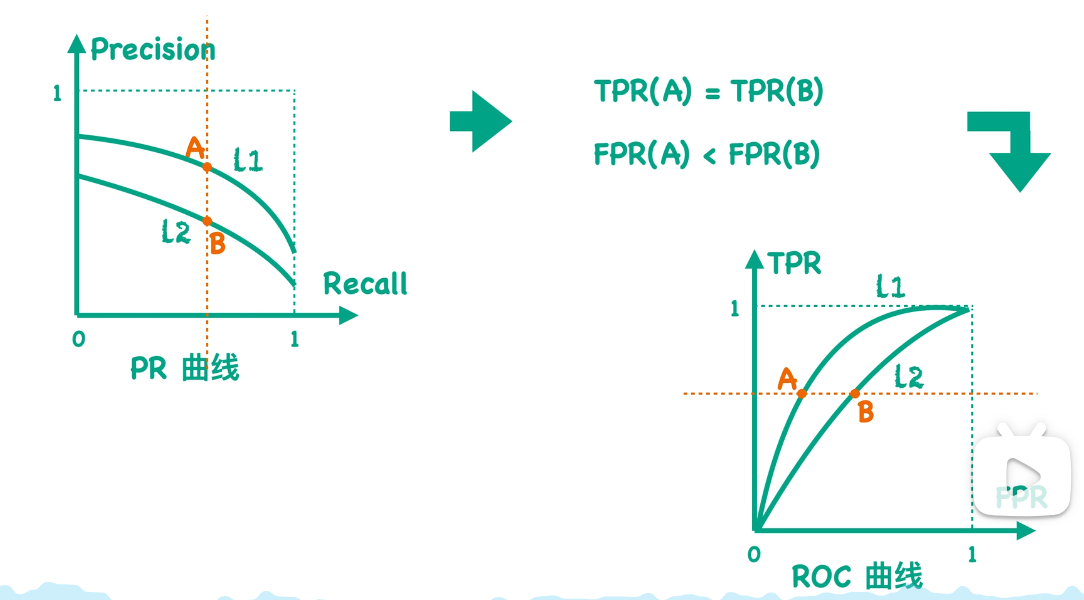
应用场景:
ROC曲线反映的是不同阈值下TPR值和FPR值的关系,而PR曲线反映的则是Precision和Recall的关系。根据定义我们知道TPR值是等于Recall值的,所以这两条曲线最大的区别就是FPR值和Precision值:
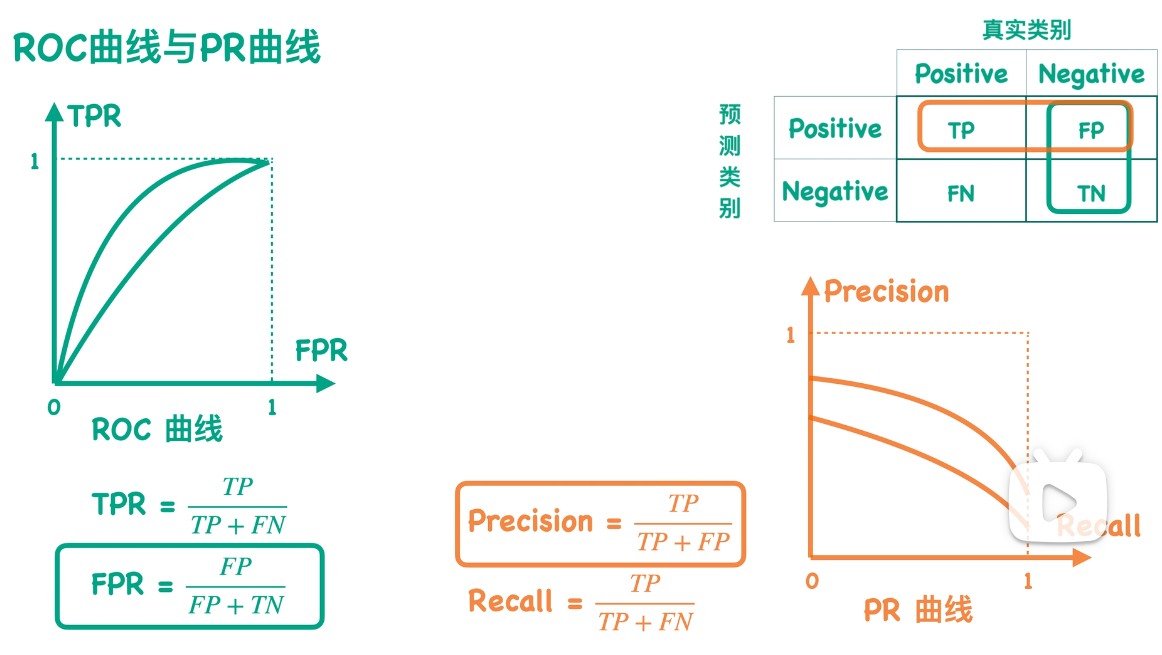
根据公式我们知道,FPR值反映的是FP值和测试集样本中所有负类样本总数的比例,而Precision反映的是TP值和预测得到的positive类别总数的一个比例。
下面我们来看一个例子:
假设对于同一个测试集,我有两个分类器A和B。这两个分类器得到的TP值和FN值都相同,它们的区别就是得到的FP值不同。假设分类器A的FP值等于10倍的TP,而分类器B的FP值等于100倍的TP,并且它们的FP值都远远小于负类样本总数。那么代入公式就可以知道TPR值和Recall值对于这两个分类器是一样的,因为它们只和TP值及FN值相关。
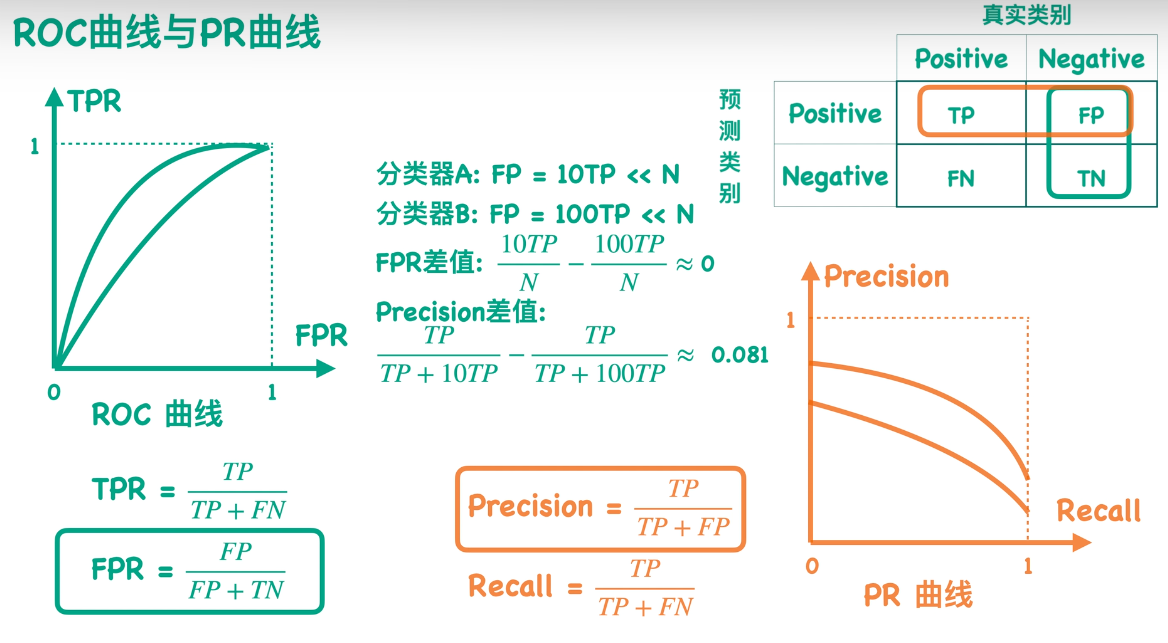
所以我们可以得出一个结论:对于ROC曲线来说,它对正负两类是同等的关注;而对于PR曲线,它对正类更加关注,因此更能够反映出这样的两个分类器的差异。
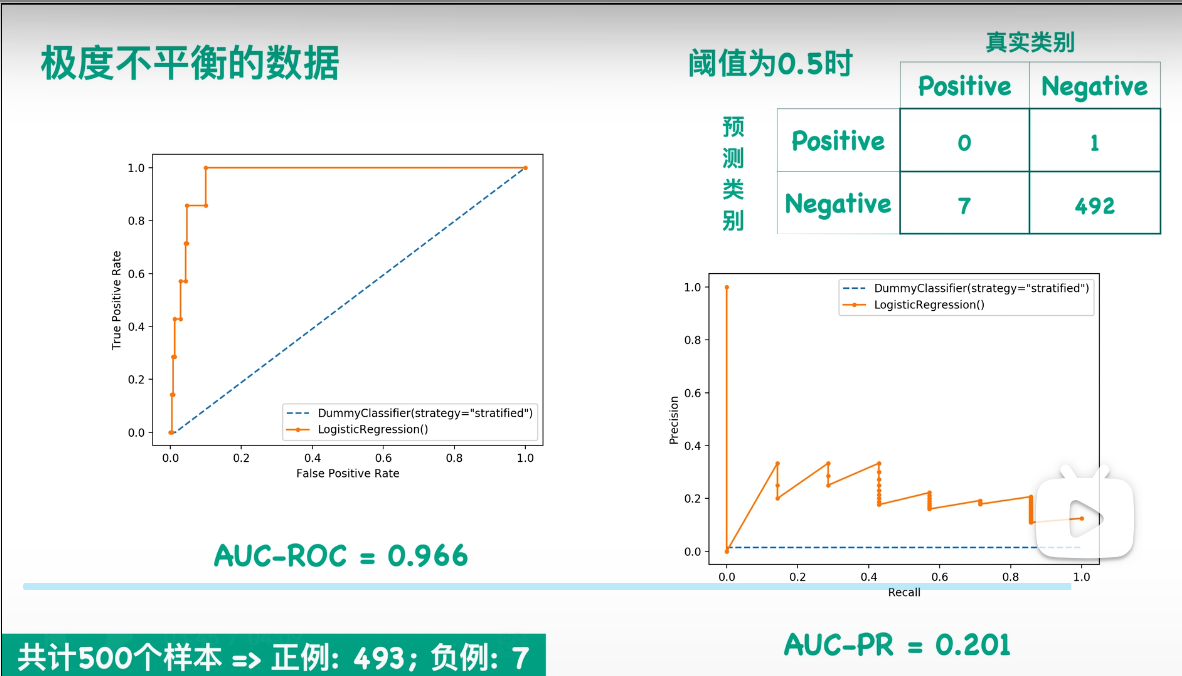
下面我们来更直观地举一个例子。假设我有500个样本,然后这个数据也是极度不平衡的数据。如果我们画出它的ROC曲线,就可以得到左边这个图;而如果我们画出它的PR曲线,就可以得到右边这个图。你们可以很明显地看出,右边这个图效果是很差的,而左边这张图看起来模型效果很好。我们来看一下当阈值为0.5的情况。我画了一个相应的混淆矩阵:也就是说,当我的模型是逻辑回归时,如果设置阈值为0.5,我可以得到右上角这样的一个混淆矩阵。我可以发现它对正类一个都没预测对。尽管是在这么差的情况下,但是我左边的ROC曲线看上去分类器效果仍然非常好,因为我的负类实在是太多了。而右边的PR曲线却能够反映出我这个模型效果不太好,所以在这种情况下需要选用PR曲线。