你好,支持向量机!------ 给初学者的"分类大师"入门指南
写给第一次听说的你: 别被"支持向量机"这个名字吓到。如何在混乱的世界里,画出一条最完美的"分界线"。
开篇:生活里的"分界线"无处不在
想象一下,你正在整理一本厚重的相册。
- 有一堆苹果的照片,和一堆橘子的照片,它们混在一起。
- 你的任务很简单:把苹果和橘子分开,放进两个不同的盒子里。
你会怎么做?
你可能会仔细观察:苹果通常更红、形状更圆润;橘子偏橙色、表皮有颗粒感。 然后,你在大脑里模糊地画出一条"分界标准":颜色偏红且光滑的放左边,颜色偏橙且有纹理的放右边。
这个"画分界标准"的过程,就是"分类"。 而支持向量机(Support Vector Machine,简称SVM) ,就是计算机世界里一位极其严谨、力求完美的"分类大师"。它最擅长做的事情,就是在各种复杂的数据中,找到那条最优、最稳健的"分界线",将不同类别的事物清清楚楚地区分开。
在人工智能的早期,SVM曾是最闪耀的明星之一,尤其在图像识别、文本分类等领域立下了汗马功劳。今天,就让我们抛开畏惧,一起认识这位逻辑清晰、追求极致的"分类大师"。
一、 分类归属:SVM在AI家族中的"户口本"
在开始了解SVM怎么工作之前,我们先给它上个"户口",看看它在庞大的AI家族里,属于哪一支。
首先,需要澄清一个常见的误解:支持向量机(SVM)并不是一种"神经网络" 。它们是人工智能中两种非常重要但不同的模型流派。
你可以这样理解:
- 神经网络:模仿人脑神经元连接,像一个庞大的、可自我调整的"网状电路",通过层层传递和变换信息来学习。
- 支持向量机:基于严格的数学和几何原理,像一个追求极致完美的"建筑师",目标是在数据空间中构建一个最优的"隔离结构"(比如一堵墙、一个平面)。
如果非要从你要求的几个维度来给SVM定位:
- 按网络结构拓扑 :不属于任何神经网络结构。它没有"层"和"神经元"的概念。
- 按功能用途 :核心是分类 (当然经过扩展也能做回归等其他任务)。它是监督学习的代表性算法,意味着我们需要先给它看大量"带标签"的数据(比如标明是苹果还是橘子的照片)它才能学习。
- 按核心思想 :属于最大间隔分类器。这是它最独特的标签,也是其强大和优雅所在。它的目标不是随便画一条线分开数据,而是要找那条让两个类别"间隔"最大的线,从而获得最强的泛化能力(对没见过的数据也分得好)。
简单总结:SVM是机器学习"监督学习"门派中的一位"几何学派"高手,专精于寻找最优分类边界,与"连接主义学派"的神经网络各有千秋。
二、 底层原理:SVM的"完美主义"分界艺术
现在,让我们走进SVM的内心世界,看看这位"分类大师"到底是如何思考和工作的。
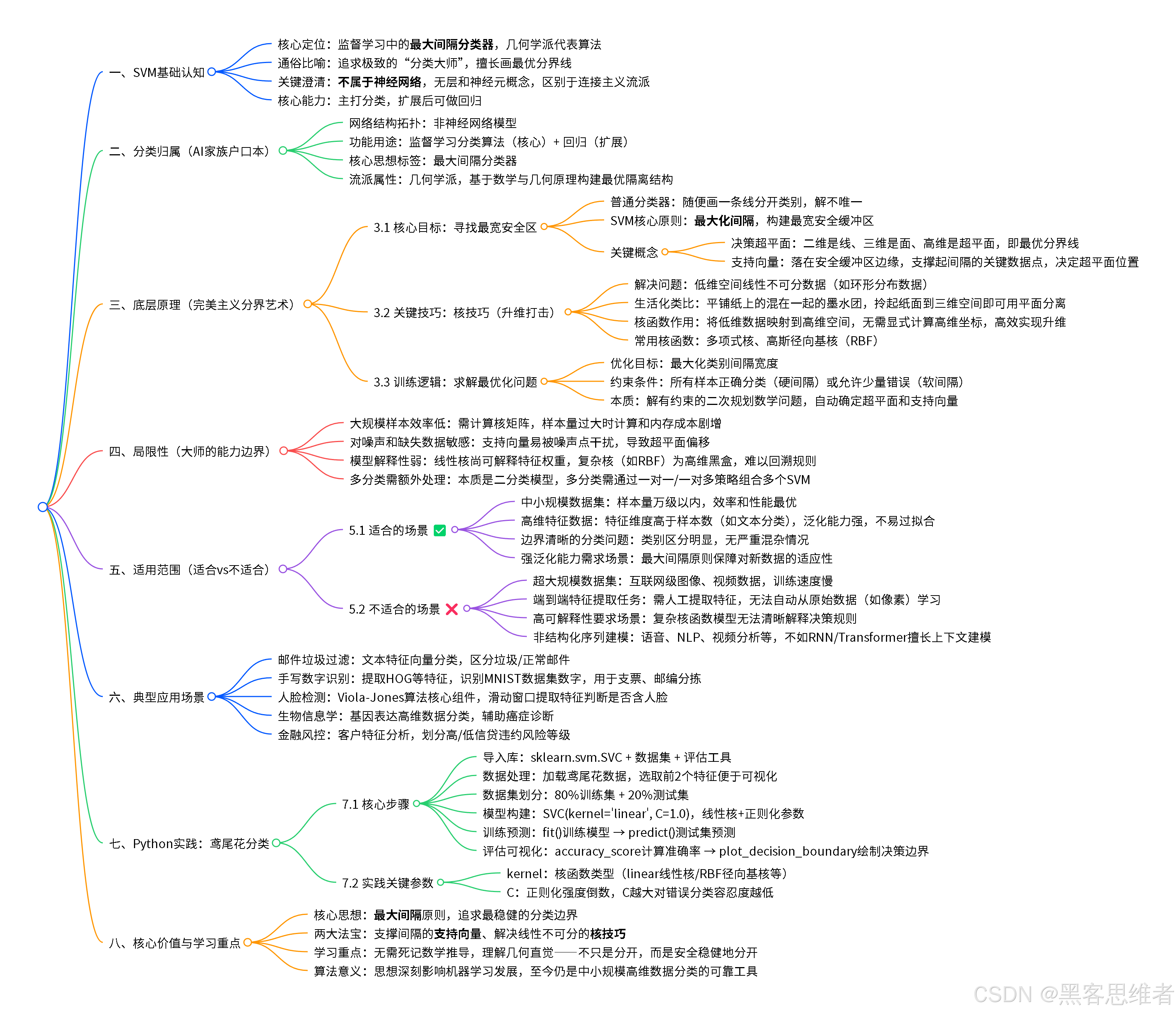
1. 核心目标:寻找"最宽的安全区"
让我们回到苹果和橘子的例子。假设现在我们只用两个特征来衡量它们:颜色红度(X轴) 和表皮光滑度(Y轴)。每个水果在这张图上就是一个点。
普通分类思路:只要找一条线,能把苹果点(红色)和橘子点(橙色)大致分开就行。这样的线可能有无数条(如图中灰色线所示)。
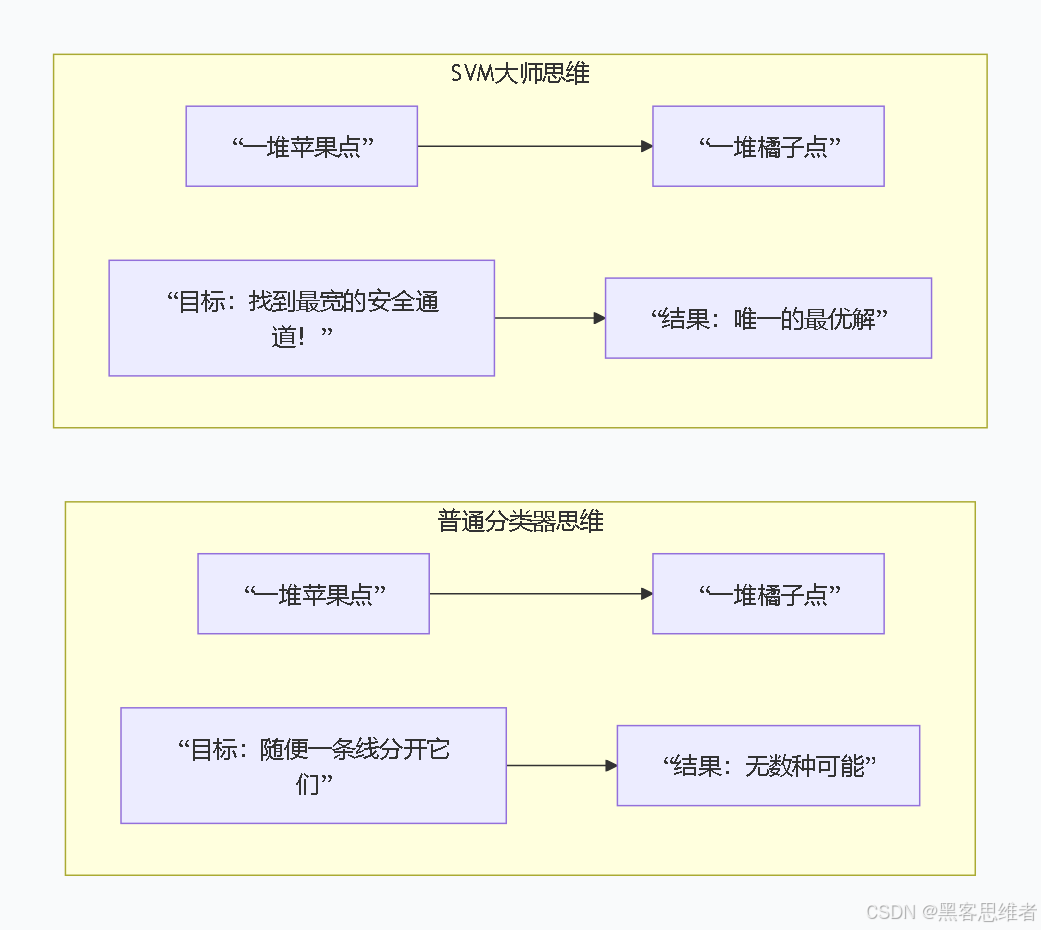
SVM的完美主义思路:
"不,这些线都太冒险了!它们离两边的点都太近。万一来了一个长得稍微特别点的苹果(比如青苹果),或者一个特别光滑的橘子,就很容易被分错。我要找的,是一条能让两个类别'隔得最开'的线。在这条线的两侧,我要留出尽可能宽的'安全缓冲区'(我们称之为'间隔')。这样,即使新来的数据点有些许偏差,也能被正确分类。"
这条"最优分界线" ,SVM称之为 "决策超平面" (在二维是线,三维是面,更高维叫超平面)。
那些落在'安全缓冲区'边缘、支撑起这个缓冲区的关键数据点 ,就被称为 "支持向量" 。这就是"支持向量机"名字的由来------由关键向量(点)支撑起的机器。
2. 关键技巧:当一条线不够用------"升维打击"
现实往往更复杂。如果苹果和橘子这样分布呢?它们像两个交织在一起的圆圈,在二维平面上,你用一根直线无论如何也画不出完美的分界线。
橘子点: (⊙) 形成一个圈
苹果点: (◎) 在橘子圈外面形成另一个圈(在二维平面上,这两类点呈环形分布,直线无法分离)
这时,SMP展现出了它最精妙的一招:核技巧(Kernel Trick)。
生活化类比 :想象你在一张平铺的纸上,画了两个混在一起的墨水团,无法用一根直线分开。现在,你轻轻拎起纸的中心,墨水团随着纸面被提起到三维空间。在三维空间里,你可能发现用一个平面就能轻松地把两个墨水团分开了!这个"把纸拎起来"的操作,就是"升维映射"。核技巧就是完成这个神奇映射的数学工具,而且计算非常高效。
对于SVM来说 :它通过一个巧妙的数学函数(核函数),将原始数据从难以分割的低维空间,"投射"到一个更容易找到"决策超平面"的高维空间,然后在高维空间里执行它最擅长的"找最大间隔平面"的任务。常用的核函数有"多项式核"、"高斯径向基核(RBF)"等,它们定义了不同的"投射"方式。
3. 训练的核心逻辑:解一道最优化数学题
SVM"学习"的过程,本质上是在解一道有约束条件的数学最优化问题:
- 目标(Objective):最大化"间隔"(安全区的宽度)。
- 约束(Constraints):确保所有训练数据点都被正确分类(或允许少量错误,即"软间隔"),并且分到正确的一侧。
通过求解这个问题,SVM就能自动找到那条最优分界线(决策超平面)的位置,以及确定哪些数据点是至关重要的"支持向量"。
三、 局限性:大师也不是万能的
了解了SVM的强大,我们也要客观地认识它的边界。理解了局限,才能更好地使用它。
-
对大规模训练样本效率较低:SVM的训练过程本质上要解一个二次规划问题,当样本量非常大(例如数十万、百万)时,计算时间和内存消耗会显著增加。相比之下,一些神经网络模型(如使用随机梯度下降)对海量数据的处理更具扩展性。
- 为什么? 因为它需要计算所有样本点之间的关系(核矩阵),样本越多,这个矩阵就越大,计算越慢。
-
对缺失数据和噪声比较敏感:SVM追求的是"完美"或"近似完美"的分界。如果数据中有很多错误标签(噪声)或特征缺失严重,会直接影响支持向量的位置,导致找到的"最优"分界面可能并不理想。
- 为什么? 因为支持向量是决定分界面的"关键先生",噪声点如果恰好成了支持向量,就会"带歪"整个模型。
-
模型解释性相对较弱(尤其在使用复杂核函数时):当使用线性核时,我们可以清楚地理解每个特征的权重(重要性)。但如果使用了像RBF这样的复杂核函数进行"升维打击"后,我们得到的是一个在高维空间中的分界面,很难再回溯到原始特征,向人直观地解释"模型到底是根据什么规则做的判断"。
- 为什么? 我们只知道经过"魔法投射"后数据能分开,但"魔法"的具体变换过程对人类来说是个黑盒。
-
在多分类问题上需要额外处理:SVM本质上是二分类大师。当遇到苹果、橘子、香蕉三个类别时,我们需要通过"一对一"或"一对多"等策略组合多个SVM来解决,这增加了复杂度和训练成本。
四、 使用范围:什么时候该请这位大师出马?
基于以上特点,我们可以为SVM划出清晰的"能力圈":
✅ 适合用它解决的问题(核心优势场景):
- 中小规模数据集:样本量在万级以内时,SVM往往能发挥出极高的效率和性能。
- 高维特征数据:特别是特征维度(成百上千)甚至高于样本数的情况。例如文本分类(每个词都是一个特征),SVM表现非常出色。这在神经网络容易过拟合的场景下是巨大优势。
- 边界清晰的分类问题:类别之间的区别相对明显,不是那种极度混杂、你中有我我中有你的情况。SVM擅长找到清晰的几何边界。
- 寻求强泛化能力的场景:由于"最大间隔"原则,SVM找到的模型通常泛化能力(处理新数据的能力)很强,不容易过拟合。
❌ 不适合用它解决的问题:
- 超大规模数据集(如互联网级别的图像、视频数据):训练会非常慢,内存可能吃不消。
- 需要端到端学习或特征自动提取的任务:例如原始图像识别,CNN可以自动从像素中学习边缘、纹理等特征;而SVM通常需要我们先人工提取好特征(如颜色直方图、SIFT特征等)再喂给它。它不擅长自己"创造"特征。
- 对模型可解释性要求极高的场景:如果法律或业务要求必须解释每一个预测的原因,线性核SVM尚可,但复杂核函数的SVM可能不是最佳选择。
- 非结构化数据序列建模:如语音识别、自然语言理解(需考虑上下文顺序)、视频分析等,这类任务需要模型能理解序列前后的关系,循环神经网络(RNN)或Transformer架构更为适合。
五、 应用场景:SVM在生活中的高光时刻
尽管深度学习如今风光无限,SVM在诸多领域依然是可靠的选择,甚至是首选。
-
邮件垃圾过滤(文本分类)
- 作用:这是SVM的经典应用。系统将每一封邮件转换成一串数字(特征向量),比如哪些关键词出现了、出现的频率等。SVM通过学习大量已标记的"垃圾邮件"和"正常邮件",找到一个最优的超平面,未来新邮件来时,根据它落在超平面的哪一侧,自动判断是扔进垃圾箱还是收件箱。
-
手写数字识别(图像分类)
- 作用:在深度学习兴起前,SVM是MNIST手写数字数据集上表现最好的算法之一。首先,图像被预处理并提取特征(如方向梯度直方图HOG)。然后,SVM根据这些特征,学习区分"0"到"9"这十个数字的决策边界。它的高精度和高效性使其曾被广泛应用于银行支票识别、邮政编码自动分拣等系统。
-
人脸检测(目标检测)
- 作用:在早期的人脸检测算法(如Viola-Jones)中,SVM是核心组件。算法会在图像的不同位置和尺度滑动一个"小窗口",并从每个窗口中提取特征。SVM的任务就是判断这个窗口里的图像特征,是否符合"人脸"这个类别的特征模式,从而快速定位出图像中所有人脸的位置。
-
生物信息学(基因/蛋白质分类)
- 作用:在癌症诊断中,研究人员通过基因芯片获得病人成千上万个基因的表达数据。每个病人就是一个高维数据点(维度即基因数量)。SVM可以学习健康人和病人样本在这些基因表达空间中的差异,找到一个分类模型,用于辅助诊断新病人的样本属于哪一类。它对高维小样本数据的处理能力在这里大放异彩。
-
金融风控(信用评分)
- 作用:银行根据客户的年龄、收入、职业、历史信贷记录等数十个特征,评估其贷款违约风险。SVM可以综合分析这些特征,将客户分为"高风险"和"低风险"两类,为信贷审批提供数据驱动的决策支持,其强大的泛化能力有助于应对各种未知的欺诈模式。
六、 动手实践:用Python和SVM给鸢尾花分个类
理论说了这么多,我们写几行简单的代码,亲眼看看SVM是如何工作的。我们将使用经典的鸢尾花数据集,用SVM根据花瓣和萼片的尺寸来分类三种鸢尾花。
python
# 1. 导入必要的工具库
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC # SVC就是用于分类的SVM
from sklearn.metrics import accuracy_score, classification_report
import numpy as np
# 2. 加载数据:鸢尾花数据集(包含150朵花的4个特征和3个种类)
iris = datasets.load_iris()
X = iris.data[:, :2] # 为了可视化方便,我们只取前两个特征(萼片长度和宽度)
y = iris.target # 标签(0: Setosa, 1: Versicolour, 2: Virginica)
# 3. 划分训练集和测试集(80%训练,20%测试)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 4. 创建SVM分类器模型,这里使用线性核
# C是正则化参数,控制对错误分类的容忍度。C越大,越追求完美分类,可能过拟合。
model = SVC(kernel='linear', C=1.0, random_state=42)
# 5. 训练模型!(这就是SVM在"学习"分界线的过程)
model.fit(X_train, y_train)
# 6. 用训练好的模型在测试集上进行预测
y_pred = model.predict(X_test)
# 7. 评估模型表现
print("测试集准确率:", accuracy_score(y_test, y_pred))
print("\n详细分类报告:")
print(classification_report(y_test, y_pred, target_names=iris.target_names))
# 8. 可视化决策边界 (只针对我们选取的两个特征)
def plot_decision_boundary(model, X, y):
# 创建网格点
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
np.arange(y_min, y_max, 0.02))
# 预测整个网格点的类别
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# 绘制等高线(决策边界)
plt.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.coolwarm)
# 绘制原始数据点
scatter = plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', cmap=plt.cm.coolwarm)
plt.xlabel(iris.feature_names[0])
plt.ylabel(iris.feature_names[1])
plt.title('SVM线性分类器在鸢尾花数据集上的决策边界')
plt.legend(handles=scatter.legend_elements()[0], labels=iris.target_names.tolist())
plt.show()
# 绘制决策边界(在训练集上)
plot_decision_boundary(model, X_train, y_train)运行这段代码,你会看到:
- 控制台打印出模型在测试集上的准确率(通常很高)。
- 弹出一张图,图上用不同颜色区域清晰地展示了SVM学习到的三条决策边界(因为是三分类),将三种鸢尾花的数据点分开。那些位于颜色区域交界处的点,很可能就是"支持向量"。
通过这个简单的例子,你就能直观地感受到SVM作为"分类大师"的魅力所在。
总结
支持向量机(SVM)的核心价值在于:它用一种优雅且坚实的几何与最优化思想,在数据中寻找那个最稳健、最普适的"真理边界"。
对于初学者而言,理解SVM的重点不是记忆复杂的数学推导,而是把握住它的核心思想 :"最大间隔"原则 ,以及它的两大法宝 :处理线性不可分数据的"核技巧" 和决定分界面的"支持向量"。
它或许不再是当下最热门的模型,但它的思想深刻影响了机器学习的发展。学习SVM,不仅能掌握一个至今仍在许多场景下高效可靠的强大工具,更能帮助你建立起对"什么是好的分类模型"的深刻直觉------追求的不只是分开,而是以最从容、最安全的方式分开。
这位严谨的"几何学派"大师,永远是你在探索人工智能道路上,值得尊敬与信赖的伙伴。