计算机组成原理（8）：各种码的作用详解

引言

在计算机科学的浩瀚海洋中，了解数据如何被编码、存储和处理是每一个开发者的基本功。

在上一篇文章中，我们初步介绍了定点数的编码表示，里面提及到了四大码的基本概念。

今天，我们将继续深入探讨计算机底层中最基础也是最核心的概念之一------数值表示法中的原码、反码、补码以及移码，如果对四种码的知识点已经熟能生巧的同学可以不用看。

这些概念看似简单，实则蕴含着深刻的数学原理与设计哲学。通过这篇文章，你将不仅掌握它们的基础知识，还能理解其背后的逻辑，并学会如何在实际编程中应用这些知识。

一、原码：直观但计算复杂

让我们从一个具体的例子开始，深入探讨各种编码方式的缺陷和作用。

假设我们有一台8位字长的计算机，有两串二进制数据：

复制代码

00001110  (14)
11110010  (-14)

如果这两个二进制数表示的是无符号数 ，它们的值分别是14和242（11110010 = 242），相加结果是256，即1 0000 0000，高位进位被丢弃后，结果是0。但14+242=256，256模256=0，这与结果一致。

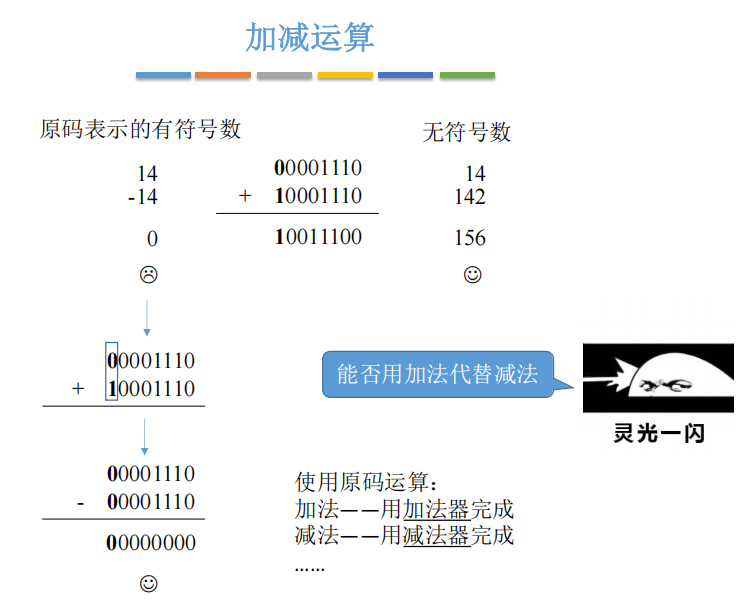
问题来了 ：如果这两个数表示的是有符号数（原码表示），那么：

上面的数：符号位为0（正数），尾数1110=14 → +14
下面的数：符号位为1（负数），尾数1110=14 → -14

那么+14 + (-14) 应该等于0，但按照简单的二进制加法规则：

复制代码

  00001110  (+14)
+ 11110010  (-14)
------------
 100000000  (256)

高位进位1被丢弃，结果是00000000（0），看起来是正确的？但等一下，这个结果是巧合吗？

让我们再看一个例子：+14 + (-15)

复制代码

  00001110  (+14)
+ 11110001  (-15)
------------
 100000000  (256)

结果也是00000000（0），但+14 + (-15) = -1，不是0！

原码的致命缺陷：在上文也提到过，当符号位不同时，原码的加法运算无法正确得到结果，必须先判断符号，再进行相应的加减操作。这意味着ALU（算术逻辑单元）需要设计专门的减法电路，增加了硬件复杂度。

原码的计算复杂性：

正+正：直接相加

正+负：比较绝对值大小，用大减小，结果符号由大者决定

负+负：直接相加，符号为负

这种复杂的逻辑导致硬件设计成本增加，这正是计算机科学家需要解决的问题。

二、补码：用模运算将减法转为加法

1. 模运算的启示

让我们从日常生活中熟悉的时钟开始理解模运算：

想象一个12小时制的时钟，它指向10点。如果要调到7点，有两种方式：

逆时针调3格（相当于减法）：10 - 3 = 7
顺时针调9格（相当于加法）：10 + 9 = 19，19模12 = 7

在模12系统中，-3和9是等价的，因为-3 ≡ 9 (mod 12)。

模运算的数学定义 ：对于任意整数x和模m，x mod m的余数r满足：
x=q⋅m+r,0≤r<mx = q \cdot m + r, \quad 0 \leq r < mx=q⋅m+r,0≤r<m

在模12系统中，-3 mod 12 = 9，因为-3 = (-1)·12 + 9。

2. 计算机中的模运算

计算机的8位寄存器本质上是一个"模256"的系统，因为2^8 = 256。

当我们进行8位运算时，超出8位的结果会被自动截断（相当于模256）。

3. 补码的诞生

补码的定义是：对于负数-x，其补码表示为：
$-x$ 补=2n−x $-x$ _{补} = 2^n - x $-x$ 补=2n−x

其中n是位数（8位时，2^8 = 256）。

为什么这样定义？

因为：
$x$ 补+ $-x$ 补=x+(2n−x)=2n≡0(mod2n) \begin{aligned} $x$ {补} + $-x$ {补} &= x + (2^n - x) \\ &= 2^n \\ &\equiv 0 \pmod{2^n} \end{aligned} $x$ 补+ $-x$ 补=x+(2n−x)=2n≡0(mod2n)

这正是我们想要的：x + (-x) = 0。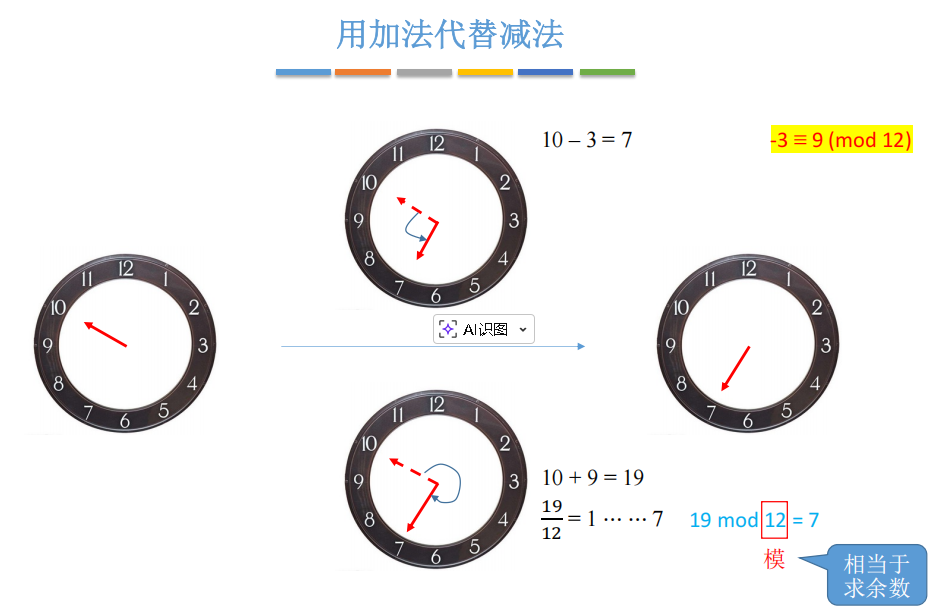

这样做的数学原理是什么呢？

这就跟我们的数论有关了，这里想要深入探讨的同学可以去了解一下数论的带余除数的知识点。

4. 用补码实现减法

回到我们的例子：+14 + (-14)

-14的补码 = 256 - 14 = 242
242的二进制：11110010
14的补码（正数）：00001110

相加：

复制代码

  00001110
+ 11110010
-----------
 100000000

高位进位1被丢弃，结果为00000000（0）

结果正确！

补码的神奇之处：它使计算机只需一个加法器，就能实现加法和减法。

补码的求解方法：

正数：补码 = 原码

负数：补码 = 原码符号位不变，尾数取反，末位加1

例如：-14的原码是10001110，补码是11110010

5. 为什么补码求法是"尾数取反，末位加1"？

考虑-14的补码：

-14的绝对值：00001110
绝对值取反：11110001
末位加1：11110010

为什么这样能得到256 - 14 = 242？

因为：
11110001+1=11110010=(28−1)−14+1=255−14+1=242 \begin{aligned} 11110001 + 1 &= 11110010 \\ &= (2^8 - 1) - 14 + 1 \\ &= 255 - 14 + 1 \\ &= 242 \end{aligned} 11110001+1=11110010=(28−1)−14+1=255−14+1=242

这就是为什么"尾数取反，末位加1"等价于"模 - 绝对值"。

三、移码：便于比较大小

1. 移码的定义

移码（Excess Code）是补码的符号位取反：
$x$ 移= $x$ 补⊕10000000 $x$ {移} = $x$ {补} \oplus 10000000 $x$ 移= $x$ 补⊕10000000

2. 为什么需要移码？

考虑两个有符号数：-14和+14

用补码表示：
- -14：11110010
- +14：00001110
比较大小：需要先判断符号位，如果符号位不同，正数大于负数

用移码表示：

-14：01110010
+14：10001110

移码的神奇之处：移码的大小顺序与真值的大小顺序完全一致！

-128的移码：00000000
-127的移码：00000001
...
0的移码：10000000
...
+127的移码：11111111

移码的作用：在浮点数的阶码（指数部分）表示中，移码使得比较两个浮点数的大小变得非常简单，只需比较它们的移码值（当作无符号数比较即可），无需考虑符号位。

四、反码：历史的过渡

反码是原码到补码的过渡，定义为：

正数：反码 = 原码
负数：反码 = 原码符号位不变，尾数取反

反码的缺陷：

0的表示不唯一：+0 = 00000000，-0 = 11111111
依然需要处理符号位

为什么反码被淘汰：

它没有解决原码的计算问题
它没有解决0的表示问题
它没有比补码更优的特性

五、各种码的总结与作用

编码方式	作用	优势	缺陷	适用场景
原码	直观表示有符号数	符合人类思维	计算复杂，需要专门减法器	仅作理论参考
反码	原码到补码的过渡	比原码稍好	0的表示不唯一，计算复杂	历史过渡，现已淘汰
补码	用加法代替减法	1. 简化硬件设计（只需加法器） 2. 解决0的表示问题 3. 统一加减运算	无	现代计算机整数运算标准
移码	方便比较大小	1. 真值大小与移码大小一致 2. 便于硬件实现比较	仅用于浮点数阶码	浮点数阶码表示

六、为什么补码是计算机的"真神"？

硬件成本大幅降低：只需设计一个加法器，无需设计减法器。
运算统一：加法和减法使用相同的电路，代码更简洁。
解决0的表示问题：补码中0的表示唯一（全0）。
数学原理坚实：基于模运算，有严密的数学基础。

面试高频考点：为什么现代计算机系统中，有符号整数普遍使用补码表示？请从硬件实现和数学原理两个角度回答。

硬件实现角度：简化电路，降低成本

1. 统一加法与减法运算

在补码表示下，减法可以转化为加法：

A−B=A+(−B)

其中 −B 直接用其补码表示。因此，CPU 的算术逻辑单元（ALU）只需一个加法器，无需专门设计减法器。

优势：大幅简化硬件结构，减少晶体管数量，降低芯片面积与功耗。

2. 符号位参与运算，无需特殊处理

在补码中，符号位和其他位一样参与加法运算，进位会自然传播。例如：

复制代码

  00000010  (+2)
+ 11111110  (-2, 即 254 的补码形式)
-----------
1 00000000 → 丢弃进位 → 00000000 (0)

结果正确，且无需额外判断符号或切换运算模式。

优势：控制逻辑简单，时序稳定，提升运算速度。

3. 避免"负零"问题，简化比较与判零

原码/反码中存在 +0 (00000000) 和 -0 (10000000 或 11111111) 两种表示。
补码中 0 的表示唯一 （全 0），使得：
- 判零操作只需检查所有位是否为 0；
- 比较、跳转等指令逻辑更简洁。

优势：减少状态判断，提高指令执行效率。

数学原理角度：模运算的天然契合

1. 基于模 2n 的同余系统

n 位计算机本质上是一个模 2n 的环形计数系统。补码正是利用这一特性：

正数 x 的补码： $x$ 补=x
负数 −x 的补码： $-x$ 补=2n−x

于是：

$x$ 补+ $-x$ 补=x+(2n−x)=2n≡0(mod2n) $x$ {\text{补}} + ${-x}$ {\text{补}} = x + (2^n - x) = 2^n \equiv 0 \pmod{2^n} $x$ 补+ $-x$ 补=x+(2n−x)=2n≡0(mod2n)

结果自动归零，完美符合整数加法群的代数结构。

2. 溢出行为符合模运算规律

当运算结果超出表示范围时，补码的溢出表现为模 2n 截断，这与无符号数的溢出行为一致，便于硬件统一处理。

例如（8 位）：

127+1=128→实际存储为 −128(因为 128≡−128(mod256))

数学一致性：有符号与无符号加法在硬件层面可共用同一套加法电路。

3. 编码空间利用率最大化

8 位共有 28=256 种编码。
补码将它们无缝映射到区间 $-128,127$ ，无浪费、无重叠。
特别地，10000000 被有效用于表示 −128，而不是像原码那样浪费在"-0"上。

七、实例验证

实例1：88 - 66

66的补码 = 256 - 66 = 190 = 10111110
88的补码 = 01011000

相加：

复制代码

  01011000
+ 10111110
-----------
 100010110

丢弃高位进位，结果为00010110 = 22
88 - 66 = 22，结果正确！

实例2：-100 + (-100)

-100的补码 = 256 - 100 = 156 = 10011100

两个-100相加：

复制代码

  10011100
+ 10011100
-----------
 100111000

丢弃高位进位，结果为00111000 = 56
但-100 + (-100) = -200，而8位补码范围是 $-128, 127$ ，-200溢出，结果56是溢出后的错误结果

溢出判断：当两个同号数相加，结果符号与操作数符号不同，即发生溢出。

思考题：为什么8位补码的范围是 $-128, 127$ ，而不是 $-127, 127$ ？请从补码的定义和模运算角度解释。

从补码的定义出发

补码的基本规则（8 位）

正数：补码 = 原码（符号位为 0）
负数：补码 = 28−∣x∣ = 256−∣x∣

这就是补码的数学定义：在模 2n 系统中，负数 −x 的补码等于模减去其绝对值。

正数的最大值

8 位中，最高位是符号位（0 表示正），剩下 7 位用于数值：

最大正数 = 011111112=27−1=127

所以正数范围是：0 到 +127

负数的最小值

我们尝试用补码表示 −128：

$-128$ 补=256−128=128=100000002

这个二进制编码 10000000 是合法的 8 位数，且符号位为 1（符合负数特征）。

再看 −129：

$-129$ 补=256−129=127=011111112

但 01111111 的符号位是 0，会被解释为 +127，而不是 −129！

所以 −129 无法用 8 位补码正确表示。

因此，能表示的最小负数是 −128 ，对应补码 10000000

从模运算和编码空间角度理解

8 位总共能表示多少个不同的数？

8 位二进制共有 28=256 种不同编码。

这些编码必须覆盖：

所有非负整数（包括 0）
所有负整数

补码中"0"是唯一的

$+0$ 补=00000000
$-0$ 补=256−0=256≡0(mod256)→00000000

所以 0 只占用一个编码（不像原码/反码占用两个）

编码分配

总共 256 个编码
其中 1 个用于 0
剩下 255 个用于正数和负数

由于补码的构造方式天然偏向多表示一个负数，分配如下：

类型	数量	范围
正数（含 0）	128 个	0 到 +127
负数	128 个	-1 到 -128

为什么负数能到 -128？因为 10000000 这个原本在原码中表示"-0"的编码，在补码中被重新利用来表示 -128。

这就是"多出来的一个负数"的来源！

八、结语

原码：直观但计算复杂，需要专门的减法器
反码：历史过渡，已无实际应用
补码：用模运算将减法转为加法，简化硬件设计，是现代计算机整数运算的基石
移码：真值大小与移码大小一致，便于硬件比较大小，用于浮点数阶码

理解了这些编码方式的作用，你就理解了计算机如何用最简单的硬件实现最复杂的计算。补码的巧妙设计，是计算机科学中数学与工程完美结合的典范。