机器学习014:监督学习【分类算法】（逻辑回归）-- 一个“是与非”的智慧分类器

今天，我们要认识一位特殊的"朋友"------逻辑回归 （Logistic Regression）。别看名字里有"回归"两个字，它可是个不折不扣的分类大师 ，专门负责回答"是"或"不是"、"好"或"坏"、"A类"或"B类"这类二选一的问题。

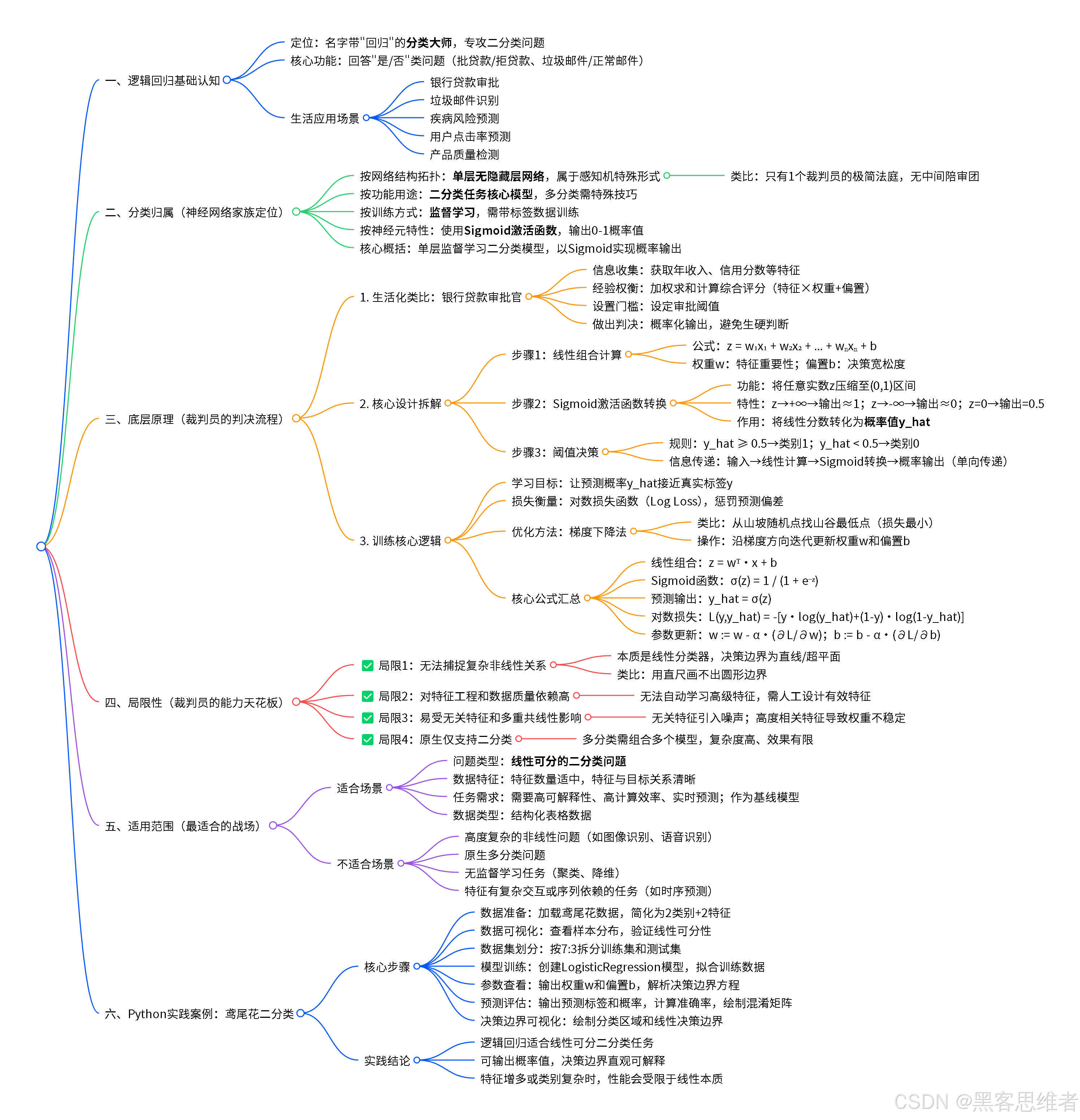
想象一下这些生活场景：

银行要判断："这笔贷款该不该批给这位客户？"
邮箱系统要识别："这封新邮件是正常的，还是垃圾邮件？"
医生要辅助诊断："根据这些体检指标，病人患某种疾病的风险是高还是低？"

这些决策背后，常常就有逻辑回归在默默工作。它就像一个经验丰富的二分法裁判，从复杂的数据中学习规律，然后给出一个清晰的分类判断。

在开始深入之前，我们先给它一个清晰的身份定位。

一、分类归属：它到底属于哪种神经网络？

要理解逻辑回归，我们可以把它放到一个更广阔的"神经网络家族"地图里来看。虽然逻辑回归本身结构简单，但它是理解更复杂神经网络的重要基石。

（注：下文我们用"神经元"来代指一个基础的计算单元，你可以把它想象成一个微型决策器。）

从几个核心维度来看逻辑回归的位置：

按网络结构拓扑（连接方式）划分 ：逻辑回归属于最简单的单层网络 （严格说是"无隐藏层"）。你可以把它想象成一个只有一个"裁判员"的极简法庭 。信息从输入（证据）直接流向输出（判决），中间没有其他"陪审团"或"合议庭"（隐藏层）进行复杂讨论。这种结构也常被称为感知机（Perceptron）的一种特殊形式。
按功能用途划分 ：它是二分类任务 的经典和基础模型。它的核心工作就是划定一条边界，把事物分成两类。虽然通过一些技巧也能处理多分类，但其本质和最擅长的，还是处理"非此即彼"的问题。
按训练方式划分 ：它属于监督学习。这意味着它需要"老师"的指导。我们必须为它提供大量"带标签"的训练数据，比如成千上万封明确标好"正常邮件"或"垃圾邮件"的样本，它才能从中学习规律。
按神经元特性划分 ：它的"裁判员"（神经元）使用了一个非常关键的"理智阀门"------Sigmoid激活函数。这个函数能确保它的输出永远是一个介于0和1之间的概率值，而不是一个天马行空的数字。这一点我们稍后会详细解释。

所以，我们可以这样概括：

逻辑回归，在神经网络家族中，属于按结构拓扑划分的最基础单层网络，是监督学习范式下，专门用于处理二分类任务的利器，其核心特性在于使用Sigmoid函数将输出转化为概率。

明确了它的"家族出身"，我们接下来看看，这个简单的"裁判员"内部，到底是如何进行思考和判断的。

二、底层原理：裁判员如何做出判决？

让我们用一个生活化的类比来拆解逻辑回归的工作流程。

生活类比：银行贷款审批官

假设你是一位银行贷款审批官。你的任务很简单：根据客户的"年收入"和"信用分数"两项信息，决定"批准"或"拒绝"贷款申请。

你的思考过程是怎样的？

信息收集：拿到客户的资料：年收入=X1万元，信用分数=X2分。
经验权衡 ：在你的经验里，年收入越高、信用分数越高，客户越靠谱。你会在心里给这两项信息分配不同的重视程度（权重） 。比如，你可能觉得信用分数比年收入稍微更重要一点。于是，你心里有一个公式：
综合评分 = (年收入 * 权重W1) + (信用分数 * 权重W2) + 基础门槛（偏置b）
综合评分越高，代表客户资质越好。
设置门槛 ：光有综合评分还不够。多高算高？多低算低？你需要一个决策门槛。比如，你设定综合评分超过7分就可以批准。
做出判决 ：计算综合评分。如果远高于7分，你毫不犹豫地"批准"；如果远低于7分，你明确"拒绝"。但如果分数在7分附近，比如6.9分或7.1分呢？现实中你可能会有点犹豫。逻辑回归的精妙之处就在这里------它不直接说"是"或"否"，而是告诉你"是的概率有多大"。

逻辑回归的核心设计拆解

现在，我们把这位"审批官"数字化，看看逻辑回归的具体设计。

1. 核心计算：加权求和与偏置

逻辑回归首先会像审批官一样，对输入的特征（如年收入、信用分数）进行加权求和，并加上一个偏置项。这个计算结果是线性的。

复制代码

线性组合 z = (w1 * x1) + (w2 * x2) + ... + (wn * xn) + b

w1, w2...wn就是权重，代表每个特征的重要性。b是偏置，可以理解为天生的"宽松度"或"严格度"。这些w和b，就是模型要通过学习得到的核心参数。

2. 灵魂部件：Sigmoid激活函数

得到线性分数z后，如果直接用它做判断（比如z>0就批准），那就是一个线性分类器 ，非常生硬。逻辑回归的智慧在于，它把z送入一个叫 "Sigmoid函数" 的转换器。

这个函数长这样（我们用文字描述其效果）：

它能把任何实数z ，神奇地压缩到(0, 1)这个区间内。
当z为正无穷大时，输出无限接近1。
当z为负无穷大时，输出无限接近0。
当z=0时，输出刚好是0.5。

它的图像是一条平滑的、从0到1上升的S形曲线。

为什么要做这个转换？

因为经过Sigmoid函数转换后的输出，可以被完美地解释为一个概率值 ！我们记这个输出为 y_hat。
y_hat = Sigmoid(z)，且 0 < y_hat < 1

3. 信息传递与判决

逻辑回归的信息传递是严格单向 的：输入特征 → 线性计算 → Sigmoid转换 → 输出概率。它没有循环或跳跃连接，结构清晰简单。

最后，我们通常设定一个阈值（比如0.5）来做出最终分类：

如果 y_hat >= 0.5，则预测为 类别1（例如"批准"）。
如果 y_hat < 0.5，则预测为 类别0（例如"拒绝"）。

核心逻辑图示

>=0.5 <0.5 输入特征线性组合z Sigmoid函数输出概率阈值判断类别1 类别0

训练的核心逻辑：如何学习数据特征？

这位"审批官"一开始并不知道权重w和偏置b应该设为多少。它需要通过"学习"（训练）来获得经验。

学习目标 ：让模型的预测概率 y_hat 尽可能接近真实的标签 y（y=1代表批准，y=0代表拒绝）。

如何衡量"接近"程度？ ------ 使用损失函数 。

逻辑回归常用"对数损失函数"（Log Loss）。通俗理解：如果真实情况是"批准"（y=1），而模型预测的概率y_hat很小（比如0.1，意味着它倾向于拒绝），那么这个"错误"就会被这个损失函数狠狠地记上一笔（损失值很大）。反之亦然。

如何优化（学习）？ ------ 使用梯度下降 。

可以把损失函数想象成一个崎岖的山坡，我们的目标是从随机起点（随机的w和b）出发，找到山谷的最低点 （损失最小的点）。梯度下降法就是通过计算"哪个方向是下坡最陡的方向"（梯度），然后朝着这个方向迈出一小步，不断重复这个过程，最终逼近最优的w和b。

这个过程，就是模型从数据中"学习特征规律"的核心逻辑。

核心公式罗列（供了解）

线性组合：z=wT⋅x+bz = w^T · x + bz=wT⋅x+b
Sigmoid函数：σ(z)=1/(1+e−z)σ(z) = 1 / (1 + e^{-z})σ(z)=1/(1+e−z)
预测输出（概率）：yhat=σ(z)y_hat = σ(z)yhat=σ(z)
损失函数（对数损失）：L(y,yhat)=−[y⋅log(yhat)+(1−y)⋅log(1−yhat)]L(y, y_hat) = -[y·log(y_hat) + (1-y)·log(1-y_hat)]L(y,yhat)=−[y⋅log(yhat)+(1−y)⋅log(1−yhat)]
梯度下降更新参数：w:=w−α∗(∂L/∂w),b:=b−α∗(∂L/∂b)w := w - α * (∂L/∂w), b := b - α * (∂L/∂b)w:=w−α∗(∂L/∂w),b:=b−α∗(∂L/∂b) （其中α是学习率，即"步长"）

了解了这位"裁判员"如何工作和学习后，我们必须清醒地认识到，它并非万能。它有自己的能力和边界。

三、局限性：这位裁判员的"能力天花板"

逻辑回归简单而强大，但它的局限性也同样明显，主要源于其极简的设计。

无法直接捕捉复杂的非线性关系
- 是什么 ：逻辑回归本质上是一个线性分类器 。它通过Sigmoid函数包裹了一个线性决策边界。这意味着，它只能在数据空间中画出一条直线（或超平面） 来分割两类数据。
- 为什么 ：因为它的核心计算 z = w·x + b 是线性的。Sigmoid函数只是把这条直线"扭曲"成了概率，但决策边界本身（即z=0这条线）仍然是直线。
- 生活比喻：就像你只用一把直尺，试图在纸上画出一个完美的圆形边界来区分红点和蓝点，这是不可能的。如果红点和蓝点像太极图一样交织在一起，一条直线根本无法有效分开它们。
对特征工程和数据质量依赖度高
- 是什么：逻辑回归模型的好坏，非常依赖于输入特征（x）本身是否有效、是否与问题相关。如果特征不好，模型学不到东西。
- 为什么：它不像深度学习模型（如深层神经网络）那样，有多层网络来自动学习和组合出高级的抽象特征。逻辑回归只能"看"到你给它的原始特征或简单衍生特征。
- 生活比喻：就像一个只会根据"身高"和"体重"判断运动员类型的裁判。如果你不告诉它"肌肉含量"、"体脂率"、"百米速度"这些更相关的特征，它可能永远分不清短跑运动员和相扑选手。
易受无关特征和多重共线性影响
- 是什么：如果输入的特征中，有些是毫无关系的（比如用"星座"预测贷款违约），或者特征之间彼此高度相关（比如"房间数量"和"房屋面积"），会影响模型的稳定性和可解释性。
- 为什么：无关特征会引入噪声，而高度相关的特征会使模型难以确定每个特征独立的贡献，权重估计会变得不稳定。
本质上是二分类器，处理多分类需技巧
- 是什么：一个标准的逻辑回归模型只能输出一个概率，处理"A or B"问题。对于"A or B or C"这类多分类问题，需要采用"一对多"等策略组合多个逻辑回归模型，这增加了复杂性且可能效果不佳。
- 为什么：这是由其输出层（单个Sigmoid神经元）的天然结构决定的。

认识到这些局限，我们就能更准确地知道，该在什么场合邀请这位"裁判员"出场。

四、使用范围：它最适合的战场

基于上述原理和局限，逻辑回归的核心适用场景非常明确：

适合用它解决的问题（什么样的问题适合？）

问题类型 ：二分类问题 ，且两类数据大致是线性可分的（即理论上可以用一条直线/平面分开）。这是它的主场。
数据特征 ：特征数量适中，特征与目标之间的关系相对清晰、直接，不需要非常复杂的非线性变换。
任务需求 ：
- 需要模型具有可解释性 ：逻辑回归的权重w有明确的物理意义（特征的重要性），便于人类理解"模型为什么这么判断"。这在金融、医疗等高风险领域至关重要。
- 对计算资源和速度有要求：模型简单，训练和预测速度极快，占用资源少，适合在线实时预测。
- 作为强基线模型：在任何分类任务开始时，先用逻辑回归建立一个性能基准，再尝试更复杂的模型。

不适合用它解决的问题（什么样的问题不适合？）

高度复杂的非线性分类问题：例如图像识别（猫 vs 狗）、语音识别、自然语言理解中的复杂语义分类。这些任务中，数据间的分界线极其复杂，需要CNN、RNN或深层神经网络来捕捉。
多分类问题：虽然可以通过技巧实现，但并非其设计初衷，效果通常不如专门的多分类模型（如Softmax回归）或更复杂的网络。
无监督学习任务：如聚类、降维。逻辑回归必须有明确的"标签"来指导学习。
特征间有复杂交互或序列依赖的任务：例如预测股票价格的连续波动（时序依赖）、理解一段话的情感（上下文依赖），这些需要LSTM、Transformer等具备序列建模能力的网络。

简而言之，逻辑回归是解决结构化数据 （表格数据）中线性可分二分类问题 的首选"工具刀"，尤其当你需要快速、可解释的解决方案时。

五、应用场景：它在现实世界中的身影

逻辑回归虽然简单，但在各行各业的应用极为广泛。以下是几个贴近生活的具体案例：

金融风控：信用卡欺诈检测
- 场景：当你刷卡消费时，银行系统需要在毫秒级内判断这笔交易是否有欺诈嫌疑。
- 逻辑回归的作用 ：系统会实时提取本次交易的特征，如交易金额、时间、地点、商户类型 ，以及你的历史消费习惯。逻辑回归模型根据这些特征，快速计算出一个"欺诈概率"。如果概率超过某个高风险阈值，系统可能会触发验证短信或暂时冻结卡片，以保护你的资金安全。它的可解释性也帮助风控人员理解是哪个特征（如"深夜在高风险地区大额消费"）触发了警报。
医疗健康：疾病风险预测
- 场景：医院或体检中心希望根据患者的常规检查指标，预测其患某种疾病（如糖尿病）的风险。
- 逻辑回归的作用 ：模型以患者的年龄、体重指数、血压、血糖、血脂等指标作为输入特征。通过学习大量历史病例数据，逻辑回归可以给出一个患病的概率值。医生可以将此作为重要的辅助诊断参考，并对高风险人群进行早期干预和生活指导。模型权重还能揭示哪些指标对疾病影响最大。
互联网营销：用户点击率预测
- 场景：在新闻APP或电商网站，平台需要预测某个用户是否会点击推荐给他的某条新闻或商品广告。
- 逻辑回归的作用 ：这是互联网公司的经典应用。模型的特征可能包括用户画像 （性别、年龄、兴趣标签）、上下文信息 （当前时间、地理位置）、物品属性 （新闻类别、商品价格）以及历史交互行为。逻辑回归计算出点击概率（CTR），排序系统根据CTR高低决定向用户优先展示什么内容，从而实现流量和收入的最大化。其高效性足以应对每秒数百万次的预测请求。
内容安全：垃圾邮件/评论过滤
- 场景：你的邮箱服务商需要自动过滤垃圾邮件；社交平台需要过滤不当评论。
- 逻辑回归的作用 ：模型将邮件或评论的文本内容，通过技术（如词袋模型）转化为数字特征，比如是否包含"免费"、"中奖"、"点击链接"等高频垃圾词汇及其出现频率。逻辑回归通过学习标记好的垃圾/正常样本，学会识别垃圾内容的概率模式，从而实现自动过滤。
生产制造：产品质量检测
- 场景：在生产线末端，需要快速判断刚下线的产品是否合格。
- 逻辑回归的作用 ：通过传感器收集产品的若干关键参数（如尺寸、重量、某个部件的电压值等）。逻辑回归模型根据这些参数，判断产品属于"合格品"还是"瑕疵品"的概率。对于概率处于模糊地带的产品，可以交由人工复检，从而大幅提高质检效率和一致性。

在这些场景中，逻辑回归扮演的角色高度一致：一个高效、可靠、透明的二分类概率估算器，在速度、效果和可解释性之间取得了优秀的平衡。

总结与一句话核心价值

让我们回顾一下今天的旅程。我们从银行贷款的类比出发，认识了逻辑回归这位"二分法裁判"。我们明确了它在神经网络家族中作为基础单层二分类模型 的定位；深入剖析了它通过线性加权、Sigmoid概率化和阈值决策 的核心原理；也客观看到了它无法处理复杂非线性问题 的局限；最后，我们描绘了它在金融、医疗、互联网等领域的广泛应用。

一句话概括逻辑回归的核心价值：

逻辑回归是机器学习中，以极高效率和优秀可解释性，解决线性可分二分类问题的奠基性与实用性模型。

对于初学者而言，学习逻辑回归的重点在于：理解从线性决策到概率输出的转换思想，掌握其训练（通过梯度下降最小化损失）的基本逻辑，并清醒认识其线性本质带来的能力边界。 它是你通往更复杂、更强大AI世界的第一块，也是至关重要的一块基石。

Python 实践案例：鸢尾花分类（二分类简化版）

我们将使用经典的鸢尾花（Iris）数据集，但为了方便演示逻辑回归的二分类特性，我们只取其中两个类别（Setosa和Versicolor）以及两个特征（花瓣长度和花瓣宽度）来构建一个分类器。

python 复制代码

# 导入必要的库
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, confusion_matrix, ConfusionMatrixDisplay

# 1. 加载数据并简化（只取前100个样本，两个类别；只取后两个特征）
iris = datasets.load_iris()
X = iris.data[:100, 2:]  # 只取花瓣长度和花瓣宽度 (特征)
y = iris.target[:100]    # 只取前100个样本的标签 (0: Setosa, 1: Versicolor)

print("数据形状：", X.shape)
print("前5个样本的特征：\n", X[:5])
print("前5个样本的标签：", y[:5])

# 2. 可视化数据，看看是否线性可分
plt.figure(figsize=(8, 6))
plt.scatter(X[y==0, 0], X[y==0, 1], color='red', label='Setosa', alpha=0.7)
plt.scatter(X[y==1, 0], X[y==1, 1], color='blue', label='Versicolor', alpha=0.7)
plt.xlabel('Petal Length (cm)')
plt.ylabel('Petal Width (cm)')
plt.title('Iris Flowers (Binary Classification)')
plt.legend()
plt.grid(True)
plt.show()

# 3. 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
print(f"训练集大小：{X_train.shape[0]}, 测试集大小：{X_test.shape[0]}")

# 4. 创建并训练逻辑回归模型
# 参数说明：
# - solver: 优化算法，'liblinear'适用于小数据集
# - C: 正则化强度的倒数，越小正则化越强，用于防止过拟合
model = LogisticRegression(solver='liblinear', C=1.0, random_state=42)
model.fit(X_train, y_train)

# 5. 查看模型学到的参数（权重和偏置）
print("\n=== 模型学习到的参数 ===")
print("权重 (w1, w2):", model.coef_[0])
print("偏置 (b):", model.intercept_[0])
# 解释：决策边界直线方程为 w1*x1 + w2*x2 + b = 0

# 6. 在测试集上进行预测
y_pred = model.predict(X_test)
y_pred_proba = model.predict_proba(X_test) # 获取预测概率

print("\n=== 测试集预测结果示例 ===")
for i in range(5):
    print(f"样本{i+1}: 真实标签={y_test[i]}, 预测标签={y_pred[i]}, 预测概率=[Setosa: {y_pred_proba[i][0]:.3f}, Versicolor: {y_pred_proba[i][1]:.3f}]")

# 7. 评估模型性能
accuracy = accuracy_score(y_test, y_pred)
print(f"\n=== 模型评估 ===")
print(f"测试集准确率：{accuracy:.4f}")

# 绘制混淆矩阵
cm = confusion_matrix(y_test, y_pred)
disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=['Setosa', 'Versicolor'])
disp.plot(cmap=plt.cm.Blues)
plt.title('Confusion Matrix')
plt.show()

# 8. 可视化决策边界
# 生成网格点
x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
                     np.arange(y_min, y_max, 0.02))

# 预测网格上每个点的类别
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

# 绘制决策边界和区域
plt.figure(figsize=(10, 8))
plt.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.coolwarm) # 背景色区分区域
plt.scatter(X[y==0, 0], X[y==0, 1], color='red', label='Setosa', edgecolors='k')
plt.scatter(X[y==1, 0], X[y==1, 1], color='blue', label='Versicolor', edgecolors='k')

# 绘制决策边界直线（w1*x + w2*y + b = 0）
w1, w2 = model.coef_[0]
b = model.intercept_[0]
# 将直线表示为 y = (-w1*x - b) / w2
boundary_x = np.array([x_min, x_max])
boundary_y = (-w1 * boundary_x - b) / w2
plt.plot(boundary_x, boundary_y, 'k--', linewidth=3, label='Decision Boundary')

plt.xlabel('Petal Length (cm)')
plt.ylabel('Petal Width (cm)')
plt.title('Logistic Regression Decision Boundary')
plt.legend()
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.grid(True)
plt.show()

print("\n=== 实践小结 ===")
print("1. 我们成功用逻辑回归将两种鸢尾花分开。")
print("2. 从图中可见，一条直线就能很好地区分这两类花，这正是逻辑回归擅长的『线性可分』问题。")
print("3. 模型输出了每个样本属于各类别的概率，而不仅仅是硬分类结果。")
print("4. 你可以尝试修改代码，使用所有4个特征，或者尝试区分更难分的Versicolor和Virginica类别，观察逻辑回归的局限。")

代码运行步骤说明：

数据准备：加载鸢尾花数据，并简化成一个干净的二分类问题。
数据可视化：先看看数据分布，直观感受两类花是否能被一条线分开。
划分数据集：分成训练集（用于学习）和测试集（用于评估）。
训练模型：创建逻辑回归模型，并用训练数据"喂"给它，让它学习规律。
查看参数：打印出模型学到的权重和偏置，理解它的"内心公式"。
预测与评估：让模型在没见过的测试集上做预测，并计算准确率。
可视化决策：绘制出模型学到的"分界线"，直观展示它的分类逻辑。

通过这个案例，你将亲手验证逻辑回归如何学习、如何决策，并直观看到其"线性决策边界"的含义。祝你实践愉快，在AI学习的道路上迈出坚实的第一步！