次小生成树

YYDS3142025-12-22 10:53

先上代码。

cpp 复制代码 
/*
1.边权可能为 0, max设为负数
2.赋值max/se_max赋初始值时[0]也需要赋值:[1]的父亲就是父亲初始值0
3.se_max维护时≠max
4.更新max时也要修改se_max 
5.倍增已跳到同一个节点:直接返回答案 
*/
#include <bits/stdc++.h>
using namespace std;
#define ll long long
int n,m;//n 表示点数，m 表示边数
ll find_fa[100005];//表示并查集的父亲
ll fa[100005][18]/*树上倍增数组*/,maxn[100005][18];//max树上倍增
ll lmaxn[100005][18]/*min树上倍增*/,deep[100005];//最小生成树上节点的深度
ll sum,calc,ans=LLONG_MAX;
//sum:最小生成树边权和  calc:所有可以换成某条边的边边权最大值  ans:记录答案 
vector<pair<ll,ll> >g[100005];//最小生成树的建树
struct edge
{//表示一条边 
	ll u,v,w;
	bool operator<(const edge &node)const
	{//定义如何比较两条边
		return w<node.w;
	}
}a[300005];
int find(int x){return (x==find_fa[x])?x:find_fa[x]=find(find_fa[x]);}//并查集 
void kruskal()
{//求出最小生成树并建树 
	for(int i=1; i<=m; i++)
	{
		if(find(a[i].u)==find(a[i].v)) continue;
		find_fa[find(a[i].u)]=find(a[i].v);
		g[a[i].u].push_back({a[i].v,a[i].w});
		g[a[i].v].push_back({a[i].u,a[i].w});
		sum+=a[i].w;
	}
}
void dfs(int u,int fat,int dep)
{//记录最小生成树上所有点的父亲节点以及该点到其父亲边的边权 
	for(int i=0; i<g[u].size(); i++)
	{
		if(g[u][i].first==fat) continue;
		fa[g[u][i].first][0]=u;
		maxn[g[u][i].first][0]=g[u][i].second;
		deep[g[u][i].first]=dep+1;
		dfs(g[u][i].first,u,dep+1);
	}
}
void init()
{//倍增的预处理部分 
	for(int i=1; i<=17; i++)
	{//注意这里必须要先枚举跳多少节点 
		for(int j=1; j<=n; j++)
		{
			//更新最大值和次大值，这里要注意千万不要让次大值和最大值相等
			maxn[j][i]=maxn[j][i-1];
			lmaxn[j][i]=lmaxn[j][i-1];
			if(maxn[fa[j][i-1]][i-1]>maxn[j][i])
			{
				lmaxn[j][i]=maxn[j][i];
				maxn[j][i]=maxn[fa[j][i-1]][i-1];
			}
			if(maxn[fa[j][i-1]][i-1]>lmaxn[j][i]&&maxn[fa[j][i-1]][i-1]<maxn[j][i]) lmaxn[j][i]=maxn[fa[j][i-1]][i-1];
			if(lmaxn[fa[j][i-1]][i-1]>lmaxn[j][i]) lmaxn[j][i]=lmaxn[fa[j][i-1]][i-1];
			fa[j][i]=fa[fa[j][i-1]][i-1];//更新往上跳的父亲节点 
		}
	}
}
int getmax(ll u,ll v,ll forbid)
{//求出所有可以换成某条边的边边权最大值 
	ll maxans=-1;
	if(deep[u]<deep[v]) swap(u,v);
	for(int i=17; i>=0; i--)
	{
		if(deep[fa[u][i]]>=deep[v])
		{
			if(maxn[u][i]!=forbid) maxans=max(maxans,maxn[u][i]);//注意不要让答案和最小生成树边权和相等，下面同理 
			else maxans=max(maxans,lmaxn[u][i]);
			u=fa[u][i];
		}
	}
	for(int i=17; i>=0; i--)
	{
		if(fa[u][i]!=fa[v][i])
		{
			if(maxn[u][i]!=forbid) maxans=max(maxans,maxn[u][i]);
			else maxans=max(maxans,lmaxn[u][i]);
			if(maxn[v][i]!=forbid) maxans=max(maxans,maxn[v][i]);
			else maxans=max(maxans,lmaxn[v][i]);
			u=fa[u][i];
			v=fa[v][i];
		}
	}
	if(u==v) return maxans;//注意已经跳到同一个节点了就直接返回最大值 
	if(maxn[u][0]!=forbid) maxans=max(maxans,maxn[u][0]);
	else maxans=max(maxans,lmaxn[u][0]);
	if(maxn[v][0]!=forbid) maxans=max(maxans,maxn[v][0]);
	else maxans=max(maxans,lmaxn[v][0]);
	return maxans;
}
int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin>>n>>m;
	for(int i=1; i<=n; i++) find_fa[i]=i;
	memset(maxn,-0x3f,sizeof(maxn));
	memset(lmaxn,-0x3f,sizeof(lmaxn));
	for(int i=1; i<=m; i++) cin>>a[i].u>>a[i].v>>a[i].w;
	sort(a+1,a+m+1);
	kruskal();
	dfs(1,0,0);
	init();
	for(int i=1; i<=m; i++)
	{
		calc=getmax(a[i].u,a[i].v,a[i].w);
		if(calc>=0)ans=min(ans,sum-calc+a[i].w);
	}
	cout<<ans;
}

/*

1.边权可能为 0, max设为负数

2.赋值max/se_max赋初始值时[0]也需要赋值:[1]的父亲就是父亲初始值0

3.se_max维护时≠max

4.更新max时也要修改se_max

5.倍增已跳到同一个节点:直接返回答案

*/

#include <bits/stdc++.h>

using namespace std;

#define ll long long

int n,m;//n 表示点数，m 表示边数

ll find_fa[100005];//表示并查集的父亲

ll fa[100005][18]/*树上倍增数组*/,maxn[100005][18];//max树上倍增

ll lmaxn[100005][18]/*min树上倍增*/,deep[100005];//最小生成树上节点的深度

ll sum,calc,ans=LLONG_MAX;

//sum:最小生成树边权和 calc:所有可以换成某条边的边边权最大值 ans:记录答案

vector<pair<ll,ll> >g[100005];//最小生成树的建树

struct edge

{//表示一条边

ll u,v,w;

bool operator<(const edge &node)const

{//定义如何比较两条边

return w<node.w;

}

}a[300005];

int find(int x){return (x==find_fa[x])?x:find_fa[x]=find(find_fa[x]);}//并查集

void kruskal()

{//求出最小生成树并建树

for(int i=1; i<=m; i++)

{

if(find(a[i].u)==find(a[i].v)) continue;

find_fa[find(a[i].u)]=find(a[i].v);

g[a[i].u].push_back({a[i].v,a[i].w});

g[a[i].v].push_back({a[i].u,a[i].w});

sum+=a[i].w;

}

}

void dfs(int u,int fat,int dep)

{//记录最小生成树上所有点的父亲节点以及该点到其父亲边的边权

for(int i=0; i<g[u].size(); i++)

{

if(g[u][i].first==fat) continue;

fa[g[u][i].first][0]=u;

maxn[g[u][i].first][0]=g[u][i].second;

deep[g[u][i].first]=dep+1;

dfs(g[u][i].first,u,dep+1);

}

}

void init()

{//倍增的预处理部分

for(int i=1; i<=17; i++)

{//注意这里必须要先枚举跳多少节点

for(int j=1; j<=n; j++)

{

//更新最大值和次大值，这里要注意千万不要让次大值和最大值相等

maxn[j][i]=maxn[j][i-1];

lmaxn[j][i]=lmaxn[j][i-1];

if(maxn[fa[j][i-1]][i-1]>maxn[j][i])

{

lmaxn[j][i]=maxn[j][i];

maxn[j][i]=maxn[fa[j][i-1]][i-1];

}

if(maxn[fa[j][i-1]][i-1]>lmaxn[j][i]&&maxn[fa[j][i-1]][i-1]<maxn[j][i]) lmaxn[j][i]=maxn[fa[j][i-1]][i-1];

if(lmaxn[fa[j][i-1]][i-1]>lmaxn[j][i]) lmaxn[j][i]=lmaxn[fa[j][i-1]][i-1];

fa[j][i]=fa[fa[j][i-1]][i-1];//更新往上跳的父亲节点

}

}

}

int getmax(ll u,ll v,ll forbid)

{//求出所有可以换成某条边的边边权最大值

ll maxans=-1;

if(deep[u]<deep[v]) swap(u,v);

for(int i=17; i>=0; i--)

{

if(deep[fa[u][i]]>=deep[v])

{

if(maxn[u][i]!=forbid) maxans=max(maxans,maxn[u][i]);//注意不要让答案和最小生成树边权和相等，下面同理

else maxans=max(maxans,lmaxn[u][i]);

u=fa[u][i];

}

}

for(int i=17; i>=0; i--)

{

if(fa[u][i]!=fa[v][i])

{

if(maxn[u][i]!=forbid) maxans=max(maxans,maxn[u][i]);

else maxans=max(maxans,lmaxn[u][i]);

if(maxn[v][i]!=forbid) maxans=max(maxans,maxn[v][i]);

else maxans=max(maxans,lmaxn[v][i]);

u=fa[u][i];

v=fa[v][i];

}

}

if(u==v) return maxans;//注意已经跳到同一个节点了就直接返回最大值

if(maxn[u][0]!=forbid) maxans=max(maxans,maxn[u][0]);

else maxans=max(maxans,lmaxn[u][0]);

if(maxn[v][0]!=forbid) maxans=max(maxans,maxn[v][0]);

else maxans=max(maxans,lmaxn[v][0]);

return maxans;

}

int main()

{

ios::sync_with_stdio(0);

cin.tie(0);

cin>>n>>m;

for(int i=1; i<=n; i++) find_fa[i]=i;

memset(maxn,-0x3f,sizeof(maxn));

memset(lmaxn,-0x3f,sizeof(lmaxn));

for(int i=1; i<=m; i++) cin>>a[i].u>>a[i].v>>a[i].w;

sort(a+1,a+m+1);

kruskal();

dfs(1,0,0);

init();

for(int i=1; i<=m; i++)

{

calc=getmax(a[i].u,a[i].v,a[i].w);

if(calc>=0)ans=min(ans,sum-calc+a[i].w);

}

cout<<ans;

}

这是我见到的最长的图论竞赛代码。（截至2025.12）

借鉴了一篇CSDN，可惜不是正解，但还是非常感谢。^_^

资料1

回到正题。

一、基本概念

1.1 什么是最小生成树（MST）？

  • 对于带权连通无向图，生成树是包含所有顶点的无环连通子图

  • 最小生成树 是所有生成树中边权之和最小的

1.2 什么是次小生成树（SMST）？

  • 严格次小生成树 ：边权之和严格大于 最小生成树，但在所有生成树中第二小

  • 非严格次小生成树 ：边权之和不小于最小生成树

复制代码 
示例图：(鸣谢Deep***k)
        5
    A ----- B
    | \     |
   3|  1\   |2
    |     \ |
    C ----- D
        4
    
最小生成树：A-C(3), C-D(4), D-B(2) 总权值 = 9
次小生成树：A-B(5), A-C(3), C-D(4) 总权值 = 12

二、算法思路

2.1 核心思想

复制代码 
次小生成树 = 最小生成树 - 一条树边 + 一条非树边
但必须保证：
1. 加入的非树边(u,v)会形成环
2. 删除的树边在环中，且尽可能大
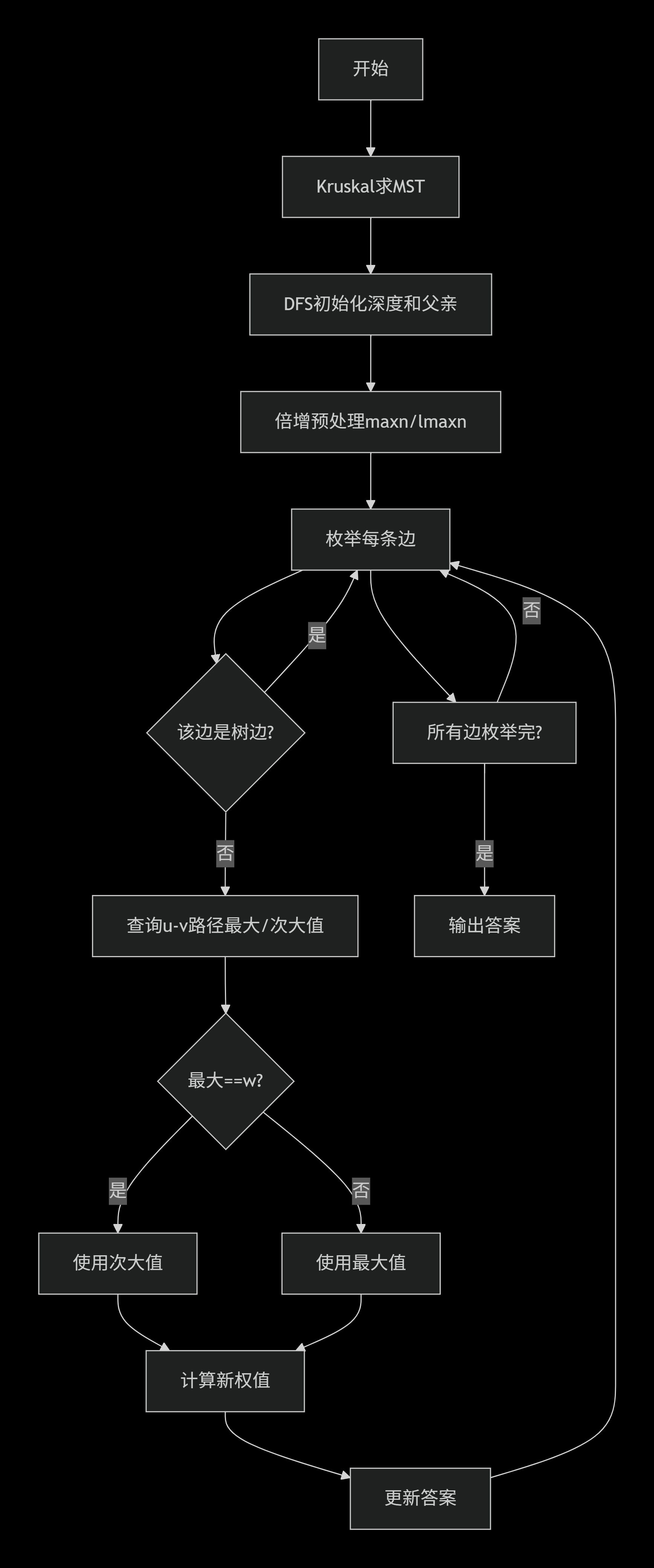
3. 新边权 > 删除边权（严格次小）

2.2 算法步骤

复制代码 
Step 1: 使用Kruskal或Prim求最小生成树MST，记录总权值sum
Step 2: 在MST上预处理树上路径的最大值和次大值
Step 3: 枚举每条非树边(u,v,w)
Step 4: 找到MST中u到v路径上的最大边权max_w
        如果max_w == w，则找次大边权sec_w
Step 5: 计算新生成树权值 = sum - max_w/sec_w + w
Step 6: 取所有结果的最小值

三、代码实现详解

3.1 数据结构定义

cpp 复制代码 
// 边结构体
struct edge
{
    int u, v, w;
    bool operator<(const edge &node)const
    {
        return w < node.w;
    }
}a[300005];

// 关键数组
int fa[100005][18];     // 倍增父亲节点，fa[i][j]表示i向上跳2^j的节点
int maxn[100005][18];   // 路径最大值，maxn[i][j]表示i到fa[i][j]路径的最大边权
int lmaxn[100005][18];  // 路径次大值（严格小于最大值）
int deep[100005];       // 节点深度
vector<pair<int,int>> g[100005]; // MST的邻接表
复制代码 
// 边结构体
struct edge
{
    int u, v, w;
    bool operator<(const edge &node)const
    {
        return w < node.w;
    }
}a[300005];

// 关键数组
int fa[100005][18];     // 倍增父亲节点，fa[i][j]表示i向上跳2^j的节点
int maxn[100005][18];   // 路径最大值，maxn[i][j]表示i到fa[i][j]路径的最大边权
int lmaxn[100005][18];  // 路径次大值（严格小于最大值）
int deep[100005];       // 节点深度
vector<pair<int,int>> g[100005]; // MST的邻接表

3.2 关键步骤表格说明

步骤 函数名 功能 时间复杂度
1 kruskal() 求最小生成树并建树 O(m log m)
2 dfs() 初始化深度、父亲、边权 O(n)
3 init() 倍增预处理最大/次大值 O(n log n)
4 getmax() 查询路径上≠forbid的最大值 O(log n)
5 主循环 枚举所有边，计算次小生成树 O(m log n)

3.3 倍增预处理详解

为什么需要次大值？
复制代码 
 假设路径上的边权为：3, 5, 5, 7
 最大值 = 7
 严格次大值 = 5（注意：不是第二个5，因为要严格小于最大值）

 当非树边权值w=7时，我们不能用最大值替换（否则还是MST）
 需要用次大值5替换，得到sum - 5 + 7 > sum
预处理递推关系
cpp 复制代码 
for (int i = 1; i <= MAXN; i++) {
    for (int j = 1; j <= n; j++) {
        // 从j跳2^(i-1)到中间点mid
        int mid = fa[j][i-1];
        
        // 更新最大值
        maxn[j][i] = max(maxn[j][i-1], maxn[mid][i-1]);
        
        // 更新次大值（关键！必须严格小于最大值）
        lmaxn[j][i] = max(lmaxn[j][i-1], lmaxn[mid][i-1]);
        if (maxn[j][i-1] < maxn[j][i] && maxn[j][i-1] > lmaxn[j][i])
            lmaxn[j][i] = maxn[j][i-1];
        if (maxn[mid][i-1] < maxn[j][i] && maxn[mid][i-1] > lmaxn[j][i])
            lmaxn[j][i] = maxn[mid][i-1];
        
        fa[j][i] = fa[mid][i-1];  // 更新父亲
    }
}
复制代码 
for (int i = 1; i <= MAXN; i++) {
    for (int j = 1; j <= n; j++) {
        // 从j跳2^(i-1)到中间点mid
        int mid = fa[j][i-1];
        
        // 更新最大值
        maxn[j][i] = max(maxn[j][i-1], maxn[mid][i-1]);
        
        // 更新次大值（关键！必须严格小于最大值）
        lmaxn[j][i] = max(lmaxn[j][i-1], lmaxn[mid][i-1]);
        if (maxn[j][i-1] < maxn[j][i] && maxn[j][i-1] > lmaxn[j][i])
            lmaxn[j][i] = maxn[j][i-1];
        if (maxn[mid][i-1] < maxn[j][i] && maxn[mid][i-1] > lmaxn[j][i])
            lmaxn[j][i] = maxn[mid][i-1];
        
        fa[j][i] = fa[mid][i-1];  // 更新父亲
    }
}

3.4 路径查询算法（LCA思路）

复制代码 
查询u到v路径上≠forbid的最大边权：

1. 先将u和v调整到同一深度
   while (deep[u] > deep[v]) {
       用maxn[u][i]更新答案
       u = fa[u][i]
   }

2. 同时向上跳，直到到达LCA
   while (u != v) {
       如果fa[u][i] != fa[v][i]，则更新两边的最大值
       然后u和v同时向上跳
   }

3. 注意：每次比较都要跳过等于forbid的值

再次鸣谢Deep***k.

四、关键问题与解决方案

4.1 问题汇总表

问题 原因 解决方案
边权为0 初始值设为0会导致误判 初始化为负无穷
次大值等于最大值 违反"严格"次小 维护时确保严格小于
答案等于MST权值 替换的边权相同 检查新边权>旧边权
父节点初始值 1号节点的父亲是0 深度和最大值都要正确初始化

4.2 示例分析

复制代码 
输入示例：
7 15
...（边列表）

执行过程：
1. Kruskal得到MST边权总和sum
2. 预处理树上路径信息
3. 对每条非树边(a[i].u, a[i].v, a[i].w)：
   - 查询MST中u到v路径的最大值max_w
   - 如果max_w == a[i].w，查询次大值sec_w
   - 计算new_sum = sum - max_w/sec_w + a[i].w
   - 更新ans = min(ans, new_sum)

五、复杂度分析

操作 时间复杂度 空间复杂度
Kruskal排序 O(m log m) O(m)
Kruskal建树 O(m α(n)) O(n)
DFS初始化 O(n) O(n)
倍增预处理 O(n log n) O(n log n)
查询路径 O(log n) O(1)
总复杂度 O(m log n) O(n log n)

六、优化技巧

  1. 内存优化：如果n很大，可以使用链式前向星代替vector

  2. 常数优化：预处理log值，避免重复计算

  3. 剪枝：如果当前非树边权值大于等于ans-sum+max_w，可以跳过

  4. 并行查询：同时维护严格次大值，避免二次查询

七、常见错误

复制代码 
// 错误1：次大值更新不严格
if (val > lmaxn && val < maxn)  // 正确
if (val > lmaxn && val <= maxn) // 错误！不能等于最大值

// 错误2：忘记处理跳到同一节点的情况
if (u == v) return maxans;  // 必须及时返回

// 错误3：初始值设置不当
memset(maxn, -0x3f, sizeof(maxn));  // 正确：设为很小的负数
memset(maxn, 0, sizeof(maxn));      // 错误：边权可能为0

八、其他

  1. 严格第k小生成树：多次替换，使用堆维护候选方案

  2. 动态最小生成树：支持边权修改，使用LCT维护

  3. 最小度限制生成树：指定某个点的度数

  4. P4180

相关推荐
杜子不疼.2 小时前
【LeetCode 35 & 69_二分查找】搜索插入位置 & x的平方根
算法·leetcode·职场和发展
xu_yule2 小时前
算法基础（区间DP）
数据结构·c++·算法·动态规划·区间dp
天骄t2 小时前
信号VS共享内存：进程通信谁更强？
算法
biter down2 小时前
C++ 交换排序算法：从基础冒泡到高效快排
c++·算法·排序算法
LYFlied2 小时前
【每日算法】LeetCode 226. 翻转二叉树
前端·算法·leetcode·面试·职场和发展
落羽的落羽2 小时前
【C++】深入浅出“图”——图的遍历与最小生成树算法
linux·服务器·c++·人工智能·算法·机器学习·深度优先
txp玩Linux2 小时前
rk3568上webrtc处理稳态噪声实践
算法·webrtc
CoovallyAIHub2 小时前
从空地对抗到空战：首个无人机间追踪百万级基准与时空语义基线MambaSTS深度解析
深度学习·算法·计算机视觉
"YOUDIG"2 小时前
从算法到3D美学——一站式生成个性化手办风格照片
算法·3d
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03Linux下V2Ray安装配置指南04在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）05BongoCat - 跨平台键盘猫动画工具06安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）07jdk21下载、安装（Windows、Linux、macOS）08Labelme从安装到标注：零基础完整指南09CentOS的ISO镜像下载10Open-AutoGLM Windows 安装部署教程