拓扑排序
1 有向⽆环图
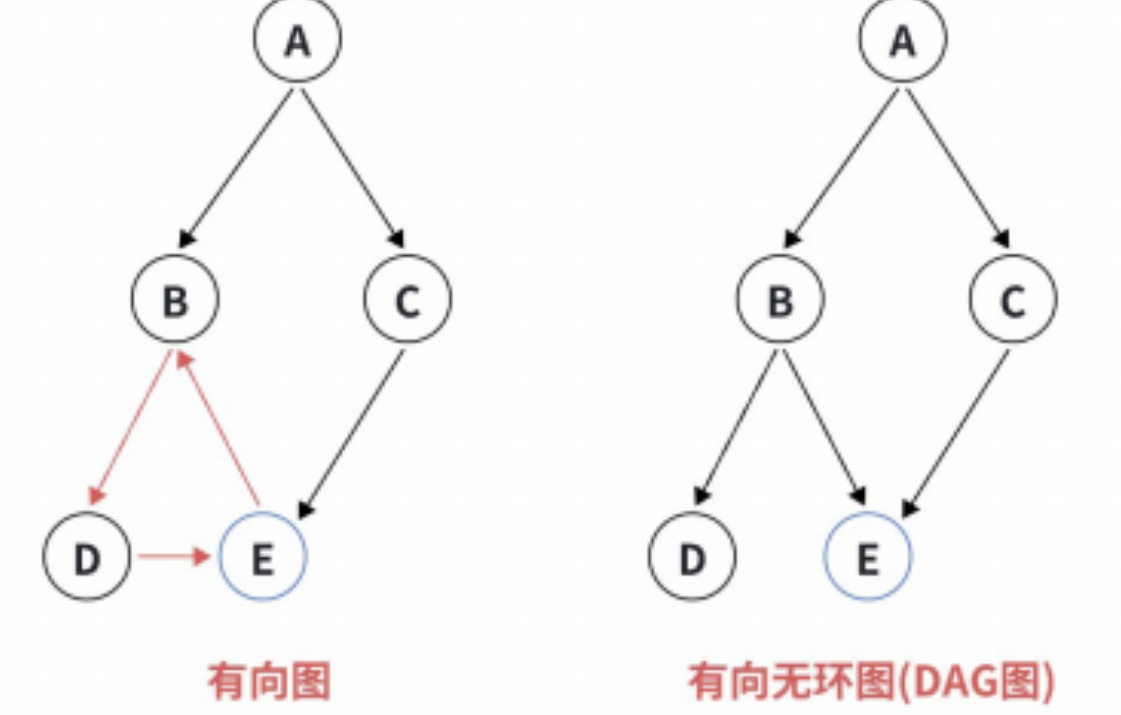
若⼀个有向图中不存在回路,则称为 有向⽆环图 (directed acycline graph),简称 DAG 图。
2. AOV ⽹
举⼀个现实中的例⼦:课程的学习是有优先次序的,如果规划不当会严重影响学习效果。课程间的先 后次序可以⽤有向图表⽰:
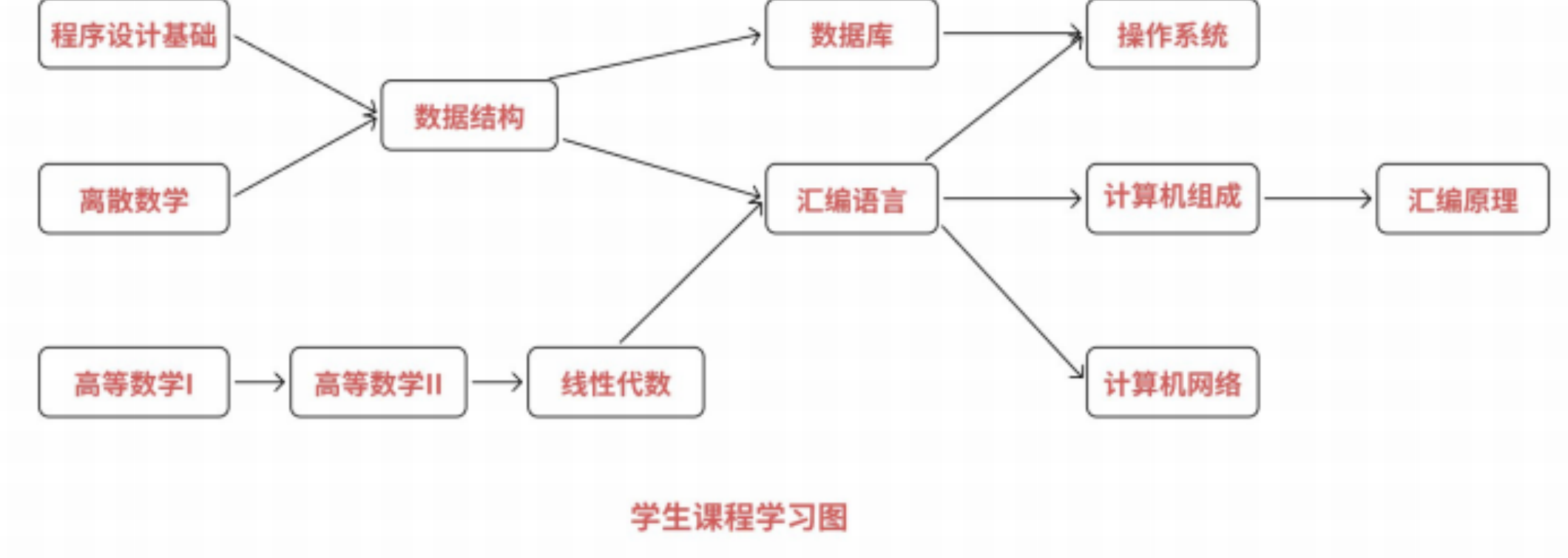
在这种有向图中,⽤顶点表⽰活动,⽤有向边 < Vi , Vj > 表⽰活动 Vi 必须先于活动 Vj进⾏,这种有 向图叫做顶点表⽰活动的⽹络(Activity On Vertex Network),简称 AOV ⽹。
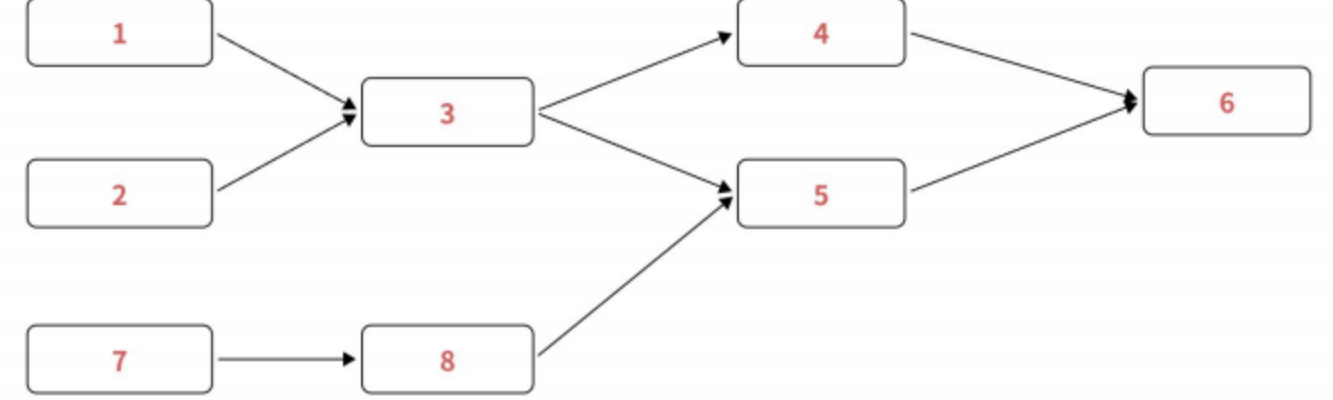
AOV ⽹中不能有回路,否则就不能确定回路中的活动究竟哪个先实施。因此⼀个可⾏的 AOV ⽹必须是 有向⽆环图。
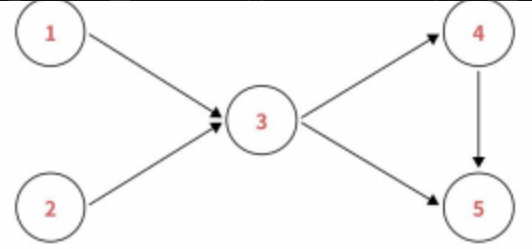
3 拓扑排序
拓扑排序的⽬标是将有向⽆环图中的所有结点排序 ,使得排在前⾯的结点不能依赖于排在后⾯的结
点。在课程问题中,相当于就是找到⼀个排课的合法顺序。具体流程可借助 队列 进⾏:
1. 将图中所有⼊度为 0 的点,加⼊到队列中;
2. 取出队头元素,删除与该点相连的边。如果删除之后的后继结点的⼊度变为 0,加⼊到队列中;
3. 重复 2 操作,直到图中没有点或者没有⼊度为 0 的点为⽌。
拓扑排序判断是否有环:
跑⼀遍拓扑排序算法,如果有结点没有进队,那么就表明有环。
4 【模板】拓扑排序
题⽬来源: 洛⾕
题⽬链接: B3644 【模板】拓扑排序 / 家谱树
难度系数: ★★
题目描述
有个人的家族很大,辈分关系很混乱,请你帮整理一下这种关系。给出每个人的后代的信息。输出一个序列,使得每个人的后辈都比那个人后列出。
输入格式
第 1 行一个整数 N(1≤N≤100),表示家族的人数。接下来 N 行,第 i 行描述第 i 个人的后代编号 ai,j,表示 ai,j 是 i 的后代。每行最后是 0 表示描述完毕。
输出格式
输出一个序列,使得每个人的后辈都比那个人后列出。如果有多种不同的序列,输出任意一种即可。
输入输出样例
输入 #1复制
5
0
4 5 1 0
1 0
5 3 0
3 0输出 #1复制
2 4 5 3 1【解法】
模板题~
【参考代码】
cpp
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
const int N = 110; // 家族人数上限(100),设110留余量
int n; // 实际家族人数
vector<int> edges[N]; // 邻接表:edges[x]存x的所有后代(x→后代的边)
int in[N]; // in[y]:y的入度(y有多少个长辈)
int main()
{
cin >> n; // 输入家族人数n
// 第一步:读入每个人的后代信息,构建图+统计入度
for(int i = 1; i <= n; i++) // 遍历第i个人
{
int j;
// 循环读入i的后代编号,直到读到0结束
while(cin >> j, j) // 等价于cin>>j; while(j!=0)
{
edges[i].push_back(j); // 记录i的后代j(加边i→j)
in[j]++; // j的入度+1(j多了一个长辈i)
}
}
// 第二步:拓扑排序核心(用队列实现)
queue<int> q; // 队列存"入度为0的节点"(没有长辈的人,可优先输出)
// 先把所有入度为0的节点加入队列
for(int i = 1; i <= n; i++)
{
if(in[i] == 0) q.push(i);
}
// 第三步:处理队列,生成拓扑序
while(q.size()) // 队列不为空
{
int x = q.front(); // 取出队首节点(当前无长辈的人)
q.pop(); // 弹出队首
cout << x << " "; // 输出该节点(加入序列)
// 遍历x的所有后代y,相当于"删除x→y的边"
for(auto y : edges[x])
{
in[y]--; // y的入度-1(少了一个长辈x的约束)
if(in[y] == 0) // y的入度为0→没有其他长辈了,可输出
{
q.push(y);
}
}
}
return 0;
}5 摄像头
题⽬来源: 洛⾕
题⽬链接: P2712 摄像头
难度系数: ★★
题目描述
食品店里有 n 个摄像头,这种摄像头很笨拙,只能拍摄到固定位置。现有一群胆大妄为的松鼠想要抢劫食品店,为了不让摄像头拍下他们犯罪的证据,他们抢劫前的第一件事就是砸毁这些摄像头。
为了便于砸毁摄像头,松鼠歹徒们把所有摄像头和摄像头能监视到的地方统一编号,一个摄像头能被砸毁的条件是该摄像头所在位置不被其他摄像头监视。
现在你的任务是帮松鼠们计算是否可以砸掉所有摄像头,如不能则输出还没砸掉的摄像头的数量。
输入格式
第 1 行,一个整数 n,表示摄像头的个数。
第 2 到 n+1 行是摄像头的信息,包括:摄像头的位置 x,以及这个摄像头可以监视到的位置数 m,之后 m 个数 y 是此摄像头可以监视到的位置(砸了这些摄像头之后自然这些位置就监视不到了)。
输出格式
若可以砸掉所有摄像头则输出" YES",否则输出还没砸掉的摄像头的数量(不带引号)。
输入输出样例
输入 #1复制
5
1 1 2
2 1 1
3 1 7
4 1 1
5 0输出 #1复制
2说明/提示
1≤n≤100。
0≤m≤100。
0≤x,y≤500。
【解法】
拓扑排序判断是否有环。
直接跑⼀遍拓扑排序,然后统计⼀下有多少摄像头没有出队。那么这些没有出队的摄像头就是环⾥⾯ 的元素。
注意:
• 有些位置可能没有摄像头,需要判断⼀下。
【参考代码】
cpp
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
const int N = 510; // 位置编号上限是500,设510留余量
int n; // 摄像头的个数
vector<int> edges[N]; // 邻接表:edges[x]存x能监视的所有位置(x→y的边)
int in[N]; // in[y]:位置y的入度(有多少个摄像头监视y)
bool st[N]; // st[x]=true → 位置x有摄像头(标记有效顶点)
int main()
{
cin >> n; // 输入摄像头个数n
// 第一步:读入摄像头信息,构建图+标记有效顶点+统计入度
for(int i = 1; i <= n; i++) // 遍历第i个摄像头
{
int x, m, y;
cin >> x >> m; // x=摄像头位置,m=能监视的位置数
st[x] = true; // 标记:位置x有摄像头(有效顶点)
while(m--) // 读入m个被监视的位置y
{
cin >> y;
edges[x].push_back(y); // 加边x→y(x监视y)
in[y]++; // y的入度+1(多一个摄像头监视y)
}
}
// 第二步:拓扑排序初始化------入度为0的有效顶点加入队列
queue<int> q;
for(int i = 0; i <= 500; i++) // 遍历所有可能的位置(0~500)
{
// 条件:位置i有摄像头(st[i]=true)且入度为0(in[i]=0)
if(st[i] && in[i] == 0)
q.push(i);
}
// 第三步:执行拓扑排序,消除入度为0的顶点
while(q.size()) // 队列不为空
{
auto x = q.front(); // 取出队首位置x(入度为0的有效顶点)
q.pop(); // 弹出队首
// 遍历x能监视的所有位置y(遍历边x→y)
for(auto y : edges[x])
{
in[y]--; // y的入度-1(x的摄像头被砸了,不再监视y)
// 如果y是有效顶点(有摄像头)且入度变为0,加入队列
if(st[y] && in[y] == 0)
q.push(y);
}
}
// 第四步:统计环中的顶点数(砸不掉的摄像头数)
int ret = 0;
for(int i = 0; i <= 500; i++)
{
// 条件:位置i有摄像头(st[i]=true)且入度>0(还在环里)
if(st[i] && in[i])
ret++;
}
// 输出结果:没砸掉的数量为0则输出YES,否则输出数量
if(ret == 0) cout << "YES" << endl;
else cout << ret << endl;
return 0;
}6 最⼤⻝物链计数
题⽬来源: 洛⾕
题⽬链接: P4017 最⼤⻝物链计数
难度系数: ★★★
题目背景
你知道食物链吗?Delia 生物考试的时候,数食物链条数的题目全都错了,因为她总是重复数了几条或漏掉了几条。于是她来就来求助你,然而你也不会啊!写一个程序来帮帮她吧。
题目描述
给你一个食物网,你要求出这个食物网中最大食物链的数量。
(这里的"最大食物链",指的是生物学意义上的食物链 ,即最左端是不会捕食其他生物的生产者,最右端是不会被其他生物捕食的消费者。)
Delia 非常急,所以你只有 1 秒的时间。
由于这个结果可能过大,你只需要输出总数模上 80112002 的结果。
输入格式
第一行,两个正整数 n、m,表示生物种类 n 和吃与被吃的关系数 m。
接下来 m 行,每行两个正整数,表示被吃的生物 A 和吃 A 的生物 B。
输出格式
一行一个整数,为最大食物链数量模上 80112002 的结果。
输入输出样例
输入 #1复制
5 7
1 2
1 3
2 3
3 5
2 5
4 5
3 4输出 #1复制
5说明/提示
各测试点满足以下约定:
| 测试点编号 | n | m |
|---|---|---|
| 1,2 | ≤40 | ≤400 |
| 3,4 | ≤100 | ≤2×103 |
| 5,6 | ≤103 | ≤6×104 |
| 7,8 | ≤2×103 | ≤2×105 |
| 9,10 | ≤5×103 | ≤5×105 |
对于 100% 的数据,1≤n≤5×103,1≤m≤5×105
【补充说明】
数据中不会出现环,满足生物学的要求。(感谢 @AKEE)
【解法】
注意审题!题⽬问的是⼀共有多少条路径!
拓扑排序的过程中,进⾏动态规划。
对于每⼀个节点 ,通过它的路径为:前驱所有结点的路径总数之和。因此,可以在拓扑排序的过程 中,维护从起点开始到达每⼀个节点的路径总数。
【参考代码】
cpp
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
// 常量:N=生物种类上限(5010),MOD=取模值(题目要求)
const int N = 5010, MOD = 80112002;
int n, m; // n=生物种类数,m=吃与被吃的关系数
vector<int> edges[N]; // 邻接表:edges[x]存x被哪些生物吃(x→y,y吃x)
int in[N], out[N]; // in[y]=y的入度(有多少生物被y吃→y的食物数);out[x]=x的出度(x被多少生物吃)
int f[N]; // f[i]=到生物i的食物链数量
int main()
{
cin >> n >> m; // 输入生物数n,关系数m
// 第一步:读入吃与被吃关系,构建图+统计入度/出度
for(int i = 1; i <= m; i++)
{
int x, y; cin >> x >> y; // x被y吃 → 边x→y
edges[x].push_back(y); // 加边x→y(x的后继是y)
in[y]++; // y的入度+1(y多了一个食物x)
out[x]++; // x的出度+1(x多了一个捕食者y)
}
// 第二步:拓扑排序初始化------生产者(入度为0)加入队列,f值=1
queue<int> q;
for(int i = 1; i <= n; i++)
{
if(in[i] == 0) // 生产者:没有生物被它吃(它不吃任何生物)
{
f[i] = 1; // 到生产者的路径数=1(只有自己)
q.push(i); // 加入拓扑队列
}
}
// 第三步:拓扑排序+动态规划统计路径数
while(q.size()) // 队列不为空
{
auto x = q.front(); // 取出队首生物x(当前无前置依赖的生物)
q.pop(); // 弹出队首
// 遍历x的所有捕食者y(x被y吃,边x→y)
for(auto y : edges[x])
{
// 到y的路径数 += 到x的路径数(因为x→y是一条新路径),取模避免溢出
f[y] = (f[y] + f[x]) % MOD;
in[y]--; // y的入度-1(x已经处理完,y少了一个食物依赖)
// 如果y的入度为0(所有食物都处理完),加入队列
if(in[y] == 0)
q.push(y);
}
}
// 第四步:统计所有顶级消费者(出度为0)的路径数之和
int ret = 0;
for(int i = 1; i <= n; i++)
{
if(out[i] == 0) // 顶级消费者:没有捕食者(不被任何生物吃)
{
ret = (ret + f[i]) % MOD; // 累加路径数,取模
}
}
// 输出结果
cout << ret << endl;
return 0;
}7 杂物
题⽬来源: 洛⾕
题⽬链接: P1113 杂务
难度系数: ★★★
题目描述
John 的农场在给奶牛挤奶前有很多杂务要完成,每一项杂务都需要一定的时间来完成它。比如:他们要将奶牛集合起来,将他们赶进牛棚,为奶牛清洗乳房以及一些其它工作。尽早将所有杂务完成是必要的,因为这样才有更多时间挤出更多的牛奶。
当然,有些杂务必须在另一些杂务完成的情况下才能进行。比如:只有将奶牛赶进牛棚才能开始为它清洗乳房,还有在未给奶牛清洗乳房之前不能挤奶。我们把这些工作称为完成本项工作的准备工作。至少有一项杂务不要求有准备工作,这个可以最早着手完成的工作,标记为杂务 1。
John 有需要完成的 n 个杂务的清单,并且这份清单是有一定顺序的,杂务 k (k>1) 的准备工作只可能在杂务 1 至 k−1 中。
写一个程序依次读入每个杂务的工作说明。计算出所有杂务都被完成的最短时间。当然互相没有关系的杂务可以同时工作,并且,你可以假定 John 的农场有足够多的工人来同时完成任意多项任务。
输入格式
第 1 行,一个整数 n (3≤n≤10,000),必须完成的杂务的数目;
第 2 至 n+1 行,每行有一些用空格隔开的整数,分别表示:
- 工作序号(保证在输入文件中是从 1 到 n 有序递增的);
- 完成工作所需要的时间 len (1≤len≤100);
- 一些必须完成的准备工作,总数不超过 100 个,由一个数字 0 结束。有些杂务没有需要准备的工作只描述一个单独的 0。
保证整个输入文件中不会出现多余的空格。
输出格式
一个整数,表示完成所有杂务所需的最短时间。
输入输出样例
输入 #1复制
7
1 5 0
2 2 1 0
3 3 2 0
4 6 1 0
5 1 2 4 0
6 8 2 4 0
7 4 3 5 6 0输出 #1复制
23【解法】
拓扑排序的过程中,进⾏动态规划。
对于每⼀个事件 ,完成它的最⼩时间为:完成前驱所有事件的最⼩时间中的最⼤值 + 当前事件的完 成时间。因此,可以在拓扑排序的过程中,维护每⼀个事件完成的最⼩时间,然后更新当前事件的最 ⼩时间。
【参考代码】
cpp
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
const int N = 10010; // 杂务数量上限(10000),设10010留余量
int n; // 杂务总数
vector<int> edges[N];// 邻接表:edges[A]存"以A为准备工作的杂务B"(边A→B)
int in[N]; // in[B]:杂务B的准备工作数(入度)
int f[N]; // f[B]:完成杂务B的最早开始时间(等所有准备工作做完)
int len[N]; // len[i]:杂务i的完成耗时
int main()
{
cin >> n; // 输入杂务总数n
// 第一步:读入每个杂务的信息,构建图+统计入度+存耗时
for(int i = 1; i <= n; i++)
{
int b, a;
cin >> b >> len[b]; // b=杂务序号,len[b]=该杂务的耗时
// 读入准备工作,直到遇到0结束
while(cin >> a, a) // 逗号表达式:先读a,再判断a≠0
{
edges[a].push_back(b); // 加边a→b(a是b的准备工作)
in[b]++; // b的入度+1(多一个准备工作)
}
}
// 第二步:拓扑排序初始化------无准备工作的杂务(入度为0)加入队列
queue<int> q;
for(int i = 1; i <= n; i++)
{
if(in[i] == 0) // 没有准备工作,可直接开始
q.push(i);
}
int ret = 0; // 记录所有杂务的最大完成时间(总最短时间)
// 第三步:拓扑排序+动态规划计算完成时间
while(q.size()) // 队列不为空
{
int a = q.front(); // 取出队首杂务a(所有准备工作已完成)
q.pop(); // 弹出队首
// 计算杂务a的完成时间:最早开始时间f[a] + 耗时len[a]
f[a] += len[a];
// 更新总最短时间(取当前最大的完成时间)
ret = max(ret, f[a]);
// 遍历所有以a为准备工作的杂务b(边a→b)
for(auto b : edges[a])
{
// 杂务b的最早开始时间 = 自身当前值 和 a的完成时间的最大值(等a做完才能开始b)
f[b] = max(f[b], f[a]);
in[b]--; // b的入度-1(a的准备工作已完成)
// 如果b的所有准备工作都完成(入度为0),加入队列
if(in[b] == 0)
q.push(b);
}
}
// 输出总最短时间
cout << ret << endl;
return 0;
}