【教程笔记】KalmanFilter

|-------------------------------------------------------|-------------------------------------------------------|--------------------------------------------------------------------------------------------------------|
| 均值 Mean | | 可以使用全量样本的真实值来计算平均值 |
| 期望 Expectation | | 对一个隐藏状态进行足够多次测量以后它所应表现出来的值 |
| 方差 Variance | | 对数据样本在其均值附近散布情况进行的度量 |
| 标准差 Standard Deviation | | 方差的平方根 |
| 正态分布 Normal Distribution （高斯分布 Gaussian Distribution） | | 其函数图像（高斯曲线）又被称为正态分布的概率密度函数 |
| 随机变量 Random Variable | | 可以用来描述系统的隐藏状态。随机变量是一个集合，包含对应的随机试验所有可能的结果取值。随机变量可以是连续的也可以是离散的 |
| k 阶原点矩 | | 是随机变量 kk 次幂的期望 |
| k 阶中心距 | | 随机变量关于均值的散布的 k 次幂的期望 |
[背景知识简介]

补充1：贝塞尔校正

贝塞尔校正（Bessel's correction）是指在样本统计量估计总体参数 时，将样本方差 / 标准差的分母从 n（样本量）替换为 n-1 的修正方法，目的是修正样本方差对总体方差的低估偏差，让样本方差成为总体方差的无偏估计。

样本均值 vs 总体均值

总体方差 公式：（μ 是总体均值，N 是总体数量）

若直接用样本均值替代总体均值计算 "样本方差"

若你已经获取了全部总体数据（如统计一个班级所有学生的成绩方差），无需贝塞尔校正，直接用 N 作分母即可。

只有当数据是 "总体的随机样本"，且需要通过样本推断总体时，才需要用 N−1 校正。

贝塞尔校正仅让样本方差成为总体方差的无偏估计；样本标准差（校正后）仍不是总体标准差的无偏估计（因为平方根是非线性变换），但这是统计学中可接受的近似，且优于未校正的结果。

贝塞尔校正（无偏）公式 ：

示例1 - 给金条称重（状态更新方程）

是一个先验估计：在 n−1 时刻对 n时刻的系统状态所进行的预测

是 n时刻对变量的测量值

是在 n 时刻，使用了 n时刻的测量值，对 X的估计值

是在 n 时刻对未来状态（n+1 时刻）的预测

最后得出的公式为状态更新方程

系数是案例中的情况，在卡尔曼滤波的语境中，这个系数被称作卡尔曼增益，符号为 Kn 其具有下标 n 意味着卡尔曼增益随着每次迭代都会改变。这里还没进入卡尔曼滤波，先写作

这一项被称为"测量残差"，也叫更新量

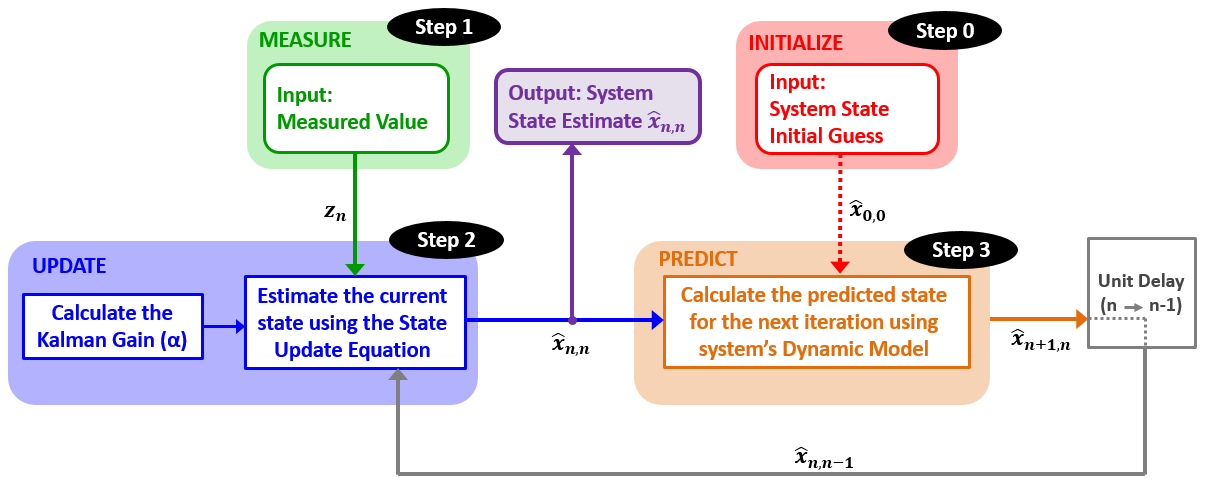
案例所采用的算法如下

| n 时刻 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| | 1 | 1/2 | 1/3 | 1/4 | 1/5 | 1/6 | 1/7 | 1/8 | 1/9 | 1/10 |
| | 996 | 994 | 1021 | 1000 | 1002 | 1010 | 983 | 971 | 993 | 1023 |
| | 996 | 995 | 1003.67 | 1002.75 | 1002.6 | 1003.83 | 1000.86 | 997.125 | 996.67 | 999.3 |

	996	995	1003.67	1002.75	1002.6	1003.83	1000.86	997.125	996.67	999.3

按照时间运行出来的数据如上表所示，给金条称重的案例使设计了一个针对静态系统的简单估计算法。我们还推导出了五个卡尔曼滤波方程之一的状态更新方程

示例2 - 跟踪直线匀速运动的飞行器（状态转移方程）

是时候考虑一下状态随时间变化的动态系统了。本例中，我们尝试用 α−β 滤波器对一个直线匀速飞行中的飞行器进行跟踪。

假设一个只有一个维度的世界中，有这样一个飞行器在往远离雷达的方向飞行（或者靠近雷达）。因为是一维空间，飞行器到雷达的角度是恒定的，其高度也是恒定的。

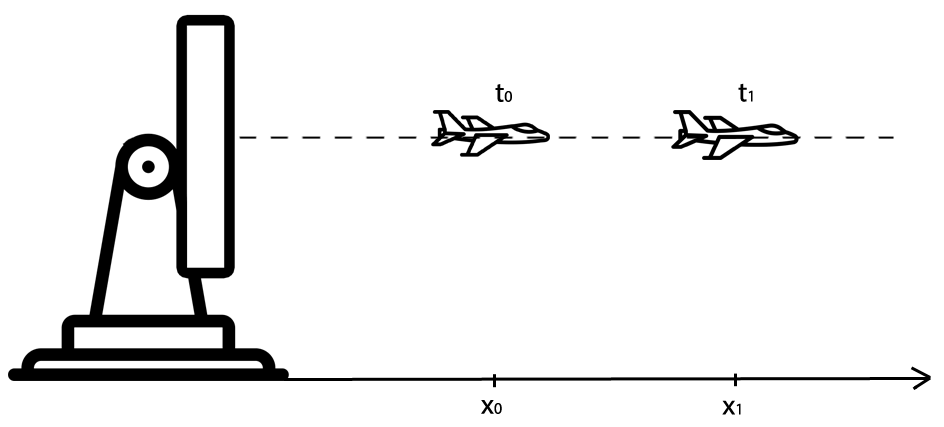
xn 表示 n时刻飞行器的距离。下一个采样周期时的飞行器距离等于当前飞行器距离加上目标速度乘以采样间隔时间。由于我们假设飞行器的速度不变，下一时刻的速度等于当前时刻的速度。雷达向目标的方向以固定频率发射跟踪波束，两次跟踪测量之间的时间间隔为 Δt

有以下公式：

速度是距离的导数:

|----------|-------------------------------------------------------------------------------------------------------|
| 下一时刻的距离： | |
| 下一时刻的速度： | ，也可写成 |

上述方程称为 状态外插方程 (也叫转移方程或预测方程)。

下面再看雷达跟踪问题的状态更新方程，这又叫α−β 跟踪更新方程或 α−β 跟踪滤波方程。

|-------------|-------------------------------------------------------------------------------------------------------------------------------------------------|
| 位置的状态更新方程为： | |
| 速度的状态更新方程为： | |

注：本例中，我们是根据雷达距离测量来间接估计的飞行器速度的

估计算法如下图

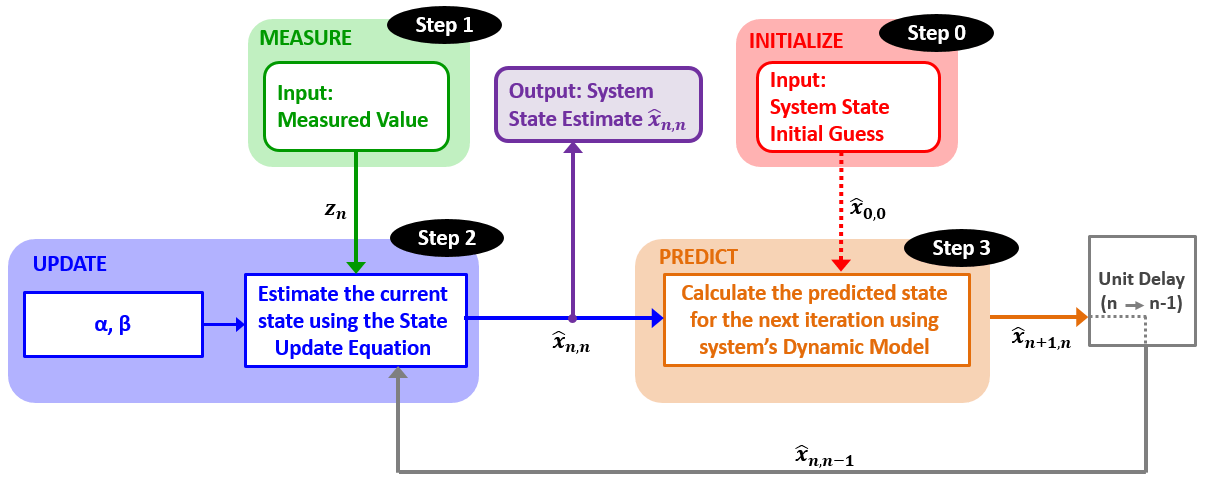
一维卡尔曼滤波

如之前所言，卡尔曼滤波基于五个方程，我们已经见过了其中的两个：

状态更新方程
动态模型方程

本章我们推导其余三个卡尔曼滤波方程，并重新审视状态更新方程。

1.过程噪声

真实世界中，系统动力模型总是有不确定性的。比如我们想测量一个电阻的阻值，我们假设它是不变的，即阻值不随测量过程而改变。但实际上阻值会随着环境温度的改变而轻微改变。再比如用雷达追踪弹道导弹时，导弹动态模型的不确定性会包含一些随机的加减速。对于飞行器之类的目标，模型不确定性更大，因为飞行员随时可能进行机动。

另一方面，当我们用GPS接收机计算一个固定物体的位置时，由于固定物体不会动所以动态模型不确定性为0. 动态模型的不确定性称为过程噪声。一些文献中也叫模型噪声、驱动噪声、动态噪声或系统噪声。过程噪声也会带来估计误差。

上一个例子里，我们估计了大楼的高度。由于大楼高度客观上不会改变，我们没有考虑过程噪声。

过程噪声方差用 q表示。协方差外插方程应包含过程噪声方差。

恒定动态模型的协方差外插方程为：

2.一维卡尔曼滤波完整模型

下表总结了五个卡尔曼滤波方程：

	方程	方程名
状态更新阶段		卡尔曼增益 Kalman Gain
状态更新阶段		状态更新 State Update
状态更新阶段		协方差更新 Covariance Update
状态预测阶段	(恒定动态模型) (速度恒定动态模型)	状态外插 State Extrapolation
状态预测阶段

**注1：**状态外插方程和协方差外插方程依赖具体系统的动力学模型。

**注2：**上表所描述的卡尔曼滤波方程是针对特定问题的特定形式。其一般形式在后续会以矩阵形式给出。目前我们意在理解卡尔曼滤波的基本原理和概念。

|----------|------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
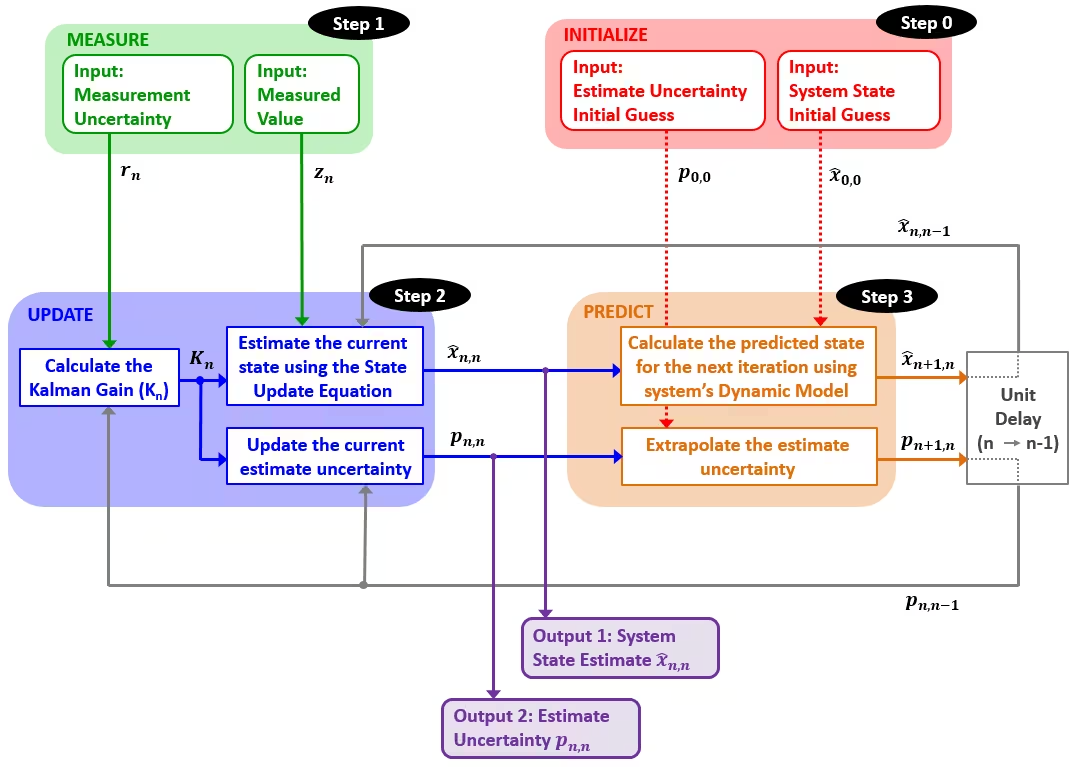
| 第0步：初始化 | * 初始状态 * 初始状态方差 |
| 第1步：测量 | * 测量值 * 测量方差 |
| 第2步：状态更新 | 状态更新过程给出当前系统状态的估计。状态更新过程的输入为： * 测量值 * 测量方差 * 状态预测 * 状态预测方差基于这些输入，状态更新过程计算卡尔曼增益并产生输出： * 状态估计 * 状态估计方差 |
| 第3步：预测 | 预测过程使用系统动态模型将当前系统的状态估计及其方差外插到下一个时刻。第一次迭代时，初始化参数被当作状态预测的值和方差。预测的输出被当作下一个时刻的状态预测的值和方差。 |

3.对卡尔曼增益的理解

把状态更新方程等效变换一下：

可见，卡尔曼增益是测量的权重，这一项则为当前状态预测的权重。

低卡尔曼增益

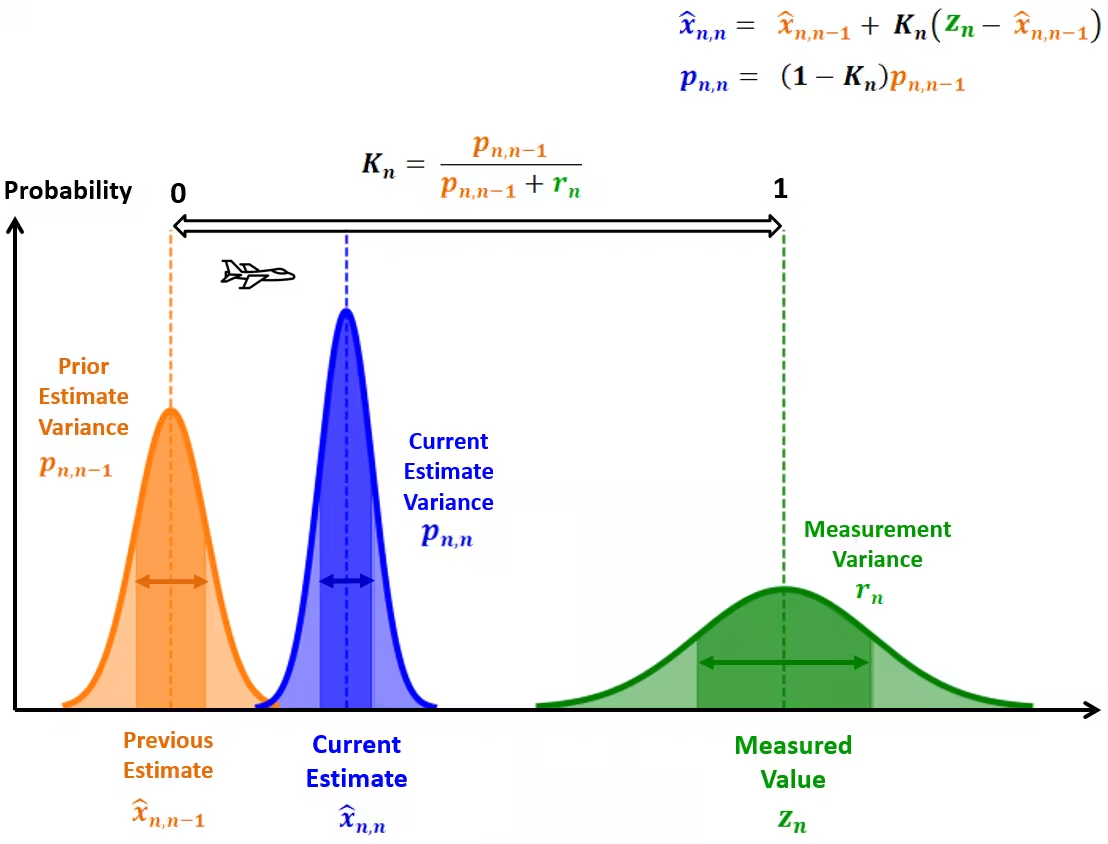
高卡尔曼增益

4.滞后误差

案例中之所以产生滞后误差，有两个原因：

动态模型和实际不符。
我们设定了过低的过程噪声 (q=0.0001)(q=0.0001)，而真实的温度变化要远大于这个值。

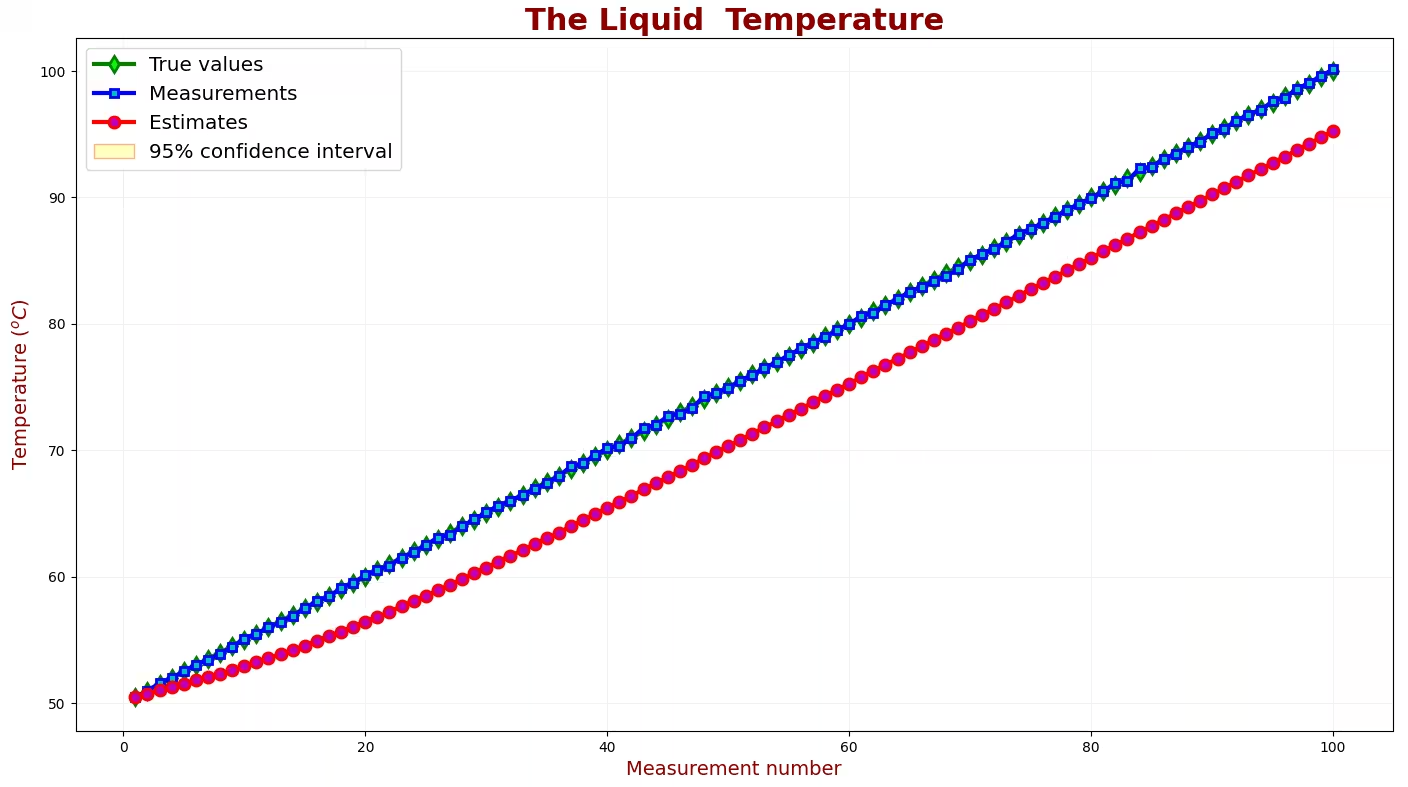
有两个方法能消除滞后误差：

其一，如果我们能预先知道液体温度是线性变化的，就可以设计一个考虑温度线性增长的动态模型。在示例 4中我们就是这样做的，也是一般情况下推荐采用的方法。但是如果温度变化的规律没办法建模，那这种手段就不能改善卡尔曼滤波的性能。
其二，既然是模型失准了，我们可以把模型差异当作一种噪声，可以提高模型的过程噪声 (q)(q)，下一个示例会具体讲这种方法。

第二部分：多变量卡尔曼滤波（矩阵形式）

线性卡尔曼滤波（LKF），LKF假设系统动态模型是线性的。

截至目前，我们已经处理过一维问题，例如估计液体温度。但是许多动态过程有2、3甚至更多个维度。比如，用于描述在三维空间中运行的飞机的位置的状态向量：

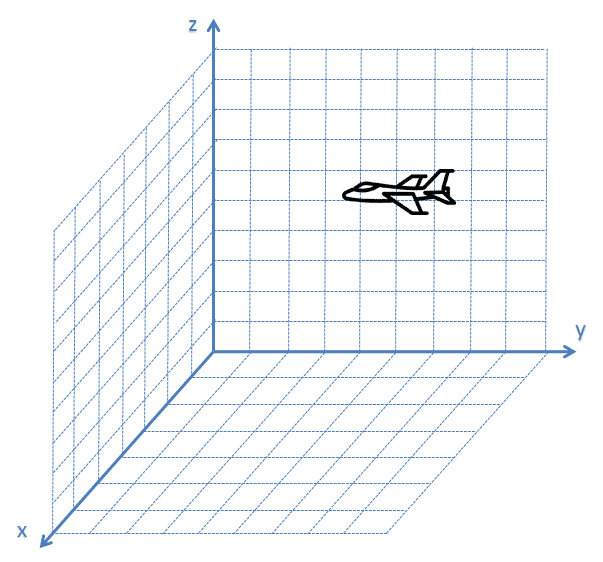
背景知识

需要了解这些背景知识

矩阵运算
期望的代数运算
多变量正态分布

具体需要了解的知识总结为如下表格：

|---------|----------------------------------------------------------------------------------------------------|
| 矩阵运算 | * 向量和矩阵的加法和乘法 * 矩阵转置 * 逆矩阵（不需要知道怎么求逆，只需要知道逆矩阵是什么即可） * 对称矩阵 * 特征值和特征向量重点关注：点乘和叉乘，各个运算的物理含义 |
| 期望的代数运算 | * 基本期望代数运算法则 * 方差和协方差的期望的代数运算法则要点：协方差衡量两个随机变量的线性相关程度，工程场景IMU 的三轴噪声若相互独立，则两两协方差为 0，协方差矩阵为对角矩阵。 |
| 多变量正态分布 | * 双变量正态分布 * 置信区间 * 协方差椭圆 * 置信椭圆 |

状态外插方程

也叫状态转移方程

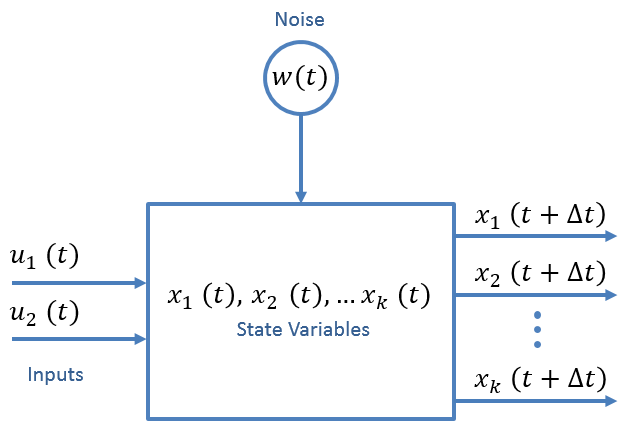
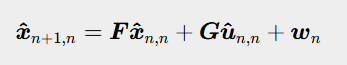
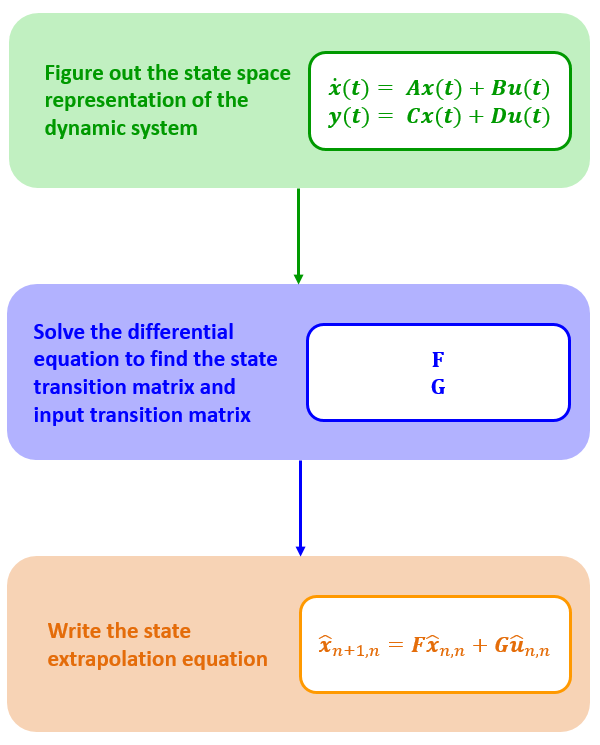
线性动态系统建模

建模的目的是推导出如下状态外插方程

为达到这个目的，我们需要对动态系统进行建模。也就是说，思考出动态系统的状态空间表达。下面两个方程就是LTI系统的状态空间表达：

其中：x-状态向量，y-输出向量，A-动态矩阵，B-输入矩阵，C-输出矩阵，D-前馈矩阵

这部分有对高阶动态系统建模的推导，在此处略去。

目标是找到 状态转移矩阵 F，需要求解微分方程来获取 F

有输入u（t）的情况要加上

协方差外插方程

本节中，我们将推导卡尔曼滤波的协方差外插方程（或协方差预测器方程）的矩阵形式。

其中：

是当前状态估计的不确定性的平方（协方差矩阵）

是下一个状态预测的不确定性的平方（协方差矩阵）

F是在"线性动态系统建模"一节推导的状态转移矩阵

Q是过程噪声矩阵

在状态转移方程中，是n时刻的过程噪声，在一维卡尔曼滤波中，过程噪声方差记为 q；在多维情况下，过程噪声是一个协方差矩阵，记为 Q

过程噪声方差对卡尔曼滤波性能有非常大的影响，过小的 q会造成滞后误差；而如果 q的值过高，卡尔曼滤波会完全相信测量值，造成估计值噪声过大。

环境过程噪声有两种模型：

离散噪声模型：

假设噪声在每个采样点是不同的，但是在采样点之间是相同的（零阶保持）。用期望的运算法则即可得出协方差矩阵。

连续噪声模型：

快速构建Q矩阵的方式：

1.状态转移矩阵投影法

如果动态模型不包含输入，我们可以用状态转移矩阵把加速度的方差投影到我们的动态模型中

先定义

过程噪声矩阵为：

2.输入转移矩阵投影法

如果动态模型包含输入，我们可以更快捷地算出 Q矩阵

式中 G是控制矩阵（或输入转移矩阵）。

测量方程

现在开始，我们将讲述当前时刻的算法。先从测量方程开始。

在"一维卡尔曼滤波"一章中，我们把测量值记为

测量值表示一个真实系统状态值和测量设备引入的随机测量噪声的叠加。

矩阵形式的一般情况测量方程如下：

H是观测矩阵：在许多场景中，测量值不是希望获取的系统状态，观测矩阵 H的意义就是以线性变换的形式，将系统状态变换到测量输出。

中期小结

卡尔曼滤波有五个关键方程。

两个预测方程：

++状态外插方程++ - 基于当前的估计来预测或估计未来的状态
++协方差外插方程++ - 上述未来的状态估计的不确定性

两个更新方程：

++状态更新方程++ - 基于上一时刻的预测和当前的测量来估计当前的状态
++协方差更新方程++ - 当前状态估计的不确定性。

++卡尔曼增益方程++ - 两个更新方程中会用到。卡尔曼增益是个测量值和预测值之间的"权重系数"，它表明了应该相信多少过去的预测值，又应该相信当前的测量值。

目前，我们已经学习了矩阵形式下的两个预测方程，以及计算它们所需的几个辅助方程。

|--------------|---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 预测方程（状态外插方程） | |
| 协方差外插方程 | |
| 测量方程 | |
| 协方差方程 | |
| 测量协方差 | |
| 过程噪声协方差 | |
| 估计协方差 | |

更新方程

|-------------|-----------------------------------------------------------------------------------------------------------------------|
| 状态更新方程 | |
| 协方差更新方程（简化） | |

卡尔曼滤波的全部方程

|--------|-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|---------|
| | 方程 | 方程名 |
| 预测 | | 状态外插 |
| 预测 | | 协方差外插 |
| 更新（修正） | | 状态更新 |
| 更新（修正） | | 协方差更新 |
| 更新（修正） | | 卡尔曼增益 |
| 辅助方程 | | 测量方程 |
| 辅助方程 | | 测量协方差 |
| 辅助方程 | | 过程噪声协方差 |
| 辅助方程 | | 估计协方差 |