
🎈主页传送门****:良木生香
🌟人为善,福随未至,祸已远行;人为恶,祸虽未至,福已远离
上期回顾:在上一篇文章中(【数据结构-初阶】二叉树(1)---树的相关概念),我们学习了树的相关概念,知道了什么是树,树的基本术语有哪些,以及树在我们生活中的具体应用,那么现在我们就来继续学习树的一种类型---二叉树.
目录
一、二叉树的概念:
在树形结构中,我们最常用的就是二叉树。二叉树,顾名思义就是一个结点下分出两个枝杈的树形结构。一颗二叉树是节点的一个有限集合,该节点由一个根节点加上两棵分别称为左子树和右子树的二叉树组成或者为空。下面是二叉树的树形结构图:
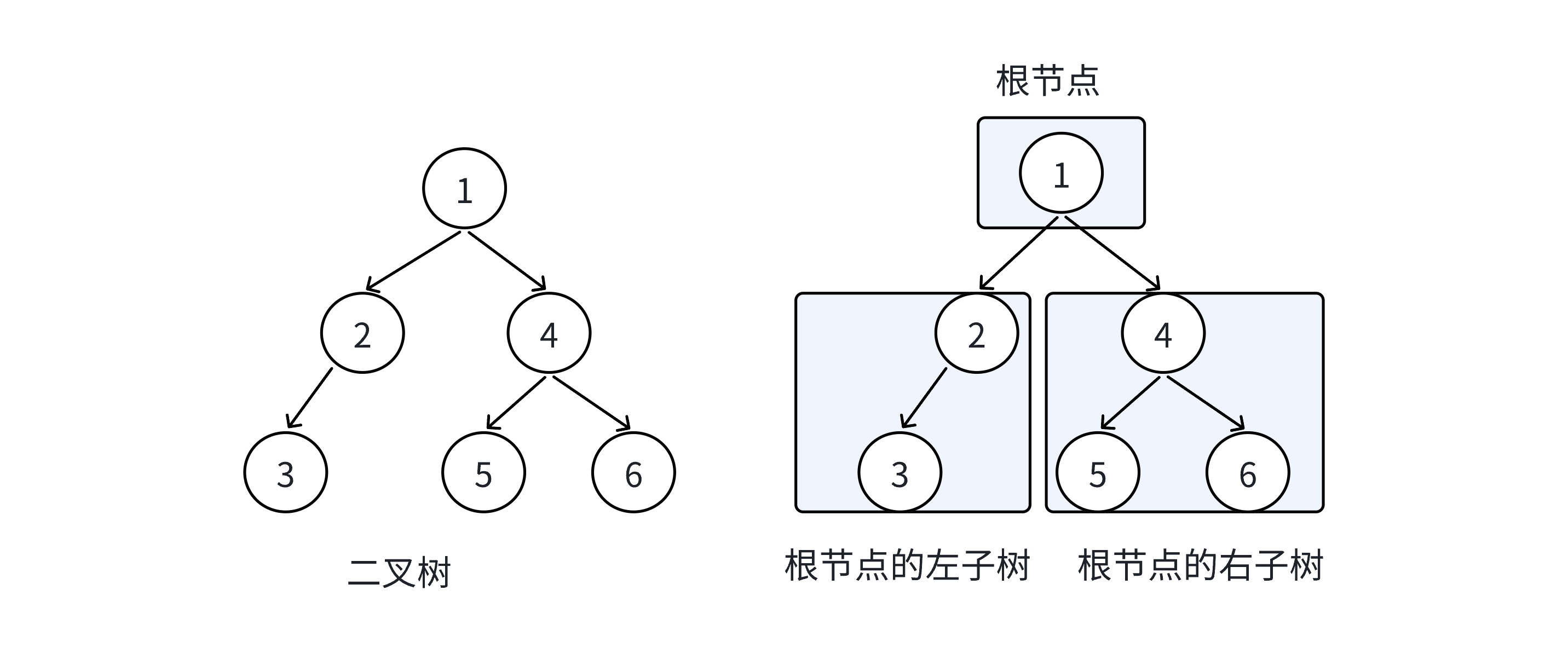
从上面两张图中我们可以看出二叉树具有以下特点:
- 二叉树不存在度大于2的结点
- 二叉树有左右子树之分,次序不能颠倒,因此二叉树是有序树二叉树
不管二叉树是什么样的结构形状,他们都是由下面这几种情况复合而成的:
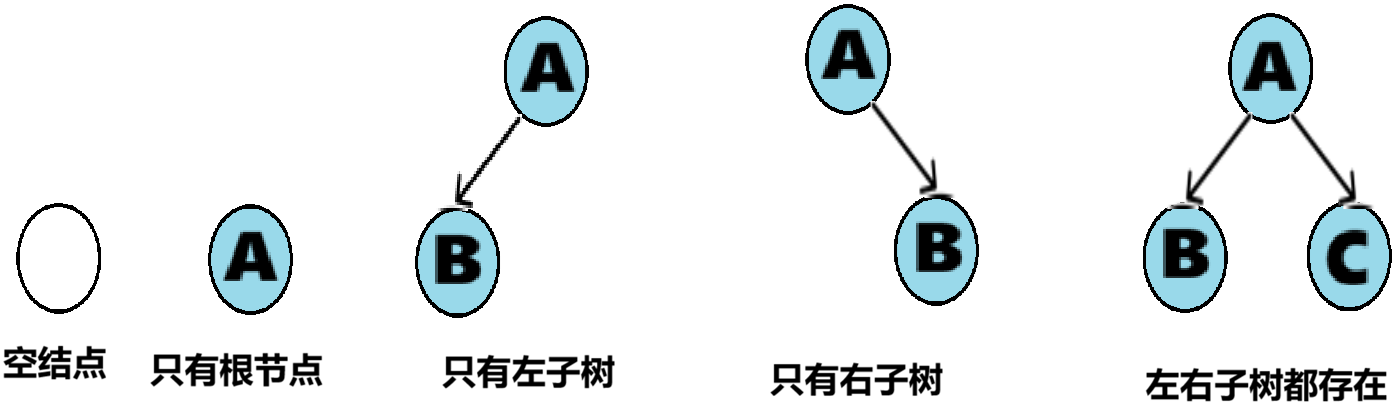
二、特殊二叉树
2.1、满二叉树
满二叉树,顾名思义就是除了叶子结点之外,其他节点都由两个子树,简单来说,就是每一层的结点个数都达到了最大值。对于满二叉树,有这样的一个性质:假设这颗二叉树有k层,那么****每一层的结点个数就是2^(k-1),总结点个数就是2^k-1
相反的,如果这棵树有k层,总结点个数是2^k-1,那么这棵树就可以判定为二叉树
下面是满二叉树的树形结构图:
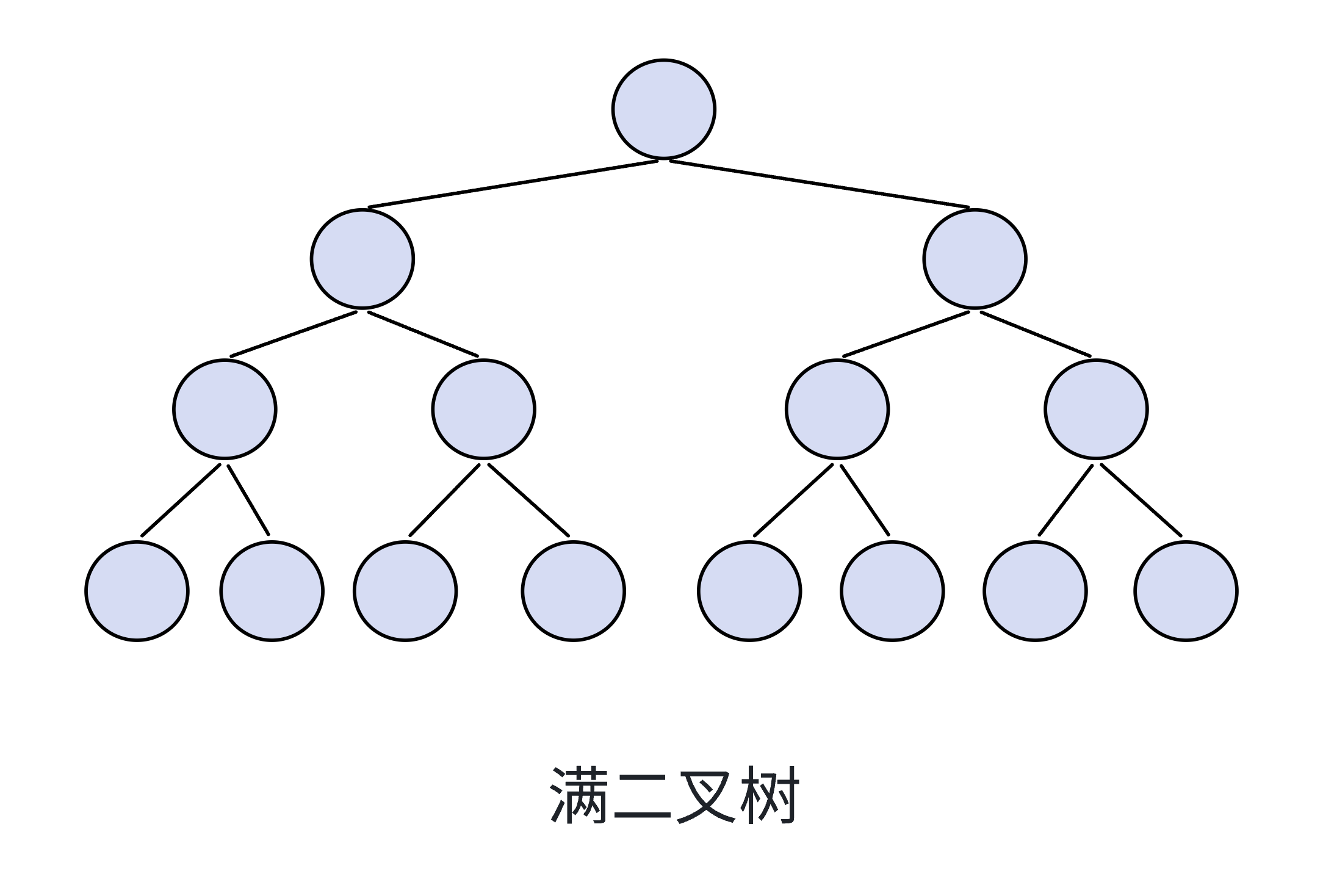
2.2、完全二叉树
完全二叉树是一种效率很高的二叉树,它是由满二叉树引出来的。
我们将深度为k,有n个结点的二叉树,当且仅当其每一个结点斗鱼深度为k的满二叉树中编号从1到n结点一一对应时称之为完全二叉树.
小贴士:满二叉树是一种特殊的完全二叉树
下面是完全二叉树的树形结构图:
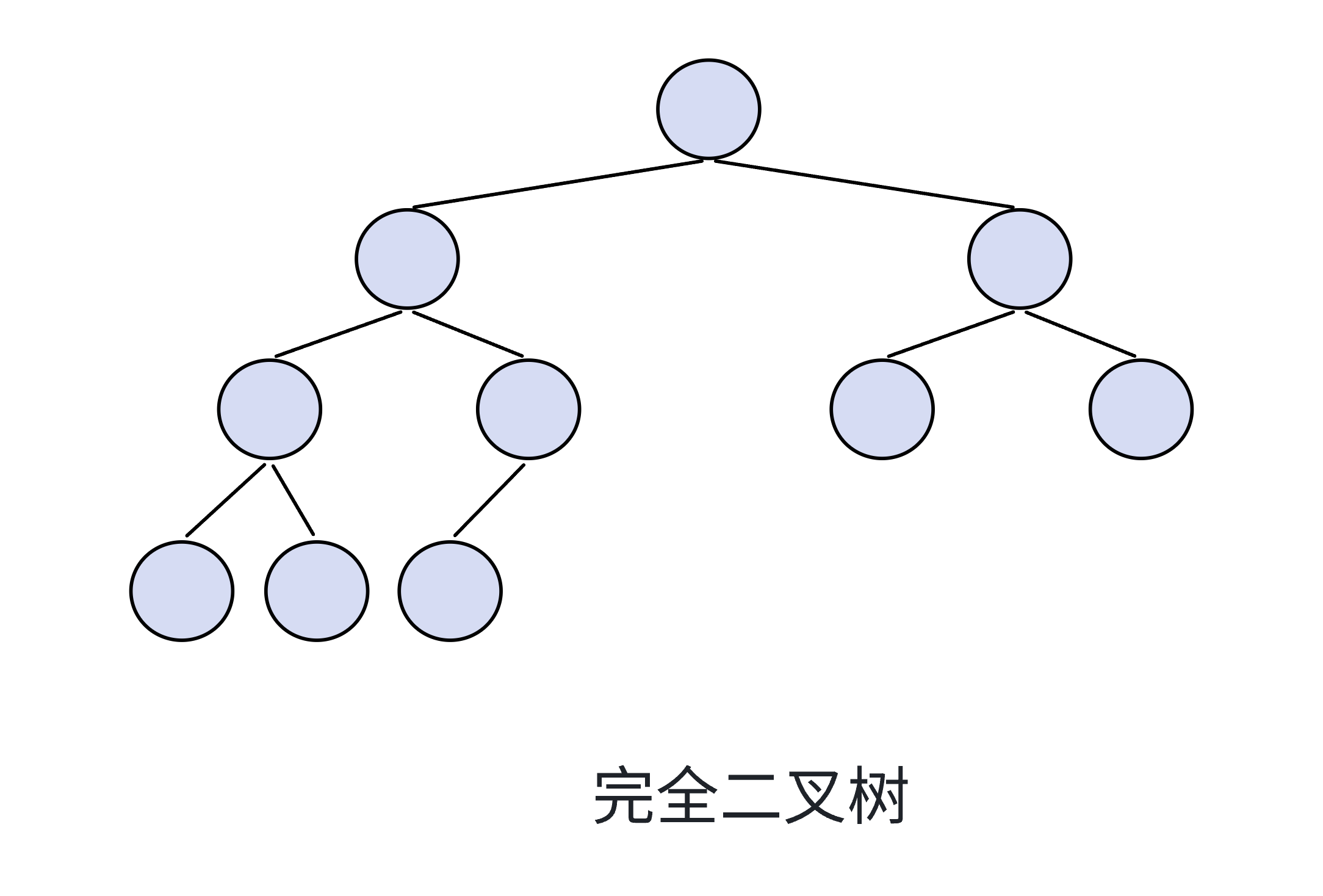
也就是说,在完全二叉树中,我们在最后一层上不一定都要有叶子结点,但是除了最后一层,其他层都必须是满的结点,如果完全二叉树的所有结点都是满的,那这棵完全二叉树就是满二叉树
二叉树的性质:
- 若规定根结点的层数为 1 ,则⼀棵⾮空⼆叉树的第i层上最多有 2^(i-1) 个结点
- 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是2^h-1
- 如果规定的根结点的层数是1,具有n个结点的满二叉树的深度h=log2(n+1)[就是log为以2为底,n+1为对数]
以上就是特殊二叉树的概念与基本性质的讲解了
2.3、其他的二叉树
在二叉树的分类中,除了上面讲的满二叉树和完全二叉树之外,还有平衡二叉树,二叉搜索树,左/右斜二叉树,红黑树,哈夫曼树等等
三、二叉树的存储结构
在线性表的学习中,我们知道,存储结构分为顺序存储和链式存储,在二叉树中,也分为顺序存储和练市存储两种存储方式
3.1、顺序存储
顺序存储就是用数组来存储数据,那我们来回顾一下在之前的学习中有哪些线性表是使用了顺序存储的呢?那就是顺序表和栈了,这两种顺序表是以数组为基础的数据结构。那么在二叉树中也可以用****顺序存储的方式存储数据
一般来说在二叉树中,用数组存储数据会更加适合表示完全二叉树,因为不是完全二叉树的话会造成空间的浪费,完全二叉树会更加适合用顺序结构存储.向我们之前说的,完全二叉树的是有序的,先到根节点,再到左右节点,所以在数组中能更好的确定每个元素的位置 ,如下图所示:
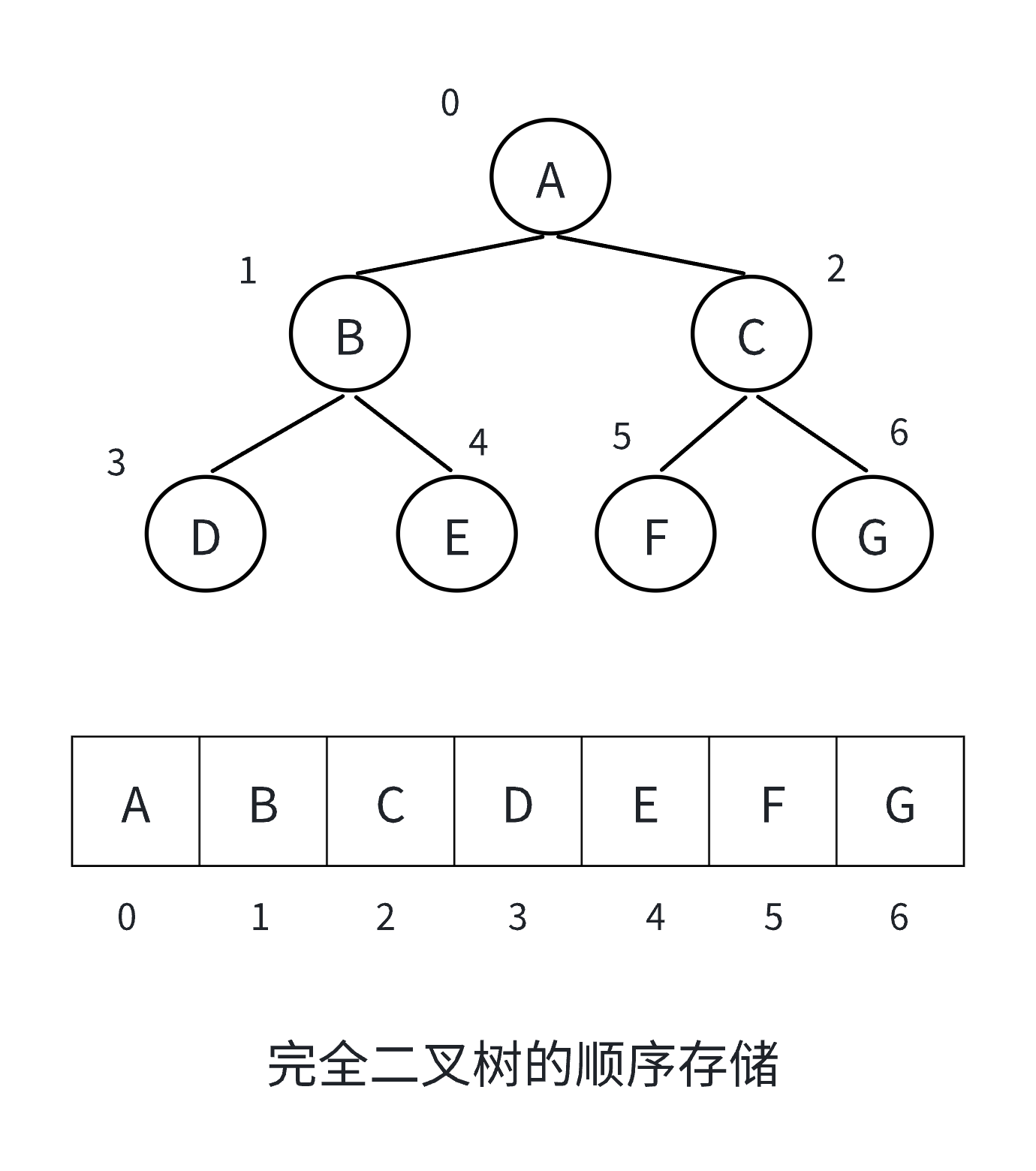
根节点毫无疑问就是在数组的第一个位置,随后是根节点的左子树,再到右子树,再到左子树的左节点右节点...以此类推,这样每个节点在数组中都有一一对应的位置,这是完全二叉树在数组中的存储结构,那如果不是完全二叉树呢?在数组中又该怎么表示呢?简单,如下图所示:
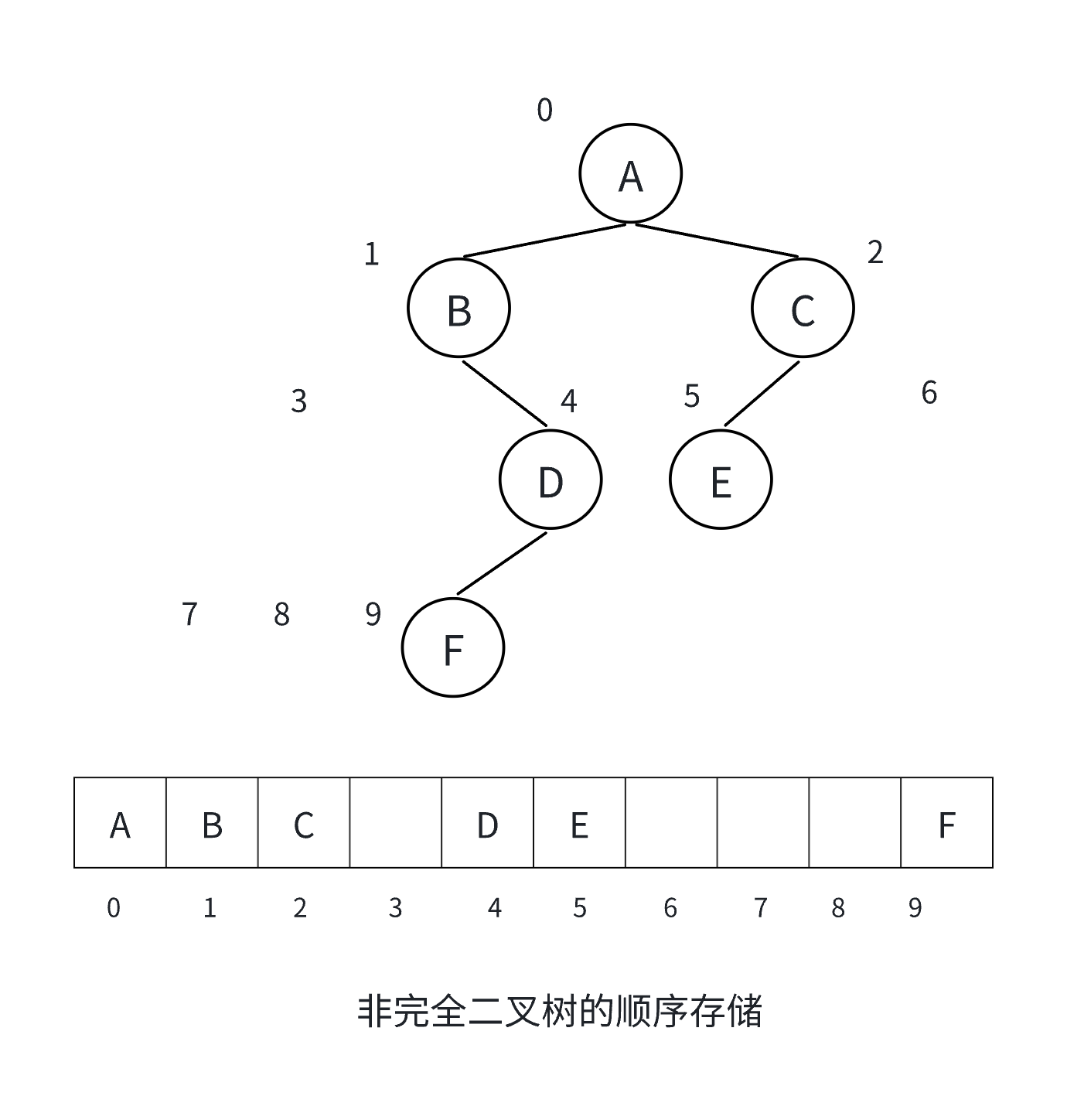
依旧是像完全二叉树那样,每个节点都呆在自己的专属位置上,因为二叉树在理论上每一层的结点个数是固定的,所以每个节点在数组中存储的位置也是固定的,即使这个节点没有兄弟节点.
小贴士:在现实中,我们通常将堆(一种二叉树)使用顺序结构的数组来存储结构,需要注意的是我们在这里说的堆和操作系统中的虚拟进程地址空间的堆事两回事,虽然名字一样,但是作用却大不相同,一个是顺序结构,一个是操作系统中管理内存的一块区域分段
3.2、链式存储
说完了顺序存储,现在我们来讲讲链式存储。二叉树的链式存储结构是指用链表来表示一颗二叉树,即用链表来表示二叉树元素的逻辑关系
用链表表示二叉树通常的方法是每个链表节点中有三个作用域组成,分别是左右指针域和数据域,左右指针域存储的是该结点的左右孩子的地址,数据域是该节点存储的数据,这就是我们现在要学习的二叉链表。在二叉树的链式表示中,分为刚刚讲的二叉链表,还有三叉链表,这会在c++课程中详解讲解,大家敬请期待哈.三叉链表就是指针域有三个指针,除去指向左右孩子的指针外,还多出一个指向父结点的指针,这一般会在红黑树等高阶数据结构中会使用到,下面是这两种链表的结构图:
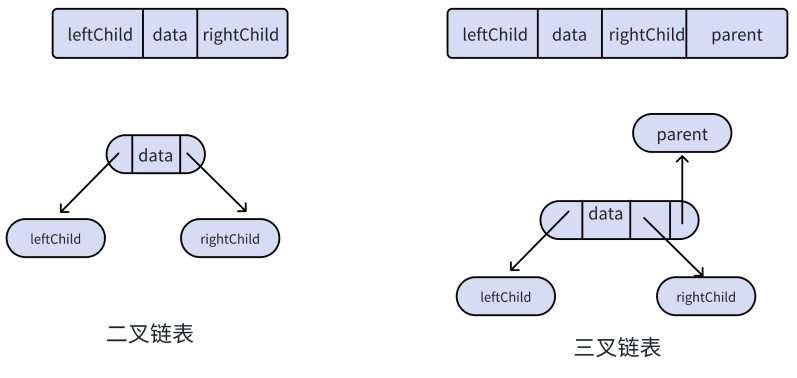
对应上二叉树的结构就是下图所示的内容:
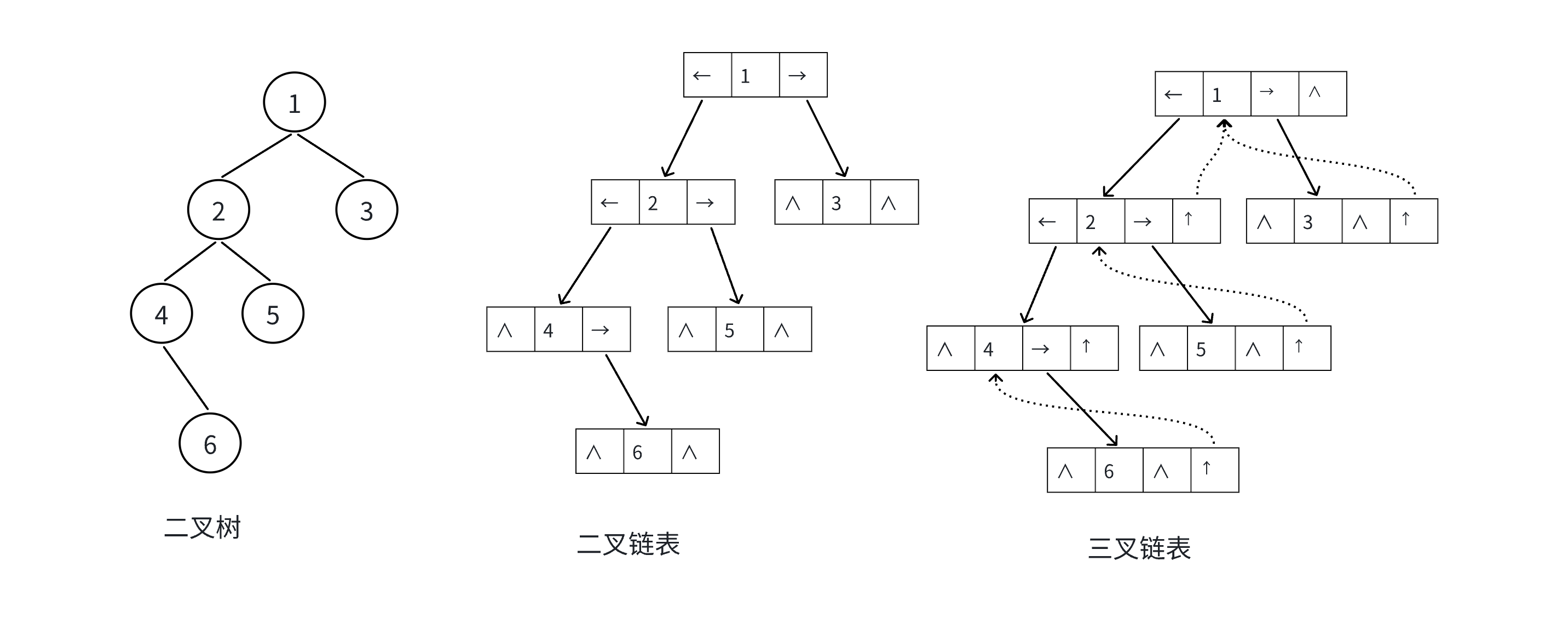
以上就是二叉树存储结构的详解了.
四、顺序结构二叉树实现
想要实现二叉树的顺序结构,我们该从哪个方面入手呢?换句话说,我们应该用什么样的数据来体现顺序结构二叉树的性质呢?有一个好方法:用堆。为什么呢?因为堆是一种特殊结构的二叉树,在具备二叉树的性质的同时,还具备其他可以学习的性质
4.1、堆的概念与结构
堆的概念:
如果有⼀个关键码的集合 K= {k0 , k1 , k2 , ...,*kn*−1 } ,把它的所有元素按完全⼆叉树的顺序存储⽅式存储,在⼀个⼀维数组中,并满⾜: Ki<= K2∗i+1 ( K**i>= K2∗i+1 且 K**i<= K2∗i+2 ), i = 0、1、2... ,则称为⼩堆(或⼤堆)。将根结点最⼤的堆叫做最⼤堆或⼤根堆,根结点最⼩的堆**
叫做最⼩堆或⼩根堆。
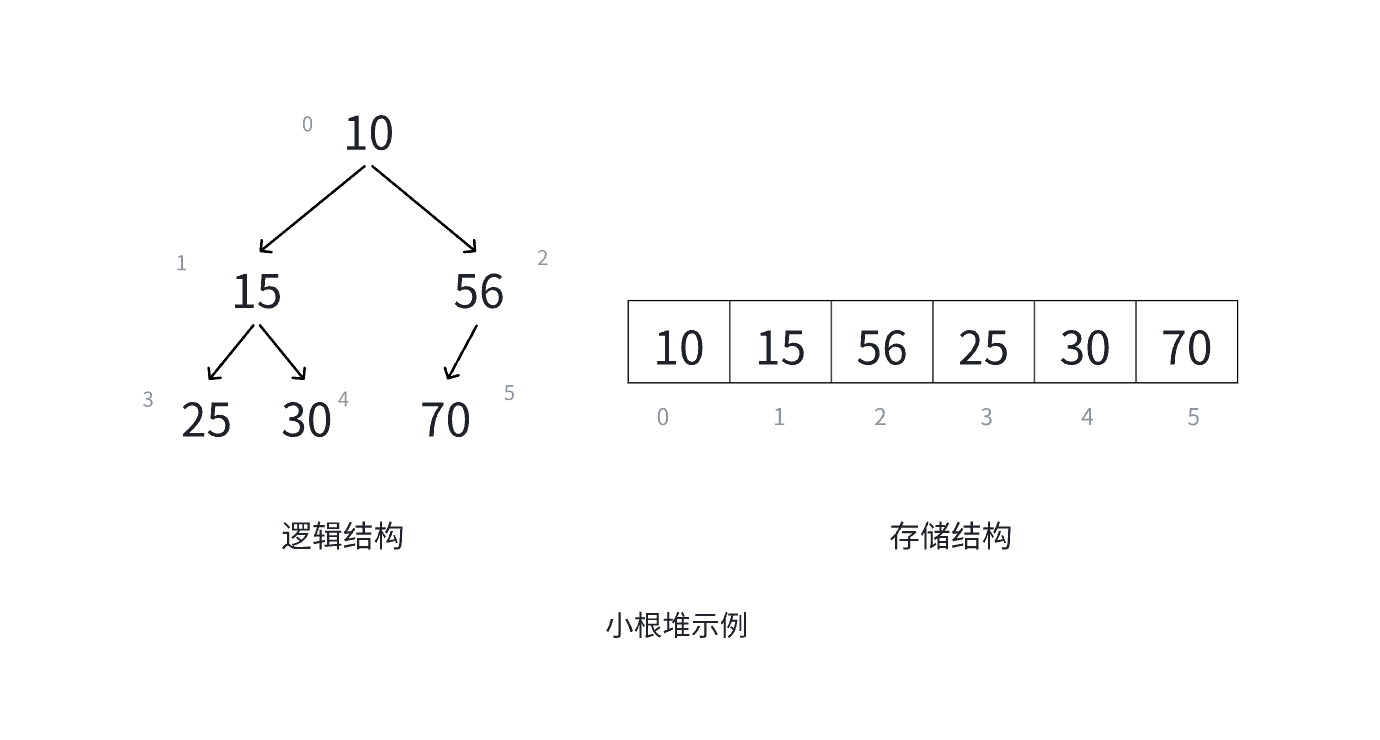
也就是说, 父结点存储的数据都比子节点存储的数据大,那就是大根堆,父结点存储的数据都比子节点存储的数据小,那就是小根堆
下面是大小根堆的图示以及在数组中存储的方式:
小根堆:
大根堆:
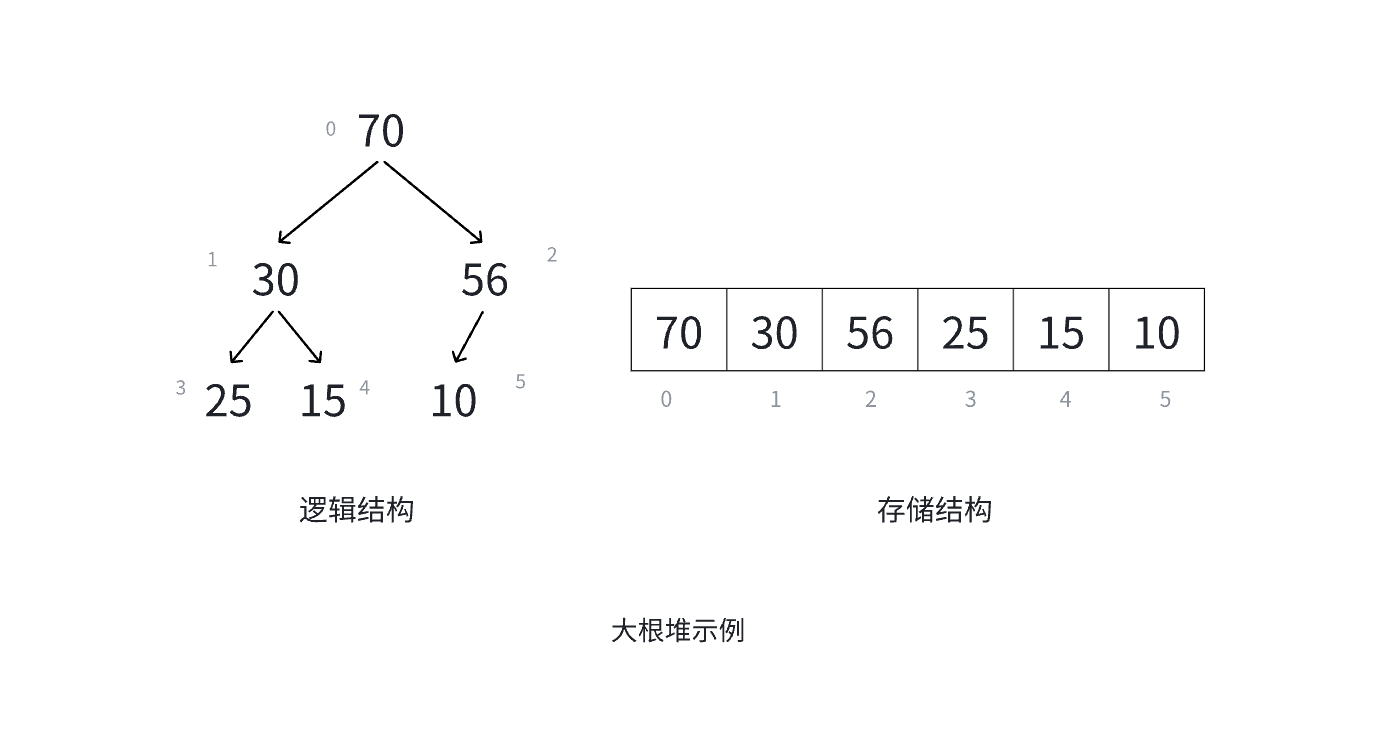
堆的性质:
- 堆中某个结点的值总是不大于或者不小于父结点的值
- 堆总是一棵完全二叉树
4.2、顺序结构二叉树的性质
由此可以推出,顺序结构的二叉树具有以下性质:
- 对于具有n个结点的完全二叉树,如果按照从上到下,从左到右的数组顺序对所有结点从0开始编号,则对于编号为i的节点有以下性质:
- 若i>0,i位置结点的双亲序号(父结点序号);****(i-1)/2;i=0,则i为根结点编号,无父结点
- 若2*i+1<n,左孩子编号为:2*i+1;2*i+1>=n则没有左孩子;
- 若2*i+2<n,右孩子编号为:2*i+2;2*i+2>=n则没有右孩子;
4.3、堆的实现
堆的实现我们依旧从增、删、查、改四个方面进行学习。
4.3.1、堆的结构与初始化
我们知道,堆的底层是数组,那么堆的结构就应该是:
cpp
//二叉树的顺序存储本质上就是数组,类似线性表,所以结构体与线性表相同
typedef struct Heap {
Elemtype* arr;
int size; //当前二叉树中有效的元素个数
int length; //当前二叉树中的总容量
}Heap; //重命名为heap看起来是不是似曾相识?那就对了,这个结构与顺序表的不能说非常相似,可以说是一模一样,既然结构式这样的,那初始化的方法是不是也一样?是的,就是一样的:
cpp
//对堆进行初始化
void Init_Heap(Heap* pHeap) {
pHeap->arr = NULL;
pHeap->size = pHeap->length = 0;
}4.3.2、入堆(堆的插入)
堆的插入如就有点说法了,堆是一种二叉树,也可以当做一个数组,那么我们插入数据是插入在那个位置呢?从数组的角度来讲,我们可以在头部,尾部,pos位置进行插入,但是从二叉树的角度来讲,头部和pos位置是不是已经固定了?假设你在头部或者pos位置插入,那二叉树是要重新给你分配一个新结点还是把原来的元素挤掉?都不合理,所以从二叉树的角度来讲,我们选择在二叉树的末尾进行元素的插入,也就是数组的尾部插入
假设我们现在还有一棵二叉树长这样:
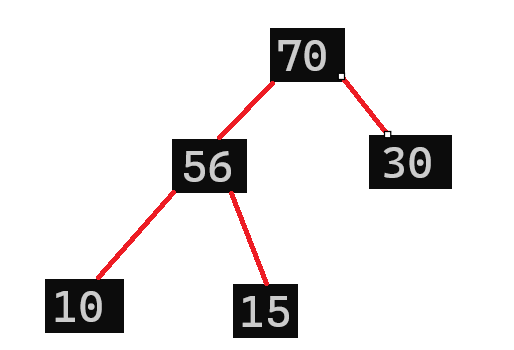
我现在想在这棵二叉树后面插入一个数字:80,我们知道,是放在这棵树的末尾,那哪里是末尾?是15还是10还是30的子结点?根据我们对于二叉树的理解,他是一棵有序二叉树,那么末尾,也就是当前末尾节点的下一个节点就应该是30的左节点,那么下面就是插入之后的图片:
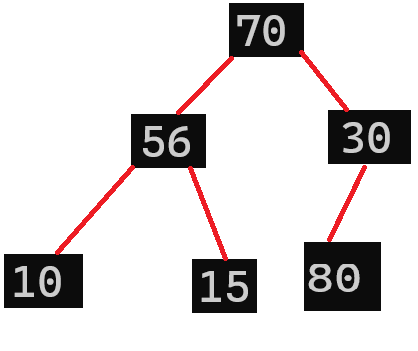
但是通过观察,我们这棵二叉树本应该是大根堆的二叉树,在加入80之后,就破坏了这棵二叉树原有的性质了,想要让它重新回到大根堆的性质我们该怎么办?那就是移动80这个元素,移动到这棵二叉树重新回到大根堆的性质为止.
大根堆是父结点存储的值都比其子节点大,那我们就让80向上移动,我们把80向上移动的这个过程叫做****向上调整算法
4.3.2.1、向上调整算法
这个算法的思路就是,将最后一个节点与其父结点相比较,如果其值大于其父结点,那就与父结点交换,再继续与交换后的新父节点比较,如果还大于父结点,那就继续交换,继续往上走,直到满足大根堆的性质为止:
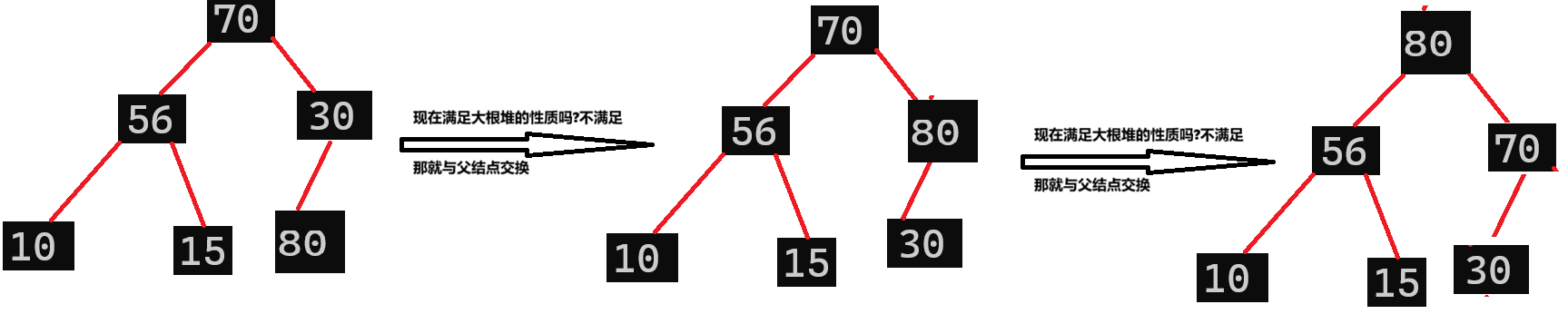
当80到达世界最高点时,那就算是比所有子节点都要大了,这样就完成了向上调整算法的整个过程,下面是代码:
cpp
//现在是向上调整算法(大顶堆):
void adjustUP(Elemtype* arr, int child) {
int parent = (child - 1) / 2;
while (child > 0) {
//对于下面if语句里面的大小比较:
//大根堆:<
//小根堆:>
if (*(arr+parent) < *(arr+child)) {
Swap(arr+parent, arr+child);
child = parent;
parent = (child - 1) / 2;
}
else {
break;
}
}
}所以大根堆的整个插入代码就是:
cpp
//堆的插入(大顶堆)
void Push_Heap(Heap* pHeap, Elemtype data) {
//插入是插入在末尾的
//空间不够,增容
if (pHeap->size == pHeap->length) {
//为总容量扩容
int newLength = pHeap->length == 0 ? 4 : 2 * pHeap->length;
//为arr申请一块新的空间
Elemtype* newbase = (Elemtype*)realloc(pHeap->arr, newLength * sizeof(Elemtype));
if (newbase == NULL) {
perror("内存申请失败:");
return;
}
pHeap->arr = newbase;
pHeap->length = newLength;
}
//空间足够:
pHeap->arr[pHeap->size] = data;
//插入之后要用到向上调整算法
adjustUP(pHeap->arr,pHeap->size);
pHeap->size++;
}在这段代码中,步骤都与线性表的大差不差,都是判空,申请空间,插入.
小贴士:如果是小根堆的插入,那也是把元素往上调整,看看父节点是不是比他大,如果是,那就向上调整,保证小根堆的父节点的值都要比子节点的值要大,所以我们只用修改代码中的大于号就实现了小根堆的向上调整代码,在上面的代码中已经注释上了.
那么这就是堆的插入了.
4.3.3、出堆(堆的删除)
**堆的删除要考虑的问题与插入一样,删除数据要删除哪个位置.为了保证堆顶结构在删除的时候不会崩溃,我们规定,删除堆顶元素(即删除最值).**在这里要说的是,我们对堆的所有操作都是围绕堆顶元素展开的,就算没有直接操作的也有间接操作,这就是为了不让堆结构不崩塌.
现在要考虑第二个问题:删除堆顶元素,是直接删除吗?像下面这样?
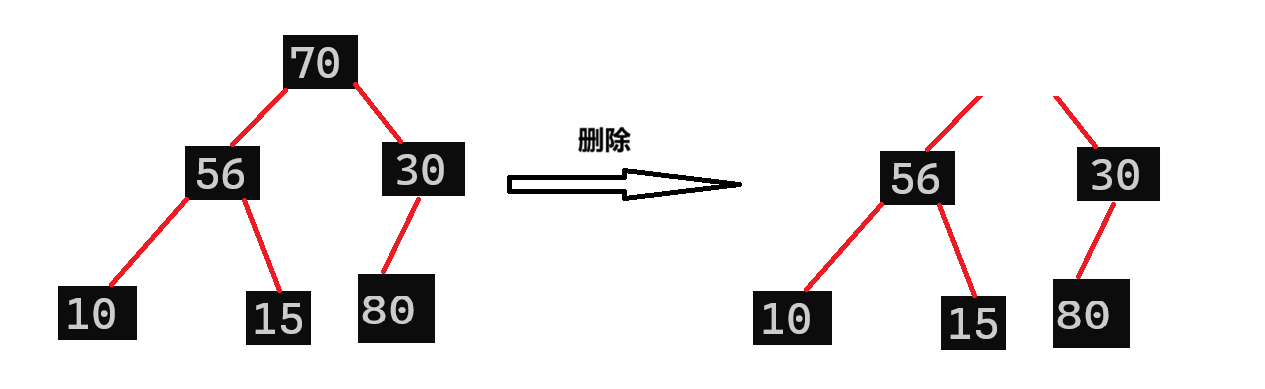
很显然,肯定不是嘛,这样删除就直接破坏了堆的结构了,那该怎么办呢?有个好方法,我们可以将对顶元素与堆底元素进行交换,如下图所示:
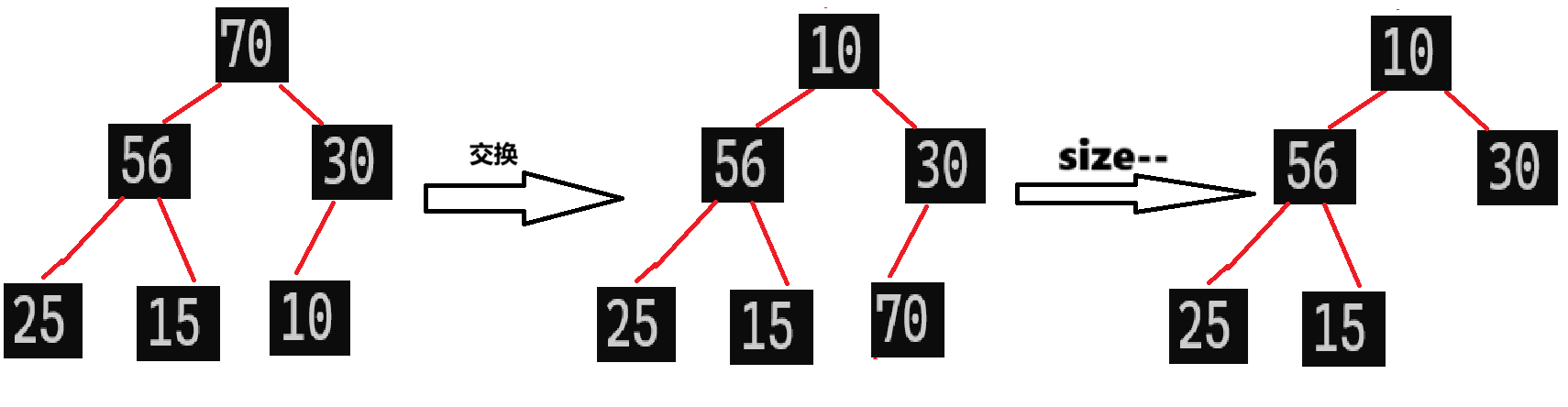
我们知道,在用数组为底的数据结构,我们只用将size--(有效元素个数--)就可以删除尾部元素了,因为在下次遍历的时候是遍历不到这个元素的.所以堆顶与堆底交换之后,再size--,就相当于把堆顶元素删除了,是不是很巧妙?
那么现在有个新的问题,堆底元素上来了,但是不符合大根堆的性质啊,虽然堆的结构没有崩溃,那我们要怎么让10去到正确的位置使得这个堆重新恢复大根堆的性质?这就涉及到我们今天第二个内容---向下调整算法
4.3.3.1、向下调整算法
向下调整算法,顾名思义,就是让元素往下走的算法,在我们交换完堆顶和堆底之后,此时的对顶元素一定小于其子节点
那么这个算法的基本思路就是,将父结点与其子节点比较,如果父结点比子节点小,那就将父节点与子节点交换,以此类推,直到符合大根堆的性质
现在第二个问题来了,每个父结点有两个子节点,应该跟那个比较?跟那个交换?就拿下面这张图为例:
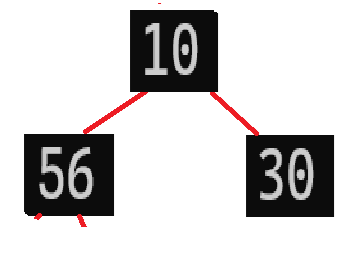
10应该跟56还是30交换?如果跟30交换,那就变成了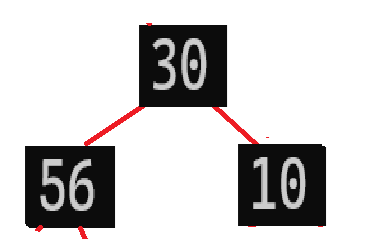
这时候30作为父节点还是比子节点56小,还是要与56交换一遍,所以我们为了效率的提升,直接一步到位:将父结点与其最大的子节点交换,也就是说,10直接和56交换: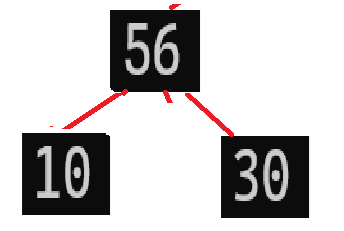
这样直接就满足了父结点比其子节点都要大的性质了,那么,向下调整算法的代码就应该是:
cpp
//现在是向下调整算法(大顶堆):
void adjustDown(Elemtype* arr, int size, int parent) {
assert(arr);
int child = parent * 2 + 1;
while (child < size) {
//这里先比较两个子节点的值,看看哪个更大
//如果是小根堆,那就是比较哪个更小
//所以,在第一个if语句中:
//大根堆:<
//小根堆:>
if (*(arr + child) < *(arr + child + 1)) {
child++;
}
//这里是父节点与子节点进行比较,所以第二个if语句中:
//大根堆:>
//小根堆:<
if(*(arr+parent)>*(arr+child)){
Swap(arr + child, arr + parent);
parent = child;
child = parent * 2 + 1;
}
else {
break;
}
}
}那么,整个出堆的操作的操作代码就应该是:
cpp
//出堆(大顶堆)
void Pop_Heap(Heap* pHeap, int size, int parent) {
//判空
assert(!isEmpty(pHeap));
//将堆顶元素与堆底元素进行交换
Swap(pHeap->arr+parent, pHeap->arr+pHeap->size - 1);
pHeap->size--;
adjustDown(pHeap->arr, pHeap->size, 0);
}哦对了,要注意的是,在出堆中,我们涉及到了交换的操作,我们没有使用库函数,那就自己写一个:
cpp
//现在是交换函数
void Swap(Elemtype* a, Elemtype* b) {
int temp = 0;
temp = *a;
*a = *b;
*b = temp;
}小贴士:在交换代码中,我们传进去的是地址,不是值哦,只有传地址才能修改内容~~~
那么上面就是出堆操作的详解了.
4.3.4、堆的判空
这个操作就很简单了,只用返回结构体中得size值,看看size是不是==0即可:
cpp
//现在是判空代码
bool isEmpty(Heap* pHeap) {
assert(pHeap);
return pHeap->size == 0;
}4.3.5、取最值
这个也简单,就是返回数组的第一个元素:
cpp
//现在是取堆顶
Elemtype Top_Heap(Heap* pHeap) {
return *(pHeap->arr + 0);
}4.3.6、堆的销毁
堆的销毁与顺序表一样,只用将结构体内的元素全部置为0或者NULL即可:
cpp
//现在是堆的销毁
void Destory_Heap(Heap* pHeap) {
pHeap->arr = NULL;
free(pHeap->arr);
pHeap->length = pHeap->size = 0;
}这操作与初始化其实是一样的
那么以上就是堆的基本操作了
五、整体代码:
上面讲完了堆的基本操作,现在是代码的整体实现:
cpp
#define _CRT_SECURE_NO_WARNINGS 520
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<windows.h>
#include<stdbool.h>
//将int重命名
typedef int Elemtype;
//二叉树的顺序存储本质上就是数组,类似线性表,所以结构体与线性表相同
typedef struct Heap {
Elemtype* arr;
int size; //当前二叉树中有效的元素个数
int length; //当前二叉树中的总容量
}Heap; //重命名为heap
//初始化、交换、判空
void Init_Heap(Heap* pHeap);
void Swap(Elemtype* a, Elemtype* b);
bool isEmpty(Heap* pHeap);
//大根堆
void adjustUP(Elemtype* arr, int child);
void adjustDown(Elemtype* arr, int size, int parent);
void Push_Heap(Heap* pHeap, Elemtype data);
void Pop_Heap(Heap* pHeap, int size, int parent);
//小根堆
void adjustUP_small(Elemtype* arr, int child);
void adjustDown_small(Elemtype* arr, int size, int parent);
void Push_Heap_small(Heap* pHeap, Elemtype data);
void Pop_Heap_small(Heap* pHeap, int size, int parent);
//销毁
void Destory_Heap(Heap* pHeap);
//打印
void printf_menu1();
void print_menu2();
void my_printf(Heap* pHeap);
//对堆进行初始化
void Init_Heap(Heap* pHeap) {
pHeap->arr = NULL;
pHeap->size = pHeap->length = 0;
}
//现在是交换函数
void Swap(Elemtype* a, Elemtype* b) {
int temp = 0;
temp = *a;
*a = *b;
*b = temp;
}
//现在是向上调整算法(大顶堆):
void adjustUP(Elemtype* arr, int child) {
int parent = (child - 1) / 2;
while (child > 0) {
if (*(arr+parent) < *(arr+child)) {
Swap(arr+parent, arr+child);
child = parent;
parent = (child - 1) / 2;
}
else {
break;
}
}
}
//现在是向下调整算法(大顶堆):
void adjustDown(Elemtype* arr, int size, int parent) {
assert(arr);
int child = parent * 2 + 1;
while (child < size) {
if (*(arr + child) < *(arr + child + 1)) {
child++;
}
if(*(arr+parent)>*(arr+child)){
Swap(arr + child, arr + parent);
parent = child;
child = parent * 2 + 1;
}
else {
break;
}
}
}
//现在是向上调整算法(小顶堆):
void adjustUP_small(Elemtype* arr, int child) {
int parent = (child - 1) / 2;
while (child > 0) {
if (*(arr + parent) > *(arr + child)) {
Swap(arr + parent, arr + child);
child = parent;
parent = (child - 1) / 2;
}
else {
break;
}
}
}
//现在是向下调整算法(小顶堆):
void adjustDown_small(Elemtype* arr, int size, int parent) {
assert(arr);
int child = parent * 2 + 1;
while (child < size) {
if (child + 1 < size && *(arr + child) > *(arr + child + 1)) {
child++;
}
if(*(arr+parent)>*(arr+child)){
Swap(arr + child, arr + parent);
parent = child;
child = parent * 2 + 1;
}
else {
break;
}
}
}
//堆的插入(大顶堆)
void Push_Heap(Heap* pHeap, Elemtype data) {
//插入是插入在末尾的
//空间不够,增容
if (pHeap->size == pHeap->length) {
//为总容量扩容
int newLength = pHeap->length == 0 ? 4 : 2 * pHeap->length;
//为arr申请一块新的空间
Elemtype* newbase = (Elemtype*)realloc(pHeap->arr, newLength * sizeof(Elemtype));
if (newbase == NULL) {
perror("内存申请失败:");
return;
}
pHeap->arr = newbase;
pHeap->length = newLength;
}
//空间足够:
pHeap->arr[pHeap->size] = data;
//插入之后要用到向上调整算法
adjustUP(pHeap->arr,pHeap->size);
pHeap->size++;
}
//堆的插入(小顶堆)
void Push_Heap_small(Heap* pHeap, Elemtype data) {
//插入是插入在末尾的
//空间不够,增容
if (pHeap->size == pHeap->length) {
//为总容量扩容
int newLength = pHeap->length == 0 ? 4 : 2 * pHeap->length;
//为arr申请一块新的空间
Elemtype* newbase = (Elemtype*)realloc(pHeap->arr, newLength * sizeof(Elemtype));
if (newbase == NULL) {
perror("内存申请失败:");
return;
}
pHeap->arr = newbase;
pHeap->length = newLength;
}
//空间足够:
pHeap->arr[pHeap->size] = data;
//插入之后要用到向上调整算法
adjustUP_small(pHeap->arr, pHeap->size);
pHeap->size++;
}
bool isEmpty(Heap* pHeap) {
assert(pHeap);
return pHeap->size == 0;
}
//出堆(大顶堆)
void Pop_Heap(Heap* pHeap, int size, int parent) {
//判空
assert(!isEmpty(pHeap));
//将堆顶元素与堆底元素进行交换
Swap(pHeap->arr+parent, pHeap->arr+pHeap->size - 1);
pHeap->size--;
adjustDown(pHeap->arr, pHeap->size, 0);
}
//出堆(小顶堆)
void Pop_Heap_small(Heap* pHeap, int size, int parent) {
//判空
assert(!isEmpty(pHeap));
//将堆顶元素与堆底元素进行交换
Swap(pHeap->arr + parent, pHeap->arr + pHeap->size - 1);
pHeap->size--;
adjustDown_small(pHeap->arr, pHeap->size, 0);
}
//现在是堆的销毁
void Destory_Heap(Heap* pHeap) {
pHeap->arr = NULL;
free(pHeap->arr);
pHeap->length = pHeap->size = 0;
}
//现在是取堆顶
Elemtype Top_Heap(Heap* pHeap) {
return *(pHeap->arr + 0);
}
//打印菜单:
void printf_menu1() {
printf("----------------------------------\n");
printf("请先选择你想要的堆顶:\n");
printf("1.大顶堆 2.小顶堆\n");
printf("----------------------------------\n");
}
//打印菜单
void print_menu2() {
printf("==================================\n");
printf("你现在可以进行以下操作:\n");
printf("1.入堆 2.出堆 3.取堆顶元素\n");
printf("==================================\n");
printf("\n");
}
//打印二叉树
void my_printf(Heap* pHeap) {
assert(pHeap);
for (int i = 0; i < pHeap->size; i++) {
printf("%d ", *(pHeap->arr + i));
}
}
//现在是整体代码的实现
int main() {
Heap Hp;
Heap* pHeap = &Hp;
Init_Heap(pHeap);
int choose = 0;
int damndamn = 0;
printf_menu1();
scanf("%d", &damndamn);
switch (damndamn) {
case 1: {
do {
system("cls");
print_menu2();
printf("当前的二叉树为:\n");
my_printf(pHeap);
printf("\n");
printf("请输入你的操作:\n");
scanf("%d", &choose);
switch (choose) {
case 1: {
printf("请输入你想输入的元素个数:\n");
int num = 0;
scanf("%d", &num);
Elemtype data;
printf("请输入你想输入的元素\n");
for (int i = 0; i < num; i++) {
scanf("%d", &data);
Push_Heap(pHeap, data);
}
Sleep(1000);
printf("正在输入...\n");
Sleep(2000);
printf("输入完成!\n");
Sleep(2000);
break;
}
case 2: {
Pop_Heap(pHeap, pHeap->size, 0);
printf("正在出堆\n");
Sleep(2000);
printf("出堆完成...\n");
Sleep(2000);
break;
}
case 3: {
Elemtype top = Top_Heap(pHeap);
printf("堆顶元素为: %d", top);
Sleep(3000);
break;
}
case -1: {
printf("正在退出程序...\n");
Sleep(2000);
printf("退出成功!!!\n");
Sleep(1000);
break;
}
}
} while (choose != -1);
}
case 2: {
do {
system("cls");
print_menu2();
printf("当前的二叉树为:\n");
my_printf(pHeap);
printf("\n");
printf("请输入你的操作:\n");
scanf("%d", &choose);
switch (choose) {
case 1: {
printf("请输入你想输入的元素个数:\n");
int num = 0;
scanf("%d", &num);
Elemtype data;
printf("请输入你想输入的元素\n");
for (int i = 0; i < num; i++) {
scanf("%d", &data);
Push_Heap_small(pHeap, data);
}
Sleep(1000);
printf("正在输入...\n");
Sleep(2000);
printf("输入完成!\n");
Sleep(2000);
break;
}
case 2: {
Pop_Heap_small(pHeap, pHeap->size, 0);
printf("正在出堆\n");
Sleep(2000);
printf("出堆完成...\n");
Sleep(2000);
break;
}
case 3: {
Elemtype top = Top_Heap(pHeap);
printf("堆顶元素为: %d", top);
Sleep(3000);
break;
}
case -1: {
printf("正在退出程序...\n");
Sleep(2000);
printf("退出成功!!!\n");
Sleep(1000);
break;
}
}
} while (choose != -1);
}
}
Destory_Heap(pHeap);
return 0;
}那么以上就是堆的概念、性质以及实现的全部内容分享了,感谢大佬们的阅读~~~
文章是自己写的哈,有什么描述不对的、不恰当的地方,恳请大佬指正,看到后会第一时间修改,感谢您的阅读.