(PS:最近刷了点递归算法题,打算随便写几篇文章小做总结。期末临近,备考ing......)
前言:本文将来简单介绍一下一些使用递归深搜解决二叉树类型的算法题
一,什么是深搜?
初次听说这个概念可能感觉很难理解,其实并非什么高大上的东西。二叉树的深搜可以理解为一个深度优先遍历 。从浅入深的一个遍历过程,拿一个简单的二叉树来举例,深度优先遍历该二叉树的 方式一共有三种,前序遍历,中序遍历以及后序遍历。三种深度优先遍历的区别也只是根节点加入的时机不同。
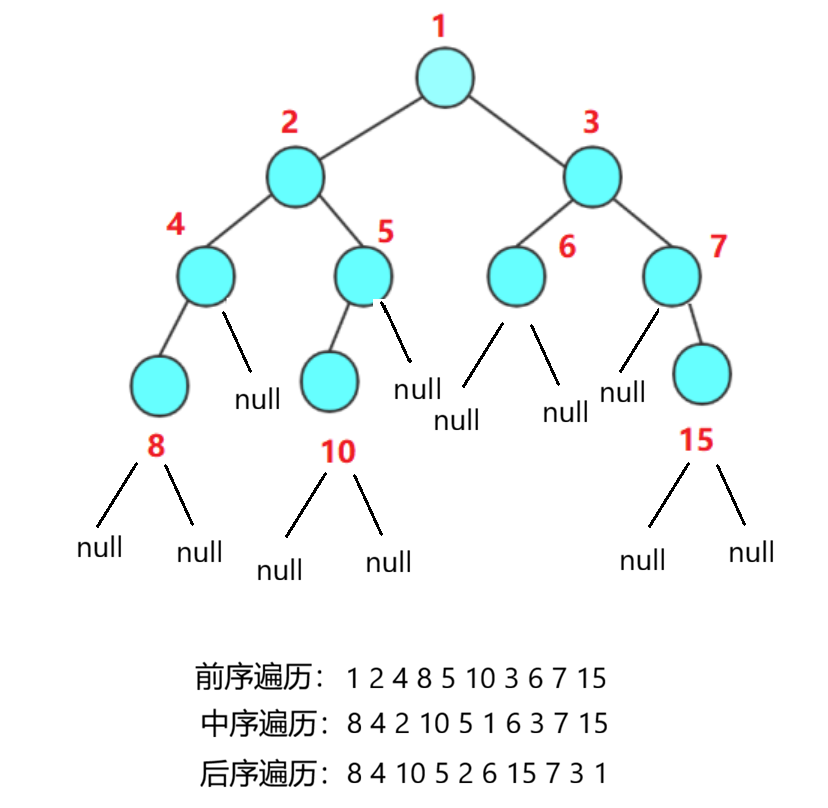
在解决二叉树类型的算法题时,首先要想到使用递归 的方法。因为在遍历二叉树的过程中,每一次遍历都是把子树看做一个独立的树来进行遍历,这种思想与递归思想(解决一个大问题时出现了重复的子问题)不谋而合。举个例子,我们打算前序遍历上图的二叉树,依据根-左-右的顺序添加节点值。首先以1为root节点,先添加根的value ,"1,",然后在遍历左子树,此时root的value为2,这时候就可以把左子树当成一个相同的子类问题进行前序遍历,添加到结果数组中。遍历右子树也是同理。
既然有深搜,那也自然有宽搜,宽搜的特征是逐层遍历,只有遍历完这一层的所有节点之后才能去遍历下一层的节点。
下面来带来几个简单的二叉树算法题。
二,2331. 计算布尔二叉树的值 - 力扣(LeetCode)
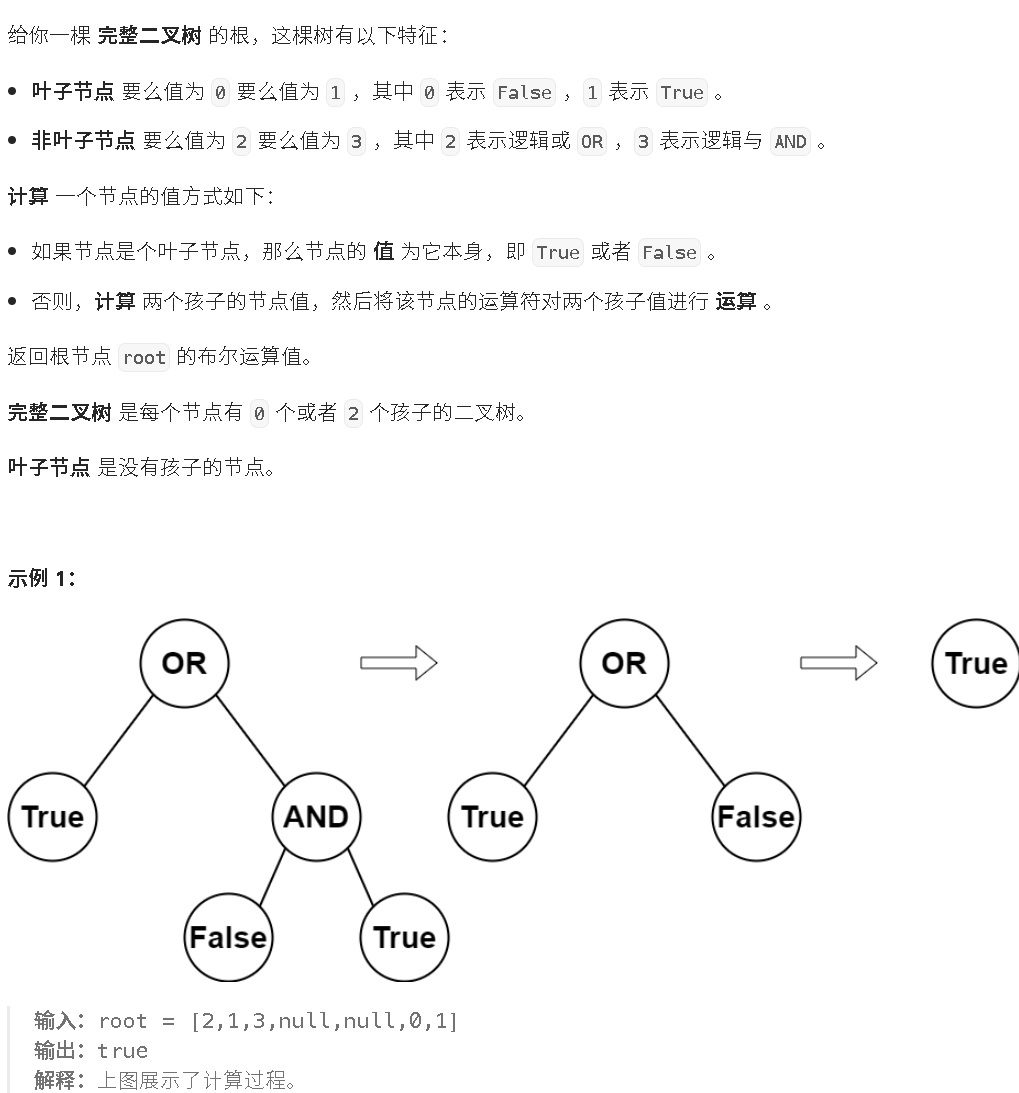
(一)解析
以根节点为基准,如果想要得到整体二叉树的bool值,就需要的得出三个前提条件,分别是根节点的运算符类型,以及左右孩子节点的bool值。试图计算整体二叉树的bool值,就需要计算左右子树的bool值,这就出现了解决一个大问题出现了相同的重复子问题。于是就可以使用递归来解决这个问题。
1.递归函数头如何设计?
函数头的设计需要具体问题具体分析 ,没有固定的模版。比如在使用快速排序时,需要依据基准值划分数组,在对子数组的划分时就需要知道上一层的数组的左右边界and数组元素,于是在设计快排的函数头时就需要把left,right和arr作为参数传给下一层递归才能解决子问题。大体上可以依据这样的一个思路:假如我要解决这个问题,我需要哪些条件(参数),是否需要返回值,哪种类型的返回值?
于是回到现在的问题,假如我们想要得到左子树或者右子树的bool值,上一层递归调用需要给我传入什么参数?按照此方法分析,函数头的参数只需要一个root 来遍历二叉树即可。
2.函数体如何实现任务
在写递归的函数体时,我们要本着一个原则,那就是整体看待问题 ,把递归的解决子问题的过程看做一个黑盒,不必过于关心这个递归内部是如何解决的,递归涉及到递推(dfs)和回归(return),从而减少问题的复杂性。
回到现在的问题,加入我们想要得到root整体子树的bool值,我们需要得到左右子树的bool值,我们可以直接定义两个bool类型的变量,将递归左节点,右节点的值存在变量当中,不必关心这个递归是怎么具体实现的,而是相信这个递归函数一定可以完成任务,把bool值返回给我。最后依据根节点的运算类型return即可
3.递归的结束条件
递归一定要有出口,也就是到什么情况才停止递归。快排递归的出口是子数组内元素个数无法被细分;斐波那契递归的出口是斐波那契数为1或者2时return。遍历题目的二叉树的递归出口就是遍历到叶子节点时不再递归
以上是对于使用递归的注意事项以及简单的总结,后面不再赘述
(二)代码
java
class Solution {
public boolean evaluateTree(TreeNode root) {
return dfs(root);
}
public static boolean dfs(TreeNode root){
if(root.left == null && root.right == null){//遍历到叶子节点停止遍历
return root.val == 1;
}
boolean left = dfs(root.left);//计算左子树bool值
boolean right = dfs(root.right);//计算右子树bool值
return root.val == 2 ? left | right : left & right;
}
}三,129. 求根节点到叶节点数字之和 - 力扣(LeetCode)
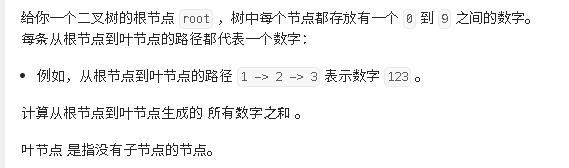
(一)解析
要求是返回从根节点遍历到叶子节点中生成的数字之和,很显然这是一个二叉树的深度优先遍历,这就回到了如何使用递归来解决这个问题
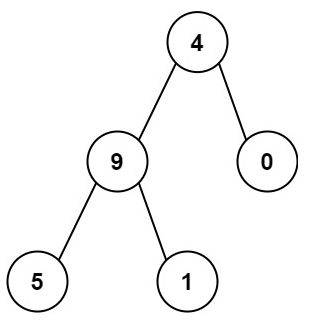
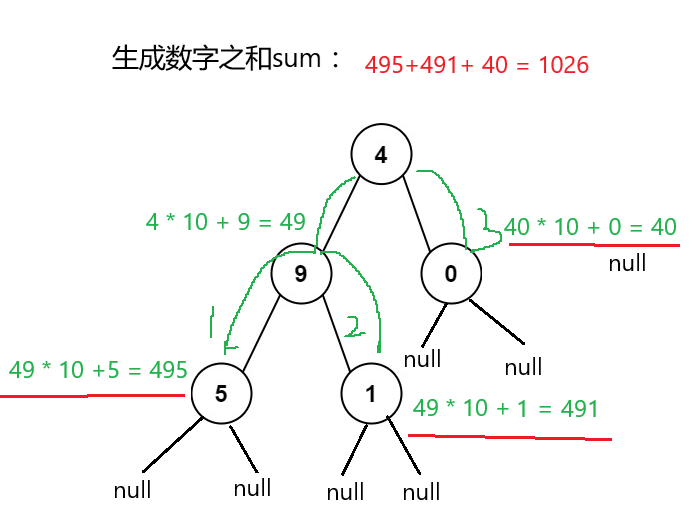
先来简单模拟一下这道题的解题步骤,如下图
1.函数头
函数头的设计在学习递归时需要思考为什么这样设计,如何设计,而不是死记硬背设计的模版、
在设计函数头的时候,我们需要思考:为了解决这样一个子问题,我需要哪些条件?
由每一层二叉树的计算过程可以看到,在计算当前层的数字时,我们需要知道上一层的数字结果,也就是需要把上一层作为我们数字的左边一位参与计算
由此可以得到函数头的设计。
需要遍历整个树 传入根节点
需要上一层的计算结果,传入path
函数头可以设计为 int dfs(root,path)
2.函数体
函数体的设计就是注重于这个子问题是如何实现的,再把这个问题反复调用。可以这么说,递归的函数体就是重复调用一个相同的逻辑去解决一个大问题。关键在于如何找到这个相同的逻辑
观察上面的图片,我们需要计算遍历到当前节点的数字,并把这个数字传递给该节点的孩子节点。
因此,就可得到一个简答的计算步骤。函数头的path代表着我们需要传递给下一层的数字。函数体的维护也就是对于path的计算
path的计算也很简单,path = path * 10 + root.val
随后再依次递归左右子树。无需担心这个递归内部的具体实现,我们只相信这个递归一定可以完成任务,把最终遍历完一次分枝的数字返回给我。直接对sum累加这个返回值即可
3.结束条件
结束条件很简单,也就是递归的出口。没有结束条件递归会一直进行导致死循环。这也是一开始大部分人写递归导致死循环的原因。关于本题,递归的结束条件就是遍历的节点是叶子节点。也就是左右子节点都为null值时结束递归
(二)代码实现
代码如下
java
class Solution {
public int sumNumbers(TreeNode root) {
return dfs(root,0);
}
public int dfs(TreeNode root,int path){
path = path*10 + root.val;
if(root.left == null && root.right == null){//放在path计算逻辑之后,使得只有一个根节点时,根节点值能参与计算
return path;
}
int sum = 0;
if(root.left != null){
sum += dfs(root.left,path);//递归左子树
}
if(root.right != null){
sum += dfs(root.right,path);//递归右子树
}
return sum;
}
}不过一般处理递归我们通常使用一个全局变量的方式,通过全局变量的定义,我们不必关心dfs函数的返回值,只需要让dfs对这个全局变量做出修改即可,参考这种思路,还有下面这种代码
java
class Solution {
private int sum;
public int sumNumbers(TreeNode root) {
sum = 0;
dfs(root,0);
return sum;
}
public void dfs(TreeNode root,int path){
path = path*10 + root.val;
//放在path计算逻辑之后,使得只有一个根节点时,根节点值能参与计算
if(root.left == null && root.right == null){
sum += path;
return;
}
if(root.left != null){
dfs(root.left,path);//递归左子树
}
if(root.right != null){
dfs(root.right,path);//递归右子树
}
}
}(三)细节处理
在递归之前需要加一个if判断条件,避免单分支二叉树的出现导致递归传入的参数root.left 或者root.right是一个null的值
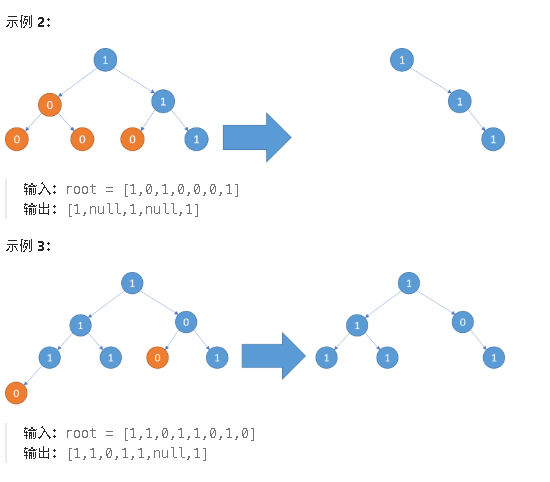
四 ,二叉树剪枝
题目链接 : https://leetcode.cn/problems/binary-tree-pruning/description/
(一)剪枝
这里涉及到了一个新的概念------剪枝
剪枝是什么?从语义上理解好像是把一个二叉树的枝叶给剪去,也就是把不符合条件的节点给去除,没必要遍历这些节点。如果我们自己手动画过递归的展开图,就会知道递归主要包含了两个步骤: 递推and 回归。这种过程会带来大量的冗余计算,使得一个节点被遍历多次。
如果我们使用剪枝的思想,把不符合要求的节点去除,就能减少遍历的次数,提高程序的运行效率。
如何实现剪枝?其实也就是dfs函数体内部加一个if判断语句,依据if语句的结果来决定是继续向下递推还是直接返回return。有关如何使用剪枝,在这道题中也会体现出来
(二)解析
分析题意,我们需要把所有不包含1的二叉树的子树都给减掉。大白话就是一个子树中,只要都是由0构成的的,那就把这个子树给给删除。然后将剩余的子树返回
1.函数头
深度优先遍历,需要传入root。接下来是返回值设计。是void还是传入一个TreeNode类型的?
在思考这个类型前得弄清出dfs的功能。假定我们设计的dfs函数的作用是:我给你一个根节点root,你把你左子树中只包含0的子树删除;把右子树中只包含0的子树删除,把修改后的二叉树给我即可。这样一来返回值的类型很明显就是TreeNode类型。
2.函数体
把你左子树中只包含0的子树删除;把右子树中只包含0的子树删除,这个过程需要用到深度优先遍历,因为需要从叶子节点开始删除操作。这里也就有一个问题,深度优先遍历的如何选择?是使用前序,中序,还是后序遍历?结合题目来分析:
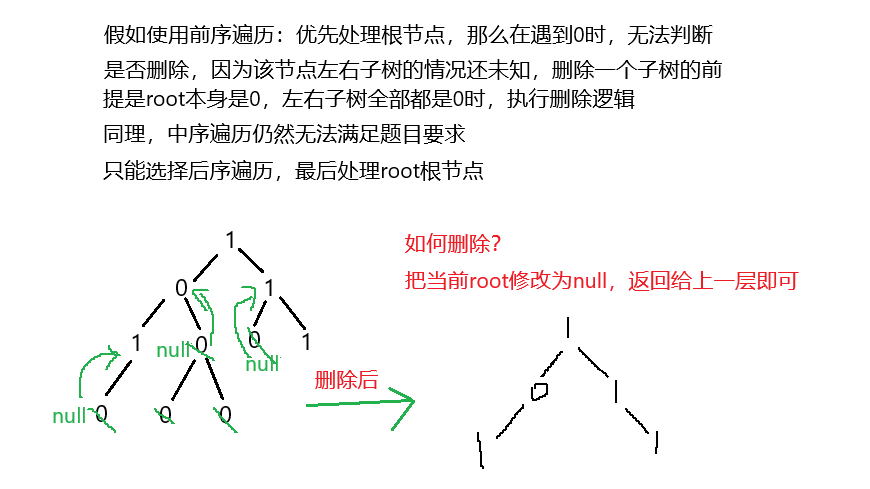
3.结束条件、
在遍历到叶子节点时即可结束递归,由于叶子节点为null,直接返回给上一层即可
(三)代码实现
java
class Solution {
public TreeNode pruneTree(TreeNode root) {
return dfs(root);
}
public TreeNode dfs(TreeNode root){
if(root == null){
return root;
}
//后序遍历
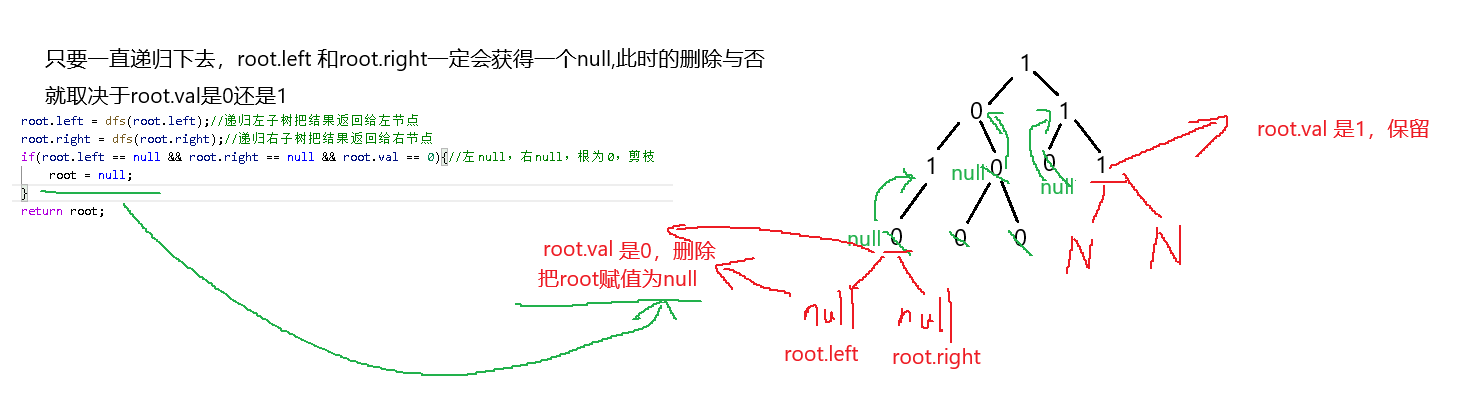
root.left = dfs(root.left);//递归左子树把结果返回给左节点
root.right = dfs(root.right);//递归右子树把结果返回给右节点
if(root.left == null && root.right == null && root.val == 0){//左null,右null,根为0,剪枝
root = null;
}
return root;
}
}(四)细节处理
(五)98. 验证二叉搜索树
题目链接:https://leetcode.cn/problems/validate-binary-search-tree/description/
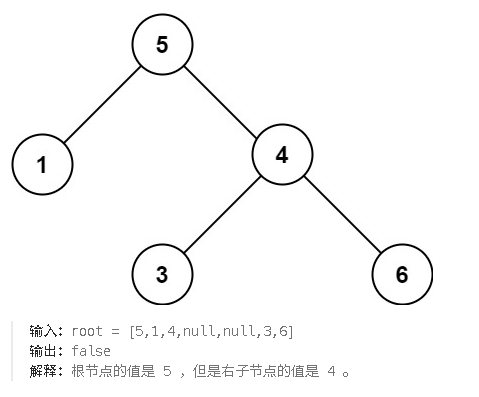
(一)解析
题目要求我们去验证一个二叉树是否是二叉搜索树。二叉搜索树的概念是根节点的值大于左节点,根节点的值小于右节点。对二叉搜索树进行中序遍历是一个升序的序列。这是核心特征,于是我们在解决这道题时就可以使用中序遍历二叉树
结合题目,需要判断二叉树是否满足二叉搜索树,使用中序遍历的思想来看一种解法是在遍历的过程中维护一个prev值 ,我一般叫前驱值。假如这棵树是二叉搜索树,那么在中序遍历是,rooot.val一定会大于 prev的值。反之就不是。一般的思想是维护一个数组,但是空间消耗太大而且还得判断数组是否是升序排列的,所以单单维护一个prev变量比较方便。在递归的问题中,每一个递归都需要访问的数据设为全局变量的方式比较方便使用。
下面来简单模拟一下流程
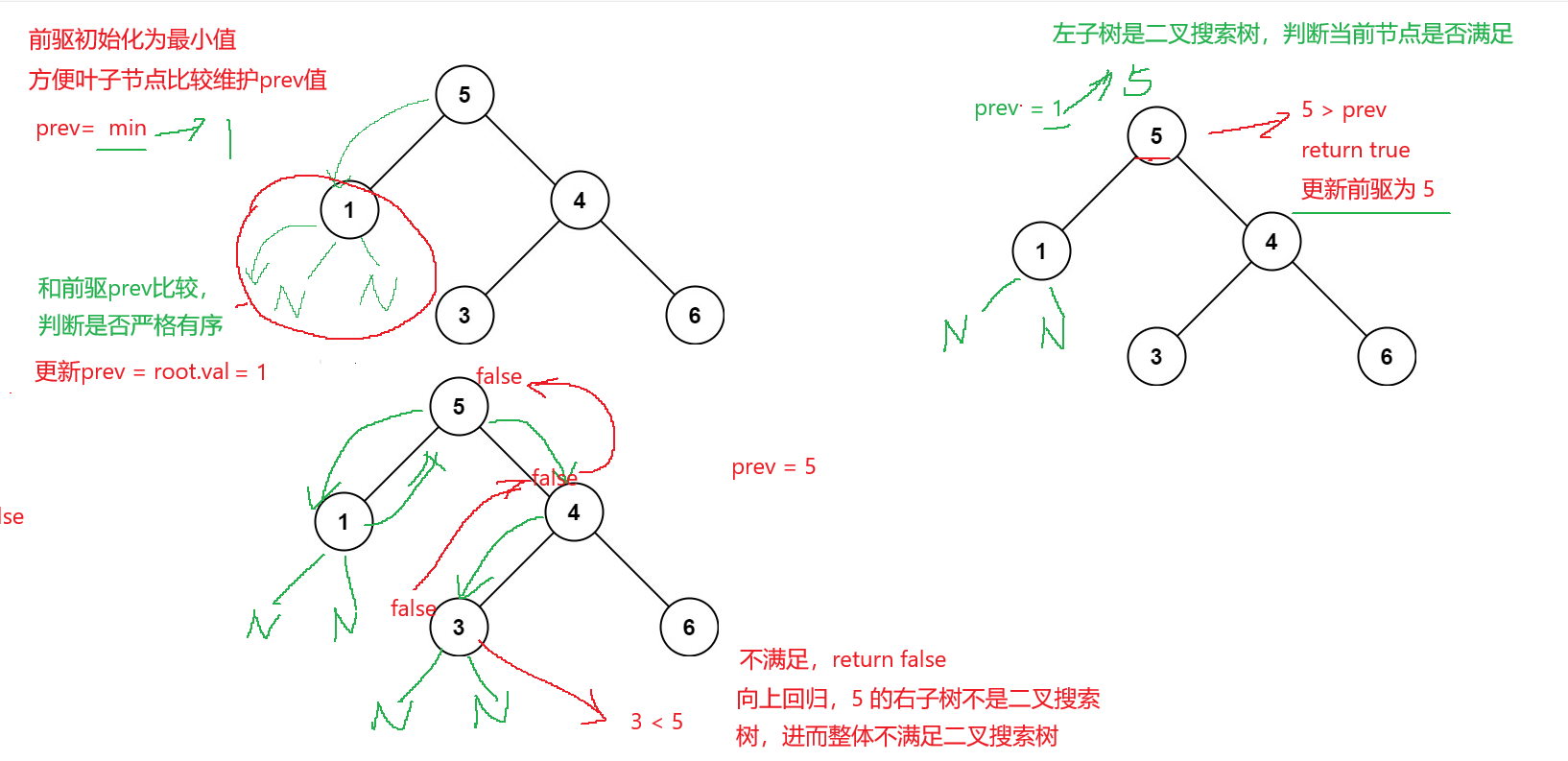
于是这里我们dfs函数的任务就是判断一个二叉树是否是二叉搜索树
(二)函数头
深度遍历传入 root ,题目给定的原函数可以作为dfs函数
(三)函数体
先对所给参数判空,root 为null 时也是一个二叉搜索树。
然后按照中序遍历的思路,对当前节点的左子树遍历,得到一个bool类型的返回值,此时可以采用剪枝,若左子树返回值为false,则没必要再遍历直接return false。之后对当前节点值和前驱值prev比较,判断中序遍历的结果是否有序,这里同样可以插入剪枝。右子树遍历同理
(四)代码实现
java
class Solution {
private long prev = Long.MIN_VALUE;
public boolean isValidBST(TreeNode root) {
if(root == null) return true;
boolean left = isValidBST(root.left);
if(left == false) return false;//剪枝
boolean cur = false;//当前节点是否是二叉搜索树
if(root.val > prev) {
cur = true;//当前节点值大于前驱,符合
}else return false;//当前节点值小于前驱,剪枝
prev = root.val;//更新前驱prev值
boolean right = isValidBST(root.right);
return cur && left && right;//根,左,右都为二叉搜索树才return true
}
}二叉树深搜从代码上来看很简洁,但是需要考虑的细节却很ex,一不小就会出现死循环,空指针异常。所以在解决这类问题时还是得先弄清楚dfs函数具体任务,也就是我要给这个dfs函数下达什么任务,它能为我完成什么事。听着有点抽象,三言两语很难阐述明白,所以还是得多画图,多做题。
后序也会分享一些关于递归的算法题。
(PS :期末备考,得着手复习了,希望能过)