SLAM文献之-Embedding Manifold Structures into Kalman Filters（2)

V. 流形上的误差状态卡尔曼滤波器

在本章中，我们基于典型系统表示式 (16) 推导符号化卡尔曼滤波器。为了避免系统原始状态在流形上的最小参数化奇异性，我们采用了误差状态（error-state）思想，这在之前的工作如 [6] 和 [16] 中已有研究。所呈现的推导非常抽象，但更加简洁、紧凑且通用。此外，为了完整说明，我们还推导了全多速率迭代卡尔曼滤波器。读者可参考 [6] 获取更详细的推导/解释，或参考 [16] 了解具体示例的简要推导。

在下面的叙述中，我们使用以下符号约定：

S S S 表示状态 x x x 所在的流形， M M M 表示测量 z z z 所在的流形。为了简化符号，当上下文清楚时，操作符 ⊞ \boxplus ⊞ 和 ⊟ \boxminus ⊟ 可省略下标 S , M S, M S,M。
下标 k k k 表示时间索引，例如 x k x_k xk 是第 k k k 步的状态 x x x 的真实值。
下标 τ ∣ k \tau|k τ∣k 表示基于到第 k k k 步的所有测量对某量在第 τ \tau τ 步的估计，例如 x τ ∣ k x_{\tau|k} xτ∣k 表示基于到第 k k k 步测量对状态 x τ x_\tau xτ 的估计。对于滤波问题，需 τ ≥ k \tau \ge k τ≥k。更具体地： τ > k \tau > k τ>k 表示状态预测（先验估计）， τ = k \tau = k τ=k 表示状态更新（后验估计）。
δ x τ ∣ k = x τ ⊟ x τ ∣ k \delta x_{\tau|k} = x_\tau \boxminus x_{\tau|k} δxτ∣k=xτ⊟xτ∣k 表示在 x τ ∣ k x_{\tau|k} xτ∣k 的切空间中的估计误差。由于真实状态 x x x 是随机的，因此 δ x τ ∣ k ∈ R n \delta x_{\tau|k} \in \mathbb{R}^n δxτ∣k∈Rn。
P τ ∣ k P_{\tau|k} Pτ∣k 表示估计误差 δ x τ ∣ k \delta x_{\tau|k} δxτ∣k 的协方差矩阵。
上标 j j j 表示迭代卡尔曼滤波器的第 j j j 次迭代，例如 x k ∣ k j x^j_{k|k} xk∣kj 表示基于到第 k k k 步测量的状态 x k x_k xk 在第 j j j 次迭代的估计。

A. 初始化

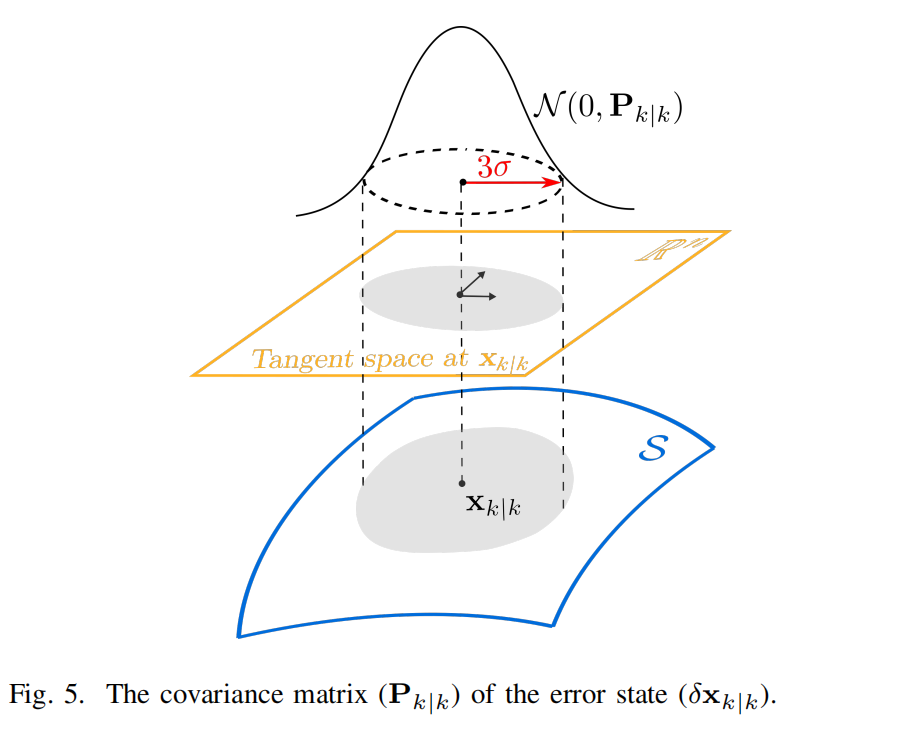
假设我们已收到到第 k k k 步的测量，并将该时刻的状态更新为 x k ∣ k x_{k|k} xk∣k，同时更新协方差矩阵为 P k ∣ k P_{k|k} Pk∣k。根据上述符号约定， P k ∣ k P_{k|k} Pk∣k 表示 δ x k ∣ k \delta x_{k|k} δxk∣k（状态更新 x k ∣ k x_{k|k} xk∣k 的切空间误差）的协方差矩阵。 δ x k ∣ k \delta x_{k|k} δxk∣k 与 P k ∣ k P_{k|k} Pk∣k 的关系如图 5 所示。

B. 状态传播

从第 k k k 步开始的状态传播可直接由系统模型 (16) 推导，设 w = 0 w = 0 w=0：

x k + 1 = x k ⊕ ( Δ t f ( x k , u k , 0 ) ) (24) x_{k+1} = x_k \oplus (\Delta t f(x_k, u_k, 0)) \tag{24} xk+1=xk⊕(Δtf(xk,uk,0))(24)

如果只需要传播一步，这通常发生在测量的采样率与输入相同的情况下，则 τ = k \tau = k τ=k。否则，状态传播会在每次输入时进行，并在接收到测量时停止。

C. 误差状态系统

误差状态卡尔曼滤波器在误差状态空间中传播协方差矩阵，以避免在 x x x 中的过度参数化。对于 τ ≥ k \tau \ge k τ≥k，误差状态定义为：

δ x τ ∣ k = x τ ⊟ x τ ∣ k , τ ≥ k . (25) \delta x_{\tau|k} = x_\tau \boxminus x_{\tau|k}, \quad \tau \ge k. \tag{25} δxτ∣k=xτ⊟xτ∣k,τ≥k.(25)

将式 (16) 和 (24) 代入 (25) 可得：

δ x τ + 1 ∣ k = x τ + 1 ⊟ x τ + 1 ∣ k = ( x τ ⊕ ( Δ t f ( x τ , u τ , w τ ) ) ) ⊟ ( x τ ∣ k ⊕ ( Δ t f ( x τ ∣ k , u τ , 0 ) ) ) (26) \delta x_{\tau+1|k} = x_{\tau+1} \boxminus x_{\tau+1|k} = \big(x_\tau \oplus (\Delta t f(x_\tau, u_\tau, w_\tau))\big)\\ \boxminus (x_{\tau|k}\oplus(\Delta t f({x_{\tau|k}}, u_\tau, 0)))\tag{26} δxτ+1∣k=xτ+1⊟xτ+1∣k=(xτ⊕(Δtf(xτ,uτ,wτ)))⊟(xτ∣k⊕(Δtf(xτ∣k,uτ,0)))(26)

将式 (25) 代入上式可得：

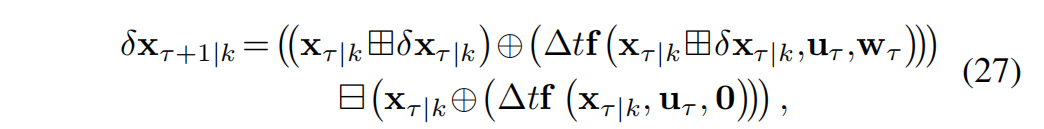
该系统从 τ = k \tau = k τ=k 开始定义一个新的系统。该系统描述了误差状态 δ x τ ∣ k \delta x_{\tau|k} δxτ∣k 的时间演化，因此被称为误差状态系统。由于新的误差状态系统源自当前测量时刻 k k k ，每当收到新测量以更新状态估计时，它会被重新定义。这样的重复过程有效地将误差轨迹限制在单位元的邻域内，从而验证了 δ x τ ∣ k \delta x_{\tau|k} δxτ∣k 的最小参数化。

在 S S S 为李群（Lie group）的情况下，状态 x τ ∣ k x_{\tau|k} xτ∣k 切空间中的误差状态为：

δ x τ ∣ k = log ⁡ ( x τ ∣ k − 1 ⋅ x τ ) \delta x_{\tau|k} = \log \big( x_{\tau|k}^{-1} \cdot x_\tau \big) δxτ∣k=log(xτ∣k−1⋅xτ)

定义在原流形 S S S 上的误差状态为 x τ ∣ k e = x τ − 1 ⋅ x τ x^e_{\tau|k} = x_\tau^{-1} \cdot x_\tau xτ∣ke=xτ−1⋅xτ ，两个轨迹 δ x τ ∣ k \delta x_{\tau|k} δxτ∣k 与 x τ ∣ k e x^e_{\tau|k} xτ∣ke 之间的关系如图 1 所示。

由于误差系统 (27) 具有最小参数化，因此可以采用标准的卡尔曼滤波器变体（Kalman filter variants）。相应地，两个卡尔曼滤波步骤------传播（propagation）和更新（update）------分别称为"误差状态传播（error-state propagation）"和"误差状态更新（error-state update）"，以便与原状态空间 (16) 区分开来。在接下来的内容中，我们将详细展示误差状态的传播与更新过程。

1.初始条件 ：误差系统 (27) 从 τ = k \tau = k τ=k 开始。初始估计为

δ x k ∣ k ∣ k = ( x k ⊟ x k ∣ k ) ∣ k = x k ∣ k ⊟ x k ∣ k = 0 (28) \delta x_{k|k|k} = (x_k \boxminus x_{k|k}){|k} =x{k|k} \boxminus x_{k|k}= 0\tag{28} δxk∣k∣k=(xk⊟xk∣k)∣k=xk∣k⊟xk∣k=0(28)

这里，记号 δ x ( k ∣ k ) ∣ k \delta x(k|k)|_k δx(k∣k)∣k 表示基于截止到时刻 k k k 的测量对随机向量 δ x k ∣ k \delta x_{k|k} δxk∣k 的估计（回顾一下，由于其在公式 (25) 中的定义，以及真实状态 x k x_k xk 本身也是随机的，所以 δ x k ∣ k \delta x_{k|k} δxk∣k 确实是随机的）。公式 (28) 的结果并不令人意外，因为 δ x k ∣ k \delta x_{k|k} δxk∣k 已经是在条件于截止到时刻 k k k 的测量后的误差，因此再次条件于相同的测量不会提供更多信息。

误差状态传播 ：误差状态的传播直接来自误差状态系统模型 (27)，通过令 w = 0 w = 0 w=0 得到：

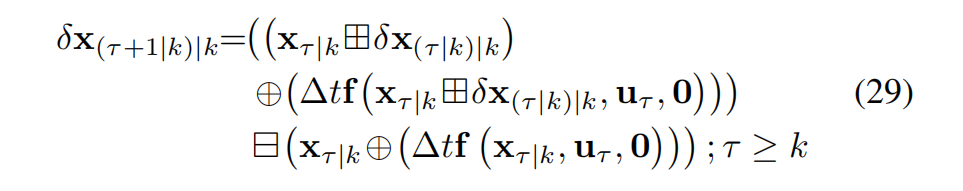
从初始条件 (28) 出发，我们得到：

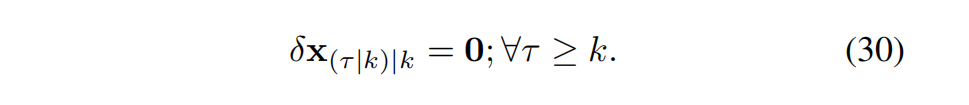
接下来，为了传播误差协方差，我们需要对系统 (27) 进行线性化，如下所示：

δ x τ + 1 ∣ k ≈ F x τ δ x τ ∣ k + F w τ w τ (31) \delta x_{\tau+1|k} \approx F_{x_\tau} \delta x_{\tau|k} + F_{w_\tau} w_\tau \tag{31} δxτ+1∣k≈Fxτδxτ∣k+Fwτwτ(31)

其中， F x τ F_{x_\tau} Fxτ 是在点 δ x ( τ ∣ k ) ∣ k = 0 \delta x(\tau|k)|k = 0 δx(τ∣k)∣k=0 处对 (27) 关于 δ x τ ∣ k \delta x_{\tau|k} δxτ∣k 的偏导数，具体为：

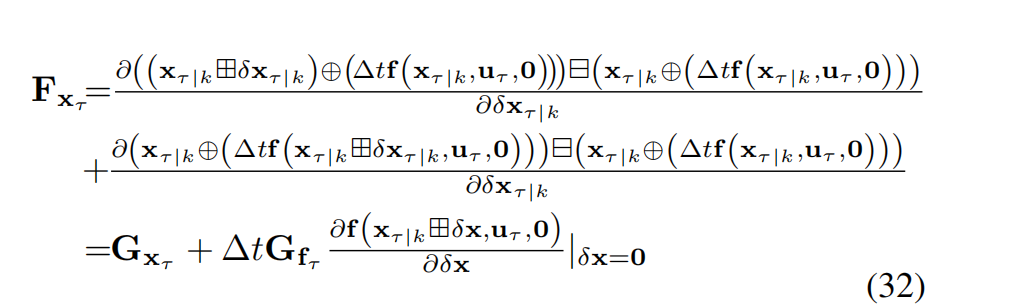
而 F w τ F_{w_\tau} Fwτ 是在点 w τ = 0 w_\tau = 0 wτ=0 处对 (27) 关于 w τ w_\tau wτ 的偏导数，具体为：

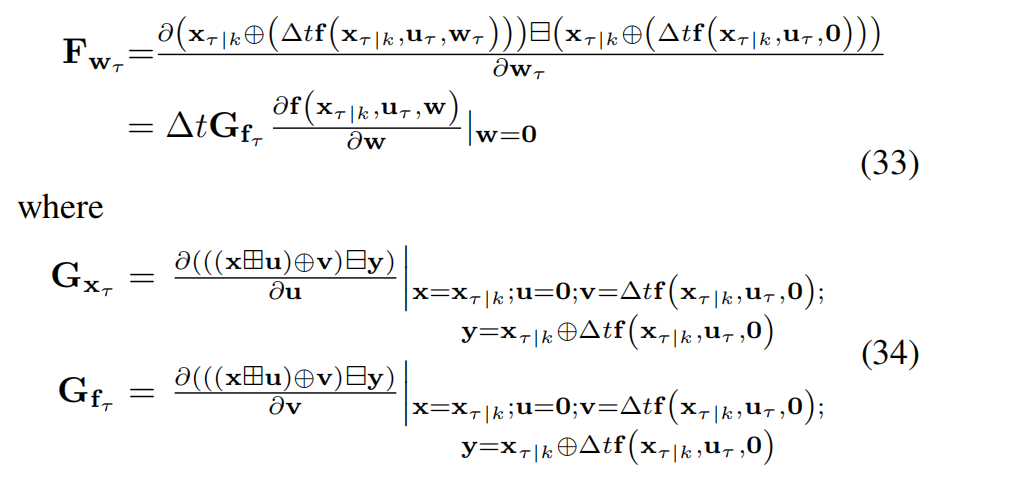
最后，协方差传播为：

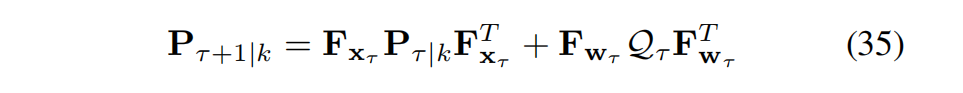
式 (24) 中的状态传播及其对应的协方差传播（式 (35)）如图 6 所示。

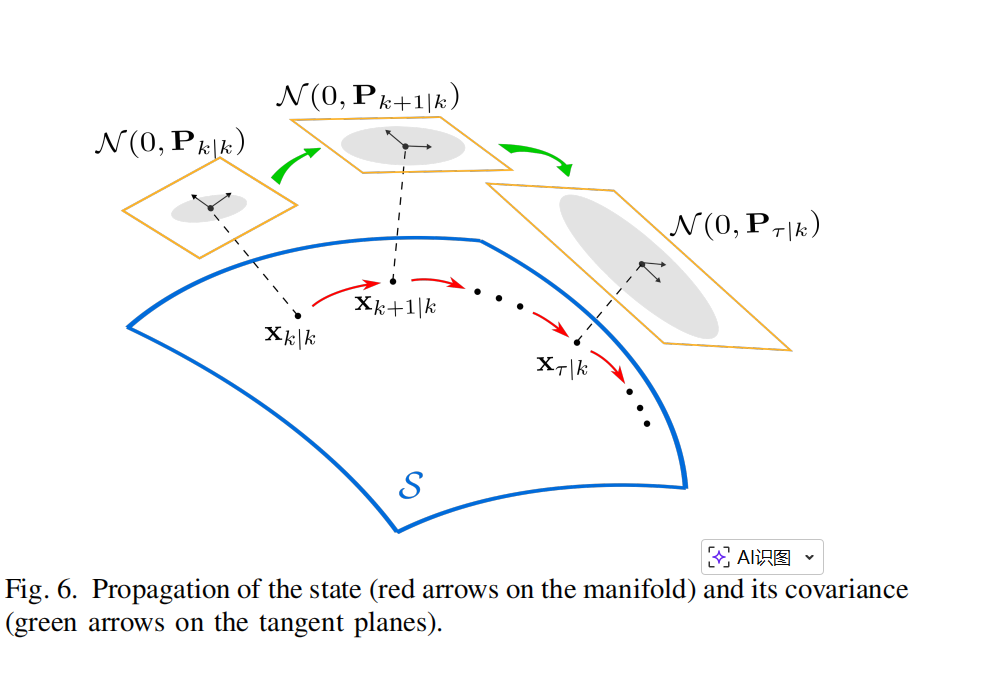
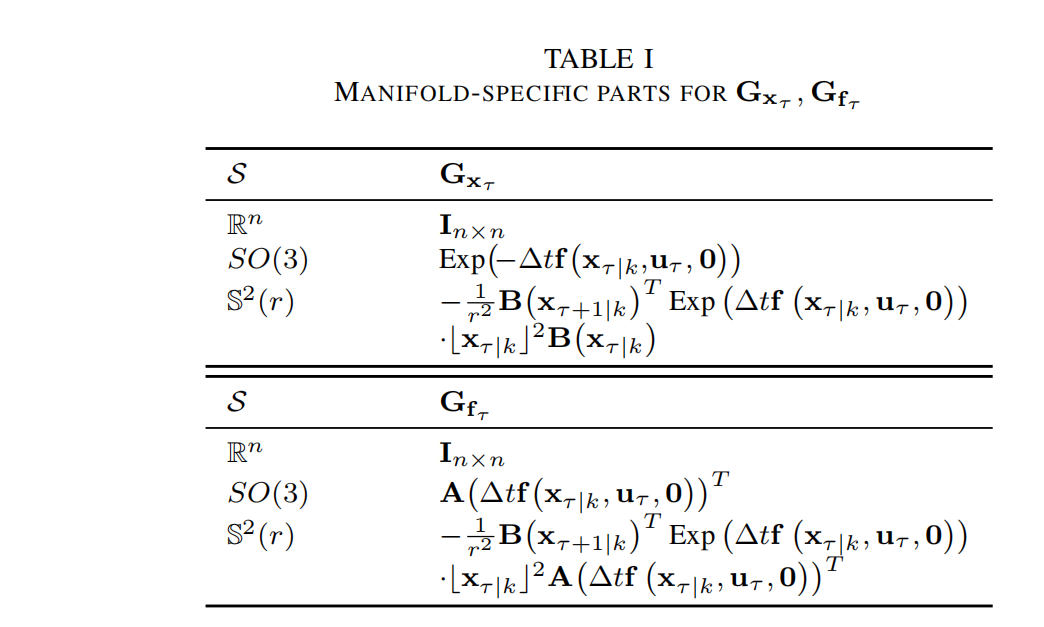
3. 流形结构的分离 ：如式 (32) 和 (33) 所示，两个系统矩阵 F x τ F_{x_\tau} Fxτ 和 F w τ F_{w_\tau} Fwτ 已经很好地分离为流形特定部分 G x τ G_{x_\tau} Gxτ、 G f τ G_{f_\tau} Gfτ 与系统特定部分

∂ f ( x τ ∣ k ⊞ δ x , u τ , 0 ) ∂ δ x ∣ δ x = 0 , ∂ f ( x τ ∣ k , u τ , w ) ∂ w ∣ w = 0 . \frac{\partial f(x_{\tau|k} \boxplus \delta x, u_\tau, 0)}{\partial \delta x} \Big|{\delta x=0}, \quad \frac{\partial f(x_{\tau|k}, u_\tau, w)}{\partial w} \Big|_{w=0}. ∂δx∂f(xτ∣k⊞δx,uτ,0) δx=0,∂w∂f(xτ∣k,uτ,w) w=0.

常用流形的流形特定部分列于表 I。此外，根据式 (15)，任意复合流形的流形特定部分可通过这些原始流形的对应部分进行拼接得到。

D. 状态更新

1. 先验分布 ：假设在步骤 τ > k \tau > k τ>k 时接收到测量。为不失一般性，我们令 τ = k + 1 \tau = k+1 τ=k+1，即测量率等于输入率。传播得到的误差状态 δ x k + 1 ∣ k \delta x_{k+1|k} δxk+1∣k 及其协方差 P k + 1 ∣ k P_{k+1|k} Pk+1∣k 形成 x k + 1 x_{k+1} xk+1 的先验分布：

δ x k + 1 ∣ k = x k + 1 ⊟ x k + 1 ∣ k ∼ N ( 0 , P k + 1 ∣ k ) , (36) \delta x_{k+1|k} = x_{k+1} \boxminus x_{k+1|k} \sim N(\mathbf{0}, P_{k+1|k}),\tag{36} δxk+1∣k=xk+1⊟xk+1∣k∼N(0,Pk+1∣k),(36)

2. 迭代更新 ：现在假设在 k + 1 k+1 k+1 时接收到新测量 z k + 1 z_{k+1} zk+1。在第 j j j 次迭代中，状态估计为 x k + 1 ∣ k + 1 j x^j_{k+1|k+1} xk+1∣k+1j，其中对于 j = 0 j=0 j=0，有

X k + 1 ∣ k + 1 j = x k + 1 ∣ k X^j_{k+1|k+1} = x_{k+1|k} Xk+1∣k+1j=xk+1∣k

即使用先验估计。然后定义残差为：

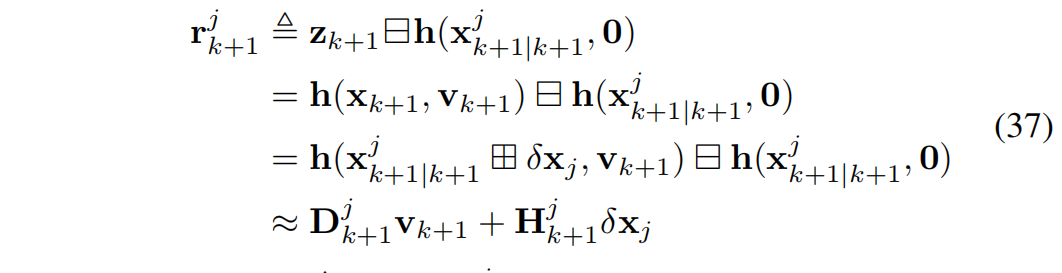
其中 δ x j ≜ x k + 1 ⊟ X k + 1 ∣ k + 1 j \delta x_j \triangleq x_{k+1} \boxminus X^j_{k+1|k+1} δxj≜xk+1⊟Xk+1∣k+1j 表示真实状态 x k + 1 x_{k+1} xk+1 与其最近估计 x k + 1 ∣ k + 1 j x^j_{k+1|k+1} xk+1∣k+1j 之间的误差，并且

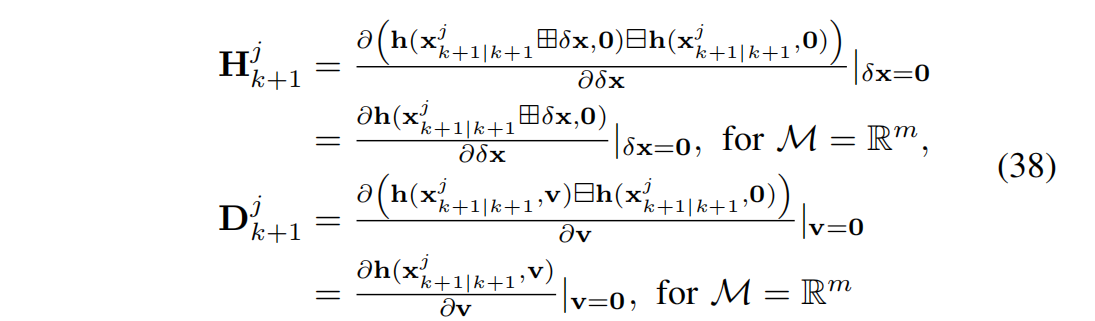
方程 (37) 定义了 δ x j \delta x^j δxj 的后验分布（a posteriori distribution）。

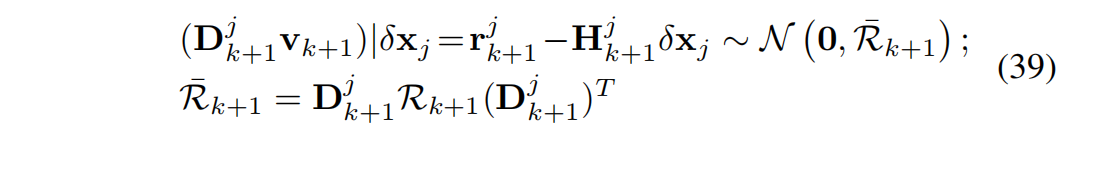
另一方面，方程 (36) 定义了先验估计误差的分布：

δ x k + 1 ∣ k ∼ N ( 0 , P k + 1 ∣ k ) \delta x_{k+1|k} \sim N(0, P_{k+1|k}) δxk+1∣k∼N(0,Pk+1∣k)

它位于 x k + 1 ∣ k x_{k+1|k} xk+1∣k 的切空间中。如图 7 所示，将 δ x k + 1 ∣ k \delta x_{k+1|k} δxk+1∣k 投影到 x k + 1 ∣ k + 1 j x^j_{k+1|k+1} xk+1∣k+1j 的切空间得到：

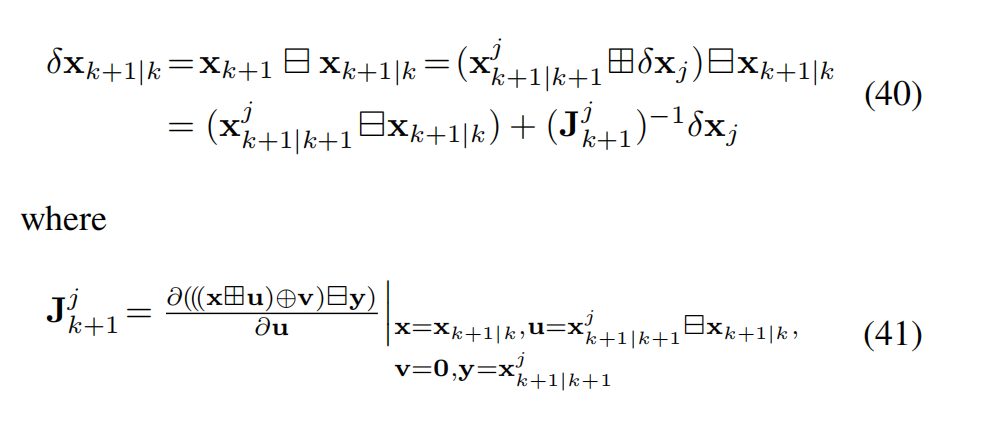
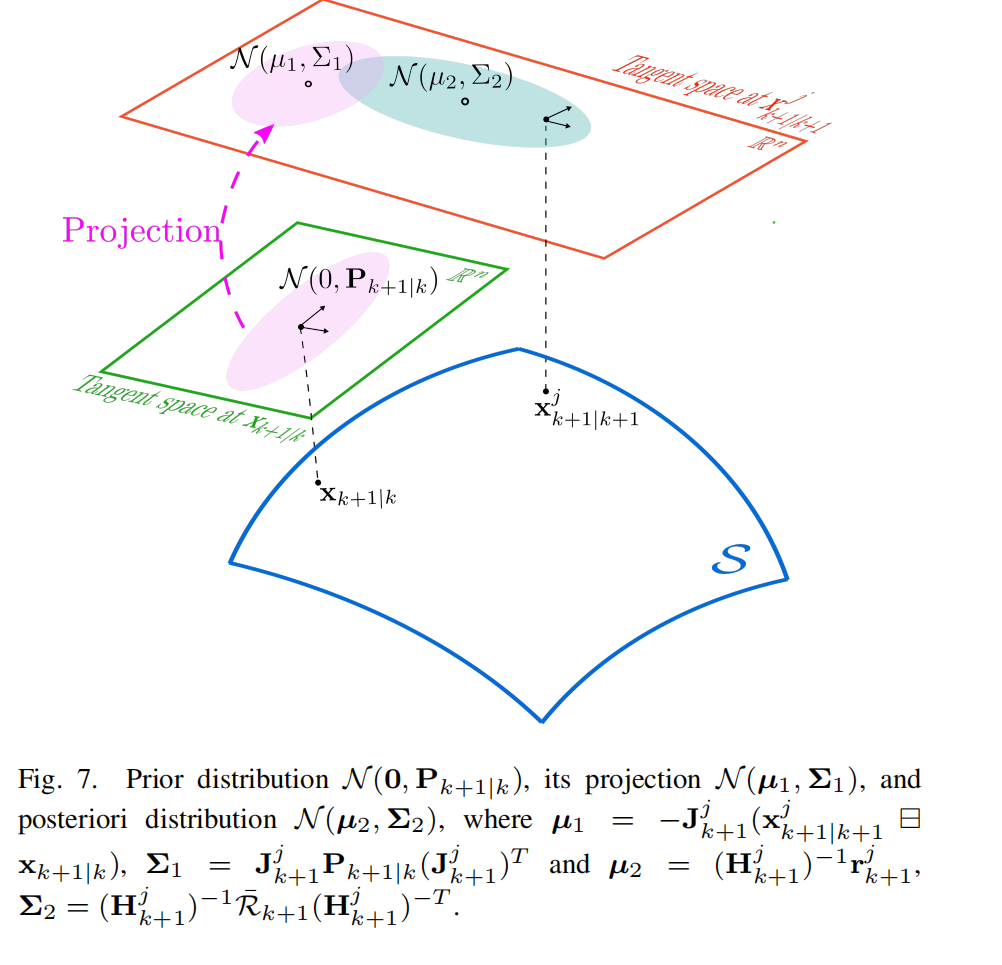
是 δ x k + 1 ∣ k \delta x_{k+1|k} δxk+1∣k 对 δ x j \delta x_j δxj 在零点处的雅可比逆矩阵。然后， δ x j \delta x_j δxj 的等效先验分布为：

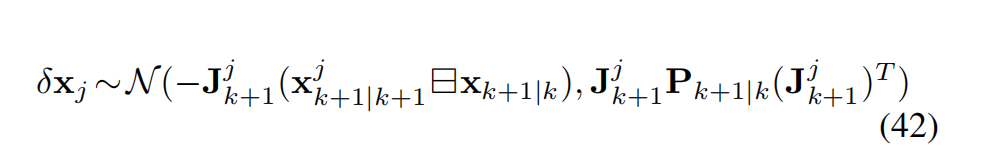
将先验分布 (42) 与后验分布 (39) 结合，可得到 δ x j \delta x_j δxj 的最大后验估计 (MAP)（参见图 7）：

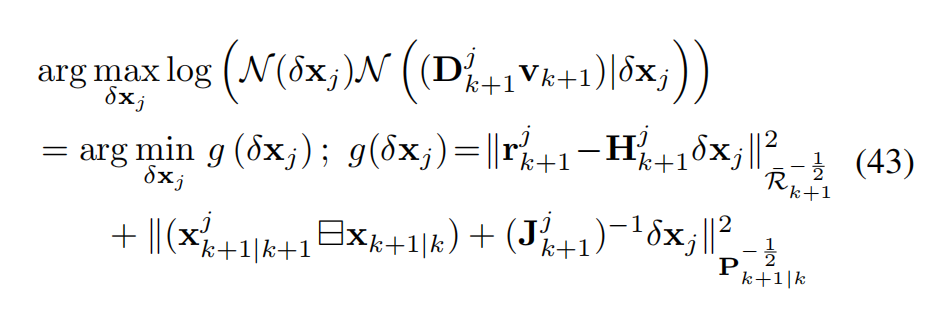
其中 ∣ ∣ x ∣ ∣ A 2 = ∣ ∣ A x ∣ ∣ 2 = x T A T A x ||x||_A^2 = ||Ax||^2 = x^T A^T A x ∣∣x∣∣A2=∣∣Ax∣∣2=xTATAx。式 (43) 的最优解 δ x o \delta x_o δxo 导致如下的卡尔曼更新（Kalman update） [35]：

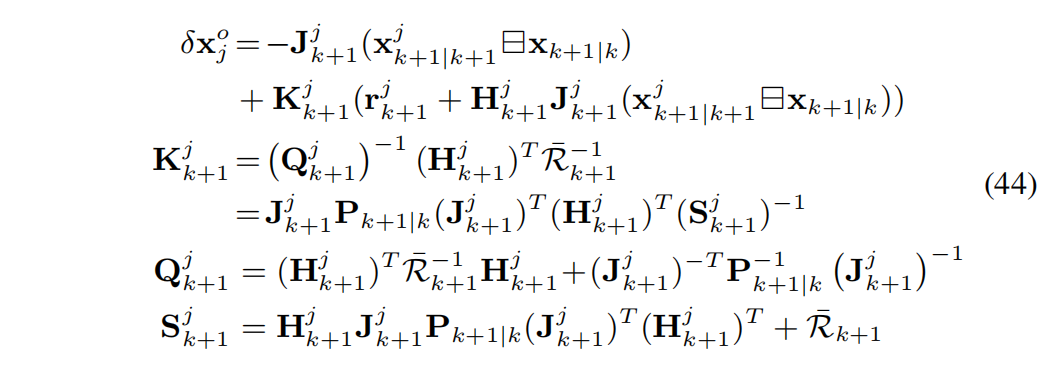
其中 Q k + 1 j Q^j_{k+1} Qk+1j 是公式 (43) 的 Hessian 矩阵，其逆矩阵表示 δ x j − δ x j o \delta x_j - \delta x^o_j δxj−δxjo 的协方差矩阵，进一步可以写成如下形式 [35]：

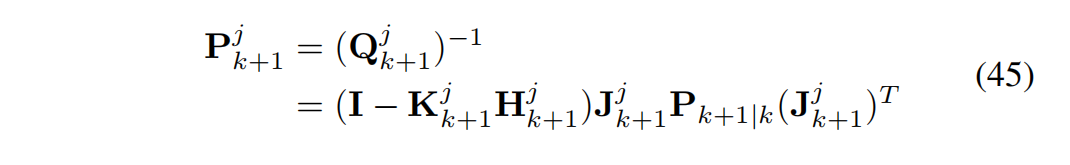
利用最优 δ x j o \delta x^o_j δxjo， x k + 1 x_{k+1} xk+1 的估计更新为

x k + 1 ∣ k + 1 j + 1 = x k + 1 ∣ k + 1 j ⊞ δ x j o (46) x^{j+1}{k+1|k+1} = x^{j}{k+1|k+1} \boxplus \delta x^o_j \tag{46} xk+1∣k+1j+1=xk+1∣k+1j⊞δxjo(46)

上述过程会迭代，直到收敛或达到最大迭代步数。

3. 协方差重置 ：

假设迭代更新在经过 κ ≥ 0 \kappa \ge 0 κ≥0 次迭代后停止，得到 MAP 估计 x k + 1 ∣ k + 1 κ x^{\kappa}{k+1|k+1} xk+1∣k+1κ 及协方差矩阵 P k + 1 κ P^{\kappa}{k+1} Pk+1κ。那么 x k + 1 ∣ k + 1 κ x^{\kappa}{k+1|k+1} xk+1∣k+1κ 成为 x k + 1 x{k+1} xk+1 的 Kalman 更新：

x k + 1 ∣ k + 1 = x k + 1 ∣ k + 1 κ (47) x_{k+1|k+1} = x^{\kappa}_{k+1|k+1} \tag{47} xk+1∣k+1=xk+1∣k+1κ(47)

并传递到 Kalman 滤波器的下一步。对于 P k + 1 κ P^{\kappa}{k+1} Pk+1κ，注意它描述的是 δ x κ − δ x κ o \delta x^{\kappa} - \delta x^o{\kappa} δxκ−δxκo 的协方差，该协方差位于 x k + 1 ∣ k + 1 κ x^{\kappa}{k+1|k+1} xk+1∣k+1κ 的切空间中，而下一步 Kalman 滤波器需要的是描述 δ x k + 1 ∣ k + 1 \delta x{k+1|k+1} δxk+1∣k+1 的协方差 P k + 1 ∣ k + 1 P_{k+1|k+1} Pk+1∣k+1，其位于 x k + 1 ∣ k + 1 x_{k+1|k+1} xk+1∣k+1 的切空间中（见 V-A 节）。这种差异需要一个投影步骤，如图 8 所示。根据误差状态在 (25) 的定义，我们有：

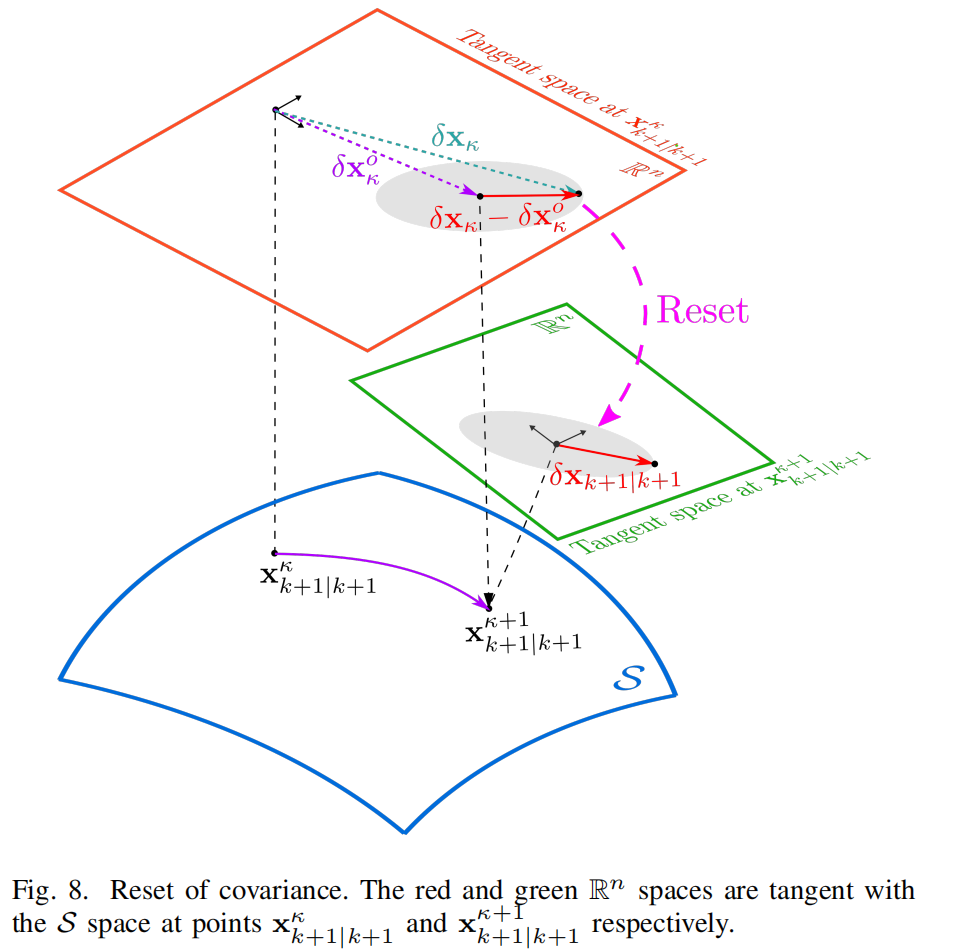
δ x k + 1 ∣ k + 1 = x k + 1 ⊟ x k + 1 ∣ k + 1 = x k + 1 ⊟ x k + 1 ∣ k + 1 κ , δ x κ = x k + 1 ⊟ x k + 1 ∣ k + 1 κ (48) \delta x_{k+1|k+1} = x_{k+1} \boxminus x_{k+1|k+1} = x_{k+1} \boxminus x^{\kappa}{k+1|k+1}, \quad \\ \delta x^{\kappa} = x{k+1} \boxminus x^{\kappa}_{k+1|k+1} \tag{48} δxk+1∣k+1=xk+1⊟xk+1∣k+1=xk+1⊟xk+1∣k+1κ,δxκ=xk+1⊟xk+1∣k+1κ(48)

从而得到

δ x k + 1 ∣ k + 1 = ( x k + 1 ∣ k + 1 κ ⊞ δ x κ ) ⊟ x k + 1 ∣ k + 1 κ = L k + 1 ( δ x κ − δ x κ o ) (49) \delta x_{k+1|k+1} = (x^{\kappa}{k+1|k+1} \boxplus \delta x^{\kappa}) \boxminus x^{\kappa}{k+1|k+1} \\= L_{k+1} (\delta x^{\kappa} - \delta x^o_{\kappa}) \tag{49} δxk+1∣k+1=(xk+1∣k+1κ⊞δxκ)⊟xk+1∣k+1κ=Lk+1(δxκ−δxκo)(49)

其中

L k + 1 = ∂ ( ( ( x ⊕ u ) ⊟ y ) ) ∂ u ∣ x = x k + 1 ∣ k + 1 κ , u = δ x κ o , = ˇ 0 , y = x k + 1 ∣ k + 1 κ (50) L_{k+1} = \frac{\partial \big( ((x \oplus u) \boxminus y) \big)}{\partial u} \Bigg|{x = x^{\kappa}{k+1|k+1}, u = \delta x^o{\kappa}, \v = 0, y = x^{\kappa}_{k+1|k+1}} \tag{50} Lk+1=∂u∂(((x⊕u)⊟y)) x=xk+1∣k+1κ,u=δxκo,=ˇ0,y=xk+1∣k+1κ(50)

是 δ x k + 1 ∣ k + 1 \delta x_{k+1|k+1} δxk+1∣k+1 关于 δ x κ \delta x^{\kappa} δxκ 的雅可比矩阵，在 δ x κ o \delta x^o_{\kappa} δxκo 处求值。最后， δ x k + 1 ∣ k + 1 \delta x_{k+1|k+1} δxk+1∣k+1 的协方差为：

P k + 1 ∣ k + 1 = L k + 1 P k + 1 κ L k + 1 T (51) P_{k+1|k+1} = L_{k+1} P^{\kappa}{k+1} L{k+1}^{T} \tag{51} Pk+1∣k+1=Lk+1Pk+1κLk+1T(51)

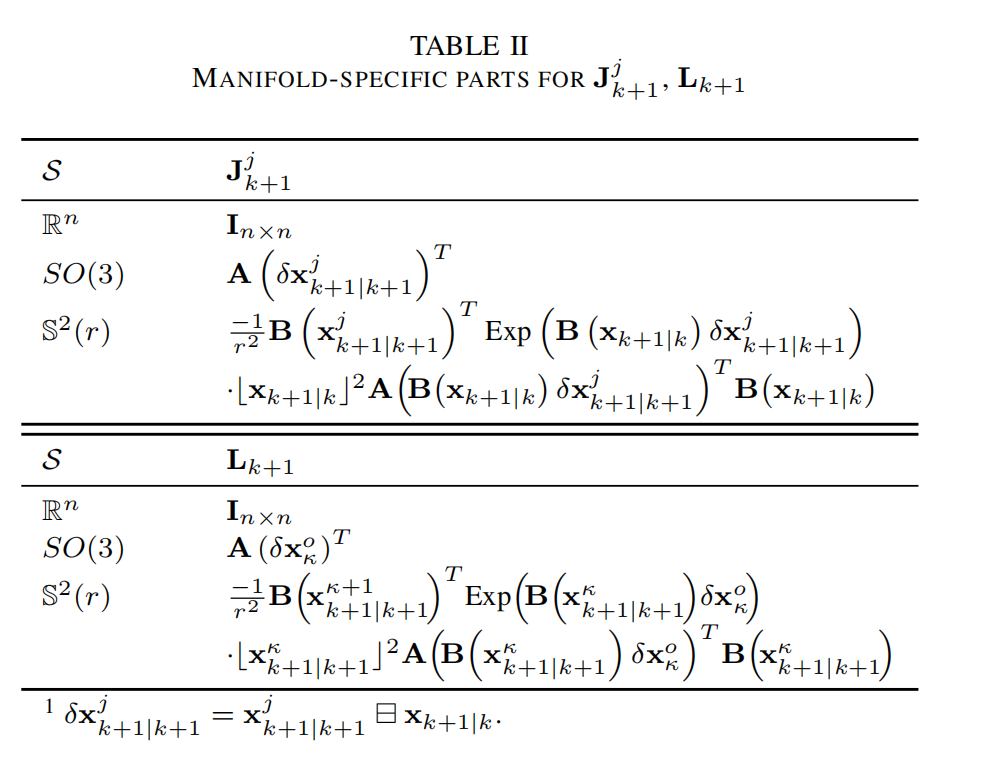
4. 流形结构的隔离 ：注意，Kalman 更新中所需的两个矩阵 J k + 1 j J^j_{k+1} Jk+1j 和 L k + 1 L_{k+1} Lk+1 仅依赖于流形 S S S，因此它们是流形特定的矩阵。常用流形的取值总结如表 II 所示。同样，任何复合流形的流形特定部分都是这些原始流形的拼接。特别地，对于扩展 Kalman 滤波器（即 κ = 0 \kappa = 0 κ=0），有

J k + 1 κ = I , L k + 1 不等于 I J^{\kappa}{k+1} = I, \quad L{k+1} 不等于 I Jk+1κ=I,Lk+1不等于I

而对于完全收敛的迭代 Kalman 滤波器（即 κ \kappa κ 足够大），同样有

J k + 1 κ 不等于 I , L k + 1 = I J^{\kappa}{k+1} 不等于 I, \quad L{k+1} = I Jk+1κ不等于I,Lk+1=I

E. 流形上的误差状态迭代 Kalman 滤波器

总结前面在第 V-A、V-B、V-C 和 V-D 节中介绍的所有步骤，可以得到在流形上运行的完整误差状态迭代 Kalman 滤波器（见算法 1）。将迭代次数 N max ⁡ N_{\max} Nmax 设为零，则得到文献 [6,16] 中使用的误差状态扩展 Kalman 滤波器。

VI. 将流形结构嵌入 Kalman 滤波器并进行工具包开发

正如第 V 节所示，推导出的 Kalman 滤波器以符号化方式给出，并且可以看到 Kalman 滤波器的每一步都被清晰地划分为 流形相关（manifold-specific） 部分与 系统相关（system-specific） 部分。更具体地：

状态传播（公式 (24)） 被拆分为
- 流形相关操作： ⊕ ⊕ ⊕
- 系统相关部分： Δ t f ( x , u , w ) \Delta t f(x, u, w) Δtf(x,u,w)
协方差传播（公式 (35)）中的矩阵 F x F_x Fx 和 F w F_w Fw 被拆分为
- 流形相关部分： G x , G f G_x, G_f Gx,Gf
- 系统相关部分：
  
  ∂ f ( x ⊞ δ x , u , 0 ) ∂ δ x ∣ δ x = 0 , ∂ f ( x , u , w ) ∂ w ∣ w = 0 \left.\frac{\partial f(x \boxplus \delta x, u, 0)}{\partial \delta x}\right|{\delta x = 0}, \qquad \left.\frac{\partial f(x, u, w)}{\partial w}\right|{w = 0} ∂δx∂f(x⊞δx,u,0) δx=0,∂w∂f(x,u,w) w=0
状态更新（公式 (44)） 被拆分为
- 流形相关操作： ⊞ ⊞ ⊞（即文中的符号 ⊞ \boxplus ⊞ 或 ⊟ \boxminus ⊟，此处使用原符号 ⊖ \ominus ⊖ 和 ⊕ \oplus ⊕ 的组合）
- 流形相关部分： J k + 1 j J^{j}_{k+1} Jk+1j
- 系统相关部分，例如：
  
  测量函数 h ( x , v ) h(x, v) h(x,v)
  ∂ ( h ( x ⊞ δ x , 0 ) ⊟ h ( x , 0 ) ) ∂ δ x ∣ δ x = 0 \left.\frac{\partial\left(h(x \boxplus \delta x, 0) \boxminus h(x,0)\right)}{\partial \delta x}\right|{\delta x = 0} ∂δx∂(h(x⊞δx,0)⊟h(x,0)) δx=0
  ∂ ! ( h ( x , v ) ⊟ h ( x , 0 ) ) ∂ v ∣ v = 0 \left.\frac{\partial!\left(h(x, v) \boxminus h(x,0)\right)}{\partial v}\right|{v=0} ∂v∂!(h(x,v)⊟h(x,0)) v=0

协方差重置 仅涉及流形相关部分 L k + 1 L_{k+1} Lk+1。

请注意：即使对于高维机器人系统，这些系统相关部分通常也很容易推导（详见第 VII 节）。

由于流形相关部分与系统相关描述之间的良好分离，使得我们能够将流形结构嵌入到 Kalman 滤波器框架中，而对具体系统而言，只需填写系统相关部分即可。此外，在流形组合（公式 (14) 与 (15)）的支持下，我们只需为基本的原始流形定义相关操作，而较大的复合流形可以自动构建。

基于上述两点，我们开发了一个 C++ 工具包，将流形相关操作与 Kalman 滤波器封装在一起。借助该工具包，用户只需：

指定状态流形 S S S、测量流形 M M M
提供系统相关描述（即函数 f , h f, h f,h 及其导数）
根据当前事件（如接收到控制量或测量）调用相应的 Kalman 滤波器操作（如传播与更新）

目前的工具包实现是一个完整的、可自然运行在流形上的 多频率迭代 Kalman 滤波器（IKF） ，因此称为 IKFoM。工具包支持三类原始流形：

R n \mathbb{R}^n Rn
S O ( 3 ) SO(3) SO(3)
S 2 ( r ) S^2(r) S2(r)

并且可通过适当定义以下内容扩展至其他类型的原始流形：

操作 ⊞ ⊞ ⊞（ ⊟ \boxminus ⊟）、 ⊕ ⊕ ⊕
下列微分项：

∂ ( ( ( x ⊞ u ) ⊕ v ) ⊟ y ) ∂ u \frac{\partial\left( ((x \boxplus u)\oplus v) \boxminus y \right)}{\partial u} ∂u∂(((x⊞u)⊕v)⊟y)
∂ ( ( ( x ⊞ u ) ⊕ v ) ⊟ y ) ∂ v \frac{\partial\left( ((x \boxplus u)\oplus v) \boxminus y \right)}{\partial v} ∂v∂(((x⊞u)⊕v)⊟y)

该工具包已开源，更多实现细节可参考：

https://github.com/hku-mars/IKFoM

后序内容：SLAM文献之-Embedding Manifold Structures into Kalman Filters（3)