一、随机种子
python
import torch
import torch.nn as nn
# 定义简单的线性模型(无隐藏层)
# 输入2个纬度的数据,得到1个纬度的输出
class SimpleNet(nn.Module):
def __init__(self):
super(SimpleNet, self).__init__()
# 线性层:2个输入特征,1个输出特征
self.linear = nn.Linear(2, 1)
def forward(self, x):
# 前向传播:y = w1*x1 + w2*x2 + b
return self.linear(x)
# 创建模型实例
model = SimpleNet()
# 查看模型参数
print("模型参数:")
for name, param in model.named_parameters():
print(f"{name}: {param.data}")
html
模型参数:
linear.weight: tensor([[ 0.3268, -0.5784]])
linear.bias: tensor([0.6189])torch中很多场景都会存在随机数
- 权重、偏置的随机初始化
- 数据加载(shuffling打乱)与批次加载(随机批次加载)的随机化
- 数据增强的随机化(随机旋转、缩放、平移、裁剪等)
- 随机正则化dropout
- 优化器中的随机性
python
import torch
import numpy as np
import os
import random
# 全局随机函数
def set_seed(seed=42, deterministic=True):
"""
设置全局随机种子,确保实验可重复性
参数:
seed: 随机种子值,默认为42
deterministic: 是否启用确定性模式,默认为True
"""
# 设置Python的随机种子
random.seed(seed)
os.environ['PYTHONHASHSEED'] = str(seed) # 确保Python哈希函数的随机性一致,比如字典、集合等无序
# 设置NumPy的随机种子
np.random.seed(seed)
# 设置PyTorch的随机种子
torch.manual_seed(seed) # 设置CPU上的随机种子
torch.cuda.manual_seed(seed) # 设置GPU上的随机种子
torch.cuda.manual_seed_all(seed) # 如果使用多GPU
# 配置cuDNN以确保结果可重复
if deterministic:
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False
# 设置随机种子
set_seed(42)介绍一下这个随机函数的几个部分
python的随机种子,需要确保random模块、以及一些无序数据结构的一致性
numpy的随机种子,控制数组的随机性
torch的随机种子,控制张量的随机性,在cpu和gpu上均适用
cuDNN(CUDA Deep Neural Network library ,CUDA 深度神经网络库)的随机性,针对cuda的优化算法的随机性
二、内参的初始化
先介绍一下神经网络的对称性----为什么神经元的初始值需要各不相同?
本质神经网络的每一个神经元都是在做一件事,输入x--输出y的映射,这里我们假设激活函数是sigmoid
y=sigmoid(wx+b),其中w是连接到该神经元的权重矩阵,b是该神经元的偏置
如果所有神经元的权重和偏置都一样,
-
如果都为0,那么所有神经元的输出都一致,无法区分不同特征;此时反向传播的时候梯度都一样,无法学习到特征,更新后的权重也完全一致。
-
如果不为0,同上
所以,无论初始值是否为 0,相同的权重和偏置会导致神经元在训练过程中始终保持同步。(因为神经网络的前向传播是导致权重的数学含义是完全对称的)具体表现为:
同一层的神经元相当于在做完全相同的计算,无论输入如何变化,它们的输出模式始终一致。例如:输入图像中不同位置的边缘特征,会被这些神经元以相同方式处理,无法学习到空间分布的差异。
所以需要随机初始化,让初始的神经元各不相同。即使初始差异很小,但激活函数的非线性(梯度不同)会放大这种差异。随着训练进行,这种分歧会逐渐扩大,最终形成功能各异的神经元。
避免梯度消失 / 爆炸:
以 sigmoid 激活函数为例,其导数在输入绝对值较大时趋近于 0(如 | x|>5 时,导数≈0)。若初始权重过大,输入 x=w・input+b 可能导致激活函数进入 "饱和区",反向传播时梯度接近 0,权重更新缓慢(梯度消失)。
类比:若初始权重是 "大值",相当于让神经元一开始就进入 "极端状态",失去对输入变化的敏感度。
如果梯度相对较大,就可以让变化处于sigmoid函数的非饱和区
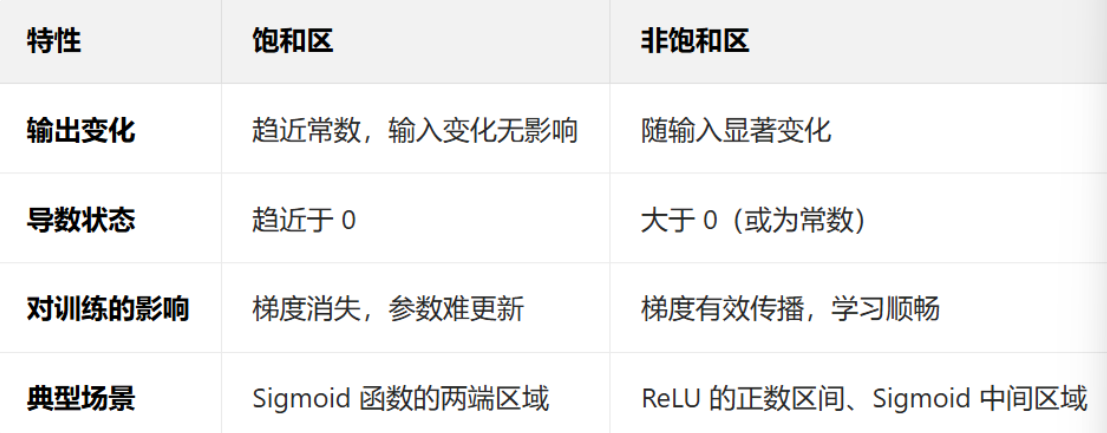
注意下,这里是wx后才会经过激活函数,是多个权重印象的结果,不是收到单个权重决定的,所以单个权重可以取负数,但是如果求和后仍然小于0,那么输出会为0
所以初始值一般不会太大,结合不同激活函数的特性,而且初始值一般是小的值。最终训练完毕可能就会出现大的差异,这样最开始让每个参数都是有用的,至于最后是不是某些参数归0(失去价值),那得看训练才知道。
观察下pytorch默认初始化的权重
python
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import numpy as np
# 设置设备
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
# 定义极简CNN模型(仅1个卷积层+1个全连接层)
class SimpleCNN(nn.Module):
def __init__(self):
super(SimpleCNN, self).__init__()
# 卷积层:输入3通道,输出16通道,卷积核3x3
self.conv1 = nn.Conv2d(3, 16, kernel_size=3, padding=1)
# 池化层:2x2窗口,尺寸减半
self.pool = nn.MaxPool2d(kernel_size=2)
# 全连接层:展平后连接到10个输出(对应10个类别)
# 输入尺寸:16通道 × 16x16特征图 = 16×16×16=4096
self.fc = nn.Linear(16 * 16 * 16, 10)
def forward(self, x):
# 卷积+池化
x = self.pool(self.conv1(x)) # 输出尺寸: [batch, 16, 16, 16]
# 展平
x = x.view(-1, 16 * 16 * 16) # 展平为: [batch, 4096]
# 全连接
x = self.fc(x) # 输出尺寸: [batch, 10]
return x
# 初始化模型
model = SimpleCNN()
model = model.to(device)
# 查看模型结构
print(model)
# 查看初始权重统计信息
def print_weight_stats(model):
# 卷积层
conv_weights = model.conv1.weight.data
print("\n卷积层 权重统计:")
print(f" 均值: {conv_weights.mean().item():.6f}")
print(f" 标准差: {conv_weights.std().item():.6f}")
print(f" 理论标准差 (Kaiming): {np.sqrt(2/3):.6f}") # 输入通道数为3
# 全连接层
fc_weights = model.fc.weight.data
print("\n全连接层 权重统计:")
print(f" 均值: {fc_weights.mean().item():.6f}")
print(f" 标准差: {fc_weights.std().item():.6f}")
print(f" 理论标准差 (Kaiming): {np.sqrt(2/(16*16*16)):.6f}")
# 改进的可视化权重分布函数
def visualize_weights(model, layer_name, weights, save_path=None):
plt.figure(figsize=(12, 5))
# 权重直方图
plt.subplot(1, 2, 1)
plt.hist(weights.cpu().numpy().flatten(), bins=50)
plt.title(f'{layer_name} 权重分布')
plt.xlabel('权重值')
plt.ylabel('频次')
# 权重热图
plt.subplot(1, 2, 2)
if len(weights.shape) == 4: # 卷积层权重 [out_channels, in_channels, kernel_size, kernel_size]
# 只显示第一个输入通道的前10个滤波器
w = weights[:10, 0].cpu().numpy()
plt.imshow(w.reshape(-1, weights.shape[2]), cmap='viridis')
else: # 全连接层权重 [out_features, in_features]
# 只显示前10个神经元的权重,重塑为更合理的矩形
w = weights[:10].cpu().numpy()
# 计算更合理的二维形状(尝试接近正方形)
n_features = w.shape[1]
side_length = int(np.sqrt(n_features))
# 如果不能完美整除,添加零填充使能重塑
if n_features % side_length != 0:
new_size = (side_length + 1) * side_length
w_padded = np.zeros((w.shape[0], new_size))
w_padded[:, :n_features] = w
w = w_padded
# 重塑并显示
plt.imshow(w.reshape(w.shape[0] * side_length, -1), cmap='viridis')
plt.colorbar()
plt.title(f'{layer_name} 权重热图')
plt.tight_layout()
if save_path:
plt.savefig(f'{save_path}_{layer_name}.png')
plt.show()
# 打印权重统计
print_weight_stats(model)
# 可视化各层权重
visualize_weights(model, "Conv1", model.conv1.weight.data, "initial_weights")
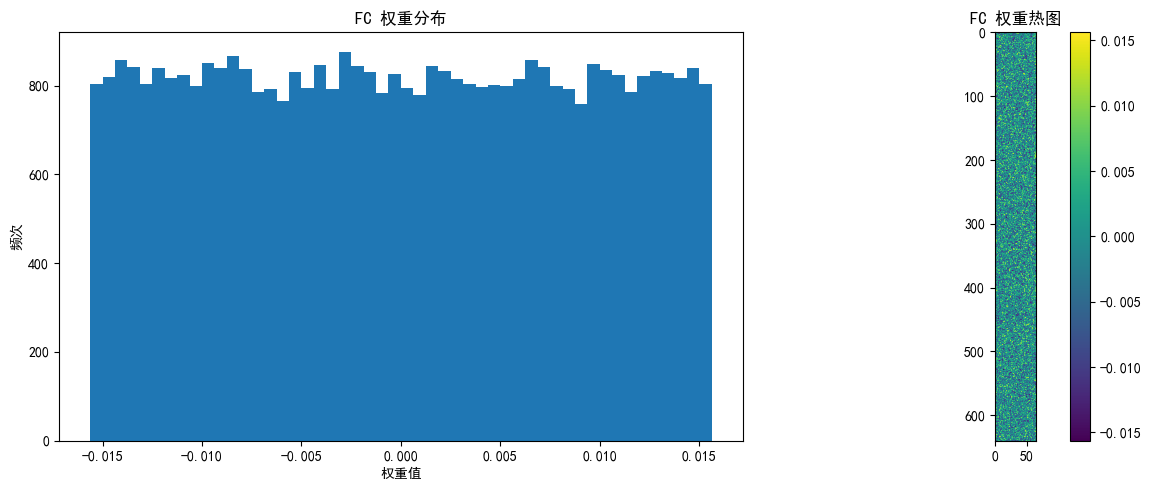
visualize_weights(model, "FC", model.fc.weight.data, "initial_weights")
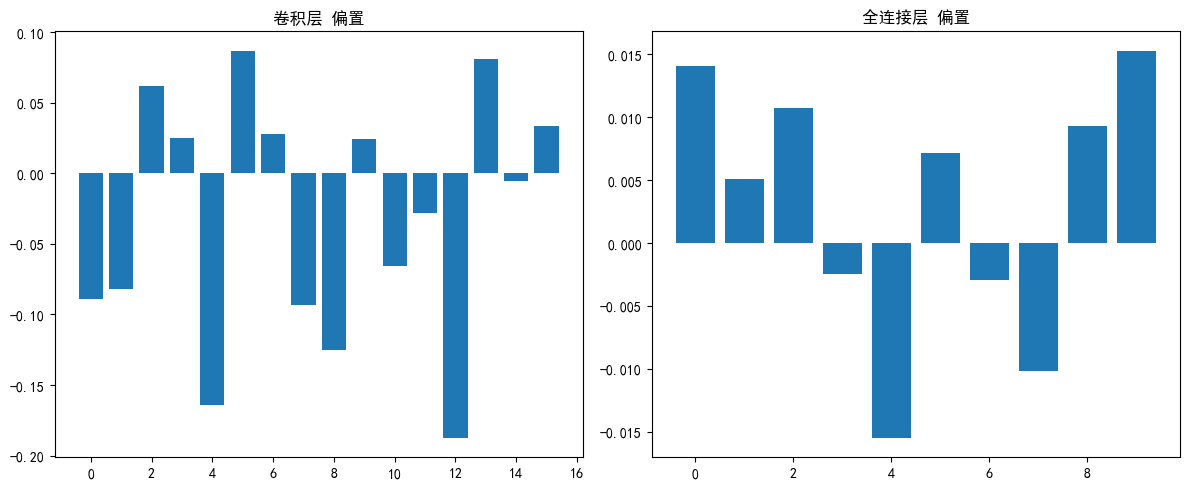
# 可视化偏置
plt.figure(figsize=(12, 5))
# 卷积层偏置
conv_bias = model.conv1.bias.data
plt.subplot(1, 2, 1)
plt.bar(range(len(conv_bias)), conv_bias.cpu().numpy())
plt.title('卷积层 偏置')
# 全连接层偏置
fc_bias = model.fc.bias.data
plt.subplot(1, 2, 2)
plt.bar(range(len(fc_bias)), fc_bias.cpu().numpy())
plt.title('全连接层 偏置')
plt.tight_layout()
plt.savefig('biases_initial.png')
plt.show()
print("\n偏置统计:")
print(f"卷积层偏置 均值: {conv_bias.mean().item():.6f}")
print(f"卷积层偏置 标准差: {conv_bias.std().item():.6f}")
print(f"全连接层偏置 均值: {fc_bias.mean().item():.6f}")
print(f"全连接层偏置 标准差: {fc_bias.std().item():.6f}")
html
SimpleCNN(
(conv1): Conv2d(3, 16, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(pool): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(fc): Linear(in_features=4096, out_features=10, bias=True)
)
卷积层 权重统计:
均值: -0.005068
标准差: 0.109001
理论标准差 (Kaiming): 0.816497
全连接层 权重统计:
均值: -0.000031
标准差: 0.009038
理论标准差 (Kaiming): 0.022097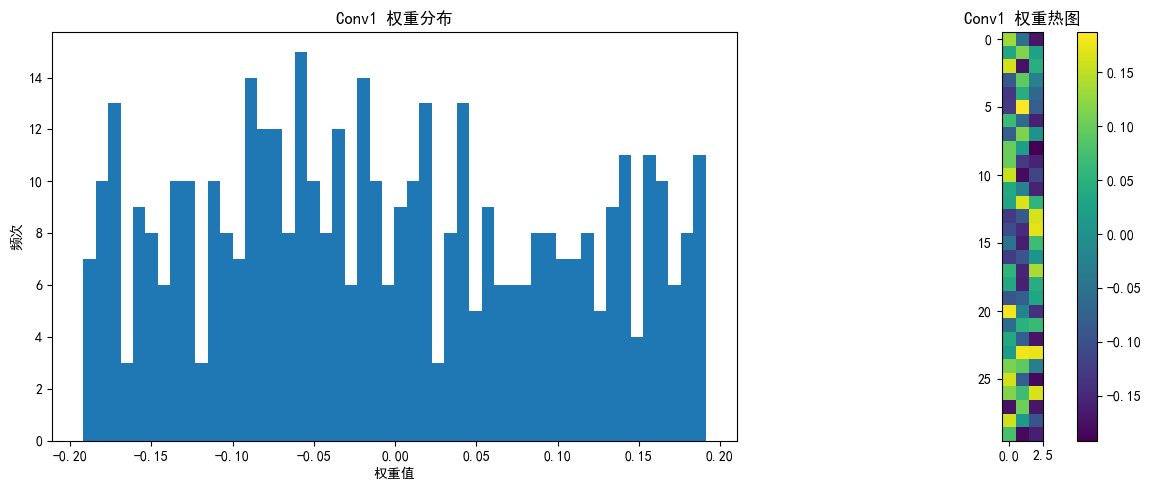
三、神经网络调参指南
3.1 参数的分类
通常可以将超参数分为三类:网络参数、优化参数、正则化参数。
**网络参数:**包括网络层之间的交互方式(如相加、相乘或串接)、卷积核的数量和尺寸、网络层数(深度)和激活函数等。
**优化参数:**一般指学习率、批样本数量、不同优化器的参数及部分损失函数的可调参数。
**正则化参数:**如权重衰减系数、丢弃比率(dropout)。
超参数调优的目的是优化模型,找到最优解与正则项之间的关系。网络模型优化的目的是找到全局最优解(或相对更好的局部最优解),而正则项则希望模型能更好地拟合到最优。两者虽然存在一定对立,但目标是一致的,即最小化期望风险。模型优化希望最小化经验风险,但容易过拟合,而正则项用来约束模型复杂度。因此,如何平衡两者关系,得到最优或较优的解,就是超参数调整的目标。
3.2 调参顺序
调参遵循 "先保证模型能训练(基础配置)→ 再提升性能(核心参数)→ 最后抑制过拟合(正则化)" 的思路,类似 "先建框架,再装修,最后修细节"。
下面顺序建立在已经跑通了的基础上。
参数初始化----有预训练的参数直接起飞
batchsize---测试下能允许的最高值
epoch---这个不必多说,默认都是训练到收敛位置,可以采取早停策略
学习率与调度器----收益最高,因为鞍点太多了,模型越复杂鞍点越多
模型结构----消融实验或者对照试验
损失函数---选择比较少,试出来一个即可,高手可以自己构建
激活函数---选择同样较少
正则化参数---主要是droupout,等到过拟合了用,上述所有步骤都为了让模型过拟合
这个调参顺序并不固定,而且也不是按照重要度来选择,是按照方便程度来选择,比如选择少的选完后,会减小后续实验的成本。
3.3 初始化参数
预训练参数是最好的参数初始化方法,在训练前先找找类似的论文有无预训练参数,其次是Xavir,尤其是小数据集的场景,多找论文找到预训练模型是最好的做法。关于预训练参数,我们介绍过了,优先动深层的参数,因为浅层是通用的;其次是学习率要采取分阶段的策略。
如果从0开始训练的话,PyTorch 默认用 Kaiming 初始化(适配 ReLU)或 Xavier 初始化(适配 Sigmoid/Tanh)。
3.4 bitchsize的选择
当Batch Size 太小的时候,模型每次更新学到的东西太少了,很可能白学了因为缺少全局思维。所以尽可能高一点,16的倍数即可,越大越好。
3.5 学习率调整
学习率就是参数更新的步长,LR 过大→不好收敛;LR 过小→训练停滞(陷入局部最优)
一般最开始用adam快速收敛,然后sgd收尾,一般精度会高一点;只能选一个就adam配合调度器使用。比如 CosineAnnealingLR余弦退火调度器、StepLR固定步长衰减调度器,比较经典的搭配就是Adam + ReduceLROnPlateau,SGD + CosineAnnealing,或者Adam → SGD + StepLR。
3.6 激活函数的选择
视情况选择,一般默认relu或者其变体,如leaky relu,再或者用tanh。只有二分类任务最后的输出层用sigmoid,多分类任务用softmax,其他全部用relu即可。此外,还有特殊场景下的,比如GELU(适配 Transformer)
3.7 损失函数的选择
大部分我们目前接触的任务都是单个损失函数构成的,正常选即可
分类任务:
交叉熵损失函数Cross-Entropy Loss--多分类场景
二元交叉熵损失函数Binary Cross-Entropy Loss--二分类场景
Focal Loss----类别不平衡场景
注意点:
- CrossEntropyLoss内置 Softmax,输入应为原始 logits(非概率)。
- BCEWithLogitsLoss内置 Sigmoid,输入应为原始 logits。
- 若评价指标为准确率,用交叉熵损失;若为 F1 分数,考虑 Focal Loss 或自定义损失。
回归任务
均方误差MSE
绝对误差MAE
这个也要根据场景和数据特点来选,不同损失受到异常值的影响程度不同
3.8 模型架构中的参数
比如卷积核尺寸等,一般就是7*7、5*5、3*3这种奇数对构成,其实我觉得无所谓,最开始不要用太过分的下采样即可。
神经元的参数,直接用 Kaiming 初始化(适配 ReLU,PyTorch 默认)或 Xavier 初始化(适配 Sigmoid/Tanh)。
3.9 正则化系数
droupout一般控制在0.2-0.5之间,这里说一下小技巧,先追求过拟合后追求泛化性。也就是说先把模型做到过拟合,然后在慢慢增加正则化程度。
正则化中,如果train的loss可以很低,但是val的loss还是很高,则说明泛化能力不强,优先让模型过拟合,在考虑加大正则化提高泛化能力,可以分模块来droupout,可以确定具体是那部分参数导致过拟合,这里还有个小trick是引入残差链接后再利用droupout
勇闯python的第51天@浙大疏锦行