感知机(Perceptron)算法详解及代码
一、算法定位
- 学习类型:监督学习
- 任务类型:二分类
- 模型性质:线性分类模型
- 标签取值 :
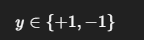
感知机的目标是学习一个线性判别函数,将两类样本正确分开。
二、模型表达式(判别函数)
感知机的判别函数为:
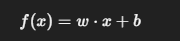
- (w):权重向量
- (b):偏置
- 判别规则:
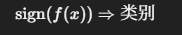
三、分类正确与误分类判据
对于样本 ((x_i, y_i)):
-
分类正确 :
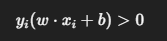
-
分类错误 :
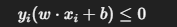
感知机的学习过程完全围绕这一判据展开。
四、损失函数设计(核心思想)
感知机采用误分类驱动的损失函数,仅对误分类样本定义损失:
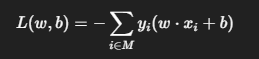
其中:
- (M):误分类样本集合
- 分类正确的样本损失为 0,不参与优化
特点:
- 损失函数不连续
- 不引入概率模型
- 只关心分类是否正确,不关心分类"置信度"
五、参数优化方法
感知机使用随机梯度下降(SGD)思想,但仅在误分类样本上更新参数。
1️⃣ 单样本损失函数
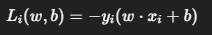
2️⃣ 梯度计算
-
对权重:
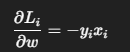
-
对偏置:
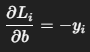
六、参数更新公式(优化公式来源)
根据梯度下降法:
-
权重更新 :
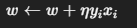
-
偏置更新 :
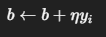
其中:
- n:学习率
关键特性:
- 只有当样本被误分类时,才进行参数更新
- 分类正确时,不计算损失,也不进行"反向传播"
七、算法流程
- 初始化参数 (w=0, b=0)
- 依次遍历训练样本
- 若样本被误分类,则更新 (w, b)
- 若一轮训练中无任何误分类样本,则算法停止
八、几何意义
- 感知机学习的是一个线性可分超平面
- 参数更新的本质是调整超平面的位置和方向
- 更新方向由误分类样本及其标签决定
- 不显式最大化分类间隔
九、重要性质
- 感知机收敛定理 :
若训练数据线性可分,感知机在有限步内必然收敛 - 若数据线性不可分,感知机可能永不停止
十、与其他模型的核心区别
| 模型 | 是否使用概率 | 是否所有样本参与优化 |
|---|---|---|
| 感知机 | 否 | 否(仅误分类样本) |
| 逻辑回归 | 是 | 是 |
| SVM | 否 | 部分 |
| 神经网络 | 是 | 是 |
十一. 代码
python
import numpy as np
class Perceptron:
def __init__(self, learning_rate=0.1, max_iter=1000):
self.learning_rate = learning_rate
self.max_iter = max_iter
self.w = None
self.b = 0
def fit(self, X, y):
# 初始化权重
self.w = np.zeros(X.shape[1])
# 迭代训练
for _ in range(self.max_iter):
misclassified = 0
for xi, yi in zip(X, y):
# 误分类判定
if yi * (np.dot(self.w, xi) + self.b) <= 0:
# 参数更新(带学习率)
self.w = self.w + self.learning_rate * yi * xi
self.b = self.b + self.learning_rate * yi
misclassified += 1
# 若一轮中无误分类样本,则停止
if misclassified == 0:
break
def predict(self, X):
return np.sign(np.dot(X, self.w) + self.b)