今天我们要聊的是一个改变了世界的算法------PageRank。
它的名字里虽然有个"Page",但它不仅仅是指"网页 (Web Page)",更是以它的发明者之一、Google 的创始人 拉里·佩奇 (Larry Page) 的名字命名的。
正是这个算法,让 Google 在当年众多的搜索引擎中脱颖而出,成为了今天的巨头。
如果你完全不懂算法,没关系。想象一下,你正在竞选**"班级最受欢迎人物"**。
1. 核心思想:谁给我投票?
在 PageRank 出现之前,搜索引擎判断一个网页重不重要,主要是看**"关键词出现了多少次"**。
这就像是选班长,谁嗓门大、谁喊口号喊得多,谁就赢。这显然不合理,容易被作弊。
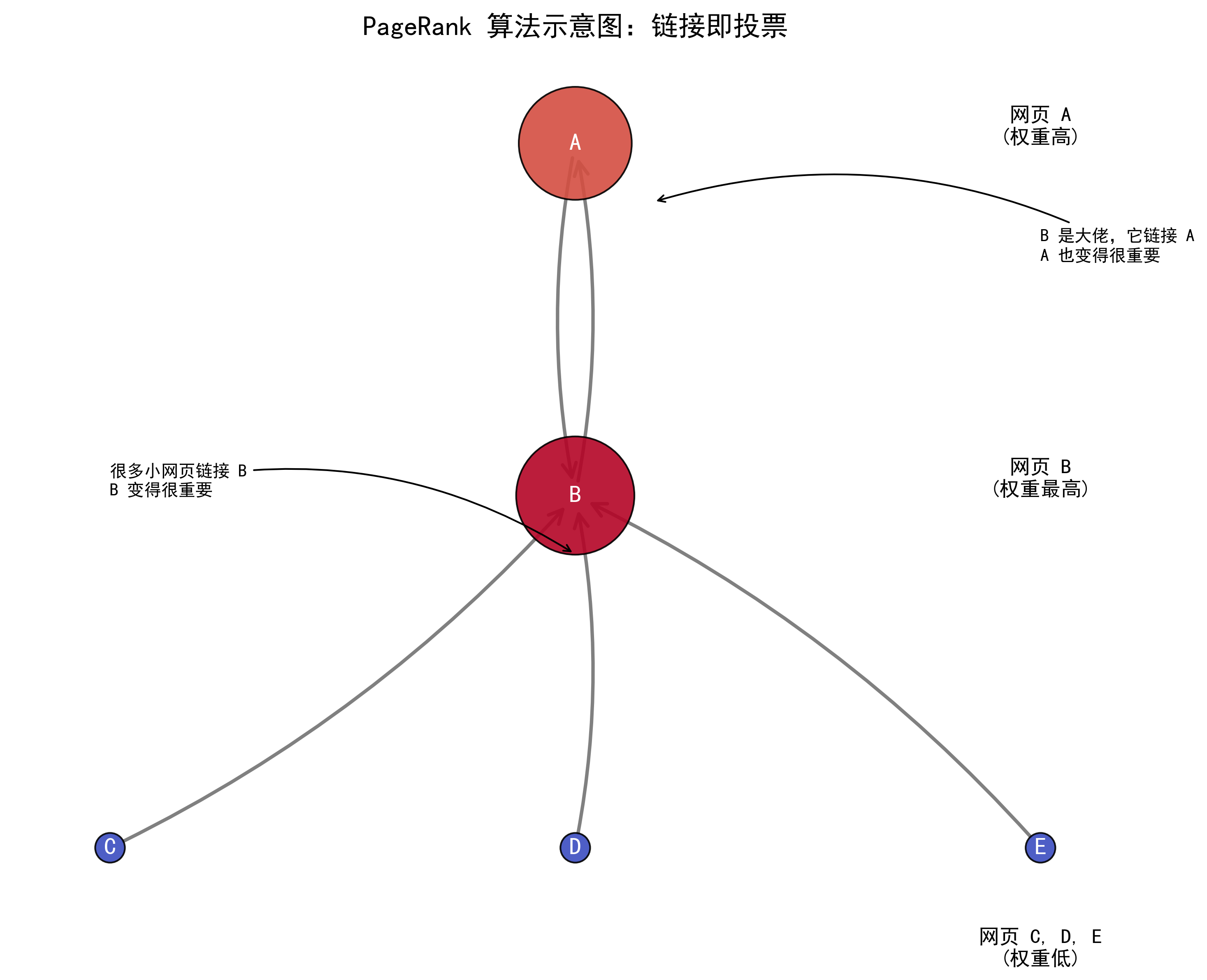
PageRank 引入了一个全新的逻辑:看谁给你投票!
在互联网上,一个链接 (Link) 就相当于一张选票。
- 如果网页 A 链接到了网页 B,就相当于 A 投了 B 一票。
但是,PageRank 的精髓在于:不是所有的票都一样值钱。
2. 两个关键规则
规则一:票数越多越好 (数量)
这很好理解。如果有很多网页都链接向你(给你投票),说明你很受欢迎,你的排名就应该靠前。
规则二:大佬的票更值钱 (质量)
这是 PageRank 最天才的地方。
- 场景 A:隔壁班的小透明张三投了你一票。
- 场景 B:全校公认的校草/校花投了你一票。
显然,场景 B 的这一票含金量更高!
在网页世界里也是一样:
- 如果一个不知名的小博客链接了你,你的权重增加一点点。
- 如果 Wikipedia (维基百科) 或者 Yahoo 链接了你,你的权重会暴涨。
总结一句话:一个网页的权重,取决于链接它的那些网页的权重。
3. 它是怎么算的?(举个栗子)
假设互联网上只有 4 个网页:A, B, C, D 。
为了演示,我们设定它们的链接关系如下:
- A 链接 -> B, C, D (A 很大方,谁都投)
- B 链接 -> A (B 只喜欢 A)
- C 链接 -> A, B (C 喜欢 A 和 B)
- D 链接 -> A, B, C (D 喜欢大家,除了自己)
初始状态 :大家权重一样,都是 1 分。
第 1 轮结算 (简化版,不带阻尼系数)
- A 的得分 :
- B 全给它 (1/1) + C 给一半 (1/2) + D 给三分之一 (1/3)
- 1 + 0.5 + 0.33 ≈ 1.83
- B 的得分 :
- A 给三分之一 (1/3) + C 给一半 (1/2) + D 给三分之一 (1/3)
- 0.33 + 0.5 + 0.33 ≈ 1.17
- C 的得分 :
- A 给三分之一 (1/3) + D 给三分之一 (1/3)
- 0.33 + 0.33 ≈ 0.67
- D 的得分 :
- A 给三分之一 (1/3)
- 0.33 ≈ 0.33
(注:1.83+1.17+0.67+0.33 = 4.0,总分守恒)
第 2 轮结算 (用第 1 轮的分数继续算)
这时候,B 的权重变成了 1.17,它投给 A 的那一票更值钱了!
- A 的得分 :
- B(1.17)全给 + C(0.67)给一半 + D(0.33)给三分之一
- 1.17 + 0.335 + 0.11 ≈ 1.615
- B 的得分 :
- A(1.83)给三分之一 + C(0.67)给一半 + D(0.33)给三分之一
- 0.61 + 0.335 + 0.11 ≈ 1.055
- C 的得分 :
- A(1.83)给三分之一 + D(0.33)给三分之一
- 0.61 + 0.11 ≈ 0.72
- D 的得分 :
- A(1.83)给三分之一
- 0.61 ≈ 0.61
第 3 轮结算
- A 的得分 :
- B(1.055)全给 + C(0.72)给一半 + D(0.61)给三分之一
- 1.055 + 0.36 + 0.20 ≈ 1.615 (趋于稳定)
- B 的得分 :
- A(1.615)给三分之一 + C(0.72)给一半 + D(0.61)给三分之一
- 0.54 + 0.36 + 0.20 ≈ 1.10
- C 的得分 :
- A(1.615)给三分之一 + D(0.61)给三分之一
- 0.54 + 0.20 ≈ 0.74
- D 的得分 :
- A(1.615)给三分之一
- 0.54 ≈ 0.54
结论 :
你会发现,经过几轮迭代,A 始终是老大 (因为大家都投它),B 是老二 (因为老大 A 和老三 C 都投它)。
PageRank 算法就是这样一轮一轮地算,直到大家的权重都稳定下来。
4. 随机浏览者 (Random Surfer) 与 阻尼系数
你可能会问:"如果有一群网页互相链接,形成一个小圈子,权重岂不是会无限循环累加?"
或者:"如果一个网页只有进去的链接,没有出去的链接(黑洞),权重岂不是只进不出?"
为了解决这个问题,PageRank 引入了一个**"随机浏览者"**模型。
想象一个人在上网,他大部分时间是顺着链接点点点。
但是,他也有可能突然厌烦了 ,关掉当前页面,随机输入一个新网址飞走了。
这个"飞走"的概率,通常设定为 0.15 (也就是 15% 的概率飞走,85% 的概率继续点链接)。
这个 0.85 就叫做阻尼系数 (Damping Factor)。
它保证了即使是小圈子或者黑洞,权重也会通过"随机跳转"分配给整个互联网的其他角落,避免了死循环。
5. PageRank 的优缺点
✅ 优点 (为什么它伟大?)
- 抗作弊:你很难伪造大量"高质量"的外部链接(大佬不会随便理你)。单纯堆砌关键词没用了。
- 全局视角:它利用了整个互联网的结构信息,而不是只看单个网页的内容。
❌ 缺点 (也要注意)
- 计算量大:互联网有几百亿个网页,算一次矩阵乘法非常耗时(虽然现在有各种优化)。
- 对新网页不友好:新网页刚诞生,没人链接它,就算内容再好,PageRank 也会很低(需要时间积累)。
6. 总结
PageRank 就是互联网世界的**"人脉评估系统"**:
- 链接 = 投票。
- 权重 = 影响力。
- 你的人脉越广、给你背书的大佬越牛,你的地位就越高。
虽然现在的搜索引擎算法已经非常复杂(加入了用户行为、内容质量、AI 语义理解等),但 PageRank 依然是那个奠定基石的经典思想!🕸️