[算法设计与分析-从入门到入土] 图遍历

个人导航

知乎：https://www.zhihu.com/people/byzh_rc

CSDN：https://blog.csdn.net/qq_54636039

注：本文仅对所述内容做了框架性引导，具体细节可查询其余相关资料or源码

参考文章：各方资料

文章目录

[[算法设计与分析-从入门到入土] 图遍历](#[算法设计与分析-从入门到入土] 图遍历)
个人导航
[图遍历Graph Traversal](#图遍历Graph Traversal)
- - - 1.深度优先搜索DFS
    - 2.广度优先搜索BFS
[寻找图中的关节点Articulation Point](#寻找图中的关节点Articulation Point)

图遍历Graph Traversal

图遍历的核心目标是访问图中所有顶点，主要有两种经典方法：

深度优先搜索（Depth-first Search, DFS）
广度优先搜索（Breadth-first Search, BFS）

1.深度优先搜索DFS

设 G = ( V , E ) G=(V,E) G=(V,E) 为一个有向图或无向图

初始化：将图中所有顶点标记为「未访问」状态
选择起始顶点：任选一个顶点 v∈V，将其标记为「已访问」
深度探索：取与 v 相邻的未访问顶点 w，标记为「已访问」，并继续探索与 w 相邻的未访问顶点 x，重复此过程
回溯：当遇到顶点 y（其所有相邻顶点均已访问）时，回溯至上一个已访问顶点（如 x），若该顶点有未访问的相邻顶点，则继续探索
终止：最终回溯至起始顶点 v，遍历结束

DFS可通过递归方式实现

例子:

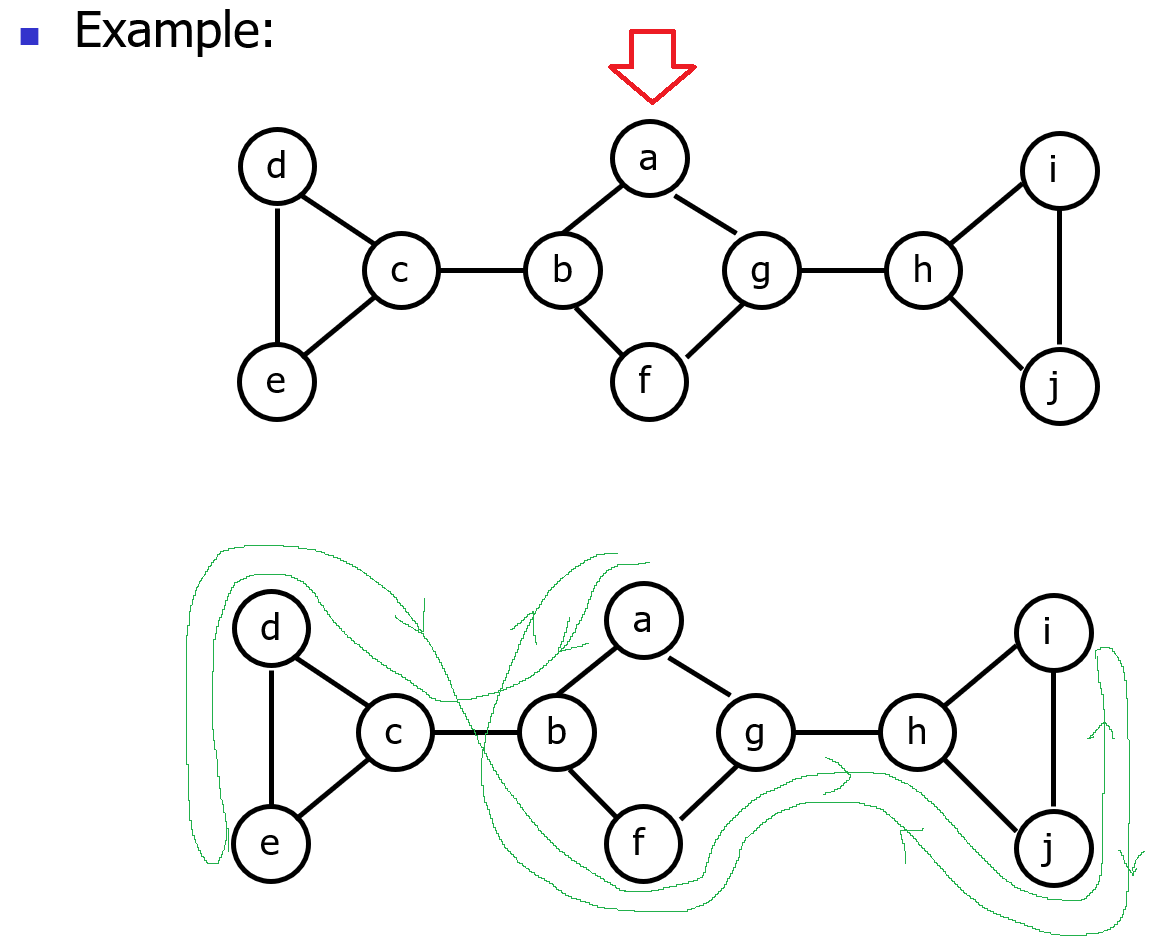
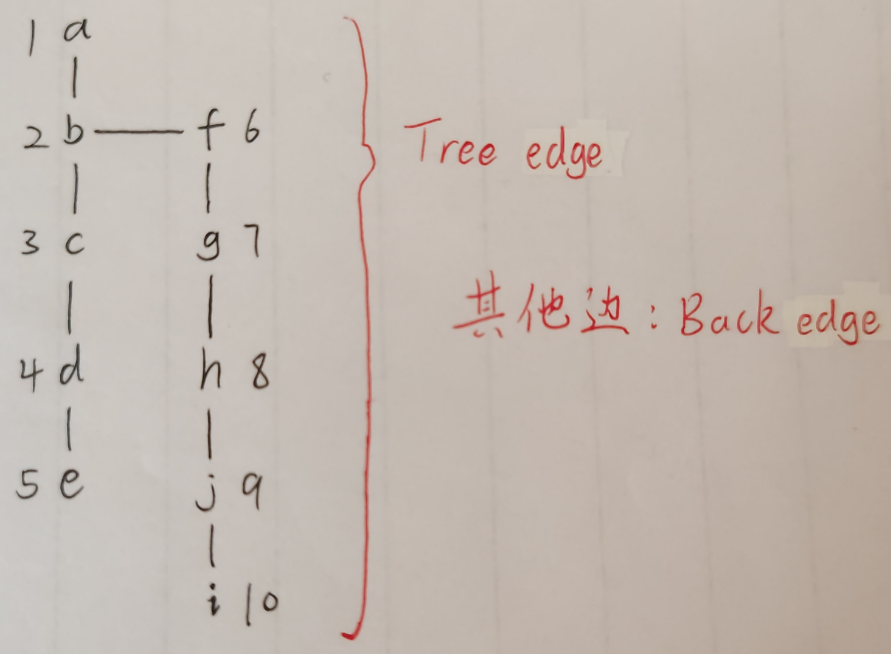
若 DFS 完成后所有顶点均可从起始顶点到达，会构建出「深度优先搜索生成树」（简称 DFS 生成树）

此时无向图 G 的边可划分为两类：

树边（tree edge）：属于 DFS 生成树的边
回边（back edge）：不属于生成树的其他边

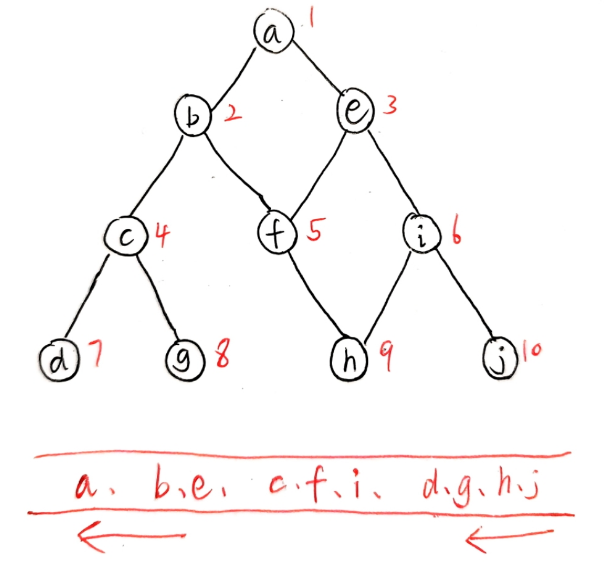
2.广度优先搜索BFS

当访问一个顶点 v 时，接下来会优先访问所有与 v 直接相邻的顶点

通过「队列」数据结构存储未检查的顶点：

初始化：标记所有顶点为「未访问」，将起始顶点 v 标记为「已访问」并加入队列
出队访问：将队首顶点 u 出队，遍历其所有相邻顶点
入队标记：对每个未访问的相邻顶点，标记为「已访问」并加入队列
重复：直至队列为空，遍历结束

例子:

寻找图中的关节点Articulation Point

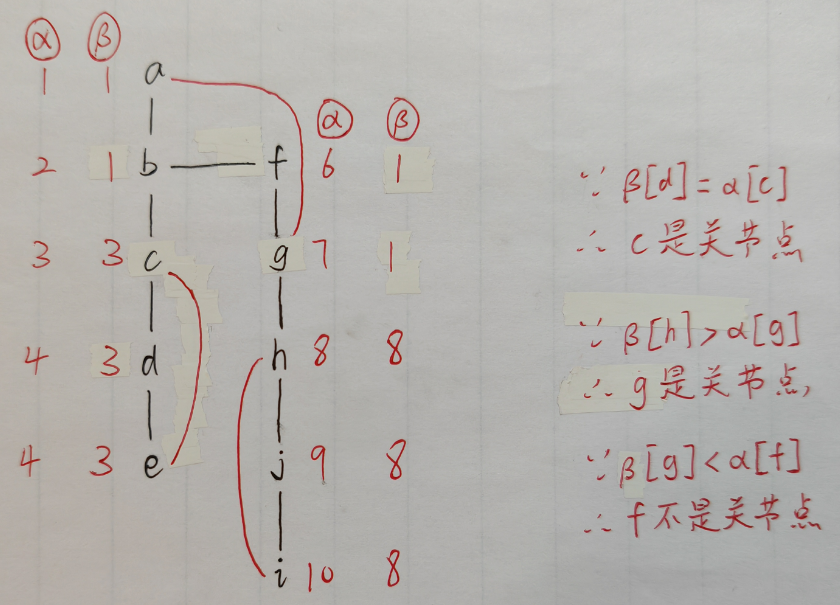
在无向图 G 中（含多个顶点），若存在两个不同于 v 的顶点 u 和 w，使得 u 与 w 之间的所有路径都必须经过 v，则顶点 v 称为「关节点」（也叫割点）

若移除顶点 v 及其关联的所有边，原本连通的图 G 会变为不连通的子图，则 v 是关节点

若一个连通图没有关节点，则称该图为「双连通图」

基于 DFS 寻找关节点:

α [ v ] α[v] α[v]：顶点 v 的「访问顺序」
（即 DFS 过程中首次访问 v 时的时间戳）
β [ v ] β[v] β[v]：顶点 v 能通过「回边」到达的「最早祖先节点」的访问顺序
（初始时 β [ v ] = α [ v ] β[v] = α[v] β[v]=α[v]，遍历中动态更新）

遍历过程中， β [ v ] β[v] β[v] 取以下三者的最小值:
β [ v ] = m i n { α [ v ] , α [ 父节点 w ] , β [ 子节点 u ] } \beta[v] = min\{ \alpha[v], \alpha[\text{父节点}w], \beta[\text{子节点}u] \} β[v]=min{α[v],α[父节点w],β[子节点u]}
例子: