atcoder ABC438 题解

atcoder abc#438 题解

A - 新年第一场比赛

时间限制：2 秒

内存限制：1024 MiB

分值：100 分

题目描述

在某颗星球上，一年有 DDD 天，并且每 7 天 举办一次比赛。比赛的举办时间不会跨天。某一年的第一场比赛在该年的第 FFF 天举办。请问，下一年的第一场比赛会在次年的第几天举办？

题目保证：下一年至少会举办一场比赛。

数据范围

10≤D≤36610 \le D \le 36610≤D≤366 1≤F≤71 \le F \le 71≤F≤7 所有输入均为整数

解题思路

做法1：在 F 的基础上不停的加 7，直到 F 大于 D 为止，然后计算下 F 和 D 的差值。

做法2：（D - F）% 7 即为第一年最后一次比赛后，剩下的天数，再拿 7 做一下差即可。

代码

cpp 复制代码

#include <bits/stdc++.h>

using namespace std;

const int maxn = 5e6 + 5;
int d, f;

int main()
{
    cin >> d >> f;
    d -= f; // 做差
    int ans = 7;
    cout << ans - d % 7; 
    return 0;
}

B - 子串 2

时间限制：2 秒

内存限制：1024 MiB

分值：200 分

题目描述

给定整数 N 和 M，以及一个长度为 N 的数字串 S、一个长度为 M 的数字串 T。（注：数字串指仅由 0~9 的数字构成的字符串）你可以执行零次或多次以下操作：

选择 T 中的一个字符，将其对应的数字加 1。特别地，若被选数字为 9，则将其变为 0。请你求出，要使 T 成为 S 的子串（连续子序列），至少需要执行多少次操作。

数据范围

1 ≤ M ≤ N ≤ 100，N、M 均为整数，S 是长度为 N 的数字串，T 是长度为 M 的数字串。

解题思路

因为 M 和 N 都特别的小，所以我们可以首先枚举 S 的子串（具体来说是子串的第一个位置），然后计算每一个位置需要的操作数，求和即可。

代码

cpp 复制代码

#include <bits/stdc++.h>

using namespace std;

const int maxn = 5e6 + 5;
string s, t;

int main()
{
    int n, m;
    cin >> n >> m;
    cin >> s >> t;
    int ans = 0x3f3f3f3f; // 最终答案
    for (int i = 0; i <= s.size() - t.size(); i++) // 枚举子串开始位置
    {
        int dis = 0; // 求操作数之和
        for (int j = 0; j < t.size(); j++)
        {
            int a = s[i + j] - '0', b = t[j] - '0';
            dis += (a + 10 - b) % 10; // 从 b 变成 a 需要多少次操作
        }
        ans = min(ans, dis); // 别忘了是在所有子串里面找一个最好的
    }
    cout << ans;
    return 0;
}

C - 一维泡泡龙

时间限制：2 秒

内存限制：1024 MiB

分值：300 分

题目描述

给定一个长度为 NNN 的整数序列 A=(A1,A2,...,AN)A = (A_1, A_2, \dots, A_N)A=(A1,A2,...,AN)。你可以以任意顺序执行零次或多次以下操作：

选择一个满足 1≤k≤∣A∣−31 \le k \le |A| - 31≤k≤∣A∣−3 的整数 kkk，要求 Ak=Ak+1=Ak+2=Ak+3A_k = A_{k+1} = A_{k+2} = A_{k+3}Ak=Ak+1=Ak+2=Ak+3，然后将 Ak,Ak+1,Ak+2,Ak+3A_k,A_{k+1},A_{k+2},A_{k+3}Ak,Ak+1,Ak+2,Ak+3 从序列 AAA 中移除。（更严谨地说，执行操作后序列 AAA 会被替换为 (A1,A2,...,Ak−1,Ak+4,Ak+5,...,A∣A∣)(A_1, A_2, \dots, A_{k-1}, A_{k+4}, A_{k+5}, \dots, A_{|A|})(A1,A2,...,Ak−1,Ak+4,Ak+5,...,A∣A∣)）其中 ∣A∣|A|∣A∣ 表示当前序列 AAA 的长度。

请你求出，经过若干次操作后，序列 AAA 的长度可能的最小值。

数据范围

1≤N≤2×1051 \le N \le 2 \times 10^51≤N≤2×105

1≤Ai≤N1 \le A_i \le N1≤Ai≤N

所有输入均为整数

解题思路

利用栈模拟整个过程，我们从左到右依次将元素添加到栈顶，如果发现在栈顶有连续四个一样的元素，那么我们就删除。这样的话，后面的新元素就可以和前面的相同元素进行匹配。

记录删除了多少次，最后输出 n - 4 * cnt 即可（cnt 为删除次数）。

代码

cpp 复制代码

#include <bits/stdc++.h>

using namespace std;

const int maxn = 5e6 + 5;
int stk[maxn], n, top; // stk 是栈容器，top 是模拟的栈顶指针

int main()
{
    cin >> n;
    int ans = n;
    for (int i = 1; i <= n; i++) 
    {
        int x;
        cin >> x;
        stk[++top] = x; // 添加一个新元素进去
        if (top >= 4 && stk[top] == stk[top - 1] && stk[top - 1] == stk[top - 2] && stk[top - 2] == stk[top - 3]) // 看看是不是连续四个相同的，不过要注意不要越界
            ans -= 4, top -= 4; // 记录答案，把栈顶元素删除
    }
    cout << ans;
    return 0;
}

D - 蛇尾

时间限制：2 秒

内存限制：1024 MiB

分值：400 分

题目描述

Snuke 正在观察一条蛇，他对蛇的头部、身体和尾部的划分方式感到好奇。

他将这条蛇分成了 NNN 个区块，并分别评估了每个区块的头部相似度 、身体相似度 和尾部相似度。现在，他想要找到一种划分方式，使得所有区块的相似度总和最大。

给定三个长度为 NNN 的整数序列 A=(A1,A2,...,AN)A = (A_1,A_2,\dots,A_N)A=(A1,A2,...,AN)、B=(B1,B2,...,BN)B = (B_1,B_2,\dots,B_N)B=(B1,B2,...,BN)、C=(C1,C2,...,CN)C = (C_1,C_2,\dots,C_N)C=(C1,C2,...,CN)。

请你找到满足条件 1≤x<y<N1 \le x < y < N1≤x<y<N 的整数对 (x,y)(x,y)(x,y)，使得下式的值最大：

∑i=1xAi+∑i=x+1yBi+∑i=y+1NCi\sum_{i=1}^{x}A_i + \sum_{i=x+1}^{y}B_i + \sum_{i=y+1}^{N}C_ii=1∑xAi+i=x+1∑yBi+i=y+1∑NCi

数据范围

3≤N≤3×1053 \le N \le 3 \times 10^53≤N≤3×105

1≤Ai,Bi,Ci≤1061 \le A_i,B_i,C_i \le 10^61≤Ai,Bi,Ci≤106

所有输入均为整数。

解题思路

在没有修改，并且要求区间和的要求下，我们首先应该能想到前缀和，那么这里我们用三个数组 a、 b、 c 来表示 A、B、C 的前缀和数组，当我们确定出 x 和 y 的值之后，就有：

∑i=1xAi+∑i=x+1yBi+∑i=y+1NCi=ax+by−bx+cN−cy=(ax−bx)+(by−cy)+cn\sum_{i=1}^{x}A_i + \sum_{i=x+1}^{y}B_i + \sum_{i=y+1}^{N}C_i = a_x + b_y - b_x + c_N - c_y = (a_x - b_x) + (b_y - c_y) + c_ni=1∑xAi+i=x+1∑yBi+i=y+1∑NCi=ax+by−bx+cN−cy=(ax−bx)+(by−cy)+cn

所以我们在枚举 y 的位置的同时，维护前面 (ax−bx)(a_x - b_x)(ax−bx) 的最大值即可。

代码

cpp 复制代码

#include <bits/stdc++.h>
#define int long long

using namespace std;

const int maxn = 3e5 + 5, INF = 1e12;
int n, a[maxn], b[maxn], c[maxn];

signed main()
{
    cin >> n;
    a[0] = b[0] = c[0] = 0;
    for (int i = 1; i <= n; i++)
    {
        int x;
        cin >> x;
        a[i] = a[i - 1] + x;
    }
    for (int i = 1; i <= n; i++)
    {
        int x;
        cin >> x;
        b[i] = b[i - 1] + x;
    }
    for (int i = 1; i <= n; i++)
    {
        int x;
        cin >> x;
        c[i] = c[i - 1] + x;
    } // 以上全部为求前缀和
    int ans = -INF, X = a[1] - b[1] // 当前 ax - bx 的最大值;
    for (int y = 2; y < n; y++)
    {
        ans = max(ans, b[y] - c[y] + X); // 保留最优解
        X = max(X, a[y] - b[y]); // 维护最大值
    }
    cout << ans + c[n]; // 别忘了 cn
    return 0;
}

E - 重型水桶

时间限制：3 秒

内存限制：1024 MiB

分值：475 分

题目描述

有 NNN 个人和 NNN 个水桶，人和水桶的编号均为 1,2,...,N1,2,\dots,N1,2,...,N。

初始状态下，第 iii 个人只持有第 iii 号水桶，且所有水桶都是空的。

接下来，重复执行以下操作 10910^9109 次：

对所有 i=1,2,...,Ni=1,2,\dots,Ni=1,2,...,N 同时执行：第 iii 个人向自己手中的每一个 水桶中加入 iii 单位的水，然后将这些水桶全部交给第 AiA_iAi 号人。水桶的容量没有上限。

有 QQQ 次询问，对于第 iii 次询问，请你回答：

在第 TiT_iTi 次操作完成后 ，第 BiB_iBi 号水桶中的水量是多少。

数据范围

2≤N≤2×1052 \le N \le 2 \times 10^52≤N≤2×105

1≤Q≤2×1051 \le Q \le 2 \times 10^51≤Q≤2×105

1≤Ai≤N1 \le A_i \le N1≤Ai≤N

1≤Ti≤1091 \le T_i \le 10^91≤Ti≤109

1≤Bi≤N1 \le B_i \le N1≤Bi≤N

所有输入均为整数。

解题思路

这是一道倍增思想的经典题目，我们可以建立两个二维数组 pos 和 v 来解决问题：

pos[i][j]：表示编号为 i 的水桶，从初始状态开始经历 2j2^j2j 轮操作（传递+加水）后，最终在谁的手中。
v[i][j]：表示编号为 i 的水桶，从初始状态开始经历 2j2^j2j 轮操作后，总共增加的水量。

基于倍增思想的递推性质，我们可以得到以下两个核心转移公式：

pos[i][j] = pos[pos[i][j - 1]][j - 1]
v[i][j] = v[i][j - 1] + v[pos[i][j - 1]][j - 1]

下面对这两个公式进行详细解释：

对于位置转移公式 pos[i][j] = pos[pos[i][j - 1]][j - 1]：我们先假设已知「编号为 i 的水桶经过 2j−12^{j-1}2j−1 轮操作后，会到达 pos[i][j-1] 这个人的手中」。而根据 pos 数组的定义，pos[pos[i][j-1]][j-1] 表示「编号为 pos[i][j-1] 的水桶经过 2j−12^{j-1}2j−1 轮操作后到达的人的编号」。由于所有水桶的传递规则完全由接收人数组 A 决定，与水桶编号无关，因此编号为 i 的水桶到达 pos[i][j-1] 手中后，后续的传递路径会和「编号为 pos[i][j-1] 的水桶的初始传递路径」完全一致。也就是说，编号为 i 的水桶在完成前 2j−12^{j-1}2j−1 轮传递后，再经过 2j−12^{j-1}2j−1 轮传递，最终会到达 pos[pos[i][j-1]][j-1] 手中，这恰好就是 2j2^j2j 轮传递后的最终位置，即 pos[i][j]。
对于水量累加公式 v[i][j] = v[i][j - 1] + v[pos[i][j - 1]][j - 1]：水桶的加水规则仅由「持有它的人」决定（第 k 个人持有水桶时，会给水桶加 k 单位的水），与水桶的编号、操作的起始轮次无关。编号为 i 的水桶经过 2j2^j2j 轮操作的总水量，可拆分为两部分： - 前 2j−12^{j-1}2j−1 轮操作增加的水量，即 v[i][j-1]； - 后 2j−12^{j-1}2j−1 轮操作增加的水量：此时水桶已经到达 pos[i][j-1] 手中，后续 2j−12^{j-1}2j−1 轮的加水过程，与「编号为 pos[i][j-1] 的水桶初始状态下经过 2j−12^{j-1}2j−1 轮操作的加水过程」完全一致，对应的水量就是 v[pos[i][j-1]][j-1]。两者相加即为 v[i][j]，也就是编号为 i 的水桶经过 2j2^j2j 轮操作的总增水量。

最后我们将回合数拆分成二进制进行求解，时间复杂度根据代码简单计算即可。

代码

cpp 复制代码

#include <bits/stdc++.h>
#define int long long

using namespace std;

const int maxn = 2e5 + 5, maxq = 2e5 + 5;
int n, q, pos[maxn][35], v[maxn][35];

signed main()
{
    cin >> n >> q;
    for (int i = 1; i <= n; i++)
    {
        int a;
        cin >> a;
        pos[i][0] = a;
        v[i][0] = i;
    }
    for (int i = 1; i <= 30; i++)
        for (int j = 1; j <= n; j++) // 转移
        {
            pos[j][i] = pos[pos[j][i - 1]][i - 1];
            v[j][i] = v[j][i - 1] + v[pos[j][i - 1]][i - 1];
        }
    for (int i = 1; i <= q; i++)
    {
        int b, t;
        cin >> t >> b;
        int cur = b, ans = 0;
        for (int j = 30; j >= 0; j--) // 将 t 变成二进制，如果发现有 1 存在，那么我们就传递对应的回合
        {
            if (t & (1 << j))
                ans += v[cur][j], cur = pos[cur][j]; // 传递 2^j 回合
        }
        cout << ans << '\n';
    }
    return 0;
}

F - 最小未出现值的和

时间限制：2 秒

内存限制：1024 MiB

分值：525 分

题目描述

给定一棵有 NNN 个顶点的树 TTT，顶点编号为 000 到 N−1N-1N−1。

第 iii 条边（1≤i≤N−11 \le i \le N-11≤i≤N−1）双向连接顶点 uiu_iui 和 viv_ivi。（注：顶点采用 0 下标编号，边采用 1 下标编号）

对于满足 0≤i,j<N0 \le i,j < N0≤i,j<N 的整数对 (i,j)(i,j)(i,j)，定义函数 f(i,j)f(i,j)f(i,j) 如下：

在树 TTT 中，从顶点 iii 到顶点 jjj 的路径不包含 的所有顶点中，编号最小的那个顶点的编号，即为 f(i,j)f(i,j)f(i,j)。特别地，如果从顶点 iii 到顶点 jjj 的路径包含了从 000 到 N−1N-1N−1 的所有顶点（即包含全部顶点），则令 f(i,j)=Nf(i,j) = Nf(i,j)=N。（注：树中从顶点 iii 到顶点 jjj 的路径包含顶点 iii 和顶点 jjj 本身）

请你求出下式的值：

∑0≤i≤j<Nf(i,j)\sum_{0 \le i \le j < N} f(i,j)0≤i≤j<N∑f(i,j)

数据范围

2≤N≤2×1052 \le N \le 2 \times 10^52≤N≤2×105

0≤ui<vi<N0 \le u_i < v_i < N0≤ui<vi<N

输入给定的图是一棵合法的树，所有输入均为整数

解题思路

我们先来明确一个核心问题：

路径的贡献何时为 iii？显然，只有当一条路径满足两个条件 时，它对答案的贡献才会是 iii：

路径上包含了 0,1,...,i−10, 1, ..., i-10,1,...,i−1 所有顶点（保证路径补集的 mex 至少为 iii）；
路径上不包含顶点 iii（保证路径补集的 mex 不超过 iii，二者结合即 mex 恰好为 iii）。

结合树的性质，0,1,...,i−10, 1, ..., i-10,1,...,i−1 这些顶点相互连接形成的结构必然是一条链（连通且无环的树结构，且按顺序递增的顶点集合在树中只能构成链）。因此，当我们要往这个链中加入新的顶点 iii 时，无需考虑链的中间节点，只需聚焦这条链的两个端点即可（这两个端点决定了链的边界和后续路径的范围）。

接下来我们介绍具体的计算方法：

首先以顶点 000 为根节点构建树的邻接表，并通过深度优先搜索（DFS）预处理出每个顶点的子树大小；
针对上述链的两个端点，分别计算其有效子树大小：其中靠近顶点 iii的那个端点，需要将其原始子树大小** 减去顶点 iii 的子树大小** （这是因为顶点 iii 不在合法路径上，需要排除其对应的子树范围，得到仅包含 0,1,...,i−10, 1, ..., i-10,1,...,i−1 的有效子树规模）；
最后将两个端点的有效子树大小相乘，得到的结果就是当前满足「贡献为 iii」的路径数量（对应示意图中的红色部分，即所有合法的 (i,j)(i,j)(i,j) 对数量）。

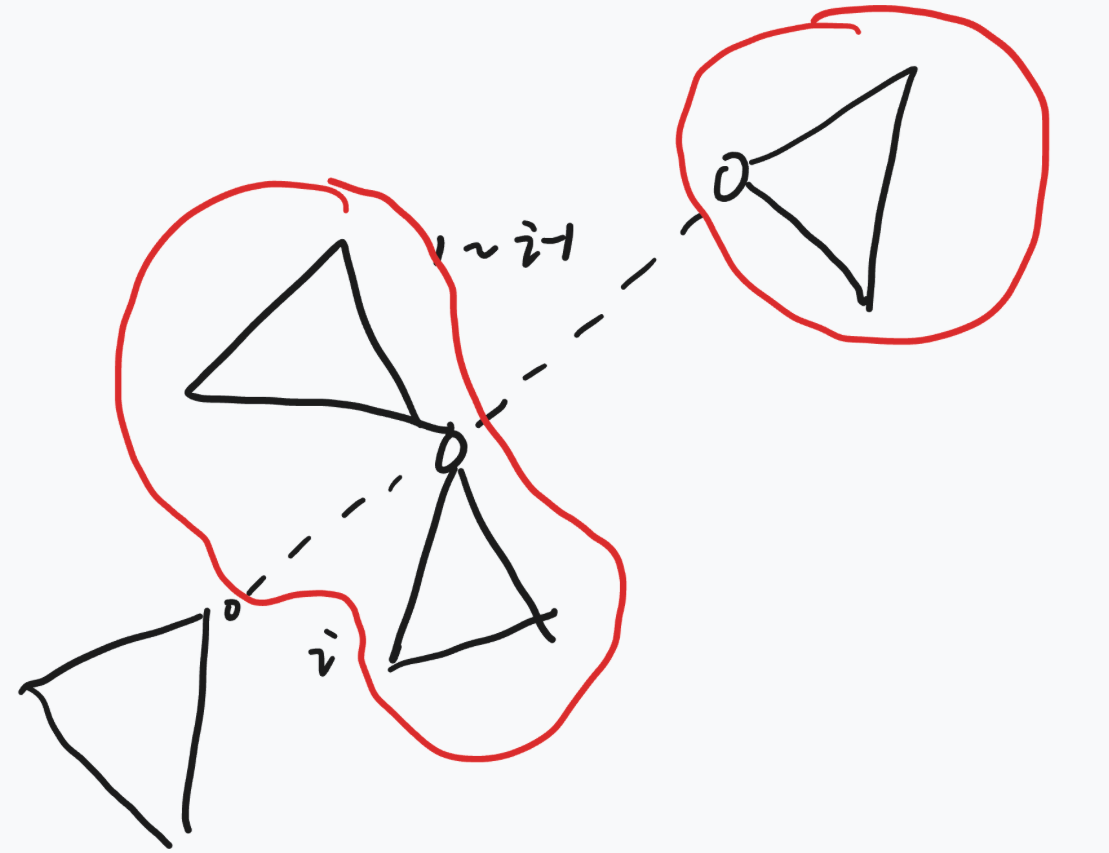
最后我们把 i 维护进两个端点即可。

不过要注意当 i 等于 1 的时候，是没有两个端点的，我们要特殊处理，具体看代码。

代码

cpp 复制代码

#include <bits/stdc++.h>
#define int long long

using namespace std;

const int maxn = 2e5 + 5;
vector<int> e[maxn];
int n, fa[maxn], sz[maxn], vis[maxn];
int ans = 1;

void dfs(int x) // dfs 求解每个节点的父亲和子树大小，根节点为 0
{
    sz[x] = 1;
    for (int i = 0; i < e[x].size(); i++)
    {
        int v = e[x][i];
        if (v == fa[x])
            continue;
        fa[v] = x;
        dfs(v);
        sz[x] += sz[v];
    }
    return;
}

int up(int x) // 向上寻找端点，返回这条路径上最靠近端点的节点
{
    vis[x] = 1;
    if (vis[fa[x]] > 0) 
        return x;
    return up(fa[x]);
}

signed main()
{
    cin >> n;
    fa[0] = -1;
    for (int i = 1; i < n; i++)
    {
        int u, v;
        cin >> u >> v;
        e[u].push_back(v);
        e[v].push_back(u);
    }
    dfs(0);
    vis[0] = 2; // vis = 2 表示为端点，vis = 1 表示是在链上，但不是端点的节点，vis = 0 表示不再链上的点
    int x = up(1); // 处理 i = 1 的特殊情况
    int sum = 1;
    for (int i = 0; i < e[0].size(); i++) // 枚举 0 的所有子树，一个子树的点可以和其他子树的点，形成一条符合条件的路径
    {
        int v = e[0][i];
        if (v == x) // 如果是包含 1 的子树，那么我们要把 1 的子树排除掉
            ans += sum * (sz[x] - sz[1]), sum += sz[x] - sz[1];
        else
            ans += sum * sz[v], sum += sz[v];
    }
    vis[1] = 2; // 记为端点
    sz[0] -= sz[x]; 
    int endp[2] = {0, 1}; // endp 保存两个端点是什么
    for (int i = 2; i < n; i++)
    {
        if (vis[i]) // 已经在链表上了就跳过
            continue;
        x = up(i);
        if (vis[fa[x]] == 1) // 说明分叉了，i 不可能和 0 ～ i-1 在一条链上
        {
            ans += sz[endp[0]] * sz[endp[1]] * i; // 把这一次答案计入后直接输出结果
            cout << ans;
            return 0;
        }
        int multi_ans = 1;
        for (int j = 0; j <= 1; j++)
            if (endp[j] == fa[x]) // 靠近 i 的节点，因为端点可能是 0，所以将自己的子树大小减少 sz[i]，然后把 i 维护到端点里
                multi_ans *= sz[endp[j]] - sz[i], sz[endp[j]] -= sz[x], vis[i] = 2, vis[endp[j]] = 1, endp[j] = i;
            else
                multi_ans *= sz[endp[j]];
        ans += multi_ans * i;
    }
    cout << ans + n; // 如果 0 ～ n-1 可以形成一条链，那么这条路径的贡献为 n
    return 0;
}

G - 最小值的和

时间限制：2 秒

内存限制：1024 MiB

分值：575 分

题目描述

给定整数 NNN、MMM、KKK，以及一个长度为 NNN 的整数序列 A=(A0,A1,...,AN−1)A=(A_0, A_1, \dots, A_{N-1})A=(A0,A1,...,AN−1) 和一个长度为 MMM 的整数序列 B=(B0,B1,...,BM−1)B=(B_0, B_1, \dots, B_{M-1})B=(B0,B1,...,BM−1)。（注：序列的下标均从 0 开始）

请你计算以下求和式的值，并对 998244353998244353998244353 取模：

∑i=0K−1min⁡(Ai mod N, Bi mod M)\sum_{i=0}^{K-1} \min\left(A_{i \bmod N},\ B_{i \bmod M}\right)i=0∑K−1min(AimodN, BimodM)

数据范围

1≤N,M≤2×1051 ≤ N, M ≤ 2 × 10^51≤N,M≤2×105

1≤K≤10181 ≤ K ≤ 10^181≤K≤1018

1≤Ai,Bi≤1091 ≤ A_i, B_i ≤ 10^91≤Ai,Bi≤109

所有输入均为整数

解题思路

这道题的核心难点在于 KKK 极大（可达 101810^{18}1018），且直接计算 NNN 和 MMM 的最小公倍数可能出现溢出（当二者互质时公倍数为 N×MN \times MN×M，最大可达 4×10104 \times 10^{10}4×1010，无法直接枚举和存储）。

首先，当 gcd⁡(N,M)\gcd(N, M)gcd(N,M) 不为 1 时，我们可以对 AAA 和 BBB 两个数组采用分组处理的思路来简化问题。令 g=gcd⁡(N,M)g = \gcd(N, M)g=gcd(N,M)，通过分析可以发现，若 AiA_iAi 和 BjB_jBj 会在某个下标 ttt 处形成 min⁡(At mod N,Bt mod M)\min(A_{t \bmod N}, B_{t \bmod M})min(AtmodN,BtmodM) 的配对并进行大小比较，那么必然满足 i%g==j%gi \% g == j \% gi%g==j%g。基于这个规律，我们可以将 AAA 和 BBB 中的所有元素按照对 ggg 取模的结果进行分组，每一组对应一个余数 rrr（0≤r<g0 \le r < g0≤r<g），这样就将原问题拆解为了 ggg 个相互独立的子问题，而每个子问题中对应的序列长度之比的最大公约数为 1，即实现了 gcd⁡(N′,M′)=1\gcd(N', M') = 1gcd(N′,M′)=1 的简化效果，为后续计算扫清了障碍。

接下来我们聚焦于简化后的子问题（gcd⁡(N,M)=1\gcd(N, M) = 1gcd(N,M)=1），探讨如何高效计算结果。其实在计算最小值之和时，我们无需关注每一对配对的具体最小值，只需聚焦于每个数字作为最小值时的贡献即可。具体来说，计算贡献的核心逻辑是：维护当前比目标数字大的所有数字的个数，用这个数字本身乘以对应的个数，得到的结果就是该数字对最终答案的总贡献，这种方式避开了逐一对比较的低效操作。

假设我们现在要计算 AkA_kAk 对答案的贡献，首先明确 AkA_kAk 会参与 ttt 轮大小比较（即与 ttt 个 BBB 数组元素配对）。如果 t=mt = mt=m，那么 AkA_kAk 会与 BBB 数组中的所有元素进行比较，此时由于 gcd⁡(N,M)=1\gcd(N, M) = 1gcd(N,M)=1，结合扩展欧几里得定理的结论，我们只需直接维护比 AkA_kAk 大的 BBB 数组元素个数，即可快速算出 AkA_kAk 的总贡献。但如果 t%m≠0t \% m \neq 0t%m=0，说明 AkA_kAk 并未与 BBB 数组所有元素配对，此时就需要单独考虑在剩余的回合中，AkA_kAk 所能产生的贡献。

进一步分析 AkA_kAk 对应的 BBB 数组元素下标，我们可以发现其呈现出明显的规律，对应的 BBB 数组元素依次为 Bk%mB_{k \% m}Bk%m、Bk%m+1×n%mB_{k \% m + 1 \times n \%m}Bk%m+1×n%m、Bk%m+2×n%mB_{k \% m + 2 \times n \%m}Bk%m+2×n%m、Bk%m+3×n%mB_{k \% m + 3 \times n \%m}Bk%m+3×n%m...... 由于我们已经通过扩展欧几里得定理得到了 nnn 在模 mmm 下的逆元，因此可以在模 mmm 的前提下，将这些 BBB 数组的下标全部除以 nnn（本质上是乘以 nnn 的逆元）。经过这样的转换后，原本分散的下标会变成连续的序列，即依次为 Bk/n%mB_{k /n \% m}Bk/n%m、Bk/n%m+1%mB_{k/n \% m + 1 \%m}Bk/n%m+1%m、Bk/n%m+2%mB_{k / n \% m + 2 \%m}Bk/n%m+2%m、Bk/n%m+3%mB_{k / n \% m + 3\%m}Bk/n%m+3%m...... 下标连续的特性恰好可以被树状数组高效处理，我们可以通过树状数组维护元素的处理状态和区间计数，快速查询到合法的元素个数，进而顺利算出 AkA_kAk 在剩余回合中的贡献，最终完成整个问题的求解。

代码

cpp 复制代码

#include <bits/stdc++.h>
#define int long long // 懒人开long long
using namespace std;

const int MOD = 998244353;

struct tree // 树状数组
{
    vector<int> t;
    int n;

    void init(int _n)
    {
        n = _n;
        t.assign(n + 2, 0);
    }

    void update(int pos, int val)
    {
        pos++;
        for (; pos <= n; pos += pos & -pos)
            t[pos] = (t[pos] + val) % MOD;
    }

    int query(int pos)
    {
        pos++;
        int s = 0;
        for (; pos > 0; pos -= pos & -pos)
            s = (s + t[pos]) % MOD;
        return s;
    }
};

int gcd(int a, int b) // 最大公因数
{
    while (b)
    {
        int tmp = b;
        b = a % b;
        a = tmp;
    }
    return a;
}

int solve_sub(int n, int m, int K, vector<int> &A, vector<int> &B) // 参数含义与 solve 相同，此时 gcd(n, m) 相同
{
    int ret = 0;
    vector<pair<int, int>> a; // 把所有的元素按照从小到达的顺序进行排序，维护位置的时候，我们让 B 去后面以此进行区分
    for (int i = 0; i < n; i++)
        a.push_back({A[i], i});
    for (int i = 0; i < m; i++)
        a.push_back({B[i], n + i});
    sort(a.begin(), a.end());
    int N = n, M = m; // 先计算每一个周期（n * m 轮游戏）的结果是多少，再去计算剩下的部分
  // 此时 N 和 M 表示比第 i 个元素大的 A 和 B 的数量
    for (int i = 0; i < a.size(); i++)
    {
        int w = a[i].first, idx = a[i].second;
        if (idx < n) // A 元素
        {
            ret += w * M % MOD, ret %= MOD; // 记得取模
            N--; // 后面的都比它大，直接去掉
        }
        else // 同理
        { 
            ret += w * N % MOD, ret %= MOD;
            M--;
        }
    }
    ret *= K / (n * m) % MOD, ret %= MOD; // 乘以周期数
    K %= n * m; // 看看还剩下多少轮
    tree X, Y;
    X.init(2 * n + 100); // 和环形 dp 一样，为了防止右边界出界，我们直接 double 一下
    Y.init(2 * m + 100);
    int nt, mt;
    for (int i = 1; i < m; i++) // 在模 m 的前提下，计算 n 的逆元，也可以用 exgcd，这里我偷懒了
        if (i * n % m == 1)
            nt = i;
    for (int j = 1; j < n; j++) // 在模 n 的前提下，计算 m 的逆元
        if (j * m % n == 1)
            mt = j;
    for (int i = 0; i < 2 * n; i++) // 两个数组分别维护有效的（更大）的 A 元素和 B 元素的数量
        X.update(i, 1);
    for (int j = 0; j < 2 * m; j++)
        Y.update(j, 1);
    for (int i = 0; i < a.size(); i++)
    {
        int w = a[i].first, idx = a[i].second;
        if (idx < n)
        {
            int t = K / n + (idx < K % n); // 还要比较多少轮
            int l = idx * nt % m; // 找左端点
            int len = Y.query(l + t - 1) - Y.query(l - 1); // 计算在范围内，还有多少个比 a[i] 大的 
            ret += w * len % MOD, ret %= MOD;
            X.update(idx * mt % n, -1); // 后面枚举的更大，现在这个元素没用了
            X.update(idx * mt % n + n, -1);
        }
        else
        { // 同理，直接 copy 过来即可
            idx -= n;
            int t = K / m + (idx < K % m);
            int l = idx * mt % n;
            int len = X.query(l + t - 1) - X.query(l - 1);
            ret += w * len % MOD, ret %= MOD;
            Y.update(idx * nt % m, -1);
            Y.update(idx * nt % m + m, -1);
        }
    }
    return ret;
}

int solve(int N, int M, int K, vector<int> &A, vector<int> &B) // A 的长度，B 的长度，要进行多少轮游戏，A 和 B 的指针 
{
    int g = gcd(N, M); // 此时的 g 不一定为 1
    int n = N / g, m = M / g;
    int ret = 0;
    for (int r = 0; r < g; ++r)
    {
        vector<int> As, Bs;
        for (int i = 0;; ++i)
        {
            int pos = r + i * g;
            if (pos >= N)
                break;
            As.push_back(A[pos]);
        }
        for (int i = 0;; ++i)
        {
            int pos = r + i * g;
            if (pos >= M)
                break;
            Bs.push_back(B[pos]);
        }
        int Kr = (K > r) ? ((K - 1 - r) / g + 1) : 0;
        ret = (ret + solve_sub(n, m, Kr, As, Bs)) % MOD; // 根据对 g 取模的结果进行分组，用指针传递进下一个函数里面
    }
    return ret;
}

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    int N, M, K;
    cin >> N >> M >> K;
    vector<int> A(N), B(M);
    for (int i = 0; i < N; ++i)
        cin >> A[i];
    for (int i = 0; i < M; ++i)
        cin >> B[i];
    cout << solve(N, M, K, A, B) << endl;
    return 0;
}