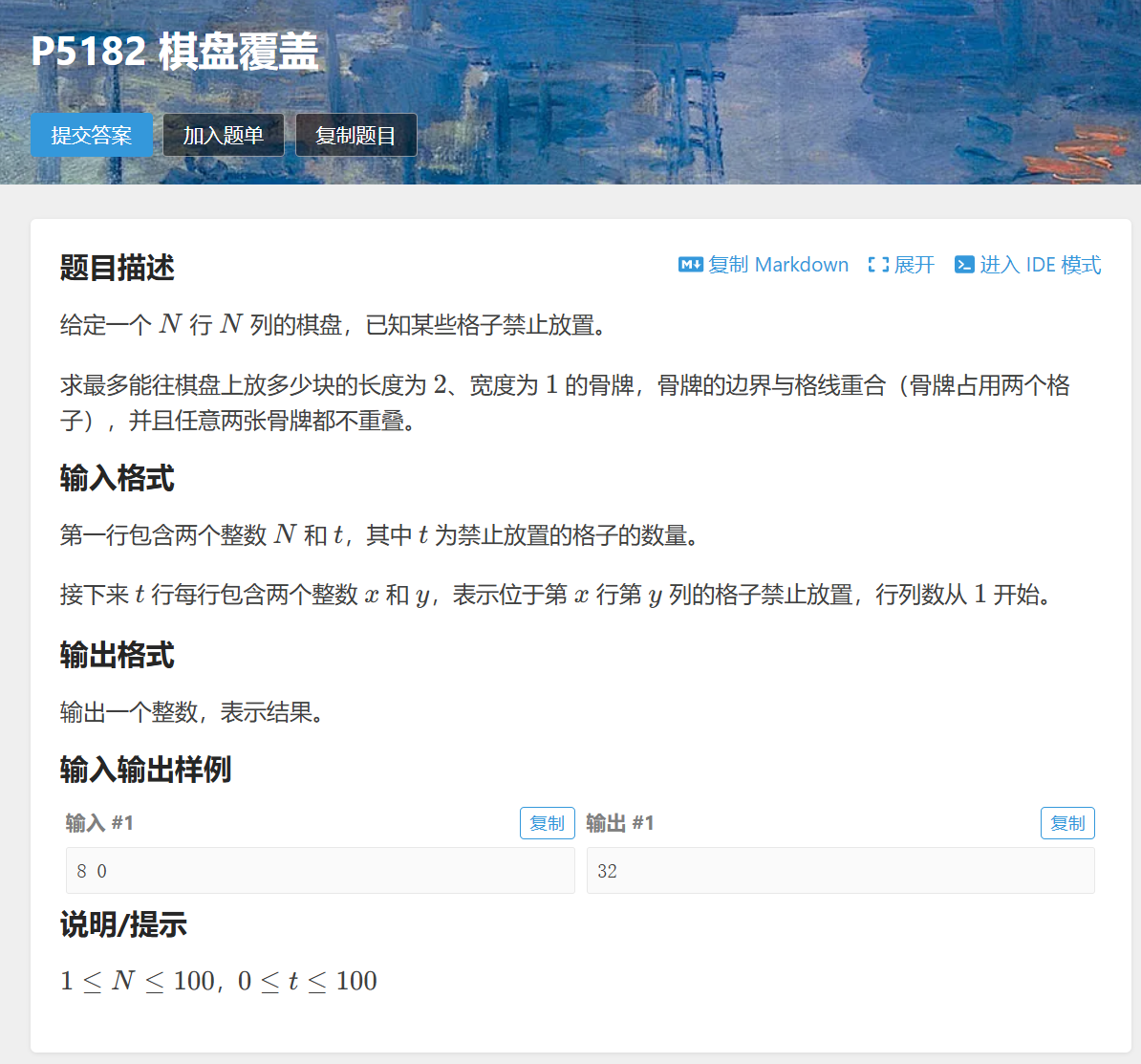
 【题目含义】
【题目含义】
- 一个NxN 的棋盘(N<100)
- 某些格子是坏的(不能放骨牌)
- 要用1×2的骨牌覆盖所有非坏的格子
- 骨牌不能重叠,不能覆盖坏格子
- 问:最多能放多少块骨牌
【思考】
一块骨牌,覆盖的格子有啥特点?
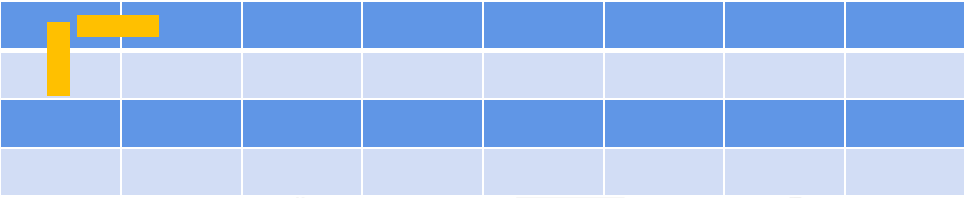
对于棋盘、方格类的情况,我们可以从每个格子的坐标考虑,看是否能有发现。
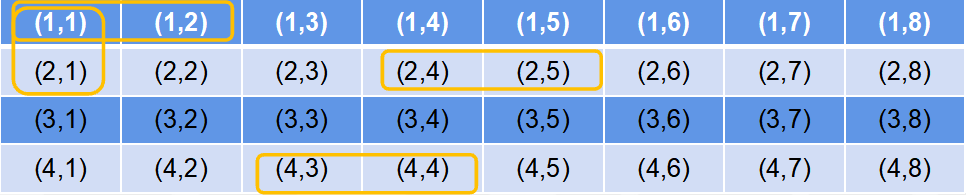
→ 一块骨牌覆盖的格子,是相邻的且横纵坐标之和一奇一偶。

关键观察
- 棋盘可以黑白染色
- 每个骨牌覆盖一黑一白两个相邻格子
- 坏格子相当于删去对应的顶点
标题问题:最多放多少条骨牌
→把多少个不重复的可用点连接(一黑一白)
考虑是二分图的最大匹配问题
【建图】
- 把棋盘每个有效格子看作顶点
- 黑格子和白格子分别作为二分图的两个部分
- 如果两个格子相邻(上下左右)且都是好格子,则在它们之间连一条边
- 每个骨牌对应一条匹配边

求解过程整理
- 每个骨牌覆盖相邻的一黑一白 → 匹配边
- 骨牌不重叠 → 匹配中每个顶点只被一条边使用
- 最大化骨牌数量 → 最大化匹配边数 匈牙利算法
注意点
1.将二维坐标 (i,j) 映射为节点编号:
常用方法:id = (i-1) * N + j,但需要区分黑白
2.国际象棋盘:(i+j)%2=0 为 黑格或者 (i+j)%2=1 为白格
两种方式都可以,只要相邻格子颜色不同
cpp
#include<bits/stdc++.h>
using namespace std;
const int N=10009;
int a[109][109];
int match[N];
bool vis[N];
vector<int>g[N];
int n,t;
bool dfs(int x)
{
for(int i:g[x])
{
if(!vis[i])
{
vis[i]=true;
if(match[i]==-1 || dfs(match[i]))
{
match[i]=x;
return true;
}
}
}
return false;
}
int id(int i,int j)
{
return (i-1)*n+j;
}
bool black(int i,int j)
{
return (i+j)%2==0;
}
int main()
{
cin>>n>>t;
while(t--)
{
int x,y;
cin>>x>>y;
a[x][y]=1;
}
//jiantu
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if(a[i][j]) continue;
if(!black(i,j)) continue;
int id1=id(i,j);
//下
if( i!=n && !a[i+1][j] )
{
int id2=id(i+1,j);
g[id1].push_back(id2);
}
//右
if( j!=n && !a[i][j+1] )
{
int id2=id(i,j+1);
g[id1].push_back(id2);
}
//上
if(i>=1 && !a[i-1][j])
{
int id2=id(i-1,j);
g[id1].push_back(id2);
}
//左
if(j >=1 && !a[i][j-1])
{
int id2=id(i,j-1);
g[id1].push_back(id2);
}
}
}
//匈牙利
memset(match,-1,sizeof match);
int ans=0;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if(a[i][j]) continue;
if(!black(i,j)) continue;
int id1=id(i,j);
memset(vis,0,sizeof vis);
if(dfs(id1))
ans++;
}
}
cout<<ans;
return 0;
} 我的锅有哪些
1.数组开小了
cpp
const int N=109;
int a[109][109];
int match[N];
bool vis[N];
vector<int>g[N];刚开始,我的数组开109,但是
数组 g[N], match[N], vis[N],这些是存储图节点坐标的节点标号,
而节点编号范围:id = (i-1)*n + j
当 n=100 时,最大编号:(100-1)*100 + 100 = 9900 + 100 = 10000
所以需要 N > 10000,这里取 10009
每次开数组时,要问问这个数组下标存储是是啥!!!
2. 建图只建了向右、向下的边,但实际向上、向左都要建。
cpp
int id1=id(i,j);
//下
if( i!=n && !a[i+1][j] )
{
int id2=id(i+1,j);
g[id1].push_back(id2);
}
//右
if( j!=n && !a[i][j+1] )
{
int id2=id(i,j+1);
g[id1].push_back(id2);
}四个方向又要建
cpp
// 建图:黑格 -> 相邻的白格(四个方向)
// 使用方向数组更简洁
int dx[4] = {-1, 1, 0, 0}; // 上下左右
int dy[4] = {0, 0, -1, 1};
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
if(a[i][j]) continue;
if(!black(i, j)) continue;
int u = id(i, j);
for(int k = 0; k < 4; k++) {
int x = i + dx[k];
int y = j + dy[k];
// 检查边界
if(x < 1 || x > n || y < 1 || y > n) continue;
if(a[x][y]) continue; // 邻居是坏格子
int v = id(x, y);
g[u].push_back(v);
}
}
}3.边界问题,导致RE
cpp
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if(a[i][j]) continue;
if(!black(i,j)) continue;
int id1=id(i,j);
//下
if(!a[i+1][j] && i!=n )
{
int id2=id(i+1,j);
g[id1].push_back(id2);
}
//右
if(!a[i][j+1] && j!=n)
{
int id2=id(i,j+1);
g[id1].push_back(id2);
}
......这个写法,RE这么多
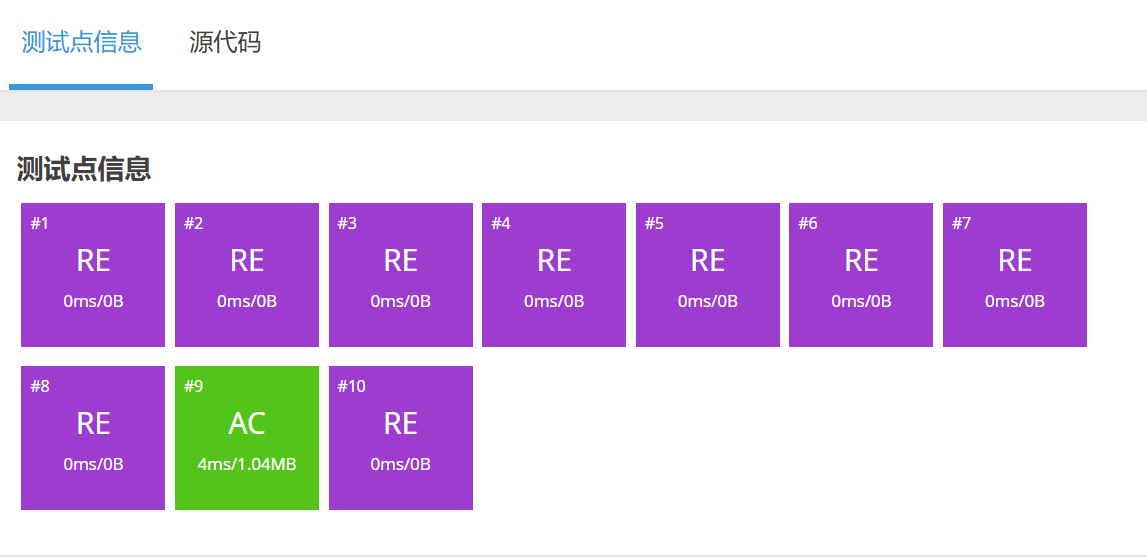
问题在于
cpp
if(!a[i+1][j] && i!=n )//要先判出界 再判断 是否是废格
......
if(!a[i][j+1] && j!=n)//要先判出界 再判断 是否是废格当 i=n 时:
i!=n 为 false
但由于短路求值,C++会先计算 !a[i+1][j]
此时 i+1 = n+1,a[n+1][j] 数组越界!
即使 i!=n 为 false,也已经访问了非法内存
逻辑与(&&)的短路求值规则:
对于 A && B,如果 A 为 false,B 不会被计算
所以要先放边界检查,再放数组访问
【总结】
- 边界检查要放在数组访问之前
- 对于多维数组,要特别注意下标范围
- 考虑使用方向数组来统一处理边界
- 记住:先检查,再访问!
匈牙利算法中每一轮没恢复vis的值
cpp
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if(a[i][j]) continue;
if(!black(i,j)) continue;
int id1=id(i,j);
//memset(vis,0,sizeof vis);这里没恢复成0
if(dfs(id1))
ans++;
}
}为什么每次都要清零?
匈牙利算法寻找增广路:
对每个黑格(左部节点)尝试匹配
每次尝试都需要寻找一条增广路
vis 数组标记当前这次尝试中访问过的白格(右部节点)
举个例子
图:
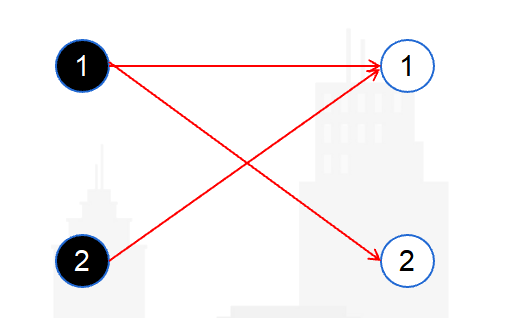
-
第一次尝试(黑格1匹配白格1):
vis[白格1] = true
匹配成功:match[白格1] = 黑格1
-
第二次尝试(黑格2匹配):
需要重新开始找增广路
如果不清零,vis[白格1] 还是 true
算法会跳过白格1,但其实应该尝试让白格1换匹配,可能错失更好的匹配方案
-
清零的作用
每次 dfs(u) 前清零 vis:
表示"重新开始一次增广路搜索"
允许重新考虑之前匹配过的白格
让这些白格有机会改变匹配对
4. 二维坐标转一维标号的问题
cpp
int id(int i,int j)
{
return i*n+j;
} 来看一下,id = i*n + j的编号效果
cpp
(1,1): 1*3+1 = 4
(1,2): 1*3+2 = 5
(1,3): 1*3+3 = 6
(2,1): 2*3+1 = 7
(2,2): 2*3+2 = 8
(2,3): 2*3+3 = 9
(3,1): 3*3+1 = 10
(3,2): 3*3+2 = 11
(3,3): 3*3+3 = 12来看一下,id = (i-1)*n + j的编号效果
cpp
(1,1): (1-1)*3+1 = 0*3+1 = 1
(1,2): (1-1)*3+2 = 0*3+2 = 2
(1,3): (1-1)*3+3 = 0*3+3 = 3
(2,1): (2-1)*3+1 = 1*3+1 = 4
(2,2): (2-1)*3+2 = 1*3+2 = 5
(2,3): (2-1)*3+3 = 1*3+3 = 6
(3,1): (3-1)*3+1 = 2*3+1 = 7
(3,2): (3-1)*3+2 = 2*3+2 = 8
(3,3): (3-1)*3+3 = 2*3+3 = 9综上
in+j:编号不连续,浪费空间,范围是 [n+1, n (n+1)]
(i-1)n+j:编号连续,节省空间,范围是 [1, n n]
** 建议使用:公式直观:(行号-1)*列数 + 列号 **