目录
[示例 1:](#示例 1:)
[示例 2:](#示例 2:)
[示例 3:](#示例 3:)
[步骤 1:二分查找天数](#步骤 1:二分查找天数)
[步骤 2:对每个mid构建地图并判断是否连通(关键)](#步骤 2:对每个mid构建地图并判断是否连通(关键))
前言:
今年是2025年最后一天,祝大家身体健康,天天开心,学业有成,事业有成!
 新的一年新的成绩
新的一年新的成绩
这是一道是一个经典的"最后可行时间"类问题,可以使用二分查找 + BFS,希望可以给大家提供帮助!
题目:
给你一个下标从 1 开始的二进制矩阵,其中 0 表示陆地,1 表示水域。同时给你 row 和 col 分别表示矩阵中行和列的数目。
一开始在第 0 天,整个 矩阵都是 陆地 。但每一天都会有一块新陆地被 水 淹没变成水域。给你一个下标从 1 开始的二维数组 cells ,其中 cells[i] = [ri, ci] 表示在第 i 天,第 ri 行 ci 列(下标都是从 1 开始)的陆地会变成 水域 (也就是 0 变成 1 )。
你想知道从矩阵最 上面 一行走到最 下面 一行,且只经过陆地格子的 最后一天 是哪一天。你可以从最上面一行的 任意 格子出发,到达最下面一行的 任意 格子。你只能沿着 四个 基本方向移动(也就是上下左右)。
请返回只经过陆地格子能从最 上面 一行走到最 下面 一行的 最后一天 。
示例 1:
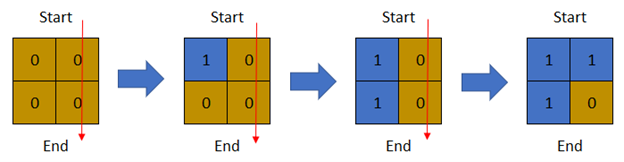
输入:row = 2, col = 2, cells = [[1,1],[2,1],[1,2],[2,2]]
输出:2
解释:上图描述了矩阵从第 0 天开始是如何变化的。
可以从最上面一行到最下面一行的最后一天是第 2 天。
示例 2:
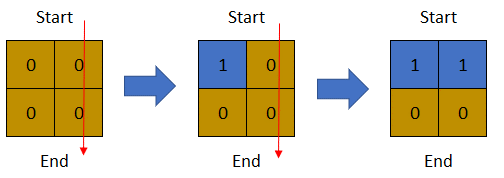
输入:row = 2, col = 2, cells = [[1,1],[1,2],[2,1],[2,2]]
输出:1
解释:上图描述了矩阵从第 0 天开始是如何变化的。
可以从最上面一行到最下面一行的最后一天是第 1 天。
示例 3:
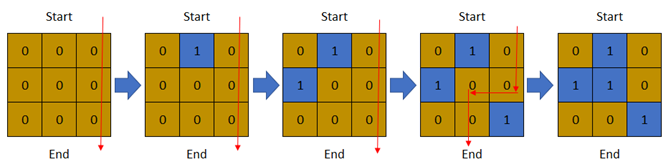
输入:row = 3, col = 3, cells = [[1,2],[2,1],[3,3],[2,2],[1,1],[1,3],[2,3],[3,2],[3,1]]
输出:3
解释:上图描述了矩阵从第 0 天开始是如何变化的。
可以从最上面一行到最下面一行的最后一天是第 3 天。
提示:
2 <= row, col <= 2 * 104
4 <= row * col <= 2 * 104
cells.length == row * col
1 <= ri <= row
1 <= ci <= col
cells 中的所有格子坐标都是 唯一 的。
题目分析:
读完题目,看完例题,我希望大家可以把握住一个点,一个非常核心的思想:
随着天数增加,陆地越来越少(水域越来越多),通行能力只会变差,不会变好
基于这个,我们就可以使用二分查找,因为
- 如果第
d天还能从上走到下 → 那么第1, 2, ..., d-1天也一定可以,因为那时水更少,陆地更多 - 如果第
d天不能走通 → 那么第d+1, d+2, ...天也一定不能,因为水只会更多
代码:
javaclass Solution { public int latestDayToCross(int row, int col, int[][] cells) { int left = 0; int right = cells.length; // 最多可能到第 n 天仍可通行 int result = 0; // 二分查找:找最大的可行天数 while (left <= right) { int mid = left + (right - left) / 2; if (canCross(row, col, cells, mid)) { result = mid; // 记录可行答案 left = mid + 1; // 尝试更晚的天数 } else { right = mid - 1; // 太晚了,往前找 } } return result; } // 判断在第 day 天(即前 day 个 cells 被淹没)是否还能从上走到下 private boolean canCross(int row, int col, int[][] cells, int day) { // 初始化网格:0 表示陆地,1 表示水域 int[][] grid = new int[row][col]; // 把前 day 天淹没的格子设为水域(注意:cells 是 1-indexed) for (int i = 0; i < day; i++) { int r = cells[i][0] - 1; // 转为 0-index int c = cells[i][1] - 1; grid[r][c] = 1; // 变成水 } // BFS:从第一行所有陆地出发 Queue<int[]> queue = new LinkedList<>(); boolean[][] visited = new boolean[row][col]; // 初始化:第一行的陆地入队 for (int j = 0; j < col; j++) { if (grid[0][j] == 0) { queue.offer(new int[]{0, j}); visited[0][j] = true; } } // 四个方向:上下左右 int[][] dirs = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}; while (!queue.isEmpty()) { int[] cur = queue.poll(); int x = cur[0], y = cur[1]; // 如果到达最后一行,成功! if (x == row - 1) { return true; } // 探索四个邻居 for (int[] dir : dirs) { int nx = x + dir[0]; int ny = y + dir[1]; // 边界检查 + 是否是陆地 + 是否未访问 if (nx >= 0 && nx < row && ny >= 0 && ny < col && grid[nx][ny] == 0 && !visited[nx][ny]) { visited[nx][ny] = true; queue.offer(new int[]{nx, ny}); } } } return false; // 无法到达底部 } }
代码分析:
步骤 1:二分查找天数
- 左边界 left = 0
- 右边界 right = cells.length(最多能走到第 n 天)
- 我们要找最大的 d,使得第 d 天还能走通。
- 为什么 right 是 cells.length?因为第 cells.length 天表示所有给定的格子都淹了,但可能仍能走通
javaint left = 0; int right = cells.length; // 最多可能到第 n 天仍可通行 int result = 0; // 二分查找:找最大的可行天数 while (left <= right) { int mid = left + (right - left) / 2; if (canCross(row, col, cells, mid)) { result = mid; // 记录可行答案 left = mid + 1; // 尝试更晚的天数 } else { right = mid - 1; // 太晚了,往前找 } } return result; }
步骤 2:对每个mid构建地图并判断是否连通(关键)
- 创建一个 row × col 的网格,初始全为陆地(0)。
- 把前 mid 天的 cells[0] 到 cells[mid-1] 标记为水域(1)。
- 然后从第一行所有陆地格子出发,做 BFS 或 DFS,看能否到达最后一行任意陆地格子。
- 如果能 → 说明第 mid 天可行,尝试更大的天数(left = mid + 1)
- 如果不能 → 说明太晚了,得往前找(right = mid - 1)
java// 判断在第 day 天(即前 day 个 cells 被淹没)是否还能从上走到下 private boolean canCross(int row, int col, int[][] cells, int day) { // 初始化网格:0 表示陆地,1 表示水域 int[][] grid = new int[row][col]; // 把前 day 天淹没的格子设为水域(注意:cells 是 1-indexed) for (int i = 0; i < day; i++) { int r = cells[i][0] - 1; // 转为 0-index int c = cells[i][1] - 1; grid[r][c] = 1; // 变成水 } // BFS:从第一行所有陆地出发 Queue<int[]> queue = new LinkedList<>(); boolean[][] visited = new boolean[row][col]; // 初始化:第一行的陆地入队 for (int j = 0; j < col; j++) { if (grid[0][j] == 0) { queue.offer(new int[]{0, j}); visited[0][j] = true; } } // 四个方向:上下左右 int[][] dirs = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}; while (!queue.isEmpty()) { int[] cur = queue.poll(); int x = cur[0], y = cur[1]; // 如果到达最后一行,成功! if (x == row - 1) { return true; } // 探索四个邻居 for (int[] dir : dirs) { int nx = x + dir[0]; int ny = y + dir[1]; // 边界检查 + 是否是陆地 + 是否未访问 if (nx >= 0 && nx < row && ny >= 0 && ny < col && grid[nx][ny] == 0 && !visited[nx][ny]) { visited[nx][ny] = true; queue.offer(new int[]{nx, ny}); } } } return false; // 无法到达底部 }
实现细节注意
-
下标转换:
- 题目说
cells[i] = [ri, ci]是 1-indexed - 代码中数组是 0-indexed → 要减 1:
(ri - 1, ci - 1)
- 题目说
-
BFS/DFS 起点:
- 把第一行所有
grid[0][j] == 0(陆地)加入队列 - 终止条件:走到任意
grid[row-1][j] == 0
- 把第一行所有
-
方向数组:
javaint[][] dirs = {{0,1},{0,-1},{1,0},{-1,0}};
结语:
这个题目也可以用并查集(Union-Find)逆序处理:从最后一天开始,逐步"恢复"陆地,直到上下连通。这也是常见解法。但我个人认为二分 + BFS 更直观,容易写对,推荐先掌握这个!
大家有兴趣可以搜一下解法!我这里就不赘述了!希望可以帮助到大家!我们2026年继续加油!