242-267 GHz双基地超外差雷达系统:面向精密太赫兹传感与成像的65nm CMOS实现
A. V. Muppala et al., "A 242-267 GHz Bistatic Superheterodyne Radar System for Precision Terahertz Sensing and Imaging in 65-nm CMOS," in IEEE Transactions on Microwave Theory and Techniques, vol. 73, no. 8, pp. 4999-5011, Aug. 2025, doi: 10.1109/TMTT.2025.3548036.
引言与研究背景
太赫兹(THz)频段雷达系统因其独特的物理特性,在高分辨率成像、无损检测和光谱分析等领域展现出巨大潜力。这篇发表于IEEE Transactions on Microwave Theory and Techniques的论文由密歇根大学Aditya Varma Muppala等人完成,报道了首个在CMOS工艺上实现的200 GHz以上相干成像雷达系统。该系统采用双基地超外差架构,在65nm CMOS工艺中实现了242-267 GHz的工作频段,峰值等效全向辐射功率(EIRP)达到-2 dBm,雷达带宽25 GHz,距离测量精度达到40 μm,速度测量精度达到80 μm/s。
现代雷达系统主要分为脉冲雷达、步进频率雷达和调频连续波(FMCW)雷达三大类。脉冲雷达广泛应用于远程目标探测和成像,如地面和卫星合成孔径雷达(SAR),其优势在于没有收发隔离问题且采样要求较低。步进频率雷达使用矢量网络分析仪(VNA)在频域测量散射数据,可通过傅里叶变换重建时域目标响应,虽能工作到太赫兹频段但积分时间较长。FMCW雷达发射线性调频chirp信号,回波与chirp信号的副本混频后产生中频(IF)信号,其频率直接映射到目标距离。此外,发送一系列chirp并联合处理可提供目标的多普勒速度。由于FMCW架构在采样前通过模拟混频器将数据"去斜"到基带,采样要求与射频信号带宽无关,允许工作频率远超数百吉赫兹,因此成为毫米波和太赫兹频段最广泛使用的架构。
然而,去斜接收FMCW雷达存在以下固有限制。首先是收发泄漏导致的低动态范围问题------发射功率必须受限以避免接收机饱和。其次是压控振荡器(VCO)的非线性和收发链路中的相位色散问题------chirp的任何非线性都会扭曲目标响应,这对三维相干图像重建尤为棘手。第三是相位噪声导致的低灵敏度和精度------相位噪声通常是锁相环(PLL)FMCW雷达实现更快、更线性chirp的限制因素。最后是中频频段的杂散干扰问题。这些问题在零差架构系统中更为严重,而文献中报道的绝大多数太赫兹雷达都采用零差架构。
针对这些挑战,文献中已提出多种解决方案。收发隔离可通过自适应自干扰消除或牺牲带宽来改善,共享收发天线系统在合理宽带宽上实现的最大隔离度为34 dB。更高隔离度(>50 dB)已通过空间功分器和准单基地系统实现,但该设置体积大,需要非常精确的对准且固有损耗为6 dB。关于chirp非线性,存在硬件和软件两种线性化方法:硬件方法估计VCO非线性并施加预失真电压波形生成线性频率chirp;后处理方法通常使用标准目标测量相位非线性并对采样IF数据施加色散数字滤波器。尽管这些方法在一定程度上有效,但FMCW雷达的相位校准比步进频率系统困难得多,因为IF数据在采样前已经去斜,而步进频率系统在每个频率点显式测量相位响应。
系统架构与信号模型
超外差锁相放大器架构
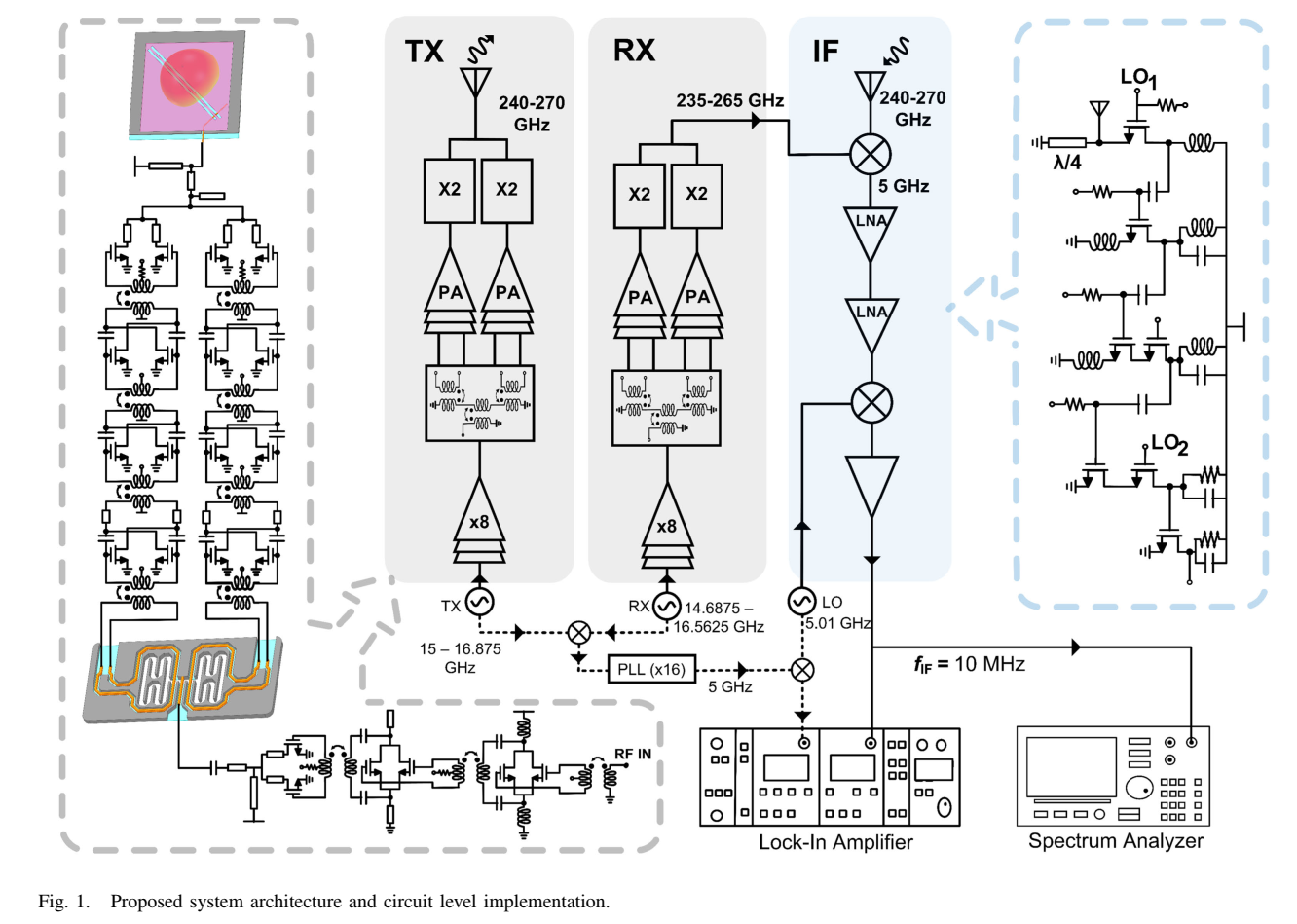
论文提出的系统架构如Fig. 1所示,由三个外部信号源产生连续波(CW)信号,分别构成发射(TX)、接收(RX)和本振(LO)信号。输入TX信号通过×16倍频器和放大器链,从场景反射后被RX接收。接收信号首先混频下变频到5 GHz中频,经放大后再次混频下变频到第二中频,送入锁相放大器(LIA)。同时,TX和RX信号的副本经混频后倍频到5 GHz,再下变频到第二中频。本质上存在两条信号路径:一条先进行频率上变频再混频下变频,另一条先混频下变频再进行频率上变频。因此两条信号路径是相干的,其中一条在太赫兹频段进行自由空间传播。LIA测量这两条信号路径之间的幅度和相位差,该相位差包含了目标在太赫兹频段的k空间散射信息,从而实现高分辨率图像重建。
该架构的核心优势在于:全部散射信息被编码到单一的用户定义CW信号上。步进TX和RX的频率会改变锁相信号的相位但不改变其频率,因此宽带雷达测量只需测量单一频率的中频信号。这正是该架构区别于脉冲、步进频率和FMCW雷达的关键特征。具体优势包括以下几个方面。
LIA的积分时间可设置得很大(如1000秒)以测量低于噪底30 dB的中频信号(这里的噪底是相对于1 Hz带宽而言,是频谱分析仪或VNA能达到的最低水平,因此LIA可比VNA灵敏得多),也可设置得很小(微秒级)使扫描时间与FMCW雷达的chirp持续时间相当。本质上,用户通过控制LIA的积分时间和灵敏度,完全掌控精度和延迟之间的权衡空间。中频信号频率由用户定义,意味着可将其置于PLL相位噪声"拐点"频率(即环路带宽)之外,相比FMCW系统改善了信噪比,因为FMCW系统中近距离目标的IF信号落在泄漏信号的1/f31/f^31/f3和1/f21/f^21/f2相位噪声谱内。微调IF频率的能力还允许用户避开IF频谱中的任何杂散。瞬时多普勒速度编码在锁相信号的频率上,可由频谱分析仪以很高精度直接测量,精度由频谱分析仪的分辨率带宽决定。由于相位在每个频率点直接测量,非线性可通过单个目标的响应和相位共轭轻松校正。超外差架构改善了噪声系数(NF),因为低噪声放大器(LNA)级现在工作在5 GHz,缓解了闪烁噪声退化。
因此,所提架构解决了FMCW雷达遇到的动态范围、灵敏度、非线性和干扰限制。可以将所提架构视为现有I/Q步进频率雷达的超外差扩展,具有更灵活的IF选择能力和修改LIA参数空间以适应不同应用的能力。虽然VNA提供类似的速度与灵敏度权衡,但LIA相比VNA有三个优势:首先,它可灵敏1000倍,因为VNA上的IF带宽不能任意缩小;其次,VNA受限于零差架构,输入和输出信号必须在相同频率,所提架构不受此限制;第三,LIA通常比VNA简单得多且便宜,使其可以集成到芯片上。
同样有必要提及所提架构的局限性。与FMCW雷达不同,位置和速度(即距离-多普勒图)不能同时测量,因为当目标运动时IF信号会改变,导致LIA失锁。对于高分辨率成像、无损检测和光谱学等应用,这一限制并不相关,因为目标通常是静态的。另一个主要限制是外部信号源和LIA的使用使系统体积较大。然而,如果LIA参数固定------比如针对特定应用------这些组件可以轻松集成到芯片上或PCB上。
收发隔离问题仍然存在。考虑到单芯片收发隔离在宽带宽上用现有技术无法超过40 dB,本文采用双基地(独立TX和RX芯片)配置以实现更高隔离。双基地配置不影响成像性能,这将在后面的成像部分展示。采用这种双基地配置并不从根本上解决单基地系统的隔离问题,而是针对近场成像这一具体应用绕过了它,因为在近场成像中TX和RX不需要共址。对于远场波束控制等其他应用,可采用准单基地系统。
雷达信号数学模型
假设TX和RX信号采用如下形式:
sT=ATcos(ωTt+ϕT),sR=ARcos(ωRt+ϕR)(1)s_T = A_T \cos(\omega_T t + \phi_T), \quad s_R = A_R \cos(\omega_R t + \phi_R) \tag{1}sT=ATcos(ωTt+ϕT),sR=ARcos(ωRt+ϕR)(1)
其中 fT=ωT/2πf_T = \omega_T/2\pifT=ωT/2π 从242 GHz步进到267 GHz,步进间隔0.1 GHz;fR=ωR/2πf_R = \omega_R/2\pifR=ωR/2π 从237 GHz步进到262 GHz,步进间隔同样为0.1 GHz。在给定步进点,TX和RX信号之间存在5 GHz的频差,且各自辐射CW信号。
TX信号辐射后从TX传播距离 rTr_TrT 到达目标,再从目标传播距离 rRr_RrR 到达RX。对于双基地系统,一般情况下 rT≠rRr_T \neq r_RrT=rR。接收信号与RX混频得到第一中频信号:
sIF1=AIF1cos((ωT−ωR)t+ϕT−ϕR+ωTc(rT+rR))(2)s_{\text{IF1}} = A_{\text{IF1}} \cos\left((\omega_T - \omega_R)t + \phi_T - \phi_R + \frac{\omega_T}{c}(r_T + r_R)\right) \tag{2}sIF1=AIF1cos((ωT−ωR)t+ϕT−ϕR+cωT(rT+rR))(2)
经LNA放大后,信号与频率为 ωT−ωR+ωIF\omega_T - \omega_R + \omega_{\text{IF}}ωT−ωR+ωIF 的第二中频信号混频,得到最终的10 MHz中频信号:
sIF=AIFcos(ωIFt−ϕIF−ωTc(rT+rR))(3)s_{\text{IF}} = A_{\text{IF}} \cos\left(\omega_{\text{IF}}t - \phi_{\text{IF}} - \frac{\omega_T}{c}(r_T + r_R)\right) \tag{3}sIF=AIFcos(ωIFt−ϕIF−cωT(rT+rR))(3)
其中 ϕIF\phi_{\text{IF}}ϕIF 是相对于参考10 MHz信号的任意常数相位因子(这里忽略了相位噪声,因为它在信号恢复中不重要)。LIA提取10 MHz中频相对于参考信号的幅度和相位,提取的相位形式为:
ϕLIA=∣ϕIF+ωTc(rT+rR)∣2π(4)\phi_{\text{LIA}} = \left|\phi_{\text{IF}} + \frac{\omega_T}{c}(r_T + r_R)\right|_{2\pi} \tag{4}ϕLIA= ϕIF+cωT(rT+rR) 2π(4)
其中 ∣⋅∣2π|\cdot|{2\pi}∣⋅∣2π 是模-2π2\pi2π 运算符,代表相位折叠。随着 ωT\omega_TωT 步进遍历工作带宽,ϕLIA\phi{\text{LIA}}ϕLIA 被测量和记录。我们通常不关心常数相位偏移 ϕIF\phi_{\text{IF}}ϕIF,在成像应用中,这个常数相位项不影响重建图像的幅度,可以忽略。因此最终方程直接将目标距离映射到LIA的折叠相位。假设目标与TX和RX等距(即 rT=rR=rr_T = r_R = rrT=rR=r),其相对于某起始位置的距离可由解折叠相位 ϕ~LIA\tilde{\phi}_{\text{LIA}}ϕ~LIA 确定:
r=c2ωTϕ~LIA(5)r = \frac{c}{2\omega_T}\tilde{\phi}_{\text{LIA}} \tag{5}r=2ωTcϕ~LIA(5)
目标速度可从方程(3)的中频信号推导,该信号被送入频谱分析仪。在后向散射模式下,对信号总相位求导得到瞬时径向多普勒速度 vrv_rvr 与测量的频谱分析仪频率 ωSA\omega_{\text{SA}}ωSA 的关系:
vr=ωSA−ωIF2ωTc(6)v_r = \frac{\omega_{\text{SA}} - \omega_{\text{IF}}}{2\omega_T}c \tag{6}vr=2ωTωSA−ωIFc(6)
LIA测量信号的积分相位噪声(即均方根相位误差)由下式给出:
σϕ2=2N(f)SΔf(7)\sigma_\phi^2 = 2\frac{N(f)}{S}\Delta f \tag{7}σϕ2=2SN(f)Δf(7)
其中 N(f)N(f)N(f) 是噪声功率谱密度,SSS 是信号功率,Δf\Delta fΔf 是有效噪声带宽,等于 1/(4τ)1/(4\tau)1/(4τ),τ\tauτ 是LIA低通滤波器的用户定义时间常数。典型的LIA(如论文使用的SR844)允许设置时间常数直到数千秒。方程(7)中的因子2来自LIA将信号混频到直流时的双边带噪声。结合方程(5)和(7),可得理论距离精度与信噪比、LIA时间常数和TX频率的关系:
σr=c2ωTN(f)2τS(8)\sigma_r = \frac{c}{2\omega_T}\sqrt{\frac{N(f)}{2\tau S}} \tag{8}σr=2ωTc2τSN(f) (8)
该方程也符合直觉:距离精度随工作频率、LIA时间常数和信噪比的提高而改善。
电路级设计与实现
倍频器链与功率放大器
TX和RX在TSMC 65nm CMOS工艺中作为两个独立芯片制造。TX芯片包含TX信号的倍频器链和功率放大器(PA),RX芯片包含TX链的副本以及构成超外差架构的中频电路。设计目标是实现高带宽和高辐射功率,并向空气辐射(即正面辐射)而非向硅基底辐射------后者是常见做法。
如Fig. 1所示,单端输入信号(TX为15-16.875 GHz,RX为14.6875-16.5625 GHz)耦合进芯片后由输入变压器巴伦转换为差分信号,然后经过三级级联倍频器。输入匹配网络与巴伦在第一级倍频器输入端对信号的二次谐波提供20 dB抑制,这对整个链路实现线性响应至关重要。倍频器偏置在最佳电流密度以最大化二次谐波功率。此外,为避免在各级之间使用巴伦,从倍频器晶体管的漏极和源极提取差分信号,这不仅节省面积还提高各级的提取功率。为进一步最大化二次谐波功率,在级间匹配网络变压器的中心抽头放置1 kΩ电阻。仿真表明,倍频器链在125 GHz向四路巴伦功分器提供4.3 dBm功率,3 dB带宽为15.6 GHz。
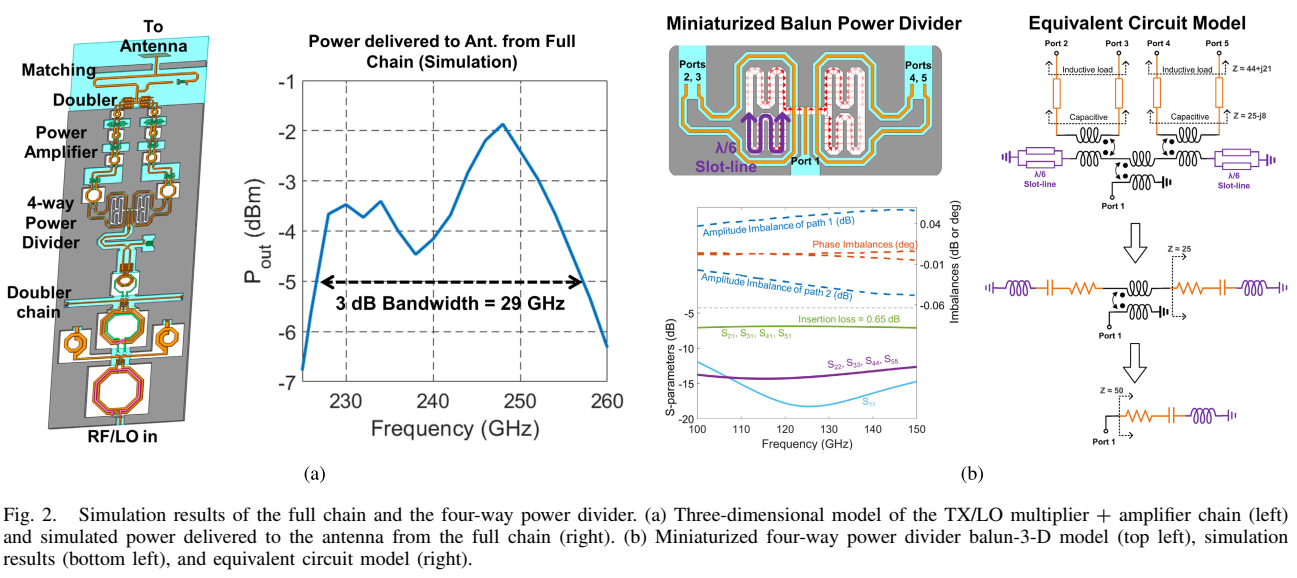
功分器后接三级PA进一步提升功率以驱动最后一级倍频器。PA每级采用中和差分共源放大器,偏置在0.3 mA/μm电流密度,实现9 dB增益,对于3 dBm输入功率实现6.8%的峰值功率附加效率(PAE)。交叉耦合中和与使用变压器的级间匹配网络相结合实现宽带响应。PA输出后接最后一级倍频器。为使布局紧凑,使用交叉结将PA连接到最后一级倍频器,这种结构在差分信号做直角转弯时保持每条路径长度相同非常有用。最后两级倍频器的输出合并并匹配到天线。最后一级倍频器和天线进行协同设计以最小化TX和RX芯片中匹配网络的复杂度。Fig. 2(a)展示了全链路的三维模型以及倍频器链和PA交付给天线的仿真功率,显示3 dB带宽为29 GHz。
微型化四路巴伦功分器
片上槽线巴伦两路功分器最早由Wang和Han提出。本文在两个方面扩展了他们的设计。首先,强制实施XY对称并提取四路输出而非两路,这种对称性产生了优异的幅度和相位平衡,在有限元仿真误差容限内------幅度不平衡小于0.05 dB,相位不平衡小于0.02°。其次,如Fig. 2(b)所示,蜿蜒槽线被微型化到 λ/6\lambda/6λ/6 长度。这种微型化有两方面帮助:减少槽线的辐射损耗------因为微型化谐振天线具有较小的辐射电阻;更容易匹配到下一级PA。
为更好理解,论文给出了所提四路功分器的等效电路模型,如Fig. 2(b)右侧所示。由于下一级是PA,巴伦的每个分支看向变压器输入并呈现感性负载。环绕蜿蜒槽线的长接地共面波导(GCPW)传输线将该感性负载变换为容性负载。GCPW到槽线的过渡建模为理想变压器,将容性负载与蜿蜒槽线串联。将蜿蜒槽线从 λ/4\lambda/4λ/4 减小到 λ/6\lambda/6λ/6 使其呈感性,现在与容性负载形成串联RLC谐振器。本质上,作者微型化了蜿蜒槽线并将产生的电感作为到下一级匹配的一部分。等效电路模型中的电阻代表传递到下一级的功率而非电路损耗。由于谐振是串联RLC网络,为获得更宽带宽,电感应减小而电容应增大。这通过两条蜿蜒槽线的并联组合实现,有效地将串联呈现的电感减半。最后的槽线到微带过渡作为另一个变压器,将两个分支串联组合并呈现给输入。适当设计线和槽的尺寸可产生宽带匹配,具有非常低的插入损耗(0.65 dB)和优异的相位幅度平衡。仿真结果显示,在以125 GHz为中心的50 GHz超宽带宽内,各输出端口的S参数(S21S_{21}S21, S31S_{31}S31, S41S_{41}S41, S51S_{51}S51)接近-6 dB(理想四路功分),幅度不平衡和相位不平衡极小。
SIW双槽天线
目前大多数宽带片上天线向硅基底辐射,需要昂贵的硅透镜且需精确对准。正面辐射的集成天线不需要任何透镜,但带宽受限于给定工艺中可用的金属堆叠厚度。使用交叉槽SIW腔体槽天线的带宽增强方法已在文献中提出,但交叉槽设计的缺点是天线极化在频带内从v变化到h,这是不理想的,因为实际目标通常具有极化相关的相位响应。
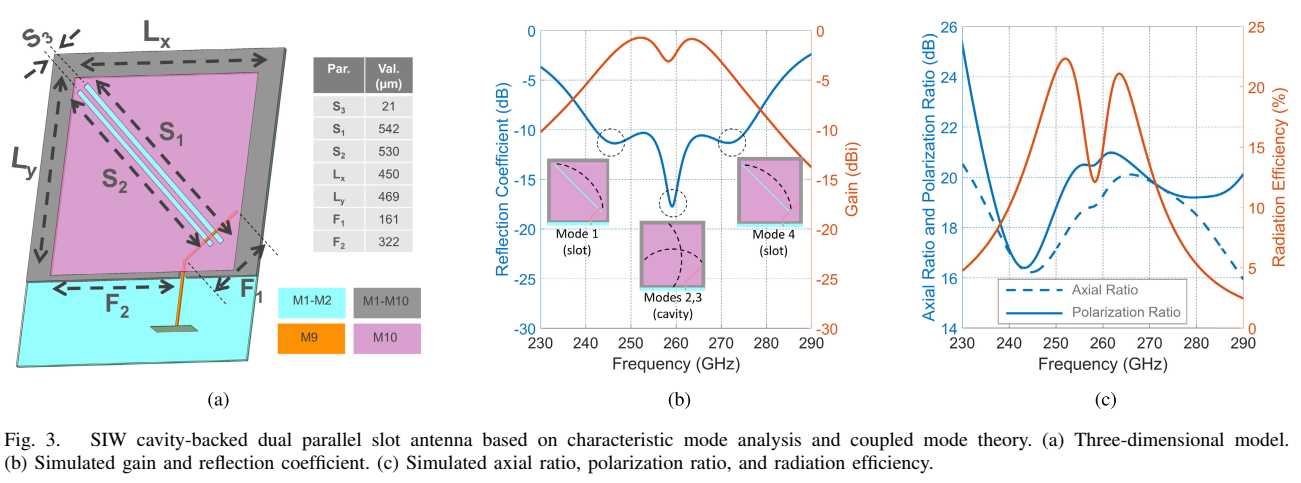
本文提出的天线由一对平行槽组成,由SIW腔体支撑并由带状线馈电,在整个频带内实现稳定的固定极化。如Fig. 3(a)所示,天线结构包含七个关键设计参数:S3S_3S3(21 μm)、S1S_1S1(542 μm)、S2S_2S2(530 μm)、LxL_xLx(450 μm)、LyL_yLy(489 μm)、F1F_1F1(161 μm)和F2F_2F2(322 μm)。与文献[10]中的交叉槽相比,所提天线具有等长槽。由于槽等长,单独时各自呈现相同的谐振。然而当槽相邻放置时,它们之间的强耦合导致谐振分裂,也称为模式分裂。
实际上,该结构呈现四个耦合谐振:两个辐射"槽"模式和两个非辐射"腔"模式。槽之间的间距决定两个辐射槽模式的分离,它们的长度决定其绝对频率(一阶近似)。为实现最大可能带宽,论文将腔模式置于辐射槽模式之间,这增强了输入匹配带宽而不使整个频带内的法向增益低于-3 dB。如Fig. 3(b)所示,反射系数在Mode 1(槽模式)、Modes 2,3(腔模式)和Mode 4(槽模式)处呈现谐振,增益在整个230-290 GHz范围内保持在-5 dB以上。另一种策略是将腔模式置于辐射模式之外,这适用于需要尖锐带外频率截止的情况,如频率梳应用。使用Nelder-Mead非线性优化器将两个腔模式置于两个辐射槽模式之间,优化在标注的七个参数上进行。
由于槽是平行的,在整个先进的30 GHz(12%)带宽内保持了高极化比和轴比。如Fig. 3©所示,轴比在整个频带内保持在14-26 dB之间,极化比超过18 dB,辐射效率约为5-20%。这种天线的主要优势是可以轻松缩放到不同频段和制造工艺。适当设计和放置模式可以提供宽带宽和/或尖锐的带外滚降。然而,SIW腔体顶层和底层金属之间的有限间距在向低频移动时限制了带宽。据作者所知,这种由带状线馈电的双平行槽SIW天线设计是新颖的,在现有天线文献中未见报道,包括片外PCB实现。
接收机与中频链路
在RX链中,接收信号送入单端平方律混频器下变频到5 GHz。混频器栅极偏置在阈值电压以下以优化其变频增益和噪声系数(从而优化SNR),对应-1.8 dBm的LO功率。混频器后接与混频器噪声匹配的两级低噪声放大器。第二个混频器进一步将信号下变频到10 MHz。接收机对250 GHz输入接收信号的仿真功率增益为8 dB,噪声系数为14.7 dB。
测量结果
发射机与接收机测量
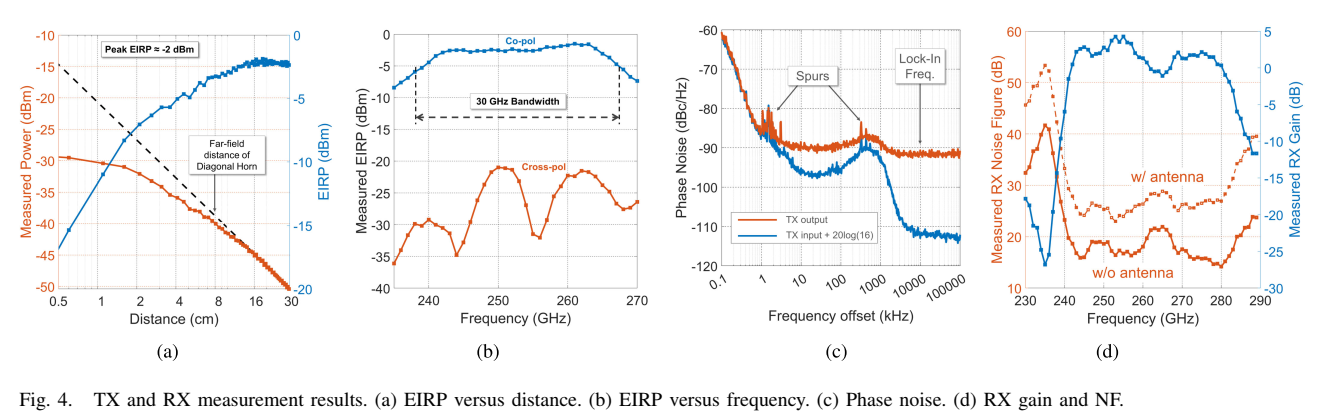
TX和RX的测量结果如Fig. 4所示。EIRP使用Erickson PM-4功率计测量,将其放在线性平台上并增加距离直到接收功率遵循Friis传输方程。如Fig. 4(a)所示,在距离约8 cm处进入远场区域,测量功率与对角喇叭天线的远场距离一致。实现的峰值EIRP为-2 dBm,略高于仿真,可能是由于天线金属损耗使用了过于保守的值以及PCB大型金属地平面增加了天线增益。如Fig. 4(b)所示,测量的同极化EIRP在30 GHz带宽内保持在-5 dBm以上,交叉极化EIRP显示了整个频带内的高极化纯度,低于同极化约20 dB。
TX相位噪声使用Rohde & Schwarz FSW信号分析仪和外部谐波混频器测量。如Fig. 4©所示,TX芯片信号的相位噪声在从芯片辐射的256 GHz和进入芯片的16 GHz两处测量。16 GHz信号的相位噪声按TX链的倍频因子放大,即加上 20log(16)20\log(16)20log(16) 因子。两次测量的差给出TX链的附加相位噪声。在10 MHz锁相频率处附加相位噪声约为20 dB。该图也清楚展示了锁相架构的主要优势之一:由于锁相频率在整个RF带宽内固定,可选择它来避开IF频谱中的杂散。
RX功率增益使用LIA和TX芯片作为源测量。由于TX EIRP已知,通过测量LIA接收的功率求得RX增益。RX噪声系数基于增益法用频谱分析仪计算。如Fig. 4(d)所示,最小噪声系数约为15 dB(不含天线损耗)和25 dB(含仿真的天线损耗),RX增益约为-15至-25 dB。
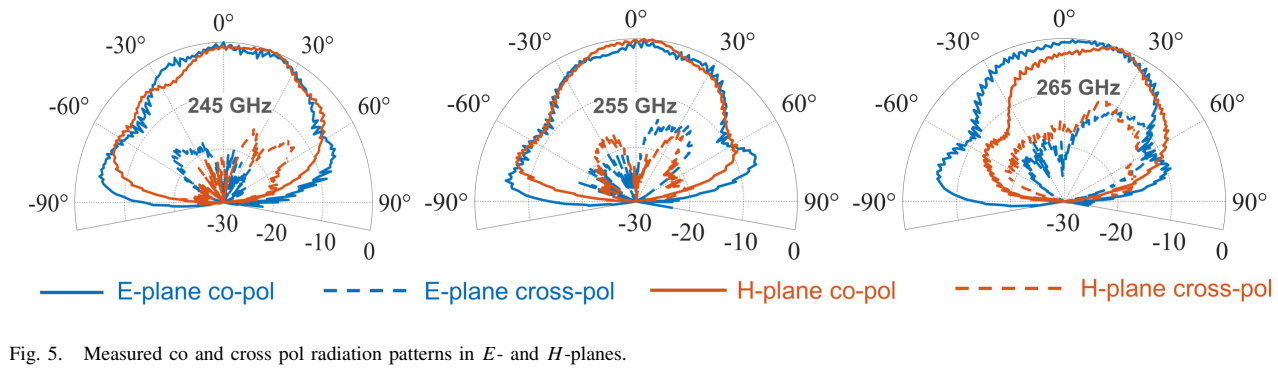
片上天线的归一化同极化和交叉极化辐射方向图在E面和H面测量,使用频谱分析仪、外部混频器、TX芯片和旋转平台。结果如Fig. 5所示,分别展示了245 GHz、255 GHz和265 GHz三个频点的方向图。半功率波束宽度在整个频带内约为60°,交叉极化功率在大部分频带内低于同极化20 dB以上。如此宽的波束宽度对于近场SAR成像是理想的,确保目标被合成阵列的每个元素照射。这也使双基地雷达更容易,因为TX和RX之间的波束重叠度很高。低天线增益由SAR的高处理增益补偿------直观理解是,更宽的天线波束意味着更多的合成元素照射给定目标,虽然每个天线接收的信号功率较低,但当来自更大合成阵列的信号相干相加时,噪底也降低相同的量------这就是SAR的动态范围和分辨率与天线增益无关的原因。
雷达系统组装与测试配置
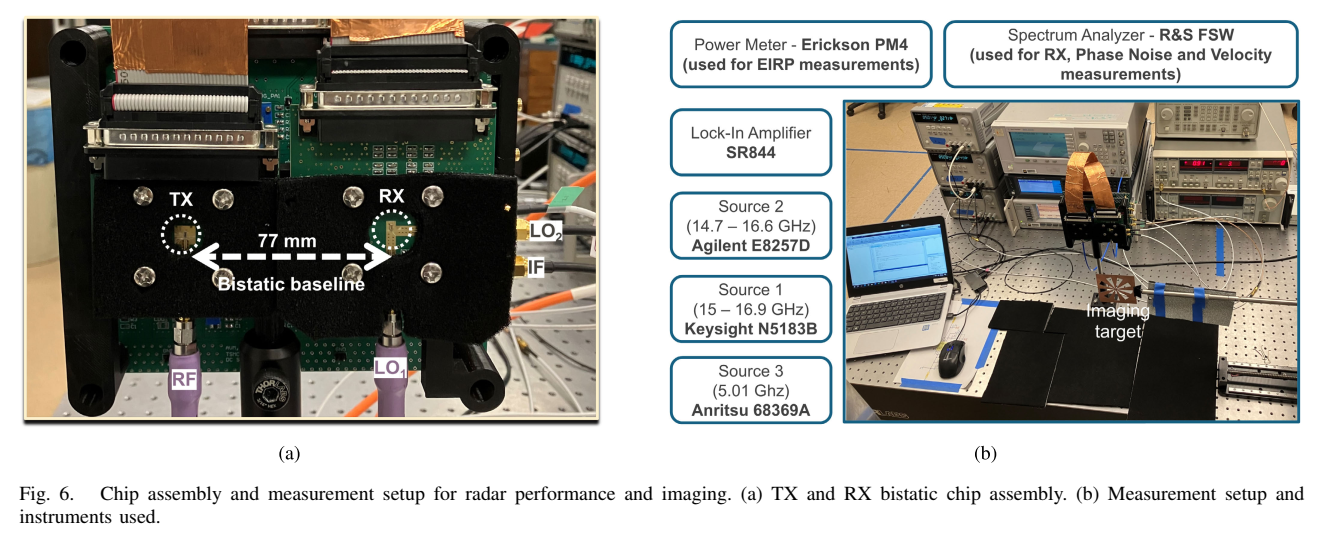
雷达系统按双基地配置组装用于雷达性能和成像实验,如Fig. 6所示。Fig. 6(a)展示了TX和RX双基地芯片组装,TX和RX芯片间距77 mm(即双基地基线)。Fig. 6(b)展示了测量设置和使用的仪器,包括:Erickson PM-4功率计(用于EIRP测量)、Rohde & Schwarz FSW频谱分析仪(用于RX、相位噪声和速度测量)、SR844锁相放大器、Keysight N5183B信号源1(15-16.9 GHz)、Agilent E8257D信号源2(14.7-16.6 GHz)和Anritsu 68369A信号源3(5.01 GHz)。成像目标放置在精密XY平台上。
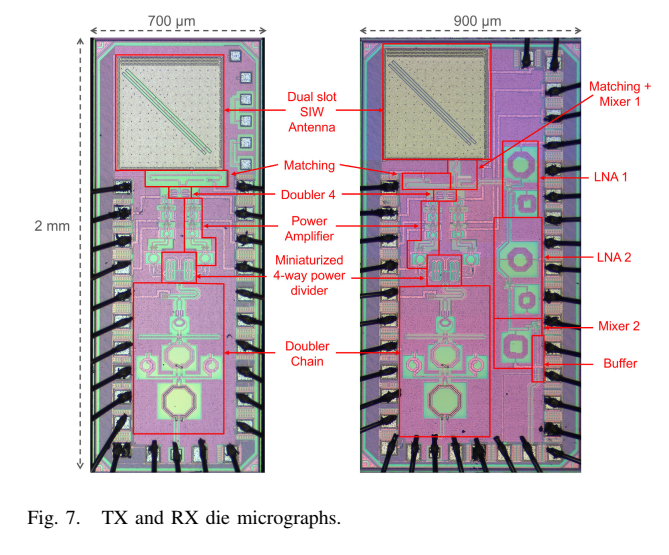
TX和RX芯片的制造芯片照片如Fig. 7所示。TX芯片尺寸为700 μm × 2 mm,包含双槽SIW天线、匹配网络、第四级倍频器、功率放大器、微型化四路功分器和倍频器链。RX芯片尺寸为900 μm × 2 mm,包含匹配+混频器1、LNA1、LNA2、混频器2和缓冲器。为测试TX-RX隔离度,在雷达指向大型吸波表面时分别测量TX开启和关闭时的RX信号。注意确保附近没有散射体,使到达RX的唯一信号是泄漏信号。选择77 mm的间距以确保开和关的测量相似,表明几乎没有直接泄漏。TX和RX芯片之间放置额外的吸波材料以进一步提高隔离度。
雷达性能测量
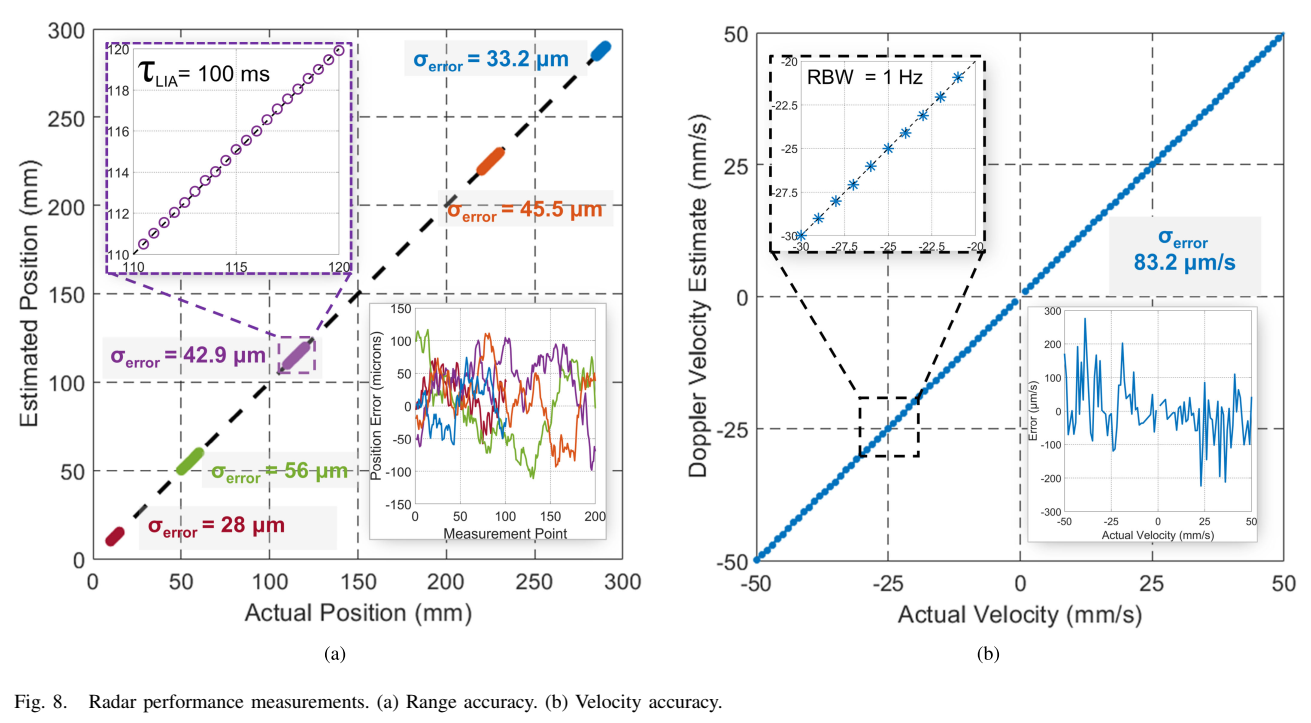
Fig. 8展示了雷达性能测量结果。距离精度和速度精度通过将4×4英寸的平面金属板(角反射器具有更高的RCS但不能用于双基地雷达,因为其双基地RCS方向图很窄)平行于TX-RX系统放置,并在精密线性平台上沿法向远离系统移动来测量。锁相信号的测量相位被解折叠并根据方程(5)映射到距离。
如Fig. 8(a)所示,在三种不同的LIA时间常数(100 ms、中等、和较短)设置下进行了测量。噪声功率谱密度测量约为-110 dBm/Hz,当LIA时间常数设为10 ms时信号功率为-83 dBm。由方程(8)得到的理论距离精度约为30 μm。测量的距离精度约为40 μm(σerror\sigma_{\text{error}}σerror = 28 μm, 42.9 μm, 56 μm对应不同设置),最大距离误差小于110 μm(如嵌入图所示,位置误差在±150 μm范围内波动),表明与理论吻合良好。
如Fig. 8(b)所示,速度测量通过记录频谱分析仪上IF频率的多普勒频移(根据方程(6))完成,频谱分析仪设置为1 Hz分辨率带宽(RBW)。测量的速度精度约为80 μm/s(σerror\sigma_{\text{error}}σerror = 83.2 μm/s),峰值速度误差为275 μm/s(如嵌入图所示,误差在±300 μm/s范围内)。容易证明对于1 Hz分辨率带宽,速度误差应低于 (c/4ωT)(c/4\omega_T)(c/4ωT),即约50 μm/s。测量误差较高,可能是因为使用的线性平台保证精确位置控制但不保证精确速度控制。
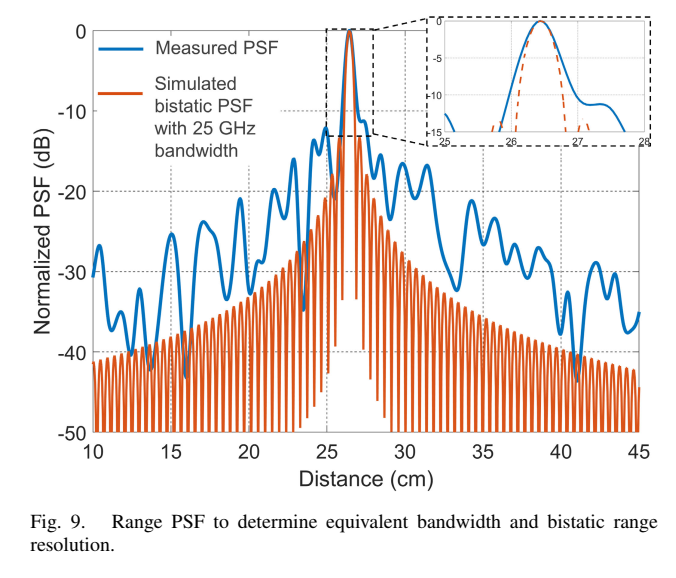
双基地系统的距离分辨率没有良好定义(即 ≠c/2BW\neq c/2BW=c/2BW),因为存在两个相位中心。例如,沿TX和RX连线的距离分辨率是无限的,因为该线上所有点具有相同的"距离"。注意双基地系统中等距离面是椭球而非球面。在双基地基线的远场,相位中心可近似为TX和RX的中点,距离分辨率可独立于距离定义。然而对于该系统,77 mm基线对应的远场距离约为10 m,使这种测量不切实际。因此,论文通过比较测量的点扩散函数(PSF)与仿真的PSF来演示距离性能,如Fig. 9所示。仿真PSF基于具有25 GHz 3 dB带宽的相同双基地系统。比较两个结果显示良好吻合,主瓣和旁瓣结构一致,表明雷达具有约25 GHz的3 dB带宽。
高分辨率相干成像实验
论文最后展示了高分辨率相干成像作为所提太赫兹雷达架构的潜在应用。相干成像指使用信号相位重建图像的成像技术(如SAR、ISAR、层析成像和全息术),而非仅使用幅度的非相干技术(如焦平面成像)。相干成像是更强大的技术,因为它提供更高的处理增益并可同时聚焦三维场景中的所有点,不需要任何精确对准的透镜系统,还提供场景的相位信息以提取目标的附加特征。成功的相干成像实现在片上太赫兹系统中很少被演示,据作者所知,没有200 GHz以上的CMOS芯片演示过相干成像(100 GHz以上也没有CMOS演示,但有一些工作在其他工艺如硅锗SiGe中演示了相干成像)。
首批成像实验在平面金属目标上进行。使用具有不同直径五个圆孔的目标和西门子星形模板测试系统的相位精度和长期相位相干性维持能力。目标安装在精密XY平台上,在横向平面内移动以收集60×60 mm网格上步进0.6 mm的逆SAR(ISAR)数据。原始数据使用后向投影处理重建图像,这是可能的,因为相位和目标距离如方程(5)所示具有直接线性关系。图像未做进一步处理。

目标和结果图像如Fig. 10所示。五圆孔目标(最小直径1 mm)的照片和雷达图像显示,图像对比度和边缘清晰度优异,表明近乎完美的相位重建。西门子星形模板的中心特征(小于1 mm)也被清晰分辨。完美相位重建下的理论横向分辨率约为 λ/2\lambda/2λ/2,在该频段约为0.6 mm。由于1 mm直径的最小孔在重建图像中清晰分辨,论文得出结论:所提系统工作在分辨率极限。这也由西门子星形图像的中心验证,那里的特征尺寸小于1 mm。
接下来使用两个真实目标:软盘和涂铜漆金属化的3D打印手枪。软盘图像揭示了内部磁盘和肉眼不可见的其他几个特征,从而演示了无损检测作为可行应用。手枪图像质量和分辨率也是前所未有的,显示了手柄和枪管上的多个精细特征。扳机处于略微不同的距离分格(trigger range bin),改变距离分格后可见其完全聚焦。
性能比较与结论
Table I给出了与其他最近先进太赫兹雷达系统的比较。该系统在242-267 GHz频段工作,25 GHz带宽,正面辐射,分辨率约6 mm(针对大基线双基地系统使用 R=c/2BWR=c/2BWR=c/2BW 计算),是唯一演示成像的系统,EIRP为-2 dBm,最小噪声系数15 dB,直流功耗TX 240 mW、RX 290 mW,芯片尺寸TX 1.4 mm²、RX 1.8 mm²,采用65nm CMOS工艺。与其他工作相比,该系统在多个维度实现了竞争性或领先的性能。
| 参数 | JSSC 2021 | T-THz 2018 | ISSCC 2024 | JSSC 2022 | ISSCC 2021 | T-MTT 2023 | T-THz 2022 | 本工作 |
|---|---|---|---|---|---|---|---|---|
| 频率(GHz) | 220-320 | 305-375 | 230-246 | 134-148 | 191-257.7 | 223-288 | 450-490 | 242-267 |
| 带宽(GHz) | 100^(1) | 70 | 16 | 14 | 66.7 | 65 | 40 | 25 |
| 辐射方向 | 正面 | 正面 | 背面 | 正面^(2) | 背面 | 背面 | 正面 | 正面 |
| 分辨率(mm) | 1.5 | 2.1 | 9.4 | 10.7 | 2.2 | 2.3 | 3.7 | 6^(4) |
| 成像演示 | 否 | 否 | 否 | 否 | 是^(5) | 否 | 否 | 是 |
| EIRP(dBm) | -2.5^(6) | 18.4^(7) | 16.2^(7) | 25.2^(7) | 17^(7) | -5.4 | -12 | -2 |
| 最小NF(dB) | 22.2^(8) | 19.7 | NA | 12.9 | NA | 23.5 | 36.3 | 15 |
| 直流功耗(mW) | 840 | 1700 | 186 | 405 | 68 | 305 | 280 | TX:240, RX:290 |
| 芯片尺寸(mm²) | 5 | 2.85 | 0.42 | 3.1 | 0.22 | 3.3 | 1.42 | TX:1.4, RX:1.8 |
| 工艺 | 65nm CMOS | 130nm SiGe | 55nm SiGe | 65nm CMOS | 55nm SiGe | 130nm SiGe | 90nm SiGe | 65nm CMOS |
注:(1)频率梳架构,每通道带宽20 GHz;(2)片外PCB地;(3)使用R=c/2BWR=c/2BWR=c/2BW计算;(4)双基地距离分辨率对大基线未良好定义;(5)非相干重建;(6)单通道EIRP;(7)含透镜;(8)含天线损耗。
尽管太赫兹FMCW雷达系统已在文献中演示,但关于相干成像雷达的实验结果论文并不常见。缺乏发展的主要原因之一是相干成像需要非常好的相位精度和长期相位相干性。本文论证了FMCW雷达,特别是在太赫兹频率,对于此类应用并不理想,并提出了一种以相位精度和相干性为核心的替代架构。论文强调了所提架构的系统级优缺点,并在65nm标准CMOS工艺中实现电路。首先测量TX和RX芯片并证明具有先进性能;接着测量雷达系统的距离和速度精度并证明与理论良好吻合;最后使用多个目标测试系统的高分辨率成像能力,每个目标的特征都接近理论分辨率极限,系统都能够分辨。
鉴于独立的TX和RX芯片,存在几个可能的未来方向:带透镜的透射测量系统可用于进行相干光谱学;可实现多输入多输出(MIMO)系统以加快成像速度;可开发准单基地双反射器系统用于实时成像。
附录:数学推导
A. 超外差雷达信号模型的完整推导
本节详细推导从TX信号到LIA输出的完整信号路径。
TX辐射信号 :TX信号源产生频率为f1f_1f1的信号,经×16倍频后辐射:
sTX(t)=ATcos(ωTt+ϕT),ωT=16×2πf1s_{TX}(t) = A_T \cos(\omega_T t + \phi_T), \quad \omega_T = 16 \times 2\pi f_1sTX(t)=ATcos(ωTt+ϕT),ωT=16×2πf1
自由空间传播 :信号从TX传播到目标再到RX,总路径长度为rT+rRr_T + r_RrT+rR。传播引入的相位延迟为:
Δϕprop=ωTc(rT+rR)=2πfTc(rT+rR)=kT(rT+rR)\Delta\phi_{prop} = \frac{\omega_T}{c}(r_T + r_R) = \frac{2\pi f_T}{c}(r_T + r_R) = k_T(r_T + r_R)Δϕprop=cωT(rT+rR)=c2πfT(rT+rR)=kT(rT+rR)
其中kT=2π/λTk_T = 2\pi/\lambda_TkT=2π/λT是波数。接收信号为:
sRX,received(t)=ARXcos(ωTt+ϕT−ωTc(rT+rR))s_{RX,received}(t) = A_{RX} \cos\left(\omega_T t + \phi_T - \frac{\omega_T}{c}(r_T + r_R)\right)sRX,received(t)=ARXcos(ωTt+ϕT−cωT(rT+rR))
第一次混频 :接收信号与本地RX信号sR=ARcos(ωRt+ϕR)s_R = A_R\cos(\omega_R t + \phi_R)sR=ARcos(ωRt+ϕR)混频。利用三角恒等式cosαcosβ=12[cos(α−β)+cos(α+β)]\cos\alpha\cos\beta = \frac{1}{2}[\cos(\alpha-\beta) + \cos(\alpha+\beta)]cosαcosβ=21[cos(α−β)+cos(α+β)]:
sRX,received⋅sR=ARXAR2[cos((ωT−ωR)t+ϕT−ϕR−ωTc(rT+rR))+cos((ωT+ωR)t+...)]s_{RX,received} \cdot s_R = \frac{A_{RX}A_R}{2}\left[\cos\left((\omega_T-\omega_R)t + \phi_T - \phi_R - \frac{\omega_T}{c}(r_T+r_R)\right) + \cos\left((\omega_T+\omega_R)t + ...\right)\right]sRX,received⋅sR=2ARXAR[cos((ωT−ωR)t+ϕT−ϕR−cωT(rT+rR))+cos((ωT+ωR)t+...)]
低通滤波保留差频项,得到第一中频信号(5 GHz):
sIF1(t)=AIF1cos((ωT−ωR)t+ϕT−ϕR−ωTc(rT+rR))s_{IF1}(t) = A_{IF1}\cos\left((\omega_T-\omega_R)t + \phi_T - \phi_R - \frac{\omega_T}{c}(r_T+r_R)\right)sIF1(t)=AIF1cos((ωT−ωR)t+ϕT−ϕR−cωT(rT+rR))
其中ωT−ωR=2π×5\omega_T - \omega_R = 2\pi \times 5ωT−ωR=2π×5 GHz。
参考路径生成 :同时,TX和RX信号的副本在芯片外混频产生5 GHz参考信号,然后与LO信号(频率ωLO\omega_{LO}ωLO,设计使得最终IF为ωIF=2π×10\omega_{IF} = 2\pi \times 10ωIF=2π×10 MHz)混频。参考路径信号为:
sref(t)=Arefcos(ωIFt+ϕref)s_{ref}(t) = A_{ref}\cos(\omega_{IF}t + \phi_{ref})sref(t)=Arefcos(ωIFt+ϕref)
第二次混频 :sIF1s_{IF1}sIF1经LNA放大后与频率为(ωT−ωR+ωIF)(\omega_T - \omega_R + \omega_{IF})(ωT−ωR+ωIF)的信号混频。设该信号为sLO2(t)=cos((ωT−ωR+ωIF)t+ϕLO2)s_{LO2}(t) = \cos((\omega_T-\omega_R+\omega_{IF})t + \phi_{LO2})sLO2(t)=cos((ωT−ωR+ωIF)t+ϕLO2),则:
sIF1⋅sLO2→AIF12cos(ωIFt−ϕIF−ωTc(rT+rR))s_{IF1} \cdot s_{LO2} \rightarrow \frac{A_{IF1}}{2}\cos\left(\omega_{IF}t - \phi_{IF} - \frac{\omega_T}{c}(r_T+r_R)\right)sIF1⋅sLO2→2AIF1cos(ωIFt−ϕIF−cωT(rT+rR))
其中ϕIF=ϕLO2−ϕT+ϕR\phi_{IF} = \phi_{LO2} - \phi_T + \phi_RϕIF=ϕLO2−ϕT+ϕR是常数相位偏移。这就得到了方程(3)。
B. 距离精度的理论推导
相位测量与距离关系 :从方程(4)和(5),目标距离由相位测量确定:
r=c2ωTϕ~LIAr = \frac{c}{2\omega_T}\tilde{\phi}_{LIA}r=2ωTcϕ~LIA
取微分得距离误差与相位误差的关系:
σr=c2ωTσϕ\sigma_r = \frac{c}{2\omega_T}\sigma_\phiσr=2ωTcσϕ
相位噪声分析 :LIA本质上是一个窄带相干检测器。考虑输入信号s(t)=Acos(ωIFt+ϕ)s(t) = A\cos(\omega_{IF}t + \phi)s(t)=Acos(ωIFt+ϕ)加上噪声n(t)n(t)n(t)。LIA通过与参考信号cos(ωIFt)\cos(\omega_{IF}t)cos(ωIFt)和sin(ωIFt)\sin(\omega_{IF}t)sin(ωIFt)相乘并低通滤波,提取同相和正交分量:
I=Acosϕ+nI,Q=Asinϕ+nQI = A\cos\phi + n_I, \quad Q = A\sin\phi + n_QI=Acosϕ+nI,Q=Asinϕ+nQ
其中nIn_InI和nQn_QnQ是滤波后的噪声分量。相位估计为ϕ^=arctan(Q/I)\hat{\phi} = \arctan(Q/I)ϕ^=arctan(Q/I)。
在高信噪比条件下,相位误差近似为:
δϕ≈nQcosϕ−nIsinϕA\delta\phi \approx \frac{n_Q\cos\phi - n_I\sin\phi}{A}δϕ≈AnQcosϕ−nIsinϕ
因此相位方差为:
σϕ2=σn2A2=N(f)ΔfS\sigma_\phi^2 = \frac{\sigma_n^2}{A^2} = \frac{N(f)\Delta f}{S}σϕ2=A2σn2=SN(f)Δf
其中N(f)N(f)N(f)是噪声功率谱密度,S=A2/2S = A^2/2S=A2/2是信号功率,Δf\Delta fΔf是有效噪声带宽。
LIA低通滤波器特性 :LIA使用时间常数为τ\tauτ的低通滤波器,其传递函数为H(f)=1/(1+j2πfτ)H(f) = 1/(1+j2\pi f\tau)H(f)=1/(1+j2πfτ)。等效噪声带宽为:
Δf=∫0∞∣H(f)∣2df=∫0∞11+(2πfτ)2df=14τ\Delta f = \int_0^\infty |H(f)|^2 df = \int_0^\infty \frac{1}{1+(2\pi f\tau)^2}df = \frac{1}{4\tau}Δf=∫0∞∣H(f)∣2df=∫0∞1+(2πfτ)21df=4τ1
双边带噪声修正 :由于混频过程将正负频率的噪声都折叠到基带,需要乘以因子2:
σϕ2=2N(f)S⋅14τ=N(f)2τS\sigma_\phi^2 = 2\frac{N(f)}{S}\cdot\frac{1}{4\tau} = \frac{N(f)}{2\tau S}σϕ2=2SN(f)⋅4τ1=2τSN(f)
结合距离-相位关系,得到最终的距离精度表达式:
σr=c2ωTN(f)2τS\sigma_r = \frac{c}{2\omega_T}\sqrt{\frac{N(f)}{2\tau S}}σr=2ωTc2τSN(f)
数值验证 :论文测量N(f)=−110N(f) = -110N(f)=−110 dBm/Hz =10−14= 10^{-14}=10−14 mW/Hz,S=−83S = -83S=−83 dBm =5×10−12= 5\times10^{-12}=5×10−12 mW,τ=10\tau = 10τ=10 ms,fT=256f_T = 256fT=256 GHz。代入得:
σr=3×1082×2π×256×10910−142×0.01×5×10−12≈30 μm\sigma_r = \frac{3\times10^8}{2\times2\pi\times256\times10^9}\sqrt{\frac{10^{-14}}{2\times0.01\times5\times10^{-12}}} \approx 30\ \mu\text{m}σr=2×2π×256×1093×1082×0.01×5×10−1210−14 ≈30 μm
与测量值40 μm吻合良好。
C. 速度测量原理推导
多普勒效应 :当目标以径向速度vrv_rvr运动时,接收信号的瞬时频率发生偏移。考虑目标距离随时间变化:r(t)=r0+vrtr(t) = r_0 + v_r tr(t)=r0+vrt。
接收信号的瞬时相位为:
Φ(t)=ωTt−ωTc(rT(t)+rR(t))\Phi(t) = \omega_T t - \frac{\omega_T}{c}(r_T(t) + r_R(t))Φ(t)=ωTt−cωT(rT(t)+rR(t))
对于后向散射(rT=rR=rr_T = r_R = rrT=rR=r):
Φ(t)=ωTt−2ωTc(r0+vrt)=ωT(1−2vrc)t−2ωTr0c\Phi(t) = \omega_T t - \frac{2\omega_T}{c}(r_0 + v_r t) = \omega_T\left(1 - \frac{2v_r}{c}\right)t - \frac{2\omega_T r_0}{c}Φ(t)=ωTt−c2ωT(r0+vrt)=ωT(1−c2vr)t−c2ωTr0
瞬时频率 :瞬时频率为相位对时间的导数:
ωinst=dΦdt=ωT(1−2vrc)\omega_{inst} = \frac{d\Phi}{dt} = \omega_T\left(1 - \frac{2v_r}{c}\right)ωinst=dtdΦ=ωT(1−c2vr)
IF信号频率 :经过混频后,IF信号频率变为:
ωSA=ωIF+ωT⋅2vrc=ωIF+ωDoppler\omega_{SA} = \omega_{IF} + \omega_T\cdot\frac{2v_r}{c} = \omega_{IF} + \omega_{Doppler}ωSA=ωIF+ωT⋅c2vr=ωIF+ωDoppler
求解速度:
vr=(ωSA−ωIF)c2ωTv_r = \frac{(\omega_{SA} - \omega_{IF})c}{2\omega_T}vr=2ωT(ωSA−ωIF)c
这就是方程(6)。
速度精度 :频谱分析仪的频率分辨率由分辨率带宽(RBW)决定。对于RBW = 1 Hz,频率测量不确定度δf≈1\delta f \approx 1δf≈1 Hz。因此速度不确定度为:
δvr=δω⋅c2ωT=2π⋅1⋅3×1082×2π×256×109≈0.6 μm/s\delta v_r = \frac{\delta\omega \cdot c}{2\omega_T} = \frac{2\pi \cdot 1 \cdot 3\times10^8}{2 \times 2\pi \times 256\times10^9} \approx 0.6\ \mu\text{m/s}δvr=2ωTδω⋅c=2×2π×256×1092π⋅1⋅3×108≈0.6 μm/s
实际测量误差(~80 μm/s)较大,主要来自线性平台的速度控制精度。
D. 双基地雷达几何与分辨率分析
等距离面 :对于双基地雷达,满足rT+rR=constr_T + r_R = \text{const}rT+rR=const的点构成以TX和RX为焦点的椭球面。设TX和RX位于(±d/2,0,0)(\pm d/2, 0, 0)(±d/2,0,0),基线长度d=77d = 77d=77 mm,则等距离面方程为:
(x+d/2)2+y2+z2+(x−d/2)2+y2+z2=2a\sqrt{(x+d/2)^2 + y^2 + z^2} + \sqrt{(x-d/2)^2 + y^2 + z^2} = 2a(x+d/2)2+y2+z2 +(x−d/2)2+y2+z2 =2a
其中2a=rT+rR2a = r_T + r_R2a=rT+rR是椭球长轴。
距离分辨率的方向依赖性 :距离分辨率定义为能分辨的最小Δ(rT+rR)\Delta(r_T + r_R)Δ(rT+rR)。在不同方向上,这对应不同的空间分辨率。沿基线方向(xxx轴),所有点都满足rT+rR=dr_T + r_R = drT+rR=d,因此距离分辨率为无穷大。沿垂直于基线的方向(zzz轴),对于远离基线的点,rT≈rRr_T \approx r_RrT≈rR,此时距离分辨率接近单基地情况Δr≈c/(2BW)\Delta r \approx c/(2BW)Δr≈c/(2BW)。
远场近似 :当目标距离R≫d2/λR \gg d^2/\lambdaR≫d2/λ(远场条件)时,相位中心可近似为TX和RX的中点。此时:
rT+rR≈2R−d2sin2θ8R+O(R−2)r_T + r_R \approx 2R - \frac{d^2\sin^2\theta}{8R} + O(R^{-2})rT+rR≈2R−8Rd2sin2θ+O(R−2)
其中θ\thetaθ是目标相对于基线的角度。在远场,距离分辨率近似为c/(2BW)c/(2BW)c/(2BW)。
对于本系统,d=77d = 77d=77 mm,λ≈1.2\lambda \approx 1.2λ≈1.2 mm(在250 GHz),远场距离Rff=2d2/λ≈10R_{ff} = 2d^2/\lambda \approx 10Rff=2d2/λ≈10 m,这使得远场测量不切实际。
E. SAR/ISAR成像的后向投影重建
k空间采样 :步进频率雷达在k空间(波数空间)采样目标的散射函数。对于位于r0\mathbf{r}_0r0的点目标,在频率ω\omegaω处测量的复散射幅度为:
S(ω)=σexp(−jωc(rT+rR))S(\omega) = \sigma \exp\left(-j\frac{\omega}{c}(r_T + r_R)\right)S(ω)=σexp(−jcω(rT+rR))
其中σ\sigmaσ是目标散射系数。
图像重建 :后向投影算法通过对所有频率和所有合成孔径位置的测量数据进行相干叠加来重建图像。对于图像点r\mathbf{r}r:
I(r)=∑n∑mS(ωn,pm)exp(+jωnc(∣r−pT,m∣+∣r−pR,m∣))I(\mathbf{r}) = \sum_n \sum_m S(\omega_n, \mathbf{p}m) \exp\left(+j\frac{\omega_n}{c}(|\mathbf{r}-\mathbf{p}{T,m}| + |\mathbf{r}-\mathbf{p}_{R,m}|)\right)I(r)=n∑m∑S(ωn,pm)exp(+jcωn(∣r−pT,m∣+∣r−pR,m∣))
其中pm\mathbf{p}mpm是第mmm个合成孔径位置,pT,m\mathbf{p}{T,m}pT,m和pR,m\mathbf{p}_{R,m}pR,m分别是TX和RX位置。
分辨率分析 :横向(cross-range)分辨率由合成孔径长度LLL决定:
δcr=λR2L\delta_{cr} = \frac{\lambda R}{2L}δcr=2LλR
对于近场成像,当L≫λL \gg \lambdaL≫λ时,可实现δcr≈λ/2\delta_{cr} \approx \lambda/2δcr≈λ/2的衍射极限分辨率。对于λ≈1.2\lambda \approx 1.2λ≈1.2 mm,理论极限为0.6 mm,与论文的实验结果一致。
距离分辨率由带宽BWBWBW决定(在远场近似下):
δr=c2BW\delta_r = \frac{c}{2BW}δr=2BWc
对于BW=25BW = 25BW=25 GHz,δr=6\delta_r = 6δr=6 mm。
F. SIW腔体天线的特征模分析
特征模理论基础 :导体结构的特征模由以下广义特征值方程定义:
XJn=λnRJnX\mathbf{J}_n = \lambda_n R\mathbf{J}_nXJn=λnRJn
其中RRR和XXX分别是阻抗算子Z=R+jXZ = R + jXZ=R+jX的实部和虚部,Jn\mathbf{J}_nJn是第nnn个特征电流,λn\lambda_nλn是对应的特征值。
模式重要性 :特征值λn\lambda_nλn决定模式的辐射特性。当λn=0\lambda_n = 0λn=0时,模式谐振;λn>0\lambda_n > 0λn>0时,模式呈感性(存储磁能);λn<0\lambda_n < 0λn<0时,模式呈容性(存储电能)。模式重要性(Modal Significance)定义为:
MSn=1∣1+jλn∣MS_n = \frac{1}{|1 + j\lambda_n|}MSn=∣1+jλn∣1
在谐振频率处MSn=1MS_n = 1MSn=1。
耦合模分析 :对于双槽结构,当两个等长槽靠近时,它们的本征模发生耦合。设单槽的谐振频率为ω0\omega_0ω0,耦合系数为κ\kappaκ,则耦合系统的谐振频率分裂为:
ω±=ω0±κ\omega_\pm = \omega_0 \pm \kappaω±=ω0±κ
这解释了为什么双平行槽结构能在比单槽更宽的频带内保持良好的辐射特性。通过调整槽间距可以控制κ\kappaκ,从而调整带宽。
G. 微型化功分器的阻抗分析
传输线变换 :长度为lll、特性阻抗为Z0Z_0Z0的传输线将负载阻抗ZLZ_LZL变换为输入阻抗:
Zin=Z0ZL+jZ0tan(βl)Z0+jZLtan(βl)Z_{in} = Z_0 \frac{Z_L + jZ_0\tan(\beta l)}{Z_0 + jZ_L\tan(\beta l)}Zin=Z0Z0+jZLtan(βl)ZL+jZ0tan(βl)
其中β=2π/λ\beta = 2\pi/\lambdaβ=2π/λ。
感性负载变换为容性负载 :PA输入呈现感性负载ZL=R+jωLZ_L = R + j\omega LZL=R+jωL。选择适当的GCPW线长度lll使得βl\beta lβl接近π/2\pi/2π/2(但不等于π/2\pi/2π/2),可将感性负载变换为容性:
Zin≈Z02ZL∗=Z02R−jωLZ_{in} \approx \frac{Z_0^2}{Z_L^*} = \frac{Z_0^2}{R - j\omega L}Zin≈ZL∗Z02=R−jωLZ02
当ωL≫R\omega L \gg RωL≫R时,ZinZ_{in}Zin呈容性。
串联RLC谐振 :微型化槽线(l<λ/4l < \lambda/4l<λ/4)呈现感性阻抗Zslot=jXLZ_{slot} = jX_LZslot=jXL。与容性负载ZC=−jXCZ_C = -jX_CZC=−jXC串联形成串联谐振:
Ztotal=Rrad+j(XL−XC)Z_{total} = R_{rad} + j(X_L - X_C)Ztotal=Rrad+j(XL−XC)
其中RradR_{rad}Rrad是槽线的辐射电阻。谐振条件XL=XCX_L = X_CXL=XC时,Ztotal=RradZ_{total} = R_{rad}Ztotal=Rrad,实现纯实数匹配。
带宽优化 :串联RLC网络的品质因数Q=ω0L/RQ = \omega_0 L/RQ=ω0L/R。带宽BW=f0/QBW = f_0/QBW=f0/Q。减小LLL(通过微型化)和增大CCC(通过并联两条槽线有效减半LLL)可降低QQQ,扩展带宽。这就是论文中功分器能在50 GHz超宽带宽内保持低插入损耗的理论基础。