复数乘法（C & Simulink）

0 前言

复数乘法是复数运算中最核心的运算之一。

给定两个复数：
Z1=a+biZ2=c+di \begin{aligned} Z_1 = a + bi\\ Z_2 = c + di \end{aligned} Z1=a+biZ2=c+di

它们的乘积定义为：
Z1∗Z2=(a+bi)(c+di)=(ac−bd)+(ad+bc)i \begin{aligned} Z_1*Z_2 = (a + bi)(c+di) = (ac-bd)+(ad+bc)i\\ \end{aligned} Z1∗Z2=(a+bi)(c+di)=(ac−bd)+(ad+bc)i

1 几何意义

复数可以表示为平面上的点，因此复数乘法有丰富的几何解释。

复数可以用极坐标表示为：
z=r(cosθ+isinθ)=reiθ \begin{aligned} z =r(cos \theta + isin\theta)=re^{i\theta}\\ \end{aligned} z=r(cosθ+isinθ)=reiθ
当两个复数相乘时：
z1z2=r1r2ei(θ1 +θ2)=r1r2 $cosθ(θ1 +θ2)+isinθ(θ1 +θ2)$ \begin{aligned} z_1z_2 =r_1r_2e^{i(\theta_1\ + \theta_2)}=r_1r_2 $cos \\theta(\\theta_1\\ + \\theta_2) + isin\\theta(\\theta_1\\ + \\theta_2)$ \\ \end{aligned} z1z2=r1r2ei(θ1 +θ2)=r1r2 $cosθ(θ1 +θ2)+isinθ(θ1 +θ2)$
因此，其几何性质为：

模相乘：结果复数的模等于两个复数模的乘积
角度相加：结果复数的幅角等于两个复数幅角的和

复数乘法可以看作：

缩放变换：模的乘积实现了缩放效果
旋转变换：幅角的相加实现了旋转效果

2 Simulink模型

2.1 用于仿真在MCU上运行的32位版本

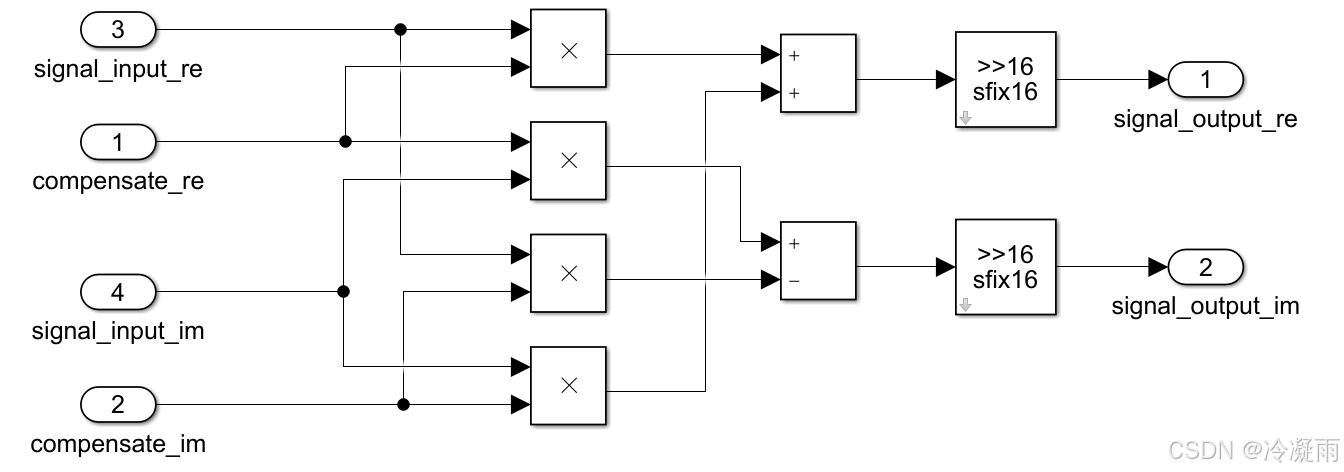
其中的>>16 sfix16是一个简单的子系统，代表右移之后，将其类型转换。

子系统的结构如下图所示：

实际运行如下图所示：

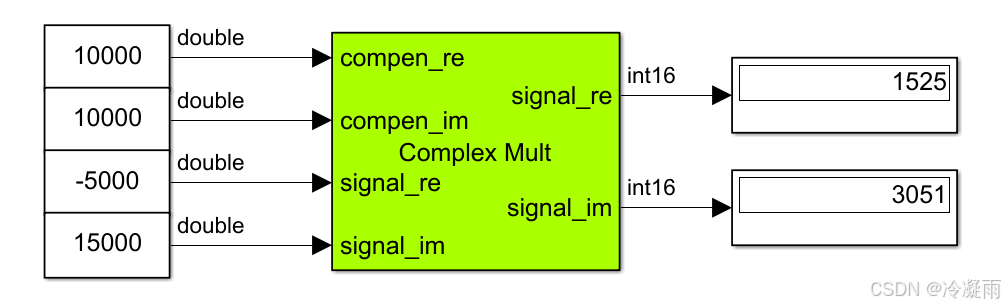
可以看出，这个实现方式因为将结果右移了16bit，会将结果缩小65535倍。

2.2 正常版本

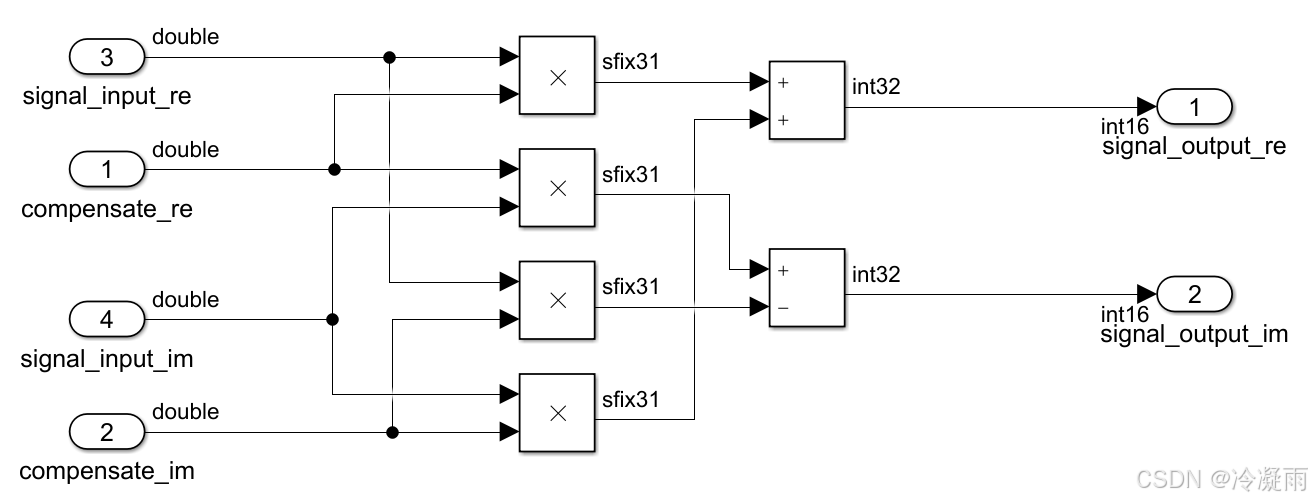
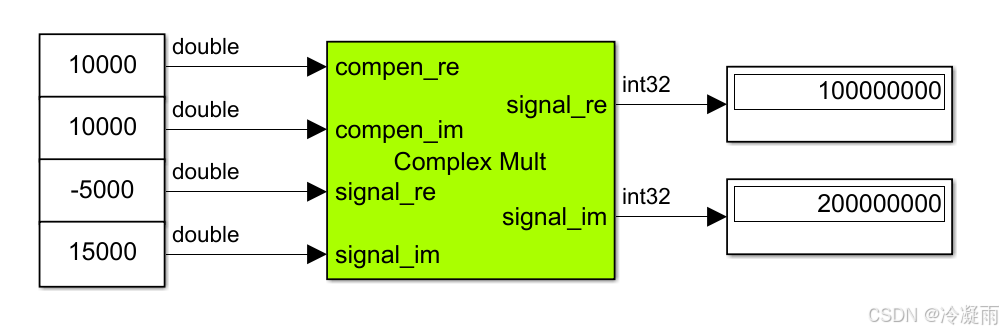
3 C语言源码

c 复制代码

#include "stdint.h"

/* 实部虚部类型 */
typedef struct
{
	int16_t Cos;
	int16_t Sin;
} SIN_T;

/*************************************************************************************
 * 名称: ComplexMult
 * 功能: 复数乘法
 * 输入: SIN_T in1 输入1
 *      SIN_T in2 输入2
 * 输出: SIN_T 输出
 **************************************************************************************/
__STATIC_FORCEINLINE SIN_T ComplexMult(SIN_T in1, SIN_T in2)
{
    SIN_T res;
    int32_t tempRe = 0, tempIm = 0;
    tempRe = (int32_t)(in1.Cos) * (int32_t)(in2.Cos) + (int32_t)(in1.Sin) * (int32_t)(in2.Sin);
    tempIm = (int32_t)(in1.Cos) * (int32_t)(in2.Sin) - (int32_t)(in1.Sin) * (int32_t)(in2.Cos);
    res.Cos = tempRe >> 16;
    res.Sin = tempIm >> 16;
    return res;
}