目录
[1. 能量函数 (Energy Function)](#1. 能量函数 (Energy Function))
[2. 联合概率分布](#2. 联合概率分布)
[3. 边缘与条件概率](#3. 边缘与条件概率)
五、训练算法:对比散度 (Contrastive Divergence, CD)
[CD-k 算法流程 (以 k=1 为例)](#CD-k 算法流程 (以 k=1 为例))
[CD-k 的关键思想](#CD-k 的关键思想)
[六、RBM 的变体](#六、RBM 的变体)
[七、RBM 的应用领域](#七、RBM 的应用领域)
[八、RBM 与其他模型的关系](#八、RBM 与其他模型的关系)
一、引言
限制性玻尔兹曼机 (Restricted Boltzmann Machine, RBM) 是一种生成式随机神经网络 ,属于概率图模型,由 Geoffrey Hinton 等人于 2006 年提出并推广。它是玻尔兹曼机的简化版本,具有二分图结构,能高效学习数据的概率分布,是深度学习早期的重要模型,也是 "深度信念网络 (DBN)" 的核心构建模块。
二、基本定义与核心特点
RBM 是一种两层神经网络,由可见层 (visible layer) 和隐藏层 (hidden layer) 组成,具有以下关键特性:
| 特性 | 说明 |
|---|---|
| 二分图结构 | 仅可见层与隐藏层之间存在全连接,层内无任何连接 (这是 "限制性" 的由来) |
| 随机性 | 神经元状态是随机变量 (通常为二值 {0,1},也有高斯、Softmax 等变体) |
| 生成能力 | 不仅能编码输入数据,还能从学习到的分布中采样生成新数据 |
| 无监督学习 | 无需标签即可学习数据的内在结构和特征表示 |
| 条件独立性 | 给定可见层状态,隐藏层各单元条件独立;反之亦然 |
三、网络结构详解
-
层结构
- 可见层 (v):接收输入数据,维度为输入特征数 (如图片像素数)
- 隐藏层 (h):学习输入数据的抽象特征,维度由任务决定
- 权重矩阵 (W):连接可见单元 v_i 和隐藏单元 h_j,大小为隐藏层维度 × 可见层维度
- 偏置向量:可见层偏置 b (维度 = 可见层大小),隐藏层偏置 c (维度 = 隐藏层大小)
-
图形表示
bash可见层单元: v₁ ──── W₁ⱼ ──── hⱼ ─ 隐藏层单元 v₂ ──── W₂ⱼ ──── hⱼ ... ... vₙ ──── Wₙⱼ ──── hⱼ注:层内无连接,层间全连接
四、能量函数与概率分布
RBM 的核心是基于能量函数定义的概率分布,这源自统计力学中的玻尔兹曼分布。
1. 能量函数 (Energy Function)
对于给定的可见层状态向量 v 和隐藏层状态向量 h,RBM 的能量函数定义为:
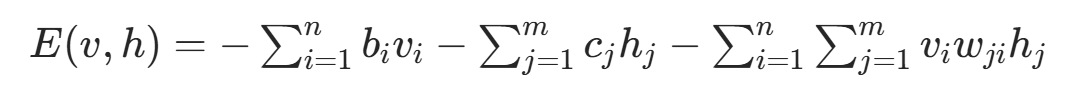
- n: 可见层单元数,m: 隐藏层单元数
: 可见单元
的偏置
: 隐藏单元
的偏置
: 连接
和
的权重
2. 联合概率分布
基于能量函数,可见层与隐藏层的联合概率分布为玻尔兹曼分布:
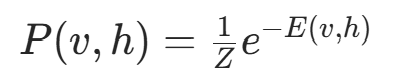
其中配分函数 (Partition Function) Z是归一化因子,确保概率和为 1:
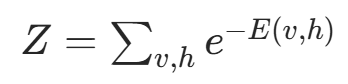
注:Z 的计算通常是 NP 难问题,这也是 RBM 训练的主要挑战之一
3. 边缘与条件概率
由于二分图结构,条件概率可高效计算:
-
隐藏层条件概率 (给定可见层 v):
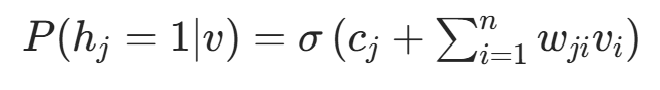
-
可见层条件概率 (给定隐藏层 h):
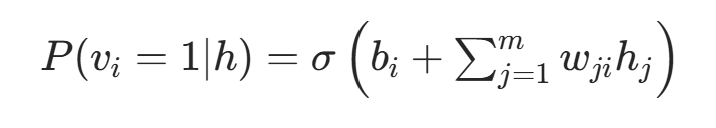
其中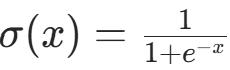 是Sigmoid 函数,确保输出在 [0,1] 区间内,可解释为神经元激活的概率。
是Sigmoid 函数,确保输出在 [0,1] 区间内,可解释为神经元激活的概率。
五、训练算法:对比散度 (Contrastive Divergence, CD)
RBM 的训练目标是最大化训练数据的对数似然 :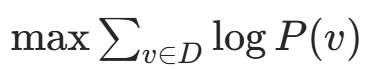 ,但直接计算梯度涉及配分函数 Z,难以处理。Hinton 提出的对比散度 (CD)算法是 RBM 训练的突破,它通过近似采样避免了直接计算 Z。
,但直接计算梯度涉及配分函数 Z,难以处理。Hinton 提出的对比散度 (CD)算法是 RBM 训练的突破,它通过近似采样避免了直接计算 Z。
CD-k 算法流程 (以 k=1 为例)
-
正向阶段 (Positive Phase)
- 输入训练样本 v₀,计算隐藏层激活概率
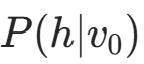
- 采样得到隐藏层状态 h₀(通常用伯努利采样)
- 计算正梯度:
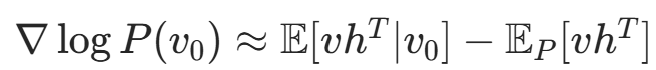 (前半部分)
(前半部分)
- 输入训练样本 v₀,计算隐藏层激活概率
-
重构阶段 (Reconstruction Phase)
- 从 h₀重构可见层 v₁:计算
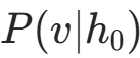 并采样
并采样 - 从 v₁计算新的隐藏层 h₁:
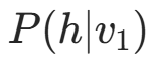 并采样
并采样 - 计算负梯度:
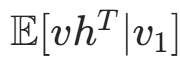 (近似后半部分
(近似后半部分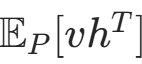 )
)
- 从 h₀重构可见层 v₁:计算
-
参数更新
- 权重更新:
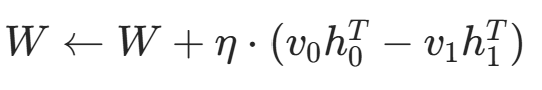
- 偏置更新:
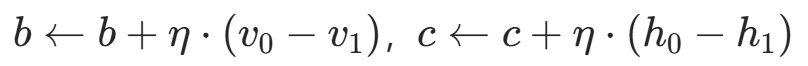
- 其中η为学习率
- 权重更新:
CD-k 的关键思想
- k=1 通常已足够好,计算效率高
- 通过吉布斯采样(Gibbs sampling) 在模型分布中生成 "幻想样本"(fantasy particles)
- 用短期马尔可夫链(short Markov chain) 近似长期平衡状态
六、RBM 的变体
为适应不同数据类型和任务,RBM 有多种变体:
| 变体 | 适用场景 | 特点 |
|---|---|---|
| 伯努利 - 伯努利 RBM | 二值数据 (如黑白图像、二进制特征) | 可见层和隐藏层均为二值单元 |
| 高斯 - 伯努利 RBM | 连续数据 (如实数像素、传感器数据) | 可见层为高斯单元,隐藏层为二值单元;能量函数中可见层项改为∑(vi−bi)2/(2σ2) |
| Softmax - 伯努利 RBM | 分类任务 (多类别标签) | 可见层为 Softmax 单元,处理离散多类别数据 |
| 深度玻尔兹曼机 (DBM) | 更复杂的特征学习 | 多个隐藏层,层间全连接,层内无连接 |
| 卷积 RBM (CRBM) | 图像等网格数据 | 权重共享,减少参数,提取局部特征 |
七、RBM 的应用领域
RBM 在机器学习和深度学习中有广泛应用,尤其在深度学习早期阶段发挥重要作用:
-
特征学习与降维
- 无监督提取数据的抽象特征,用于后续分类 / 回归任务
- 替代 PCA 等传统降维方法,能捕捉非线性关系
-
深度信念网络 (DBN) 预训练
- DBN 由多层 RBM 堆叠而成,逐层预训练后再微调
- 解决了深层网络训练的梯度消失问题,是深度学习复兴的关键技术之一
-
协同过滤与推荐系统
- Netflix Prize 竞赛中,RBM 被证明优于传统方法
- 建模用户 - 物品交互,预测用户对未评分物品的偏好
-
图像生成与重构
- 学习图像分布,生成新图像 (如手写数字)
- 图像去噪、超分辨率、修复等任务
-
自然语言处理
- 文本特征提取、主题建模
- 语言模型、机器翻译的预训练
-
强化学习
- 状态表示学习,为智能体提供更好的特征空间
八、RBM 与其他模型的关系
-
与玻尔兹曼机 (BM) 的区别
- BM:层内和层间均可有连接,计算复杂,难以训练
- RBM:层内无连接,条件独立,计算高效,可训练大规模网络
-
与自编码器 (AE) 的比较
- 相同:均为无监督特征学习,有编码 - 解码过程
- 不同:RBM 是概率模型 (生成式),AE 是确定性模型(判别式);RBM 可采样生成数据,AE 主要用于重构和降维
-
与深度学习的关系
- RBM 是深度学习早期的核心模型,推动了 DBN 的发展
- 为后续深度学习模型 (如 CNN、RNN、Transformer) 提供了无监督预训练的思路
九、优缺点分析
优点
- 强大的特征学习能力:能捕捉数据中的复杂非线性关系
- 生成能力:不仅能编码还能生成数据
- 计算效率:二分图结构使条件概率计算和采样高效
- 无监督学习:无需标签,降低数据标注成本
缺点
- 训练复杂:依赖 CD 等近似算法,参数调优 (学习率、k 值) 敏感
- 表达能力有限:单层结构难以建模非常复杂的数据分布 (需堆叠成 DBN)
- 采样质量:生成样本可能存在模式崩溃或多样性不足
- 与现代深度学习模型相比:计算效率和表达能力已被更先进的模型 (如 GAN、VAE、Transformer) 超越
十、限制性玻尔兹曼机(RBM)的Python代码完整实现
python
import numpy as np
import matplotlib.pyplot as plt
from tqdm import tqdm
# ===================== RBM类实现 =====================
class BernoulliRBM:
"""
伯努利-伯努利RBM实现(二值可见层+二值隐藏层)
核心训练算法:CD-1(对比散度,k=1)
"""
def __init__(self, n_visible, n_hidden, learning_rate=0.1, random_state=42):
"""初始化RBM参数"""
np.random.seed(random_state)
# 权重矩阵:n_hidden × n_visible,小正态分布初始化
self.W = np.random.normal(0, 0.1, (n_hidden, n_visible))
# 可见层/隐藏层偏置初始化为0
self.b = np.zeros(n_visible)
self.c = np.zeros(n_hidden)
# 超参数
self.lr = learning_rate
self.n_visible = n_visible
self.n_hidden = n_hidden
def sigmoid(self, x):
"""Sigmoid激活函数(防止数值溢出)"""
x = np.clip(x, -500, 500)
return 1 / (1 + np.exp(-x))
def sample_h_given_v(self, v):
"""给定可见层v,计算隐藏层概率并采样"""
h_prob = self.sigmoid(self.c + np.dot(v, self.W.T))
h_sample = np.random.binomial(n=1, p=h_prob)
return h_prob, h_sample
def sample_v_given_h(self, h):
"""给定隐藏层h,重构可见层并采样"""
v_prob = self.sigmoid(self.b + np.dot(h, self.W))
v_sample = np.random.binomial(n=1, p=v_prob)
return v_prob, v_sample
def train(self, X, epochs=10, batch_size=8):
"""CD-1训练核心"""
n_samples = X.shape[0]
for epoch in tqdm(range(epochs), desc="Training RBM"):
# 每轮打乱数据
idx = np.random.permutation(n_samples)
X_shuffled = X[idx]
# 批次训练
for batch_start in range(0, n_samples, batch_size):
batch_end = min(batch_start + batch_size, n_samples)
v0 = X_shuffled[batch_start:batch_end]
# 正向阶段:v0 → h0
h0_prob, h0_sample = self.sample_h_given_v(v0)
# 重构阶段:h0 → v1 → h1
v1_prob, v1_sample = self.sample_v_given_h(h0_sample)
h1_prob, _ = self.sample_h_given_v(v1_sample)
# 参数更新(CD-1核心)
pos_grad = np.dot(h0_sample.T, v0)
neg_grad = np.dot(h1_prob.T, v1_sample)
self.W += self.lr * (pos_grad - neg_grad) / batch_size
self.b += self.lr * np.mean(v0 - v1_sample, axis=0)
self.c += self.lr * np.mean(h0_sample - h1_prob, axis=0)
def generate(self, n_samples=8, n_gibbs_steps=50):
"""吉布斯采样生成新样本"""
# 随机初始化可见层
v = np.random.binomial(1, 0.5, (n_samples, self.n_visible))
# 交替采样v和h,收敛到模型分布
for _ in range(n_gibbs_steps):
_, h = self.sample_h_given_v(v)
_, v = self.sample_v_given_h(h)
return v
# ===================== 步骤1:生成人工二值数据集 =====================
def create_synthetic_data(n_samples=1000, n_visible=16):
"""
生成人工二值数据集(4x4像素=16维),包含两种核心模式:
模式1:前8个像素为1,后8个为0(左上半亮,右下半暗)
模式2:前8个像素为0,后8个为1(左下半暗,右下半亮)
加入少量噪声,模拟真实数据
"""
data = []
for _ in range(n_samples):
# 随机选模式1或模式2
if np.random.rand() < 0.5:
sample = np.array([1] * 8 + [0] * 8) # 模式1
else:
sample = np.array([0] * 8 + [1] * 8) # 模式2
# 加入5%的随机噪声(翻转部分像素)
noise = np.random.binomial(1, 0.05, n_visible)
sample = np.abs(sample - noise) # 翻转噪声位置的像素
data.append(sample)
return np.array(data)
# ===================== 步骤2:主程序 =====================
if __name__ == "__main__":
# 超参数(4x4像素=16维可见层,8维隐藏层)
n_visible = 16 # 4x4像素
n_hidden = 8
learning_rate = 0.1
epochs = 20 # 训练轮数(少量即可收敛)
batch_size = 8
# 1. 生成人工数据集
print("Generating synthetic binary data...")
X_train = create_synthetic_data(n_samples=1000, n_visible=n_visible)
# 2. 初始化并训练RBM
print("Training RBM (no external data required)...")
rbm = BernoulliRBM(n_visible=n_visible, n_hidden=n_hidden,
learning_rate=learning_rate, random_state=42)
rbm.train(X_train, epochs=epochs, batch_size=batch_size)
# 3. 生成新样本
print("Generating new samples from RBM...")
generated_samples = rbm.generate(n_samples=8, n_gibbs_steps=50)
# 4. 可视化结果(原始样本 vs 生成样本)
fig, axes = plt.subplots(2, 8, figsize=(12, 4))
# 绘制原始样本(前8个)
for i in range(8):
axes[0, i].imshow(X_train[i].reshape(4, 4), cmap='gray', vmin=0, vmax=1)
axes[0, i].axis('off')
axes[0, 0].set_title("Original Synthetic Samples", fontsize=8)
# 绘制生成样本
for i in range(8):
axes[1, i].imshow(generated_samples[i].reshape(4, 4), cmap='gray', vmin=0, vmax=1)
axes[1, i].axis('off')
axes[1, 0].set_title("Generated Samples by RBM", fontsize=8)
plt.tight_layout()
plt.show()
# 打印简单统计:验证生成样本是否符合核心模式
print("\n=== 生成样本统计(前8维均值/后8维均值)===")
for i in range(8):
sample = generated_samples[i]
mean_first8 = np.mean(sample[:8])
mean_last8 = np.mean(sample[8:])
print(f"Sample {i + 1}: 前8维均值={mean_first8:.2f}, 后8维均值={mean_last8:.2f}")十一、程序运行结果展示
Generating synthetic binary data...
Training RBM (no external data required)...
Training RBM: 100%|██████████| 20/20 [00:00<00:00, 79.62it/s]
Generating new samples from RBM...
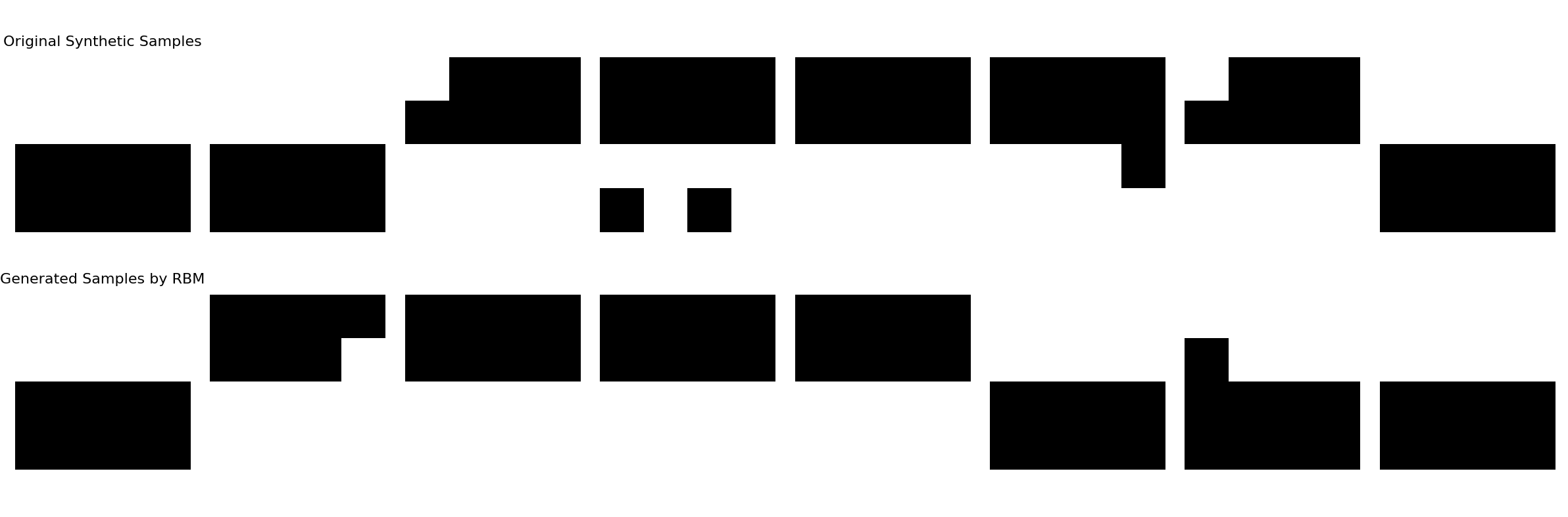
=== 生成样本统计(前8维均值/后8维均值)===
Sample 1: 前8维均值=1.00, 后8维均值=0.00
Sample 2: 前8维均值=0.12, 后8维均值=1.00
Sample 3: 前8维均值=0.00, 后8维均值=1.00
Sample 4: 前8维均值=0.00, 后8维均值=1.00
Sample 5: 前8维均值=0.00, 后8维均值=1.00
Sample 6: 前8维均值=1.00, 后8维均值=0.00
Sample 7: 前8维均值=0.88, 后8维均值=0.00
Sample 8: 前8维均值=1.00, 后8维均值=0.00
十二、总结
限制性玻尔兹曼机(RBM)是一种无监督学习的生成式神经网络模型,由可见层和隐藏层构成二分图结构,通过能量函数定义概率分布。其核心训练算法是对比散度(CD),通过近似采样避免直接计算配分函数。RBM具有多种变体,可应用于特征学习、推荐系统等领域,曾是深度学习早期重要模型。本文详细阐述了RBM的网络结构、数学原理、训练方法,并提供了Python实现代码,通过人工数据集展示了其生成能力。虽然现代深度学习中RBM已较少直接使用,但其思想对后续模型发展产生了深远影响。