(leetcode)力扣100 31K个一组翻转链表（模拟）

题目

给你链表的头节点 head ，每 k 个节点一组进行翻转，请你返回修改后的链表。

k 是一个正整数，它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。

你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。

数据范围

链表中的节点数目为 n

1 <= k <= n <= 5000

0 <= Node.val <= 1000

测试用例

示例1

java 复制代码

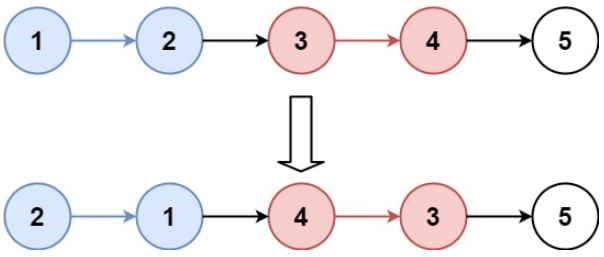
输入：head = [1,2,3,4,5], k = 2
输出：[2,1,4,3,5]

示例2

java 复制代码

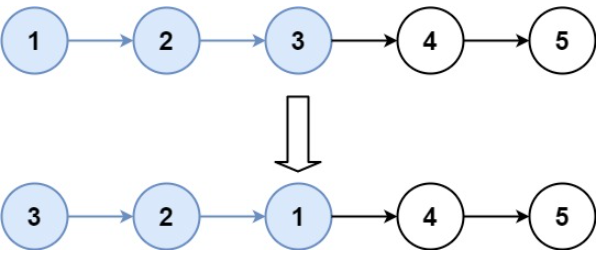
输入：head = [1,2,3,4,5], k = 3
输出：[3,2,1,4,5]

题解1（模拟，时间On空间O1，博主版本）

java 复制代码

/**
 * Definition for singly-linked list.
 * public class ListNode {
 * int val;
 * ListNode next;
 * ListNode() {}
 * ListNode(int val) { this.val = val; }
 * ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {

    /**
     * 主函数：K个一组翻转链表
     * 时间复杂度：O(N) - 每个节点大概被访问两次
     * 空间复杂度：O(1) - 只使用了有限的指针变量
     */
    public ListNode reverseKGroup(ListNode head, int k) {
        // 1. 边界条件判断：如果链表为空或只有一个节点，无需翻转直接返回
        if(head == null || head.next == null){
            return head;
        }

        // th (temp head): 当前组的头
        // tt (temp tail): 当前组的尾
        ListNode th = head;
        ListNode tt = th;

        // 2. 检查第一组是否凑够了 k 个节点
        // 如果不足 k 个，gettail 会返回 null 或 最后的节点（取决于具体实现，这里如果是 null 说明不够）
        // 但注意：你的 gettail 逻辑是如果不够 k 个，会返回 null (因为 k-- 到不了0) 或者 剩下的那个尾巴
        // 这里的逻辑主要是为了定下整个链表的新头节点 res
        tt = gettail(k - 1, tt);
        
        // res: 最终返回的结果头节点。
        // 如果第一组就够 k 个，res 就是第一组翻转后的头（也就是原来的第 k 个节点 tt）。
        // 如果不够，res 可能需要保持 head（但在你的逻辑里，如果 tt 为 null，下面的 while 不会执行，res 会是 null，这里其实有个小隐患，见下方说明）
        ListNode res = tt; 

        // 3. 主循环：只要当前组的头和尾都不为空，就开始翻转
        while(th != null && tt != null){
            // 执行翻转：将 th 到 tt 这一段翻转
            reverse(th, tt);
            
            // temp 保存下一组的开始节点
            // 此时 th 已经是当前组翻转后的尾巴了，th.next 指向的是下一组的头
            ListNode temp = th.next;

            // 关键逻辑：尝试把当前组的尾巴（th），直接连到【下一组的尾巴】
            // 因为下一组翻转后，它的尾巴会变成头。
            // 风险：如果下一组不足 k 个，gettail 返回 null，导致 th.next 被置为 null，这里造成了"断链"
            th.next = gettail(k - 1, th.next);

            // 更新指针，准备处理下一组
            if(temp == null){
                // 如果没有下一组了，但是由于上面的 th.next 可能被置为 null 了，这里其实 break 出去后需要补救
                th.next = temp; 
                break;
            } else {
                // 移动 th 和 tt 到下一组
                th = temp;
                tt = th;
                tt = gettail(k - 1, tt); // 寻找下一组的尾巴
            }
        }
        
        // 4. 补救逻辑 (Repair Loop)
        // 因为上面的循环中，当剩余节点不足 k 个时，th.next 被错误地指向了 gettail 的结果(null)
        // 所以这里需要重新遍历一次链表，找到断开的地方，把剩下的节点接回去。
        ListNode tres = res;

        // 这个循环用来找到当前已构建好链表的最后一个节点
        while(true){
            // 如果 res 本身是 null (说明第一组都不够 k 个)，或者找到了尾部
            if(tres == null) {
                // 这是一个特殊情况处理，如果第一组都不够k个，tt是null，res是null
                // 这里应该直接返回 head。
                return head; 
            }

            if(tres.next == null){
                // 找到了断开的地方，把剩下的节点 (th) 接上去
                // 注意：这里的 th 在上面循环结束时，指向的是剩余部分那一小段的头
                tres.next = th;
                break;
            }
            tres = tres.next;
        }

        return res;
    }

    /**
     * 辅助函数：翻转区间 [head, tail] 内的节点
     * 注意：这是一个左闭右闭区间的翻转
     */
    public static void reverse(ListNode head, ListNode tail){
        // temp 记录这一段之后的那个节点（下一段的头）
        ListNode temp = tail.next;
        ListNode pre = null;
        ListNode cur = head;
        
        // 标准的链表翻转逻辑
        while(cur != temp){
            ListNode next = cur.next;
            cur.next = pre;
            pre = cur;
            cur = next;
        }
        // 翻转完成后，原来的头 (head) 变成了尾，
        // 需要让它指向下一段的头 (temp)，保证链表不断开
        head.next = temp;
    }

    /**
     * 辅助函数：获取从 head 开始往后第 k 个节点（也就是当前组的尾巴）
     * 实际上是移动 k 次（传入的是 k-1，说明是移动 k-1 步找到第 k 个节点）
     */
    public static ListNode gettail(int k, ListNode head){
        while(head != null && k > 0){
            head = head.next;
            k--;
        }
        return head;
    }
}

题解2（时空同上，但是官解）

java 复制代码

class Solution {
    public ListNode reverseKGroup(ListNode head, int k) {
        ListNode hair = new ListNode(0);
        hair.next = head;
        ListNode pre = hair;

        while (head != null) {
            ListNode tail = pre;
            // 查看剩余部分长度是否大于等于 k
            for (int i = 0; i < k; ++i) {
                tail = tail.next;
                if (tail == null) {
                    return hair.next;
                }
            }
            ListNode nex = tail.next;
            ListNode[] reverse = myReverse(head, tail);
            head = reverse[0];
            tail = reverse[1];
            // 把子链表重新接回原链表
            pre.next = head;
            tail.next = nex;
            pre = tail;
            head = tail.next;
        }

        return hair.next;
    }

    public ListNode[] myReverse(ListNode head, ListNode tail) {
        ListNode prev = tail.next;
        ListNode p = head;
        while (prev != tail) {
            ListNode nex = p.next;
            p.next = prev;
            prev = p;
            p = nex;
        }
        return new ListNode[]{tail, head};
    }
}

思路

这道题虽然被标注了困难，但我觉得和前几天的简单题目没有什么区别。无非是用到了链表翻转这个我们之前做过的简单题，其他的正常模拟即可。

虽然大家的核心思路都是模拟（Simulation），但在状态管理和链表连接的策略上，官方题解确实处理得更加"老练"，主要体现在以下两点差距：

哨兵节点的妙用（Dummy Node）我在解法1中是直接操作 head，这就导致我需要一个额外的逻辑来确定最终返回的头节点（因为第一组反转后，头节点变了）。如果第一组不足 k 个，返回的又是原 head，这增加了边界判断的复杂度。而官解引入了 hair（哨兵节点），让 hair.next 指向 head。无论后续怎么翻转，最后只需要无脑返回 hair.next 即可，规避了头节点变动带来的分类讨论。
"向后预判" vs "向前连接" （核心差异）这是导致我代码中必须写一个 while(true) 修补循环的根本原因。

我的策略（向后预判）：我在处理当前组时，试图直接让当前组的尾巴去连下一组翻转后的尾巴（th.next = gettail(...)）。这就非常"激进"，因为如果下一组不足 k 个节点（不需要翻转），gettail 会返回 null，导致我的链表在中间断开了（比如 1-2-3-4-5，k=2，处理完3-4后，5被断开了）。所以我不得不在最后写一个修补循环，把断掉的节点重新接回去。

官解策略（向前连接）：官解维护了一个 pre 指针，代表"上一组的尾巴"。它只关注把当前组接在 pre 后面（pre.next = head）。这种写法是"向后兼容"的，它不需要预判下一组的情况。如果后面不足 k 个，直接 return 即可，链表本身从未断裂，自然也不需要额外的修补逻辑。

总结：虽然两种解法的时间复杂度都是 O(N)O(N)O(N)，空间复杂度都是 O(1)O(1)O(1)，但官解通过维护 pre 指针，省去了断链修复的过程，代码逻辑更加稳健简洁。