比赛链接:Dashboard - Codeforces Round 1059 (Div. 3) - Codeforces
A:

签到题,模拟即可。
代码略。
B:
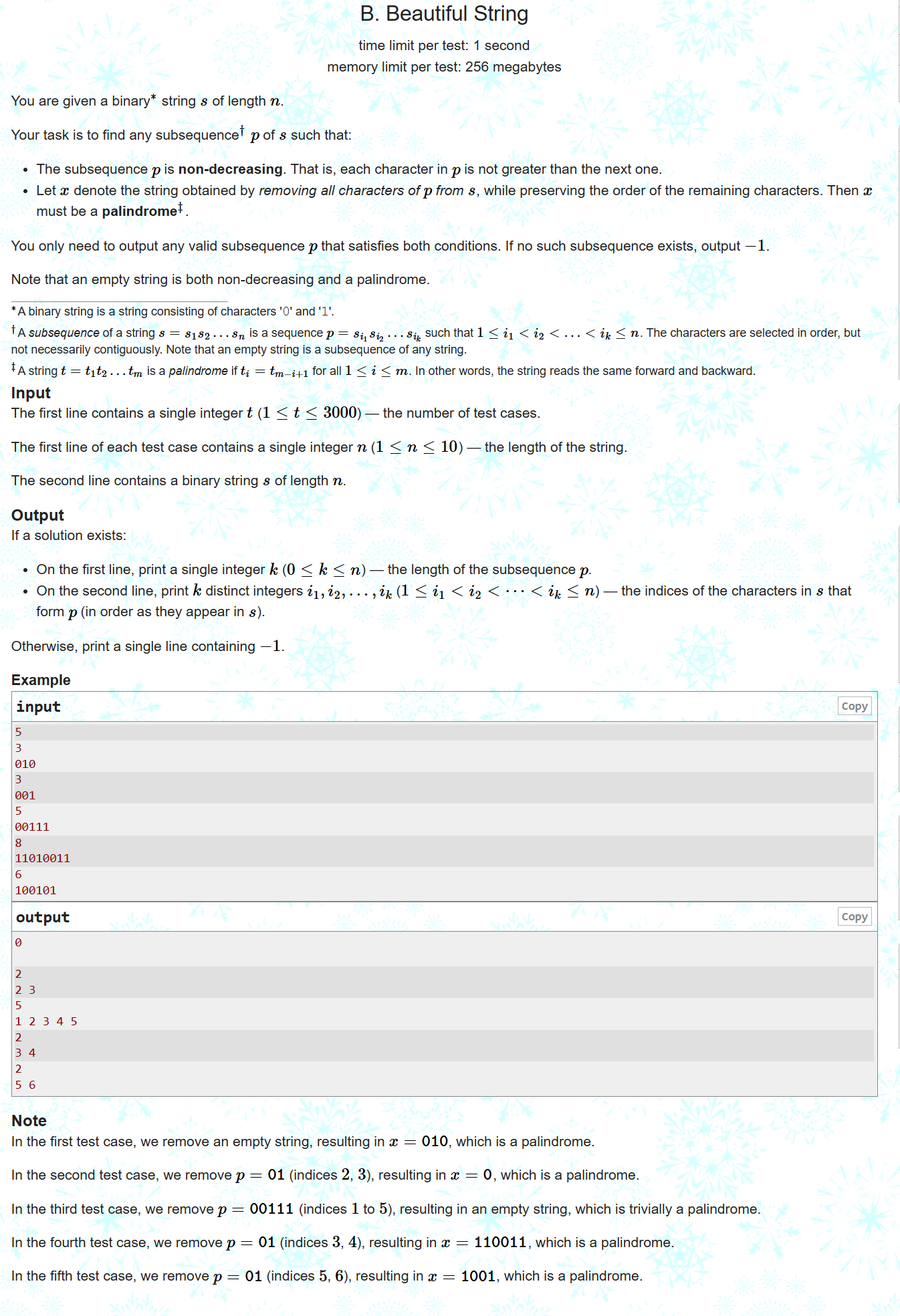
模拟枚举所有答案,看答案是否合适即可即可。
AC代码如下:
cpp
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+100;
int n;
string s;
bool check1(string a){
for(int i=1;i<a.size();i++)
if(a[i-1]=='1'&&a[i]=='0')
return false;
return true;
}
bool check2(string a){
for(int i=0,j=a.size()-1;i<=j;i++,j--)
if(a[i]!=a[j])
return false;
return true;
}
void print(int x){
if(x==-1)
cout<<-1<<'\n';
else{
int cnt=0;
for(int i=0;i<n;i++)
if(x&(1<<i))
cnt++;
cout<<cnt<<'\n';
for(int i=0;i<n;i++)
if(x&(1<<i))
cout<<i+1<<' ';
cout<<'\n';
}
}
void solve(){
cin>>n;
cin>>s;
int res=-1;
for(int i=0;i<(1<<n);i++){
string a,b;
for(int j=0;j<n;j++){
if(i&(1<<j))
a=a+s[j];
else
b=b+s[j];
}
if(check1(a)&&check2(b)){
res=i;
break;
}
}
print(res);
}
int main(){
int t;
cin>>t;
while(t--){
solve();
}
return 0;
}C:

把a、b拆分成二进制形式,有以下两个结论:
所以对于a、b而言,假设第 位不同(
从0开始),那么就让
,要确保
符合条件。
AC代码:
cpp
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+100;
int a,b;
void solve(){
cin>>a>>b;
bool r=false;
vector<int>c;
int k=0;
for(int i=0;i<=30;i++)
if(a&(1<<i)){
k=i;
}
for(int i=0;i<=30;i++){
if((a>>i)%2!=(b>>i)%2){
if(i>k)
r=true;
else
c.push_back(1<<i);
}
}
if(r)
cout<<-1<<'\n';
else{
cout<<c.size()<<'\n';
for(auto x:c)
cout<<x<<' ';
cout<<'\n';
}
}
int main(){
int t;
cin>>t;
while(t--){
solve();
}
return 0;
}D:

首先,单纯对区间 进行操作1、2的任何一种操作我感觉得不出直观的规律,必须对区间
同时进行操作1、2才行,所以我的想法基本上就是操作1、2绑起来进行。
我的想法是先 全看一遍,确定
的大小,设其为
。
然后通过二分来找到 的位置,最后答案就是
。
AC代码:
cpp
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e5+100;
ll op(int x,int l,int r){
cout<<x<<' '<<l<<' '<<r<<'\n';
ll y;
cin>>y;
return y;
}
int n;
void print(int l,int r){
cout<<"! "<<l<<' '<<r<<'\n';
}
int len;
void solve(){
cin>>n;
ll x=op(1,1,n);
ll y=op(2,1,n);
len=y-x;
int l=1,r=n,ans=-1;
while(l<=r){
int mid=(l+r)/2;
x=op(1,l,mid);
y=op(2,l,mid);
if(x==y){
l=mid+1;
}else{
r=mid-1;
ans=mid;
}
}
print(ans,ans+len-1);
}
int main(){
int t;
cin>>t;
while(t--){
solve();
}
return 0;
}E:

这道题我感觉有很多种思路,先分享一下我自己的,虽然没有题解好。
假设两个不同的数前后规定为一个组,对于 这样的组合,长度为
的数组最多只有
种不同的组。
而要想组成一个回文字符串,那么最基本得满足以下形式:
,也就是回文串最前面的两个字符和最后面的两个字符各形成的组必须是对称的。
而 个数又可以构成
种不同的组合,假设
是最坏的情况,那么我们最多有
种不同的组。
而又由于 对于
都成立,所以理论上我们大多数情况都可以填满,除了,以下这种情况:
,且数组为
的形式,这种情况就特判处理一下(因为这种情况正好无法填充),剩余情况就按照上述方法填充。
那么如何填充呢?
我们肯定就是在当前数组的末尾填充,因此,我们不妨维护 每个数
对应的
,满足
在当前数组没有出现过,且记录
每个数
在当前数组组成
形式的
出现次数。
对于当前数组的末尾 ,我们要找到一个数
,满足以下要求:
、
这种组合在当前数组没有出现过。
、在当前数组中,以
打头,且形成
这种不同的组合数小于
。
满足以上要求后,才能把 放到当前数组最后面。
(以上感觉看看就好,赛后感觉又麻烦时间复杂度又比较差)
AC代码:
cpp
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int,int> PII;
const int N=5e5+100;
int n,k;
int a[N],cun[N],cnt[N];
void solve(){
cin>>n>>k;
map<PII,bool>st;
for(int i=1;i<=n;i++){
cin>>a[i];
cun[i]=1;
st[{i,i}]=true;
cnt[i]=1;
}
if(n==3&&a[1]==a[3]&&a[1]!=a[2]&&k==3){
cout<<6-a[1]-a[2]<<' '<<a[2]<<' '<<a[1]<<'\n';
return ;
}
cun[1]=2;
for(int i=n;i>1;i--){
st[{a[i],a[i-1]}]=true;
cnt[a[i]]++;
}
vector<int>res;
while(k--){
while(st[{a[n],cun[a[n]]}]||cnt[cun[a[n]]]>=n)
cun[a[n]]++;
res.push_back(cun[a[n]]);
int x=cun[a[n]];
st[{x,a[n]}]=true;
cnt[x]++;
a[++n]=x;
}
for(auto c:res)
cout<<c<<' ';
cout<<'\n';
}
int main(){
int t;
cin>>t;
while(t--){
solve();
}
return 0;
}还有一个更好一点的思路,就是CF题解的思路,这里就不照搬了,CF题解链接:Codeforces Round 1059 (Div. 3) Editorial - Codeforces
后续内容等考完软件构造再补充