1、DQN
用神经网络代替Q表格
用经验回放稳定训练
用目标网络防止震荡
问题1:状态太多,Q表格爆炸。
解决方案:不用表格,用神经网络拟合Q函数。
输入:当前画面(像素)
输出:每个动作的Q值(比如左=1.2,右=0.8,开火=2.5)
经验回放:把智能体玩过的经历存进一个大仓库,训练时随机抽样,打破数据相关性,稳定学习。
经验回放的定义:

【目标网络】
DQN有两个结构相同的神经网络:
主网络(Online Network):参数θ,用于选择动作和计算当前Q值
目标网络(Target Network):参数θ-,只用于计算TD目标,不参与梯度更新
目标网络更新很慢,每隔C步(比如1000步)才把主网络参数复制过去:
θ → θ-
为什么需要目标网络,自举(bootstrapping)问题。
Q-learning的更新目标是:
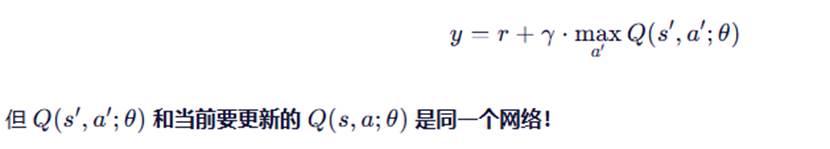
目标网络如何解决?
用固定的目标网络计算y:

学开车的举例:
经验回放:把每次练车录像存下来,回家随机看片段复盘
目标网络:教练说"本周目标:平稳起步",你按这个目标练,而不是每秒改目标。
【主网络和目标网络的区别】
主网络:负责当前怎么玩,当前认为值多少分。参与动作选择和参数更新。
目标网路:只负责告诉主网络未来理想能得多少分。仅用于计算目标值,不更新参数。
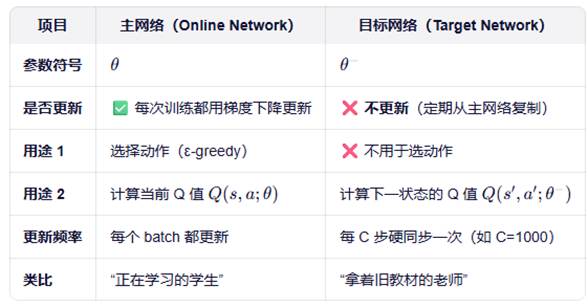
DQN的核心是最小化TD误差的平方损失:

2、价值方法/策略梯度方法
价值方法:先学每隔状态/动作值多少分,再选最高分的动作。比如:先查地图(Q表),再决定走哪条路。
策略梯度方法:直接学在什么状态下该做什么动作。好比:直接训练一个本能反应的智能体。
- 价值方法

优点:
-理论成熟,收敛性有保证
-DQN能处理高维输入(如图像)
-off-policy版本(如Q-learning)可复用任意数据
缺点:
-只能处理离散动作空间,因为要取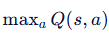
-策略是间接的,无法输出概率分布
-在连续动作空间中,max操作难以计算
- 策略梯度方法


3、策略梯度定理
我们的目标:训练一个智能体,让它在环境中获得尽可能多的总奖励。
它的行为由一个带参数 θ 的策略 π(a|s;θ) 决定。比如:在状态 s(如"球在左边"),以概率 π(左|s;θ)=0.8 按左键。
我们的目标函数是:

如何调整 θ,让 J(θ) 变大?

但问题是:J(θ) 无法直接求导。
核心思想:用对数导数技巧绕过难题。

策略梯度 = 在很多局游戏中,对每一步:
("如何调整参数才能更常选这个动作") × ("选了这个动作后总共得了多少分")
然后求平均。

问题:方差太大。G_t是整局回报,受后面很多随机因素影响。即使某步动作很好,也可能因为后面运气差导致G_t很小。
改进:引入Critic价值函数。

目的:不要只看总得分,要看这个动作比平常做得好还是差。
引入两个价值函数:

4、Actor-Critic算法
1)用TD误差来替代A(s,a)
为什么可以替代:

2)学习流程
第1步,初始化

第2步,与环境交互,收集一步经验

第3步,Critic进行评估,计算TD误差

第4步,更新Critic,让它预测更准

第5步,更新Actor,根据Critic的反馈调整策略
Actor 的目标是:多做那些被 Critic 认可的动作,少做被否定的动作。

第6步,进入下一步或新episode

重要优势:
-Actor-Critic不需要等一整局结束就能学习
-每走一步,就可以更新一次,样本效率高、学习快。
终极总结(5步口诀)

5、策略梯度到Actor-critic的演进
