
UKF融合INS与DVL的核心程序,二维
原创程序,请勿翻卖
文章目录
程序简介
代码实现了基于无迹卡尔曼滤波(UKF) 的惯性导航系统(INS)与多普勒速度计(DVL) 融合,主要用于二维速度的估计与轨迹跟踪。代码的核心流程包括初始化、滤波模型设定、运动模型生成、UKF核心算法实现以及结果的可视化。具体介绍如下:
- 滤波模型初始化
- 初始化了时间向量
t,并设置了过程噪声Q和观测噪声R。 w和v是过程噪声和观测噪声的随机分布,模拟系统中的不确定性。- 初始状态
X和滤波后的状态X_ukf被设置为零,观测值Z初始为基于速度的观测。
- 运动模型
- 代码定义了一个简单的非线性运动模型,描述了系统在二维平面内的运动(速度和位置的变化)。通过迭代方式,生成了真实的运动轨迹和带噪声的观测值。
- 真实速度和未滤波的速度模型分别计算,并将噪声加到观测值上,以便用于后续滤波处理。
- UKF参数初始化
- UKF的超参数如
alpha、beta、kappa和lambda被设置,并计算出权重系数Wm和Wc。这些参数决定了生成sigma点的分布,以及在预测和更新步骤中如何加权。
- UKF核心算法
- 生成sigma点:使用Cholesky分解生成sigma点,并对其进行扩展和缩放。这些sigma点代表了状态的不同可能值,反映了系统的不确定性。
- 预测步骤:根据运动模型预测系统的下一个状态,使用生成的sigma点计算状态均值和协方差。
- 更新步骤:根据观测值和预测值,更新系统的状态。计算预测观测值、观测协方差和互协方差,用于计算卡尔曼增益并更新滤波后的状态。
- 结果输出
- 通过多次迭代,最终输出滤波后的速度估计和轨迹估计。代码绘制了真实速度、滤波速度与未滤波速度的对比图,并计算了速度误差。
- 输出了速度误差的最大值和误差的轨迹对比,提供了对滤波精度的定量评估。
- 可视化结果
- 绘制了速度和位置的图形,比较了真实值、未滤波值和滤波后的值,便于直观地评估滤波效果。
- 通过误差图、误差统计特性计算、输出等,展示UKF滤波前后速度估计的误差对比。
- 总结
- 该代码的目的是使用UKF来处理不确定性较大的惯性导航数据,融合DVL提供的速度信息。通过滤波,能够显著提高系统在动态环境中的定位精度。
运行结果
轨迹对比:
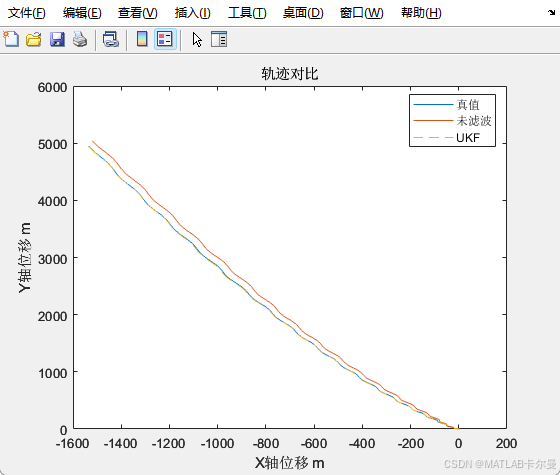
速度估计曲线:
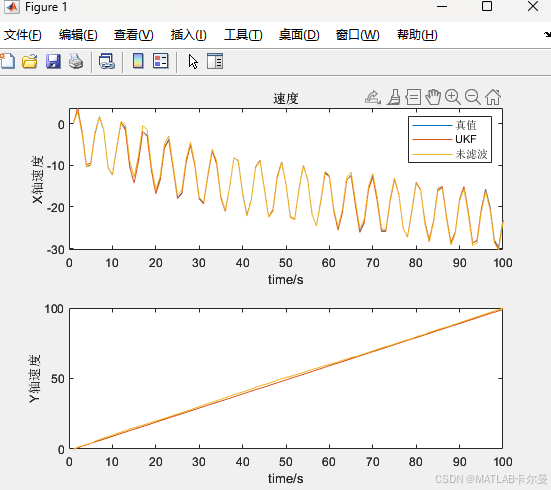
速度误差曲线:
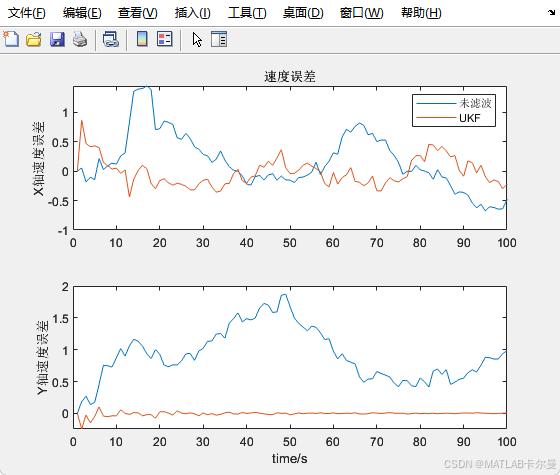
滤波前后的误差对大值对比:
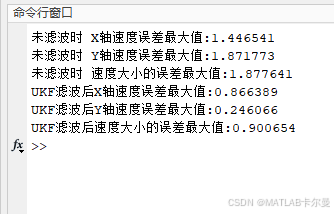
MATLAB源代码
部分代码如下:
matlab
% UKF融合INS与DVL的核心程序,二维
% 作者:matlabfilter(V同号,可接代码定制、讲解与调试)
% 2026-01-01/Ver1
clear;clc;close all;
rng(0); %注释此行可以在每次运行时使用不同的随机数
%% 滤波模型初始化
t = 1:1:100;
Q = 0.01*diag([1,1]);w=sqrt(Q)*randn(size(Q,1),length(t));
R = 1^2*diag([1,1]);v=sqrt(R)*randn(size(R,1),length(t));
P0 = 1*eye(2);
X=zeros(2,length(t)); %构建滤波状态量(二维速度)
X_ukf=zeros(2,length(t)); %构建滤波后的输出状态
X_ukf(1,1)=X(1,1);
Z=zeros(2,length(t)); %定义观测值形式
Z(:,1)=[X(1,1);X(2,1).^2]+v(:,1); %观测量------对二维速度进行观测
%% 运动模型
X_=zeros(2,length(t));
X_(:,1)=X(:,1);
for i1 = 2:length(t)
X(:,i1) = [X(1,i1-1) + (2.5 * X(1,i1-1) / (1 + X(1,i1-1).^2)) + 8 * cos(1.2*(i1-1));
X(2,i1-1)+1]; %真实值
X_(:,i1) = [X_(1,i1-1) + (2.5 * X_(1,i1-1) / (1 + X_(1,i1-1).^2)) + 8 * cos(1.2*(i1-1));
X_(2,i1-1)+1] + w(:,i1-1);%未滤波的值
Z(:,i1) = [X(1,i1);X(2,i1).^2] + v(:,i1); %观测值
end
%% UKF参数初始化
n = 2; %状态维度完整代码:https://download.csdn.net/download/callmeup/92523728
或:
如需帮助,或有导航、定位滤波相关的代码定制需求,请点击下方卡片联系作者