最小二乘 (Ordinary Least Squares, OLS) 线性回归

什么是最小二乘（OLS）线性回归？

想象一下，你想预测房价：根据房子的面积来估算价格。你收集了一些数据，比如不同面积的房子和它们的实际售价。这些数据点在图上看起来像是一堆散点。如果你能画一条直线，让它尽可能"贴近"这些点，这条线就能帮你预测新房子的价格。这就是线性回归的基本想法。

线性回归是一种统计方法，用于找到变量之间的线性关系。具体来说，普通最小二乘法（Ordinary Least Squares, OLS） 是最常见的线性回归方法。它假设因变量（比如房价）和自变量（比如面积）之间是直线关系，用公式表示为：

其中：

• y 是因变量（要预测的东西）。
• x 是自变量（已知的东西）。
• 是截距（直线与y轴的交点）。
• 是斜率（直线陡峭程度）。
• ϵ 是误差项（现实中的随机波动）。

OLS的目标是找到最佳的 β0​ 和 β1​，让预测值和实际值之间的差距最小。

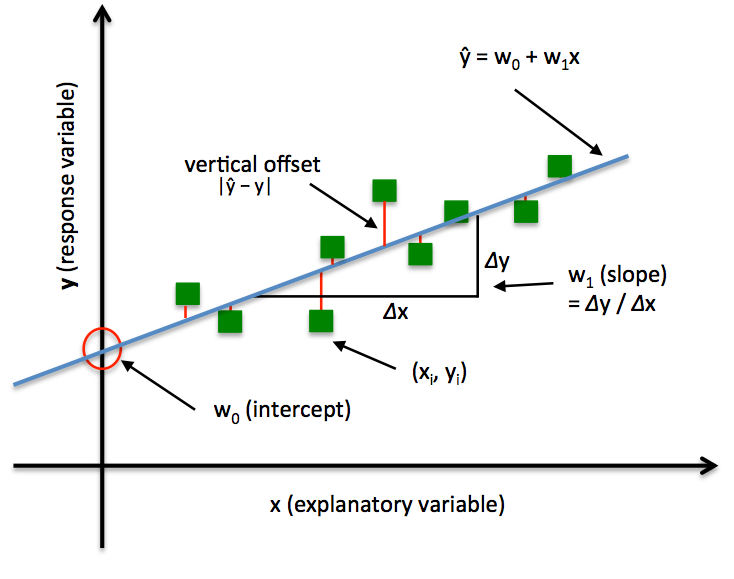
OLS 如何工作？通俗解释

OLS 的核心是"最小二乘"：它最小化所有数据点到拟合直线的垂直距离（残差）的平方和。为什么平方？因为正负残差会抵消，用平方确保都是正的，而且强调大的误差（大残差平方后更大）。

打个比方：你扔飞镖，想击中靶心。每个飞镖偏离靶心的距离就是残差。OLS 就像调整你的瞄准方式，让所有飞镖偏离距离的平方总和最小。这样，你的"平均瞄准"就最准了。

步骤简单：

1. 收集数据（x 和 y 的配对）。
2. 计算残差：对于每个点，残差 = 实际 y - 预测 y。
3. 求残差平方和（Sum of Squared Errors, SSE）。
4. 调整 β0和 β1，直到 SSE 最小。

数学上，最优参数的公式是：

（n 是数据点数， 和 ​ 是平均值）。

其中：

• n 是数据点数量（这里 n = 5）。
• 是所有 x 的总和。
• 是所有 y 的总和。
• 是每个 * 的总和。
• 是每个 平方后的总和。

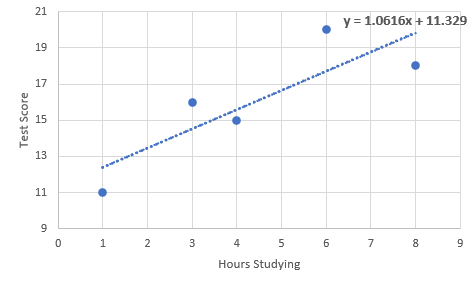
一个简单例子

假设你有5个数据点：房子面积（x，单位：平方米）和价格（y，单位：万元）。

• (50, 100), (60, 120), (70, 135), (80, 160), (90, 170)

用 OLS 计算：

• 平均 x = 70，平均 y = 137。
• 通过公式，（每多1平方米，价格涨2万元），。
• 拟合线：y = -3 + 2x。

对于一个100平方米的房子，预测价格：-3 + 2*100 = 197万元。

步骤 1: 计算基本和值

• = 50 + 60 + 70 + 80 + 90 = 350
• = 100 + 120 + 135 + 160 + 170 = 685
• = (50×100) + (60×120) + (70×135) + (80×160) + (90×170) = 5000 + 7200 + 9450 + 12800 + 15300 = 49750
• = (50²) + (60²) + (70²) + (80²) + (90²) = 2500 + 3600 + 4900 + 6400 + 8100 = 25500

步骤 2: 计算分子（numerator）

分子 = n × ∑(x_i y_i) - (∑x_i) × (∑y_i) = 5 × 49750 - 350 × 685 = 248750 - 239750 = 9000

步骤 3: 计算分母（denominator）

分母 = n × - ()² = 5 × 25500 - (350)² = 127500 - 122500 = 5000

步骤 4: 计算 β₁

β₁ = 分子 / 分母 = 9000 / 5000 = 1.8

因此，精确的 β₁ = 1.8（每增加 1 平方米，价格预计增加 1.8 万元）。之前的 ≈2 是近似值，用于简化说明，但实际计算如上。

如果数据有噪声，OLS 还能处理，但前提是数据满足线性、无多重共线性等假设（否则用其他变体）。

图片里在讲 OLS（Ordinary Least Squares，普通最小二乘）线性回归：给定一组自变量 X（解释变量）去解释/预测因变量 Y，假设它们满足"线性模型"，然后通过"让预测误差的平方和最小"来求参数 β。

---

1) 模型在说什么（对应图里的公式）

对第 n 条样本（），有 k 个解释变量：

• ：第 n 条样本的因变量

• ：第 n 条样本第 i个自变量

• ：需要估计的系数（​ 通常是截距，对应 ）

• ：误差项（模型没解释掉的部分）

图里的小散点图就是"数据点 + 一条回归线"，竖直方向的差（点到线的距离）就是残差/预测误差。

---

2) OLS 的核心原则：最小化残差平方和

对每个样本的预测值：

​

残差：

OLS 选择 β 使下面这个目标函数最小：

为什么要"平方"？

• 让正负误差不互相抵消

• 大误差惩罚更重

• 数学上可导、好求解（还能得到闭式解）

---

3) 矩阵形式（把步骤写得更清楚）

把数据堆起来：

• 设计矩阵 （第一列全 1 表示截距）

• 系数向量

• 观测向量

模型：

目标：

对目标函数求导并令其为 0，会得到正规方程：

若 可逆，则闭式解为：

几何直觉：​ 是把 y 投影 到 X 的列空间上；残差 ​ 与列空间正交（所以也与每个自变量方向"无关"）。

---

4) OLS 的标准步骤（你可以按这个流程实现）

1. 准备数据 ：收集 y 和自变量 ​（必要时做标准化/缺失值处理）。

2. 构建设计矩阵 X：第一列加 1（截距），其余列放各个特征。

3. 求系数 ​：

   • 理论公式：

   • 实际工程里常用数值更稳定的 QR 分解 / SVD 来解（避免直接求逆）。

4. 得到预测与残差 ：，​。

5. 评估拟合好坏：

   • 残差平方和 ​

   • ​

   • 估计噪声方差：​

6. 统计推断（可选但常用） ：用 得到系数标准误、t 检验、置信区间。

7. 诊断与改进 ：看残差图、异常点、共线性（ 近奇异）、必要时做特征变换或改用岭回归/套索等。

---

5) OLS 常见"成立条件"（为什么它靠谱）

典型的线性回归假设（尤其是用于推断/置信区间时）：

• 线性 ：

• 误差均值为 0 ：

• 同方差 ：

• 不相关/独立（时间序列里经常会违背）

• 进一步若假设误差正态：可得到更标准的 t/F 检验结论

我用一个一元线性回归（最直观）把 OLS 从数据到结果完整走一遍，和你图里的"点 → 回归线 → 预测误差"一一对应。

---

示例数据（5 个点）

n	x	y
1	1	2
2	2	3
3	3	5
4	4	4
5	5	6

我们要拟合一条直线：

---

Step 1：写出 OLS 的目标（最小二乘）

每个点的残差（竖直距离）：

​

OLS 让残差平方和最小：

---

Step 2：计算需要的汇总量

N=5

---

Step 3：求解系数（闭式解）

一元线性回归的 OLS 解可以写成：

​

代入数字：

• 分子：

• 分母：

所以：

再算截距：

最终回归线：

​

---

截距 β0​ 这一步，其实有如下"更容易看懂"的推法。

A) 用"均值点在回归线上"的性质（最直观）

对一元线性回归：

OLS 解有个非常重要的性质：

意思是：回归线一定穿过数据的"中心点" 。

所以截距就是把这句话变形：

​

把数字代进去（你这组数据）

• x：1,2,3,4,5

  

• y：2,3,5,4,6

  

• 我们刚算出

代入：

所以：

你可以把它理解为：

斜率 β1 决定"倾斜程度"，一旦倾斜定了，整条线还可以上下平移；OLS 选的那条线必须穿过均值点，于是平移量（截距）就被钉死了。

Step 4：算预测值、残差、平方残差（对应图里的"Error of prediction"）

x	y		残差
1	2	2.2	-0.2	0.04
2	3	3.1	-0.1	0.01
3	5	4.0	1.0	1.00
4	4	4.9	-0.9	0.81
5	6	5.8	0.2	0.04

这就是 OLS 真正在"最小化"的东西。

---

Step 5：简单评估拟合好坏（可选但常用）

总离差平方和：

决定系数：

解释：这条线大约解释了 81% 的 y 波动。

Python 代码演示：最小二乘（OLS）线性回归

下面是一个简单的 Python 代码示例，使用 scikit-learn 库来实现 OLS 线性回归。我们以之前的房子面积（x）和价格（y）数据为例：(50, 100), (60, 120), (70, 135), (80, 160), (90, 170)。代码会拟合模型、计算参数、进行预测，并绘制散点图和拟合线（不过在文本中无法直接显示图表，我会提供描述和参考图像）。

代码示例

Python

import numpy as np
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt

# 样本数据：房子面积 (x) 和价格 (y)
X = np.array([[50], [60], [70], [80], [90]])  # 面积（平方米）
y = np.array([100, 120, 135, 160, 170])  # 价格（万元）

# 创建并拟合模型
model = LinearRegression()
model.fit(X, y)

# 获取参数
beta_0 = model.intercept_
beta_1 = model.coef_[0]

# 预测一个新面积，比如 100 平方米
new_size = np.array([[100]])
predicted_price = model.predict(new_size)

# 打印结果
print(f"截距 (beta_0): {beta_0}")
print(f"斜率 (beta_1): {beta_1}")
print(f"100 平方米房子的预测价格: {predicted_price[0]}")

# 可视化（绘制散点图和拟合线）
plt.scatter(X, y, color='blue', label='实际数据')
plt.plot(X, model.predict(X), color='red', label='拟合线')
plt.xlabel('房子面积 (平方米)')
plt.ylabel('房价 (万元)')
plt.title('OLS 线性回归示例')
plt.legend()
plt.show()

运行结果

运行以上代码（不包括绘图部分）的输出为：

text

截距 (beta_0): 10.999999999999972
斜率 (beta_1): 1.8000000000000005
100 平方米房子的预测价格: 191.00000000000003

这与我们手动计算的结果一致（约 beta_0 = 11, beta_1 = 1.8）。预测值接近 191 万元。

可视化解释

代码中的 plt 部分会生成一个散点图（蓝色点代表实际数据）和一条红色拟合直线，展示 OLS 如何最小化残差。以下是类似的可视化示例（基于 Python 代码生成的 OLS 回归图）：

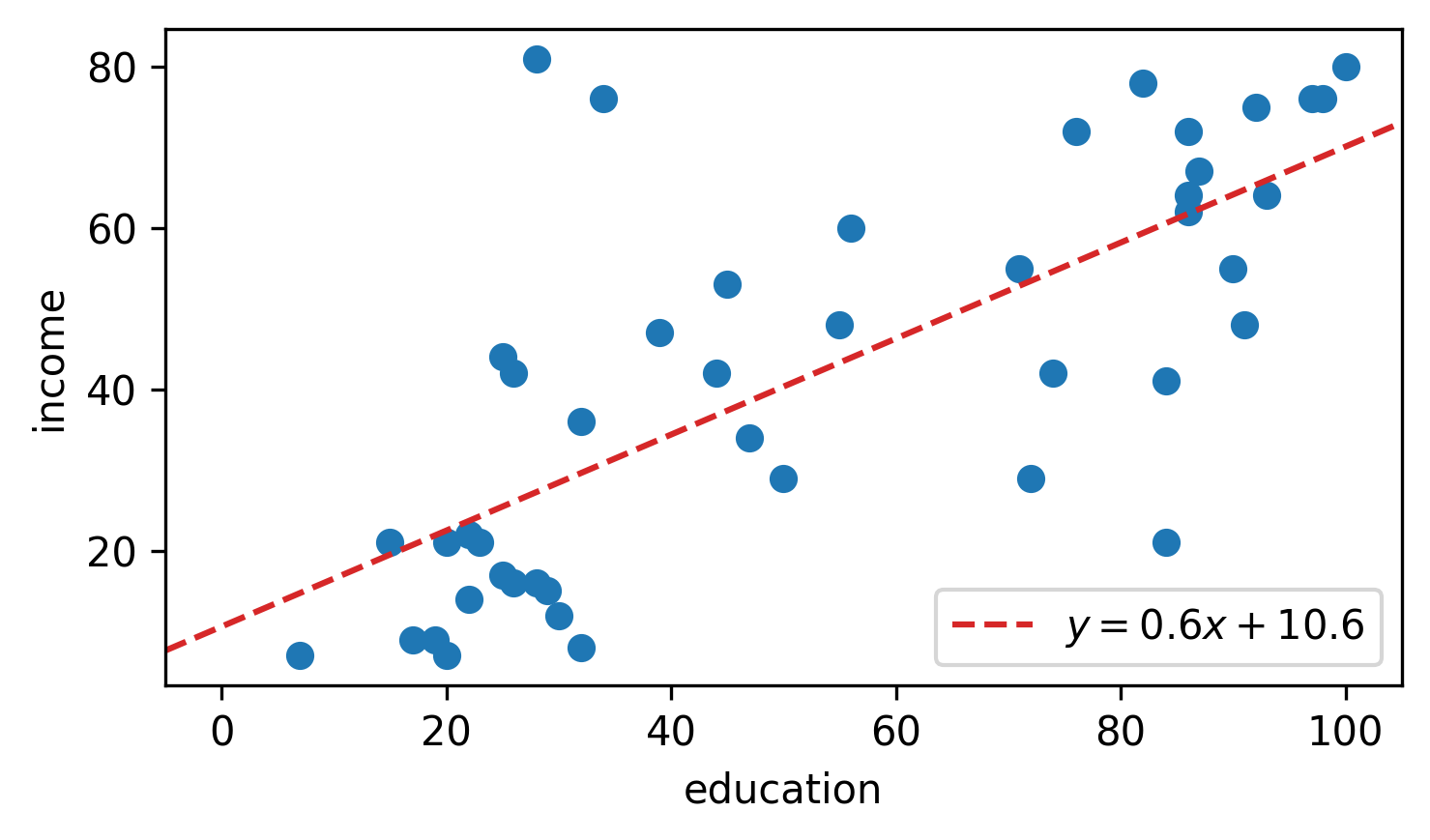
另一个示例，显示了更多数据点的拟合：

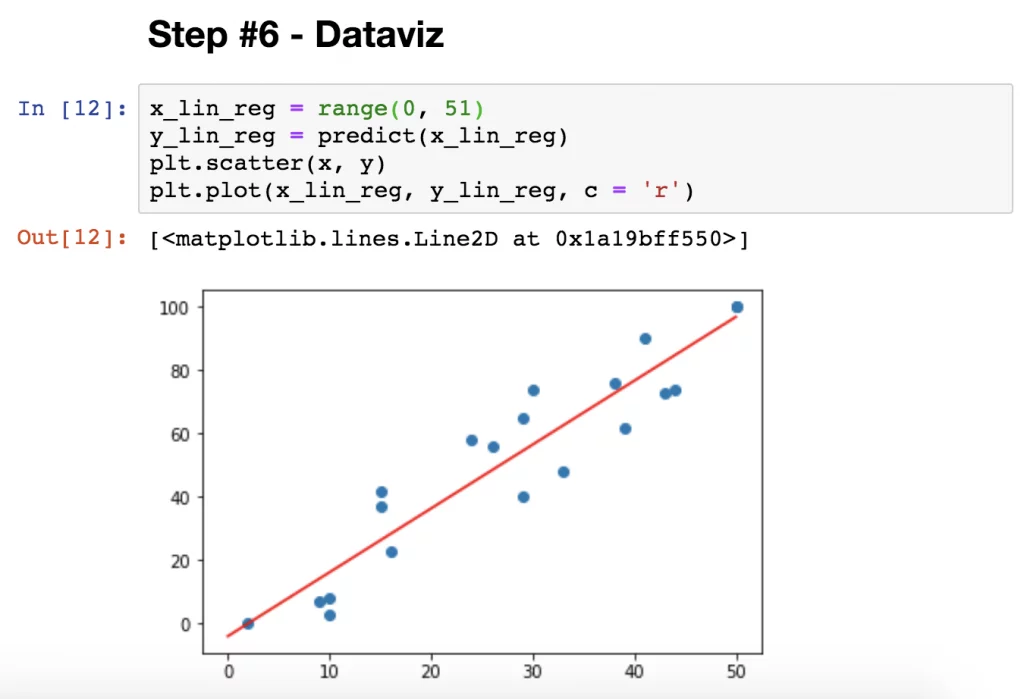
以及一个简单叠加拟合线的散点图：

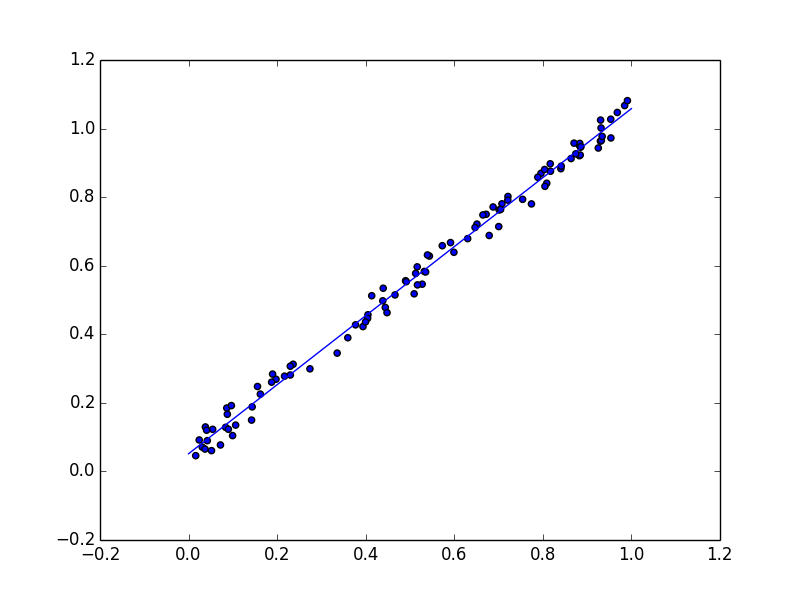
优点和局限

优点：简单、解释性强、计算快。广泛用于经济学、医学等。 局限：假设线性关系，如果数据是曲线，就不准了；对异常值敏感。

总之，OLS 就像用直尺在散点上画最佳直线，帮助我们从数据中找出规律。