Leetcode-240 :搜索二维矩阵

文章目录

[1. 题目描述](#1. 题目描述)
[2. 解题思路](#2. 解题思路)
- [2.1 dfs 或 bfs](#2.1 dfs 或 bfs)
- [2.2 暴力遍历](#2.2 暴力遍历)
- [2.3 二分优化](#2.3 二分优化)
- [2.4 Z字形查找](#2.4 Z字形查找)

1. 题目描述

原题链接

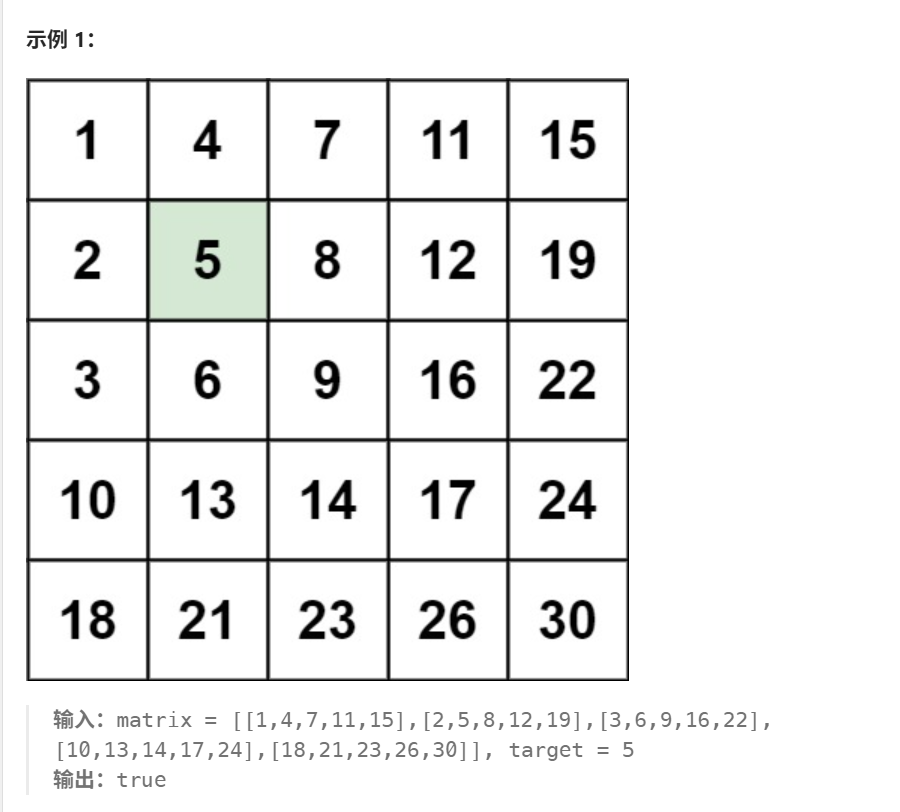
2. 解题思路

2.1 dfs 或 bfs

这道题本质就是一道搜索题，搜索可以使用dfs或bfs来做，在搜索时，利用题目中给出的已有规律，可以进一步简化dfs或bfs的搜索。

但此题用dfs或bfs会超时，因为dfs或bfs最差情况下时间复杂度会趋近于O(n ^ 2)，不过仍提供相应代码思路。

DFS :

cpp 复制代码

class Solution {
public:
    int m,n;
    bool vis[310][310] = {0};
    int dx[2] = {0,1};
    int dy[2] = {1,0};
    
    bool dfs(vector<vector<int>>& matrix,int i,int j,int target) {
        // dfs
        if(matrix[i][j] == target)
            return true;
        vis[i][j] = true;
        for(int k = 0;k < 2;k++) {
            int a = i + dx[k],b = j + dy[k];
            if(a < m && b < n && !vis[a][b] && matrix[a][b] <= target) {
                if(dfs(matrix,a,b,target))
                    return true;
            }
        }
        return false;
    }
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        m = matrix.size(),n = matrix[0].size();
        memset(vis,0,sizeof(vis));
        return dfs(matrix,0,0,target);
    }
};

BFS :

cpp 复制代码

class Solution {
public:
    int m,n;
    bool vis[310][310] = {0};
    int dx[2] = {0,1};
    int dy[2] = {1,0};
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        // bfs
        using pii = pair<int,int>;
        m = matrix.size(),n = matrix[0].size();
        memset(vis,0,sizeof(vis));
        queue<pii> q;
        q.push({0,0});
        vis[0][0] = true;
        while(!q.empty()) {
            auto [x,y] = q.front();
            q.pop();
            if(matrix[x][y] == target)
                return true;
            for(int k = 0;k < 2;k++) {
                int a = x + dx[k],b = y + dy[k];
                if(a < m && b < n && !vis[a][b] && matrix[a][b] <= target) {
                    vis[a][b] = true;
                    q.push({a,b});
                }
            }          
        }
        return false;
    }
};

2.2 暴力遍历

二维矩阵搜索目标值，另一种暴力做法就是暴力遍历，最差时间复杂度也在O(n ^ 2)。
不过暴力遍历在Leetcode上可以通过，可能因为暴力遍历是原地遍历，没有其它额外开销。

代码如下：

cpp 复制代码

class Solution {
public:
	bool searchMatrix(vector<vector<int>>& matrix,int target) {
		int m = matrix.size(),n = matrix[0].size();
		for(int i = 0; i < m; i++) {
			for(int j = 0; j < n; j++)
				if(matrix[i][j] == target)
					return true;
		}
		return false;
	}
};

2.3 二分优化

该二维矩阵每行的元素从左到右升序排列，是有序的，可以在行查找时，引入二分查找作为优化，这样可以将时间复杂度优化到O(m * LogN)。

代码如下：

cpp 复制代码

class Solution {
public:
    bool bs(vector<int>& v,int target) {
        int l = 0,r = v.size() - 1;
        while(l < r) {
            int mid = (l + r) >> 1;
            if(v[mid] >= target)
                r = mid;
            else
                l = mid + 1;
        }
        return v[l] == target;
    }
    bool searchMatrix(vector<vector<int>>& matrix, int target) 
        for(int i = 0;i < matrix.size();i++) {
            if(bs(matrix[i],target))
                return true;                     
        }
        return false;
    }
};

2.4 Z字形查找

题中二维矩阵行列均为升序排列，要充分利用行列性质，可以从最右上角的元素开始查找。
对于最右上角的元素而言，同行元素均小于该元素，同列元素均大于该元素。

那么，可进行如下分类：

target == 当前右上角元素。 此时直接返回true即可。
target < 当前右上角元素。 此时该右上角元素所在列元素均可排除，下次搜索，从原矩阵排除该列后的最右上角元素开始查找。
target > 当前右上角元素。 此时右上角元素所在行元素均可排除，下次搜索，从原矩阵排除该行后的最右上角元素开始查找。

上述查找过程，直至超出原二维矩阵边界后停止。因整个查找过程，右上角元素的移动路径，形如Z ，故称之为Z字形查找。

代码如下：

cpp 复制代码

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int m = matrix.size(),n = matrix[0].size();
        int x = 0,y = n - 1;
        while(x < m && y >= 0) {
            if(matrix[x][y] == target)
                return true;
            else if(matrix[x][y] < target)
                x++;
            else
                y--;
        }
        return false;
    }
};