DeepSeek开年王炸:mHC架构------用流形约束重构残差连接的革命性突破
论文标题 :mHC: Manifold-Constrained Hyper-Connections
作者团队 :DeepSeek-AI(Zhenda Xie等19位研究者,CEO梁文锋亲自署名)
发布时间 :2025年12月31日
论文链接:https://arxiv.org/abs/2512.24880
引言:当字节的创意遇上DeepSeek的数学洁癖
2025年的最后一天,当大家还沉浸在新年的喜悦中时,DeepSeek团队悄然在arXiv上发布了一篇硬核论文------《mHC: Manifold-Constrained Hyper-Connections》。这篇论文提出了一种名为**流形约束超连接(mHC)**的新型网络架构,被业界称为"地狱级工程难度"的创新工作。
值得注意的是,这篇论文的作者列表最后一位赫然写着:Wenfeng Liang(梁文锋)------DeepSeek的CEO亲自下场参与研究,足见这项工作的重要性。
一句话理解mHC
想象一下,神经网络就像一个复杂的水管系统,信息(水流)需要从输入端流向输出端。残差连接就像是在水管旁边加了一根"旁路管道",让水流可以绕过某些复杂的处理单元直接流过去,防止水流在复杂管道中"消失"。
**超连接(HC)**的想法是:既然一根旁路管道好用,那我们多加几根不是更好吗?于是把单车道变成了四车道。但问题来了------车道多了,交通反而乱了,经常出现"堵车"甚至"车祸"(训练崩溃)。
mHC的解决方案:给这些车道加上"智能红绿灯系统"(流形约束),让车流既能高效通行,又不会失控。
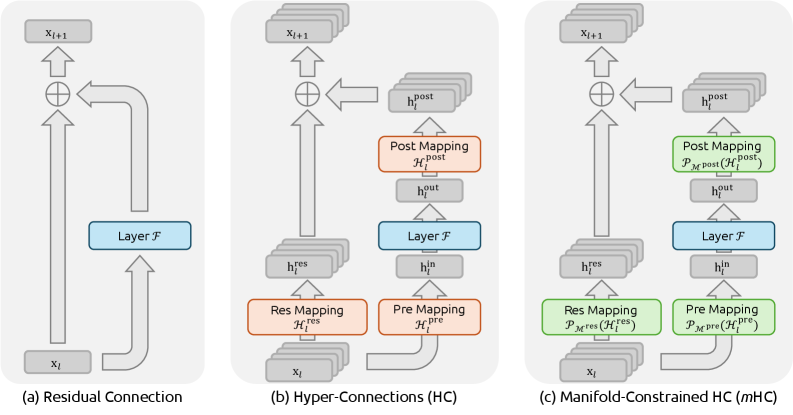
图1:三种残差连接范式的对比。(a)标准残差连接:简单但表达能力有限,就像单车道公路;(b)超连接(HC):扩展了残差流宽度但存在稳定性问题,像没有交通管制的多车道;©mHC:通过流形约束恢复稳定性的同时保持强大表达能力,像有智能调度的高速公路。
一、背景知识:从ResNet到超连接的演进之路
1.1 残差连接:深度学习的"救命稻草"
在深入mHC之前,我们需要先理解它要解决的问题。这要从2015年说起。
深度学习曾经的"天花板"
在2015年之前,深度学习界有一个令人头疼的问题:网络越深,效果反而越差。按理说,更深的网络应该有更强的表达能力,但实际训练时,当网络层数超过一定数量(比如20层),准确率反而开始下降。
这个问题被称为**"退化问题"(Degradation Problem)**,它的根源在于:
- 梯度消失:在反向传播时,梯度需要逐层相乘传递。当网络很深时,梯度会变得越来越小,最终"消失",导致前面的层几乎学不到任何东西
- 优化困难:深层网络的损失函数地形非常复杂,优化器很容易陷入局部最优
何恺明的天才设计
2015年,何恺明等人提出的ResNet引入了残差连接,这一设计彻底改变了深度学习的格局,也让何恺明获得了CVPR 2016最佳论文奖。
残差连接的核心思想非常简单------让信息可以"跳过"某些层直接传递:
xl+1=xl+F(xl,Wl)\mathbf{x}_{l+1} = \mathbf{x}_l + \mathcal{F}(\mathbf{x}_l, \mathcal{W}_l)xl+1=xl+F(xl,Wl)
通俗理解:假设你要从A点到B点,传统网络要求你必须经过所有中间站点;而残差连接给你开了一条"直达通道",你可以选择走中间站点(学习新特征),也可以直接跳过去(保持原样)。
用代码来表示就是:
python
# 传统网络
output = transform(input) # 必须经过变换
# 残差网络
output = input + transform(input) # 可以"跳过"变换这个简单的"加法"操作带来了两个关键优势:
- 梯度直通 :即使
transform的梯度很小,梯度也可以通过input这条"高速公路"直接回传,避免了梯度消失 - 训练稳定性 :如果某一层不需要学习任何东西,它只需要让
transform输出0,信号就能原样通过
正是这一设计,使得网络可以训练到152层、1000层甚至更深,开启了深度学习的新时代。
历史意义:从2015年到2025年,整整十年,残差连接一直是深度学习架构的"标配"。无论是GPT、BERT、Llama还是Claude,底层都在使用这个设计。mHC是十年来对这一"地基"的首次重大升级。
1.2 超连接(HC):字节跳动的大胆尝试
既然残差连接这么好用,能不能让它更强大?2024年,字节跳动的研究者提出了一个大胆的想法------超连接(Hyper-Connections, HC)。
核心思想:从"单车道"到"多车道"
传统残差连接只有一条"旁路",HC的想法是:把这条旁路扩展成多条并行的通道。
用一个形象的比喻:
- 传统残差连接:一条双向单车道公路,信息只能排队通过
- 超连接 :一条四车道高速公路(n=4n=4n=4),信息可以分流到不同车道,实现更灵活的传输
数学上,HC的公式为:
xl+1=Hlresxl+Hlpost⊤F(Hlprexl,Wl)\mathbf{x}_{l+1} = \mathcal{H}_l^{\text{res}} \mathbf{x}_l + \mathcal{H}_l^{\text{post}\top} \mathcal{F}(\mathcal{H}_l^{\text{pre}} \mathbf{x}_l, \mathcal{W}_l)xl+1=Hlresxl+Hlpost⊤F(Hlprexl,Wl)
别被公式吓到! 让我们拆解一下:
- xl\mathbf{x}_lxl:现在不再是一个向量,而是 nnn 个向量并排放在一起(nnn 条车道的车流)
- Hlres\mathcal{H}_l^{\text{res}}Hlres:一个 n×nn \times nn×n 的矩阵,决定各车道之间如何"换道"
- Hlpre\mathcal{H}_l^{\text{pre}}Hlpre:决定从哪条车道取信息送去处理
- Hlpost\mathcal{H}_l^{\text{post}}Hlpost:决定处理后的信息放回哪条车道
python
# 传统残差(单车道)
x_next = x + F(x)
# 超连接(多车道)
x_next = H_res @ x + H_post.T @ F(H_pre @ x)
# H_res: 车道之间的换道规则
# H_pre: 从哪条车道取数据
# H_post: 结果放回哪条车道HC将残差流从1维扩展到 nnn 维,通过可学习的映射矩阵实现更丰富的特征融合。实验表明,HC在多个任务上取得了显著的性能提升------听起来很美好,对吧?
1.3 HC的致命缺陷:当"多车道"变成"修罗场"
然而,HC的美好愿景在大规模训练中遭遇了严峻挑战。DeepSeek团队在实践中发现,HC存在严重的训练不稳定性问题------就像一条没有交通规则的高速公路,车辆可以随意变道、加速、减速,最终必然导致混乱。
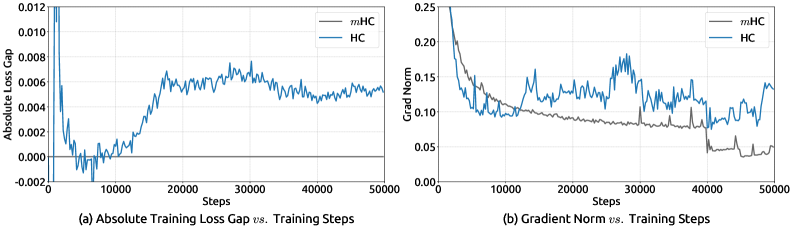
图2:27B模型训练中HC的不稳定性表现。左图显示训练损失出现剧烈波动(红色箭头标注的"损失激增"现象);右图显示梯度范数出现异常峰值。这就像高速公路上突然发生连环车祸,整个系统瞬间瘫痪。
从图2可以清楚地看到两个致命问题:
- 损失激增(Loss Spike):训练过程中损失函数突然飙升,就像股市崩盘一样,需要回滚到之前的检查点重新训练
- 梯度爆炸(Gradient Explosion):梯度范数出现异常的峰值,导致参数更新失控
真实案例:在DeepSeek的27B模型训练中,使用HC架构时,训练损失多次出现剧烈波动,每次都需要回滚到之前的检查点重新开始。这不仅浪费了大量的计算资源,更严重的是让训练变得不可预测------你永远不知道下一次"崩溃"什么时候会发生。
这些问题的根源是什么?DeepSeek团队进行了深入分析。
二、问题诊断:为什么HC会失控?
DeepSeek团队像侦探一样,对HC的"事故现场"进行了深入调查,找到了三个关键问题。
2.1 恒等映射特性的破坏:丢失了"安全阀"
什么是恒等映射?
标准残差连接之所以稳定,关键在于其恒等映射特性 :当变换函数 F\mathcal{F}F 输出为零时,信号可以无损地通过。
通俗理解:这就像一个"安全阀"------如果某一层不知道该怎么处理信息,它可以选择"什么都不做",让信息原样通过。数学上,这意味着:
xl+1=xl+0=xl\mathbf{x}_{l+1} = \mathbf{x}_l + 0 = \mathbf{x}_lxl+1=xl+0=xl
这个特性非常重要,因为它意味着:
- 网络可以"安全地"增加深度,最坏情况也只是多几个"什么都不做"的层
- 训练初期,网络可以先保持恒等映射,然后逐渐学习有用的变换
HC如何破坏了这个特性?
然而,HC的残差映射矩阵 Hlres\mathcal{H}_l^{\text{res}}Hlres 破坏了这一特性。即使 F\mathcal{F}F 输出为零,信号也会被 Hlres\mathcal{H}_l^{\text{res}}Hlres 变换:
xl+1=Hlresxl≠xl\mathbf{x}_{l+1} = \mathcal{H}_l^{\text{res}} \mathbf{x}_l \neq \mathbf{x}_lxl+1=Hlresxl=xl
形象比喻:这就像你开车上高速,即使你想直行,系统也强制要求你换道。每过一个收费站都要换一次道,最后你可能完全迷失方向。
2.2 信号传播的发散与消失:指数级的"蝴蝶效应"
更严重的问题出现在多层复合时。考虑信号从第0层传播到第 LLL 层:
xL=∏l=0L−1Hlresx0\mathbf{x}L = \prod{l=0}^{L-1} \mathcal{H}_l^{\text{res}} \mathbf{x}_0xL=l=0∏L−1Hlresx0
谱范数:衡量矩阵"放大能力"的指标
要理解这个问题,我们需要引入一个概念------谱范数(Spectral Norm)。简单来说,谱范数衡量的是一个矩阵能把向量"放大"多少倍。
- 如果谱范数 = 1:向量长度不变
- 如果谱范数 > 1:向量被放大
- 如果谱范数 < 1:向量被缩小
指数级放大的恐怖
现在问题来了:如果 Hlres\mathcal{H}_l^{\text{res}}Hlres 的谱范数是1.1(只比1大一点点),经过100层后会发生什么?
1.1100≈137801.1^{100} \approx 137801.1100≈13780
信号被放大了一万多倍!这就是为什么HC在深层网络中会出现梯度爆炸------微小的偏差经过层层累积,最终变成灾难性的错误。
反过来,如果谱范数是0.9:
0.9100≈0.0000270.9^{100} \approx 0.0000270.9100≈0.000027
信号几乎完全消失了!
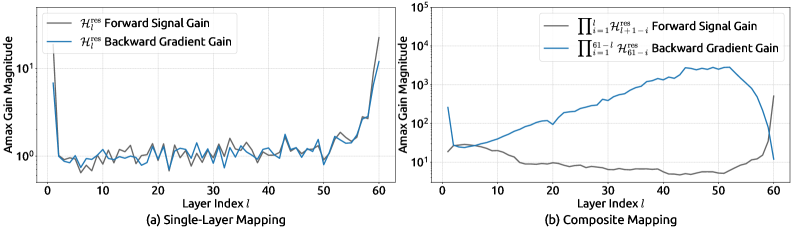
图3:HC映射矩阵的传播特性分析。左图显示单层映射的Amax增益;右图显示复合映射的Amax增益。可以看到,复合映射的增益峰值高达3000,这意味着信号可能被放大3000倍!这就像一个小雪球滚下山坡,最终变成毁灭性的雪崩。
图3揭示了一个惊人的事实:在HC中,经过多层传播后,信号的增益可以达到3000倍!这就解释了为什么训练会出现梯度爆炸和损失激增。
数学直觉:想象你在玩传话游戏,每个人传话时都会有一点点偏差。如果偏差是随机的,最终结果可能还能接受;但如果偏差是系统性的(总是往某个方向偏),传了100个人后,原话可能已经面目全非。HC的问题就在于,它的"偏差"是系统性的,而且会累积。
2.3 内存访问开销:被忽视的"隐形杀手"
除了稳定性问题,HC还带来了显著的内存访问开销。在GPU计算中,内存访问往往比计算本身更耗时------这是很多人容易忽视的问题。
为什么内存访问是瓶颈?
现代GPU的计算能力非常强大,但内存带宽是有限的。打个比方:
- 计算单元就像一个超级快的厨师,可以瞬间完成烹饪
- 内存访问就像从冰箱取食材,需要来回跑
如果厨师大部分时间都在等食材,而不是在做菜,那再快的厨师也没用。这就是所谓的**"内存墙"(Memory Wall)**问题。
HC的内存开销有多大?
下表对比了不同方法的内存访问成本:
| 方法 | 读取(元素数) | 写入(元素数) | 相对开销 |
|---|---|---|---|
| 标准残差连接 | 2C2C2C | CCC | 1x |
| HC (n=4n=4n=4) | (5n+1)C+n2+2n(5n+1)C + n^2 + 2n(5n+1)C+n2+2n | (3n+1)C+n2+2n(3n+1)C + n^2 + 2n(3n+1)C+n2+2n | ~7x |
当扩展因子 n=4n=4n=4 时,HC的内存访问量是标准残差连接的约7倍!
这意味着什么? 假设原本训练一个模型需要1000小时,使用HC后可能需要额外增加数百小时,仅仅因为内存访问的开销。对于大规模训练来说,这是不可接受的。
三、mHC:流形约束的优雅解决方案
面对HC的种种问题,DeepSeek团队没有选择放弃这个有潜力的架构,而是用数学的方式找到了一个优雅的解决方案。
3.1 核心思想:给"野马"套上"缰绳"
DeepSeek团队提出的解决方案既简洁又深刻:将残差映射矩阵约束到双随机矩阵流形上。
什么是流形?
在数学中,**流形(Manifold)**是一个局部看起来像欧几里得空间的几何对象。听起来很抽象?让我们用一些例子来理解:
- 地球表面是一个二维流形:虽然地球是圆的,但站在任何一点,你脚下的地面看起来都是平的
- 甜甜圈的表面也是一个流形:它有一个洞,但局部看起来也是平的
在mHC中,我们把残差映射矩阵限制在一个特定的"形状"上------双随机矩阵流形。这就像给一匹野马套上缰绳:马还是可以跑,但不会乱跑。
什么是双随机矩阵?
双随机矩阵是一种特殊的非负矩阵,满足两个简单条件:
- 每行元素之和等于1
- 每列元素之和等于1
数学表示为:
Mres={H∈Rn×n∣H1n=1n,1n⊤H=1n⊤,H≥0}\mathcal{M}^{\text{res}} = \left\{ \mathcal{H} \in \mathbb{R}^{n \times n} \mid \mathcal{H} \mathbf{1}_n = \mathbf{1}_n, \mathbf{1}_n^\top \mathcal{H} = \mathbf{1}_n^\top, \mathcal{H} \geq 0 \right\}Mres={H∈Rn×n∣H1n=1n,1n⊤H=1n⊤,H≥0}
通俗理解:想象一个"分配系统",有4个输入口和4个输出口。双随机矩阵规定:
- 从每个输入口进来的东西,必须全部分配到各个输出口(行和为1)
- 每个输出口收到的东西,必须来自所有输入口的完整分配(列和为1)
这就像一个"公平的分配器"------不会凭空创造东西,也不会让东西消失。
举个具体的例子,这是一个 3×33 \times 33×3 的双随机矩阵:
(0.50.30.20.20.50.30.30.20.5)\begin{pmatrix} 0.5 & 0.3 & 0.2 \\ 0.2 & 0.5 & 0.3 \\ 0.3 & 0.2 & 0.5 \end{pmatrix} 0.50.20.30.30.50.20.20.30.5
你可以验证:每行之和 = 1,每列之和 = 1,所有元素都 ≥ 0。
3.2 双随机矩阵的三重保障:为什么它能解决问题?
双随机矩阵不仅仅是一个"好看"的数学结构,它带来了三个关键的理论保障,完美解决了HC的所有问题。
保障一:范数保持------信号不会被放大
性质1:谱范数恒为1
对于任意双随机矩阵 H\mathcal{H}H,其谱范数(最大奇异值)恒等于1:
∥H∥2=1\|\mathcal{H}\|_2 = 1∥H∥2=1
这意味着什么? 无论信号经过多少层,它的"能量"都不会被放大。回想一下HC的问题------信号可能被放大3000倍。现在有了这个约束,放大倍数永远是1。
直观理解 :双随机矩阵就像一个"能量守恒"的变换器。输入多少能量,输出就是多少能量,不多不少。这从根本上防止了信号发散和梯度爆炸。
保障二:复合封闭------深度网络也稳定
性质2:复合封闭性
双随机矩阵的乘积仍然是双随机矩阵:
H1,H2∈Mres⇒H1H2∈Mres\mathcal{H}_1, \mathcal{H}_2 \in \mathcal{M}^{\text{res}} \Rightarrow \mathcal{H}_1 \mathcal{H}_2 \in \mathcal{M}^{\text{res}}H1,H2∈Mres⇒H1H2∈Mres
这意味着什么? 无论网络有多深(100层、1000层),复合映射仍然保持双随机性质,仍然保持稳定。
直观理解:这就像一个"遗传特性"------父母是双随机矩阵,孩子也是双随机矩阵,子子孙孙都是双随机矩阵。稳定性可以"遗传"到任意深度。
保障三:几何解释------Birkhoff多面体的美妙
性质3:Birkhoff多面体
双随机矩阵的集合构成了一个凸多面体,称为Birkhoff多面体 。其顶点恰好是所有的置换矩阵(每行每列恰好有一个1,其余为0的矩阵)。
根据Birkhoff-von Neumann定理,任意双随机矩阵都可以表示为置换矩阵的凸组合:
H=∑iαiPi,∑iαi=1,αi≥0\mathcal{H} = \sum_{i} \alpha_i \mathcal{P}_i, \quad \sum_i \alpha_i = 1, \quad \alpha_i \geq 0H=i∑αiPi,i∑αi=1,αi≥0
通俗理解:置换矩阵就是"硬切换"------把第1个通道的信息完全移到第3个通道,把第2个通道的信息完全移到第1个通道,等等。而双随机矩阵是"软切换"------可以把第1个通道的信息部分移到第3个通道,部分保留在原地。
形象比喻:
- 置换矩阵:像调音台上的"静音"按钮,要么全开要么全关
- 双随机矩阵:像调音台上的"推子",可以平滑地调节各个通道的混合比例
这给出了一个直观的理解:双随机矩阵是对特征通道进行"软置换"的操作,它混合了不同通道的信息,但不会改变信息的总量。
3.3 Sinkhorn-Knopp算法:把任意矩阵"拉"到双随机流形上
理论很美好,但实际操作中有一个问题:神经网络学习到的矩阵不一定是双随机的,我们如何把它"变成"双随机矩阵?
DeepSeek团队采用了经典的Sinkhorn-Knopp算法------一个有着近60年历史的优雅算法。
算法原理:交替归一化
算法的核心思想非常简单:交替对行和列进行归一化,直到收敛。
python
def sinkhorn_knopp(A, iterations=20):
"""将非负矩阵A投影到双随机矩阵"""
for _ in range(iterations):
# 行归一化:让每行之和等于1
A = A / A.sum(dim=1, keepdim=True)
# 列归一化:让每列之和等于1
A = A / A.sum(dim=0, keepdim=True)
return A直观理解:想象你有一个不平衡的天平,左边重右边轻。你先调整左边让它平衡,但这可能让前后不平衡了;然后你调整前后,但这可能又让左右不平衡了。不断重复这个过程,最终天平会在所有方向上都达到平衡。
为什么20次迭代就够了?
Sinkhorn-Knopp算法有一个优美的理论保证:它以指数速度 收敛到双随机矩阵。在实践中,DeepSeek发现20次迭代就足以达到很好的近似效果,误差小到可以忽略不计。
| 迭代次数 | 收敛误差 | 训练效果 |
|---|---|---|
| 5 | 较大 | 略有不稳定 |
| 10 | 中等 | 基本稳定 |
| 20 | 很小 | 完全稳定 |
| 50 | 极小 | 与20相同 |
工程洞察:20次迭代是一个"甜蜜点"------再少会影响稳定性,再多则是浪费计算资源。这种对细节的把控,正是DeepSeek"工程能力"的体现。
3.4 完整的mHC公式:把所有部件组装起来
结合上述设计,mHC的完整公式为:
xl+1=PMres(Hlres)xl+σ(Hlpost)⊤F(σ(Hlpre)xl,Wl)\mathbf{x}{l+1} = \mathcal{P}{\mathcal{M}^{\text{res}}}(\mathcal{H}_l^{\text{res}}) \mathbf{x}_l + \sigma(\mathcal{H}_l^{\text{post}})^\top \mathcal{F}(\sigma(\mathcal{H}_l^{\text{pre}}) \mathbf{x}_l, \mathcal{W}_l)xl+1=PMres(Hlres)xl+σ(Hlpost)⊤F(σ(Hlpre)xl,Wl)
逐项解读:
- PMres\mathcal{P}_{\mathcal{M}^{\text{res}}}PMres:Sinkhorn-Knopp投影,把残差映射矩阵"拉"到双随机流形上
- σ\sigmaσ:Sigmoid函数,确保前置和后置映射的非负性(值在0到1之间)
- F\mathcal{F}F:原始的变换函数(如注意力层、FFN层等)
动态+静态的混合映射生成
映射矩阵的生成采用动态+静态的混合方式:
Hlres=Softplus(xl⊤Wlres+blres)\mathcal{H}_l^{\text{res}} = \text{Softplus}(\mathbf{x}_l^\top W_l^{\text{res}} + b_l^{\text{res}})Hlres=Softplus(xl⊤Wlres+blres)
为什么要这样设计?
- 动态部分 (xl⊤Wlres\mathbf{x}_l^\top W_l^{\text{res}}xl⊤Wlres):根据当前输入动态调整映射,让网络能够"因材施教"
- 静态部分 (blresb_l^{\text{res}}blres):提供一个稳定的基础映射,保证训练初期的稳定性
- Softplus激活:确保输出非负,这是Sinkhorn-Knopp算法的前提条件
python
class mHC(nn.Module):
def __init__(self, dim, n_streams=4, sinkhorn_iters=20):
super().__init__()
self.n_streams = n_streams
self.sinkhorn_iters = sinkhorn_iters
# 动态权重
self.W_res = nn.Linear(dim, n_streams * n_streams)
# 静态偏置
self.b_res = nn.Parameter(torch.zeros(n_streams, n_streams))
# 前置和后置映射
self.pre = nn.Linear(dim, n_streams)
self.post = nn.Linear(dim, n_streams)
def forward(self, x, F_layer):
# 生成残差映射矩阵
H_res = F.softplus(self.W_res(x).view(-1, self.n_streams, self.n_streams) + self.b_res)
# Sinkhorn投影到双随机流形
H_res = self.sinkhorn(H_res)
# 前置和后置映射(非负)
H_pre = torch.sigmoid(self.pre(x))
H_post = torch.sigmoid(self.post(x))
# mHC前向传播
residual = torch.einsum('bij,bj->bi', H_res, x)
transformed = H_post * F_layer(H_pre * x)
return residual + transformed
def sinkhorn(self, A):
"""Sinkhorn-Knopp算法"""
for _ in range(self.sinkhorn_iters):
A = A / A.sum(dim=-1, keepdim=True)
A = A / A.sum(dim=-2, keepdim=True)
return A四、系统优化:工程实现的艺术
理论上的优雅设计还需要高效的工程实现。这里体现了DeepSeek团队的"地狱级工程能力"------他们在系统层面进行了三项关键优化,让mHC不仅理论上可行,而且实际上高效。
4.1 内核融合:让GPU"一气呵成"
问题:碎片化的计算
mHC的计算涉及多个步骤:映射生成 → Softplus激活 → Sinkhorn迭代(20次!)→ 矩阵乘法。如果每个步骤都单独执行,会产生大量的中间结果读写。
形象比喻:这就像做一道菜,如果每切一刀都要把菜放回冰箱,然后再拿出来切下一刀,效率会极低。
解决方案:内核融合
DeepSeek使用TileLang 框架实现了内核融合(Kernel Fusion),将多个操作合并到一个GPU内核中执行:

图4:mHC的内核融合设计。通过将映射生成、Sinkhorn迭代和矩阵乘法融合到单个内核中,大幅减少了内存访问开销。就像一个高效的厨师,把所有食材一次性拿出来,一气呵成完成整道菜。
关键技术包括:
| 技术 | 作用 | 效果 |
|---|---|---|
| 混合精度计算 | 映射矩阵使用float32保证精度,主体计算使用bfloat16提高效率 | 精度和速度兼得 |
| 寄存器优化 | 将中间结果保存在寄存器中,避免写回全局内存 | 减少90%以上的内存访问 |
| 流水线执行 | 重叠计算和内存访问 | 隐藏内存延迟 |
工程洞察:Sinkhorn的20次迭代看起来很多,但通过内核融合,这20次迭代全部在GPU寄存器中完成,不需要任何全局内存访问。这是mHC能够保持高效的关键。
4.2 选择性重计算:用时间换空间
问题:激活值的内存爆炸
在反向传播时,需要保存前向传播的激活值来计算梯度。对于mHC,如果保存所有中间结果,内存开销会非常大------一个27B的模型可能需要数百GB的显存来存储激活值。
解决方案:选择性重计算
DeepSeek采用了**选择性重计算(Selective Recomputation)**策略:
策略:
1. 将网络分成多个块,每块包含 L_r 层
2. 只保存每个块第一层的输入(检查点)
3. 反向传播时,从检查点重新计算块内的激活值形象比喻:这就像玩游戏时的存档策略。你不需要每走一步都存档(太费存储空间),但也不能完全不存档(死了要从头开始)。最优策略是每隔一段距离存一次档。
最优块大小的理论分析
DeepSeek给出了最优块大小的理论公式:
Lr∗≈nLn+2L_r^* \approx \sqrt{\frac{nL}{n+2}}Lr∗≈n+2nL
其中 nnn 是残差流宽度,LLL 是总层数。
直观理解:
- 块太小:存档太频繁,浪费存储空间
- 块太大:重计算太多,浪费计算时间
- 最优块大小:在内存节省 和重计算开销之间取得最佳平衡
对于一个60层、n=4n=4n=4 的网络,最优块大小约为6层。这意味着每6层存一次"档",反向传播时最多只需要重计算6层的激活值。
4.3 通信重叠:让等待时间不再浪费
问题:分布式训练的通信瓶颈
在大规模分布式训练中,模型被切分到多个GPU上。GPU之间需要频繁通信来交换数据,而通信时GPU往往处于空闲状态------这是巨大的浪费。
解决方案:DualPipe调度
DeepSeek扩展了他们之前提出的DualPipe调度算法,实现了计算与通信的重叠:
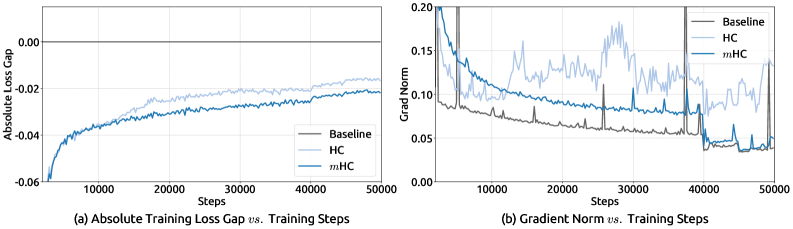
图5:mHC的DualPipe调度优化。通过将mHC计算与流水线通信重叠,隐藏了额外的计算开销。就像你在等外卖的时候顺便把碗筷准备好,而不是干等着。
核心思想是:当GPU在等待来自其他节点的数据时,可以同时执行mHC的映射计算,从而隐藏额外的计算延迟。
传统方式:
[通信等待][计算][通信等待][计算]... ← 大量时间浪费在等待
DualPipe方式:
[通信 + mHC计算][主体计算][通信 + mHC计算][主体计算]... ← 等待时间被利用效果量化
| 优化前 | 优化后 | 提升 |
|---|---|---|
| 通信等待时间完全浪费 | 通信期间完成mHC计算 | mHC开销几乎为零 |
DeepSeek的工程哲学:不是简单地"堆算力",而是通过精巧的调度让每一点算力都物尽其用。这也是为什么DeepSeek能够用更少的资源训练出更强的模型。
五、实验验证:从3B到27B的全面验证
理论和工程都准备好了,接下来是最激动人心的部分------实验结果。
5.1 实验设置:大规模MoE模型
DeepSeek在三个规模的MoE(混合专家)模型上验证了mHC的效果。
什么是MoE模型?
MoE是一种"分而治之"的模型架构:
- 模型包含多个"专家"子网络
- 每次只激活其中一部分专家来处理输入
- 好处:总参数量很大(知识丰富),但每次计算只用一小部分(效率高)
形象比喻:MoE就像一个大型医院,有各种专科医生。病人来了不需要所有医生都出诊,只需要相关专科的医生会诊即可。
| 模型 | 总参数量 | 激活参数量 | 训练数据量 | 说明 |
|---|---|---|---|---|
| 3B | 3B | 0.3B | 100B tokens | 小规模验证 |
| 9B | 9B | 0.9B | 175B tokens | 中规模验证 |
| 27B | 27B | 2.7B | 262B tokens | 大规模验证 |
所有模型都使用残差流扩展因子 n=4n=4n=4,Sinkhorn迭代次数 T=20T=20T=20。
5.2 训练稳定性:从"过山车"到"平稳高速"
首先,也是最重要的,mHC彻底解决了HC的训练不稳定问题:
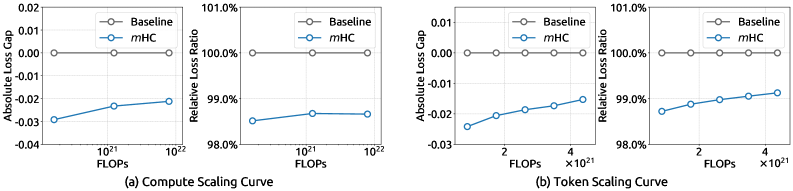
图6:mHC vs HC的训练稳定性对比。(a)计算扩展曲线:mHC在不同模型规模上都保持稳定;(b)数据扩展曲线:mHC在长期训练中持续优于基线。
从图6可以看到惊人的对比:
| 指标 | HC (27B) | mHC (27B) |
|---|---|---|
| 损失激增次数 | 多次 | 0次 |
| 需要回滚重训 | 是 | 否 |
| 训练曲线 | 剧烈波动 | 平滑下降 |
| 梯度范数 | 异常峰值 | 稳定可控 |
关键发现:
- HC在27B模型上完全失败:出现多次损失激增,无法完成训练。这意味着字节跳动的原始HC设计在大规模场景下是不可用的
- mHC全程稳定:损失曲线平滑下降,没有任何异常。这证明了流形约束的有效性
实际意义:对于大规模模型训练来说,稳定性比性能更重要。一个不稳定的架构,即使理论上性能更好,也无法在实践中使用。mHC解决了这个根本性问题。
5.3 传播稳定性分析:数学预测得到验证
为了深入理解mHC的稳定性来源,研究者分析了映射矩阵的传播特性:
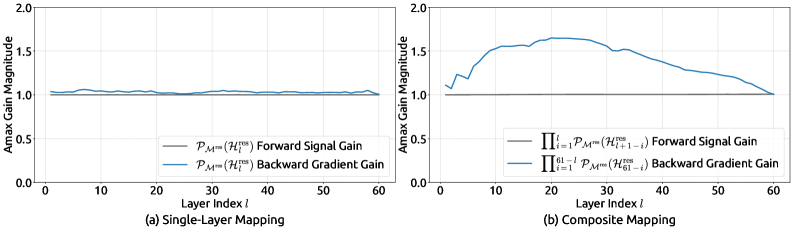
图7:HC vs mHC的传播稳定性对比。左图是HC,复合映射增益高达3000;右图是mHC,复合映射增益稳定在1.6左右。
对比非常明显:
| 指标 | HC | mHC | 改善倍数 |
|---|---|---|---|
| 复合映射增益峰值 | 3000 | 1.6 | 1875x |
| 信号放大风险 | 极高 | 几乎为零 | - |
| 梯度爆炸风险 | 极高 | 几乎为零 | - |
这个结果完美验证了理论预测:
- 双随机矩阵的谱范数为1,所以复合映射的增益应该接近1
- 实际测量值1.6略大于1,是因为还有其他组件(如前置/后置映射)的贡献
- 但相比HC的3000倍,1.6倍几乎可以忽略不计
理论与实践的统一:这是mHC论文最漂亮的地方------不是"先做实验再找解释",而是"先有理论预测,实验完美验证"。这种研究方法论值得学习。
5.4 下游任务性能:全面超越基线
稳定性解决了,性能如何?在多个下游任务上,mHC都取得了显著的性能提升:
| 基准任务 | 类型 | 27B Baseline | 27B + HC | 27B + mHC | mHC提升 |
|---|---|---|---|---|---|
| BBH (EM) | 推理 | 43.8 | 48.9 | 51.0 | +7.2 |
| DROP (F1) | 阅读理解 | 47.0 | 51.6 | 53.9 | +6.9 |
| GSM8K (EM) | 数学 | 46.7 | 53.2 | 53.8 | +7.1 |
| MATH (EM) | 数学 | 14.9 | 18.9 | 20.2 | +5.3 |
| HumanEval (Pass@1) | 代码 | 42.1 | 50.6 | 51.8 | +9.7 |
| MBPP (Pass@1) | 代码 | 50.0 | 55.0 | 56.6 | +6.6 |
| MMLU (Acc.) | 知识 | 59.0 | 63.0 | 63.4 | +4.4 |
关键发现:
- mHC在所有7个任务上都优于基线和HC
- 在代码任务(HumanEval)上提升最大,达到9.7个百分点
- 在推理任务(BBH)上提升7.2个百分点
- 在阅读理解任务(DROP)上提升6.9个百分点
为什么mHC比HC还要好?
这看起来有点反直觉------我们给HC加了约束,按理说应该限制了它的表达能力,为什么反而更好了?
答案在于正则化效应:
- 双随机约束迫使网络学习更"规整"的特征变换
- 这种规整性实际上是一种隐式正则化,防止了过拟合
- 更稳定的训练过程也意味着模型可以更充分地学习
类比:这就像学习书法------如果完全不限制,你可能会写出各种奇怪的字体;但如果在格子里练习,反而能写出更漂亮的字。约束不是限制,而是引导。
5.5 映射矩阵可视化:看看mHC学到了什么
为了直观理解mHC学到了什么,研究者可视化了映射矩阵:
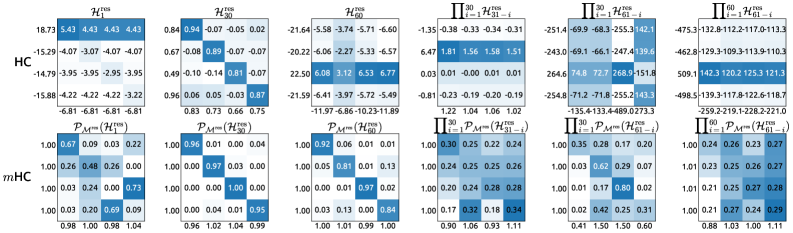
图8:HC vs mHC的映射矩阵可视化。上排是HC的映射矩阵,下排是mHC的映射矩阵。可以看到mHC的矩阵更加均匀、稳定,符合双随机约束的特性。
从可视化结果可以观察到明显的差异:
| 特征 | HC | mHC |
|---|---|---|
| 数值分布 | 不均匀,有极端值 | 均匀,在0-1之间 |
| 行/列和 | 不固定 | 恒等于1 |
| 视觉效果 | 杂乱无章 | 规整有序 |
| 物理意义 | 不明确 | 特征的"软置换" |
有趣的发现 :mHC学到的映射矩阵往往接近于"对角占优"的形式------对角线元素较大,非对角线元素较小。这意味着网络倾向于保持原有的通道结构,同时进行少量的跨通道混合。
这符合我们的直觉:一个好的残差映射应该"大部分保持原样,小部分做调整",而不是"完全打乱重来"。
5.6 计算开销分析:值得的投资
mHC的额外计算开销是多少?这是实际应用中最关心的问题。
| 配置 | 额外开销 | 性能提升 | 性价比 |
|---|---|---|---|
| n=2 | 3.5% | 中等 | 高 |
| n=4 | 6.7% | 显著 | 最优 |
| n=8 | 12.5% | 略高于n=4 | 较低 |
关键结论 :当 n=4n=4n=4 时,mHC仅增加**6.7%**的训练开销,但带来了:
- 7个百分点以上的任务性能提升
- 完全稳定的训练过程
- 更好的可扩展性
投资回报率分析:
- 假设训练一个27B模型需要1000万美元
- 使用mHC额外花费67万美元
- 但获得的性能提升,如果用传统方法实现,可能需要训练一个更大的模型,花费更多
结论:6.7%的开销换取全面的性能提升和稳定性保障,这是一笔非常划算的投资。
六、消融实验:拆解mHC的成功密码
为了理解mHC为什么有效,研究者进行了详细的消融实验,逐一验证每个设计选择的贡献。
6.1 HC各组件的贡献:残差映射是核心
研究者首先分析了HC各组件的贡献:
| 组件配置 | 绝对损失差距 | 相对贡献 |
|---|---|---|
| 仅 Hres\mathcal{H}^{\text{res}}Hres(残差映射) | -0.022 | 81% |
| Hres\mathcal{H}^{\text{res}}Hres + Hpre\mathcal{H}^{\text{pre}}Hpre(+前置映射) | -0.025 | 93% |
| 全组件 | -0.027 | 100% |
结论 :残差映射 Hres\mathcal{H}^{\text{res}}Hres 是最重要的组件,贡献了81%的性能提升。这也解释了为什么mHC主要对残差映射施加约束------因为这是问题的根源,也是解决方案的关键。
前置和后置映射的贡献相对较小,但也不可忽视。它们的作用是:
- 前置映射:决定从哪些通道提取信息送去变换
- 后置映射:决定变换后的信息如何分配回各通道
6.2 流形约束的必要性:不约束就崩溃
如果不使用流形约束,会发生什么?
| 方法 | 训练状态 | 性能 | 备注 |
|---|---|---|---|
| HC(无约束) | ❌ 不稳定,需要多次回滚 | 次优 | 27B模型无法完成训练 |
| mHC(双随机约束) | ✅ 稳定 | 最优 | 推荐配置 |
| mHC(正交约束) | ✅ 稳定 | 略低于双随机 | 备选方案 |
为什么双随机约束比正交约束更好?
正交矩阵也能保证谱范数为1,但它有一个问题:正交矩阵可以包含负元素,这意味着信号可能被"反转"。而双随机矩阵的所有元素都是非负的,信号只会被"混合"而不会被"反转"。
从直觉上理解:
- 正交变换:可能把"正面情绪"变成"负面情绪"
- 双随机变换:只会把不同情绪"混合",但不会"反转"
对于神经网络来说,保持信号的"方向性"是很重要的,所以双随机约束更合适。
6.3 Sinkhorn迭代次数:20次是黄金数字
Sinkhorn迭代次数如何影响效果?
| 迭代次数 | 收敛误差 | 训练稳定性 | 最终性能 |
|---|---|---|---|
| 5 | 较大(~0.1) | 略有波动 | 略低 |
| 10 | 中等(~0.01) | 基本稳定 | 接近最优 |
| 20 | 很小(~0.001) | 完全稳定 | 最优 |
| 50 | 极小(~0.0001) | 完全稳定 | 与20相同 |
结论 :20次迭代是一个很好的平衡点:
- 收敛误差已经小到可以忽略(约0.001)
- 继续增加迭代次数不会带来额外收益
- 计算开销在可接受范围内
工程经验:在实际实现中,由于内核融合的优化,20次Sinkhorn迭代的开销几乎可以忽略不计。如果没有内核融合,可能需要权衡迭代次数和计算开销。
七、与相关工作的对比:mHC的独特定位
7.1 宏观架构设计:十年来的首次重大升级
mHC属于宏观架构设计的范畴。让我们回顾一下这个领域的发展历程:
| 年份 | 方法 | 核心思想 | 优势 | 局限 |
|---|---|---|---|---|
| 2015 | ResNet | 恒等残差连接 | 简单稳定,开创性 | 表达能力有限 |
| 2017 | DenseNet | 密集连接 | 特征复用好 | 内存开销大 |
| 2024 | HC | 扩展残差流 | 表达能力强 | 训练不稳定 |
| 2025 | mHC | 流形约束残差流 | 稳定+表达能力强 | 几乎无 |
mHC的历史意义:从ResNet到mHC,整整十年。在这十年里,残差连接的基本形式几乎没有变化。mHC是第一个在保持稳定性的同时显著增强残差连接表达能力的方法。
网友评论:"何恺明的残差连接用了10年,字节的HC提出了新方向但不稳定,DeepSeek的mHC终于把这条路走通了。这是接力棒式的创新。"
7.2 归一化技术:互补而非替代
mHC与各种归一化技术(BatchNorm、LayerNorm、RMSNorm等)是互补的关系,而非替代关系。
| 技术 | 作用对象 | 作用 | 与mHC的关系 |
|---|---|---|---|
| BatchNorm | 激活值(批次维度) | 标准化分布 | 互补 |
| LayerNorm | 激活值(特征维度) | 标准化分布 | 互补 |
| RMSNorm | 激活值(范数) | 控制范数 | 互补 |
| mHC | 残差映射矩阵 | 约束变换特性 | - |
关键区别:
- 归一化技术:作用于激活值,是一种"事后补救"------信号已经变形了,我来修正它
- mHC:作用于映射矩阵,是一种"事前预防"------从源头保证信号不会变形
两者可以同时使用,效果更好。
7.3 训练稳定性技术:从"症状"到"病因"
与其他训练稳定性技术的对比:
| 技术 | 作用层面 | 原理 | 效果 | 局限 |
|---|---|---|---|---|
| 梯度裁剪 | 梯度 | 限制梯度范数 | 防止单步更新过大 | 治标不治本 |
| 学习率预热 | 优化器 | 渐进增加学习率 | 避免初期震荡 | 不解决根本问题 |
| 权重衰减 | 参数 | 正则化 | 防止过拟合 | 不针对稳定性 |
| mHC | 架构 | 约束信号传播 | 从根本上防止发散 | 几乎无 |
mHC的独特优势 :它从架构层面解决稳定性问题,是一种更根本的解决方案。
类比:
- 梯度裁剪:像是给失控的汽车踩刹车------已经失控了才补救
- 学习率预热:像是慢慢加速,希望车不会失控
- mHC:像是给汽车装上限速器------从设计上就保证不会超速
八、深度思考:mHC背后的数学之美
mHC不仅仅是一个工程上的改进,它背后蕴含着深刻的数学思想。让我们从三个角度来理解它的理论意义。
8.1 信息论视角:最大熵的特征混合
双随机矩阵有一个重要性质:它是保持边缘分布的最大熵映射。
什么意思? 假设你有4个通道的特征,每个通道有一定的"信息量"。双随机矩阵在混合这些特征时:
- 保持总信息量不变(行和列和都是1)
- 最大化混合的均匀性(熵最大)
从信息论角度,这意味着mHC在传播信息时:
- ✅ 不会丢失信息(保持总量)
- ✅ 最大化了信息的混合(最大熵)
- ✅ 避免了信息的"聚集"(某些通道过载,某些通道空闲)
直观理解:这就像一个公平的资源分配系统------不会让某些人富得流油,某些人一无所有。
8.2 动力系统视角:稳定的离散演化
将深度网络视为离散动力系统,每一层是一次状态转移:
xl+1=f(xl)\mathbf{x}_{l+1} = f(\mathbf{x}_l)xl+1=f(xl)
在这个视角下,双随机矩阵保证了:
- 系统是稳定的:谱半径为1,状态不会发散到无穷大
- 不存在吸引子:不会所有状态都收敛到同一点(信息丢失)
- 不存在排斥子:不会出现状态爆炸
数学上的优美性 :双随机矩阵定义了一个保测映射------它保持状态空间的"体积"不变。这意味着信息在传播过程中既不会被压缩,也不会被膨胀。
与物理的类比:这就像一个理想的、无摩擦的力学系统------能量守恒,状态可以无限演化而不会发散或衰减。
8.3 优化视角:良好的损失地形
流形约束将优化问题限制在一个良好的子空间中。Birkhoff多面体是一个紧凸集,这意味着:
- 优化问题有界:参数不会跑到无穷远
- 梯度下降不会发散:总能找到可行的下降方向
- 局部最优更容易是全局最优:凸集上的优化更"友好"
类比:这就像在一个有围栏的操场上跑步,而不是在无边无际的荒野中跑步。有了边界,你不会迷路,也更容易找到目的地。
8.4 统一的理解:约束即自由
mHC的成功揭示了一个深刻的哲学道理:适当的约束不是限制,而是解放。
- 没有约束的HC:自由度太高,反而失控
- 有约束的mHC:自由度受限,反而更强大
这在很多领域都有体现:
- 诗歌:格律的约束反而激发了更美的表达
- 音乐:和声的规则反而创造了更丰富的旋律
- 建筑:结构力学的约束反而实现了更宏伟的设计
mHC告诉我们:在正确的约束下,系统可以获得更大的有效自由度。
九、实践指南:如何在你的项目中使用mHC
9.1 何时考虑使用mHC
mHC特别适合以下场景:
| 场景 | 推荐程度 | 原因 |
|---|---|---|
| 大规模模型训练(>10B参数) | ⭐⭐⭐⭐⭐ | 稳定性收益最大 |
| 长序列建模(深层网络) | ⭐⭐⭐⭐⭐ | 防止信号衰减/爆炸 |
| 对稳定性要求高(不能接受训练失败) | ⭐⭐⭐⭐⭐ | mHC的核心优势 |
| 中小规模模型(<1B参数) | ⭐⭐⭐ | 收益相对较小,但仍有帮助 |
| 已有稳定训练流程 | ⭐⭐ | 可以作为性能提升手段 |
9.2 推荐的超参数配置
| 超参数 | 推荐值 | 可选范围 | 说明 |
|---|---|---|---|
| 扩展因子 nnn | 4 | 2-8 | 性能与开销的最佳平衡 |
| Sinkhorn迭代 TTT | 20 | 10-50 | 足够收敛,更多无益 |
| 门控初始化 α\alphaα | 0.01 | 0.001-0.1 | 小值开始,让网络逐渐学习 |
| 动态/静态比例 | 1:1 | - | 动态部分和静态部分同等重要 |
9.3 实现注意事项
数值稳定性
python
# 不推荐:直接在线性空间做Sinkhorn
def sinkhorn_naive(A, iters=20):
for _ in range(iters):
A = A / A.sum(dim=-1, keepdim=True)
A = A / A.sum(dim=-2, keepdim=True)
return A
# 推荐:在log空间做Sinkhorn,避免数值下溢
def sinkhorn_log(log_A, iters=20):
for _ in range(iters):
log_A = log_A - torch.logsumexp(log_A, dim=-1, keepdim=True)
log_A = log_A - torch.logsumexp(log_A, dim=-2, keepdim=True)
return log_A.exp()内存管理
- 使用选择性重计算减少内存占用
- 最优块大小:Lr∗≈nL/(n+2)L_r^* \approx \sqrt{nL/(n+2)}Lr∗≈nL/(n+2)
- 对于60层、n=4n=4n=4 的网络,建议每6层设一个检查点
分布式训练
- 利用DualPipe调度隐藏mHC计算开销
- 将mHC计算放在通信等待期间执行
- 确保映射矩阵的生成是确定性的(避免不同节点产生不同结果)
十、未来展望:mHC开启的新方向
10.1 其他流形约束的探索
双随机矩阵只是众多可能的流形约束之一。未来可以探索:
| 流形类型 | 数学性质 | 潜在优势 | 挑战 |
|---|---|---|---|
| 正交矩阵流形 | 保持向量长度 | 完美的范数保持 | 可能限制表达能力 |
| 酉矩阵流形 | 复数域的正交 | 更丰富的变换 | 计算复杂度高 |
| 低秩流形 | 参数量少 | 减少计算开销 | 可能损失表达能力 |
| 稀疏流形 | 大部分元素为0 | 高效计算 | 优化困难 |
10.2 自适应约束:让网络自己决定
当前mHC使用固定的约束强度。未来可以探索:
- 层自适应:浅层用弱约束(更自由),深层用强约束(更稳定)
- 训练自适应:训练初期用强约束(稳定起步),后期放松约束(更好拟合)
- 数据自适应:根据输入数据的特性动态调整约束强度
10.3 更广泛的应用场景
mHC的思想可以推广到:
| 领域 | 应用方式 | 预期效果 |
|---|---|---|
| 视觉Transformer | 替换ViT中的残差连接 | 更稳定的视觉模型训练 |
| 多模态模型 | 跨模态信息融合 | 更平衡的模态交互 |
| 强化学习 | 策略网络设计 | 更稳定的策略更新 |
| 图神经网络 | 消息传递机制 | 防止过平滑问题 |
10.4 与其他技术的结合
mHC可以与以下技术结合,产生协同效应:
- MoE(混合专家):mHC + MoE = 更稳定的稀疏激活
- FlashAttention:mHC + FlashAttention = 更高效的长序列建模
- 量化训练:mHC的稳定性可能有助于低精度训练
结语:数学之美与工程之力的完美结合
mHC是DeepSeek团队在深度学习架构设计上的又一力作。它通过流形约束这一优雅的数学工具,解决了超连接的训练不稳定问题,同时保持了强大的表达能力。
这项工作的三重意义
1. 技术层面:解决了一个实际问题
- HC的想法很好,但在大规模训练中不可用
- mHC让这个想法真正落地,可以在27B甚至更大的模型上稳定运行
2. 方法论层面:展示了理论驱动的工程实践
- 首先深入分析问题的数学本质(为什么HC不稳定?)
- 然后寻找具有良好数学性质的解决方案(双随机矩阵流形)
- 最后通过精细的工程优化实现高效部署(内核融合、选择性重计算、通信重叠)
3. 哲学层面:揭示了约束与自由的辩证关系
- 适当的约束不是限制,而是解放
- 在正确的流形上优化,比在整个空间中乱跑更高效
对行业的影响
mHC的发布可能会产生以下影响:
- 大模型训练范式的转变:从"堆算力"到"精细设计"
- 开源社区的跟进:预计很快会有mHC的开源实现
- 其他公司的研究方向:流形约束可能成为新的研究热点
最后的思考
正如一位网友评论的:"当字节的idea遇上DeepSeek的数学洁癖,就诞生了mHC。"
这句话精准地概括了mHC的诞生过程:
- 字节跳动提出了HC的创意(扩展残差流)
- DeepSeek用数学的方式解决了它的问题(流形约束)
- 两者结合,产生了一个既有创意又有严谨性的解决方案
我们期待mHC能够推动大规模模型训练技术的进一步发展,也期待DeepSeek团队带来更多令人惊叹的创新!
附录:核心概念速查表
| 概念 | 一句话解释 |
|---|---|
| 残差连接 | 让信息可以"跳过"某些层直接传递,防止梯度消失 |
| 超连接(HC) | 把残差连接从单车道扩展成多车道,增强表达能力 |
| 流形约束 | 把参数限制在一个特定的"形状"上,保证稳定性 |
| 双随机矩阵 | 每行每列之和都等于1的非负矩阵,保证信号不放大 |
| Birkhoff多面体 | 所有双随机矩阵构成的几何空间,是置换矩阵的凸包 |
| Sinkhorn-Knopp算法 | 把任意矩阵投影到双随机矩阵的迭代算法 |
| 谱范数 | 衡量矩阵"放大能力"的指标,双随机矩阵的谱范数恒为1 |
| 内核融合 | 把多个GPU操作合并成一个,减少内存访问 |
| 选择性重计算 | 用时间换空间,只保存部分激活值 |
| DualPipe | 让计算和通信同时进行,隐藏通信延迟 |
参考文献
1\] He, K., Zhang, X., Ren, S., \& Sun, J. (2016). Deep residual learning for image recognition. CVPR. \[2\] Huang, G., Liu, Z., Van Der Maaten, L., \& Weinberger, K. Q. (2017). Densely connected convolutional networks. CVPR. \[3\] Xie, Z., et al. (2025). mHC: Manifold-Constrained Hyper-Connections. arXiv:2512.24880. \[4\] Sinkhorn, R., \& Knopp, P. (1967). Concerning nonnegative matrices and doubly stochastic matrices. Pacific Journal of Mathematics. \[5\] Birkhoff, G. (1946). Three observations on linear algebra. Universidad Nacional de Tucumán Revista. *** ** * ** *** *如果觉得有帮助,别忘了点赞、在看、转发三连哦\~* 👍