INT305 Machine Learning 机器学习 Pt.11 循环神经网络（RNN，Recurrent Neural Network）

文章目录

• [1. 神经网络](#1. 神经网络)
• • [1.1 AlexNet网络](#1.1 AlexNet网络)
  • [1.2 VGGNet](#1.2 VGGNet)
  • [1.3 GoogleNet](#1.3 GoogleNet)
  • [1.4 ResNet](#1.4 ResNet)
• [2. 循环神经网络（RNN，Recurrent Neural Network）](#2. 循环神经网络（RNN，Recurrent Neural Network）)
• • [2.1 结构](#2.1 结构)
  • [2.2 现有CNN的局限性](#2.2 现有CNN的局限性)
  • [2.3 RNN的结构](#2.3 RNN的结构)
  • [2.4 RNN 隐藏状态的更新](#2.4 RNN 隐藏状态的更新)
  • [2.5 RNN 的输出](#2.5 RNN 的输出)
  • [2.6 最基础的 RNN（vanilla RNN / Elman RNN）](#2.6 最基础的 RNN（vanilla RNN / Elman RNN）)
  • [2.7 结构拓展](#2.7 结构拓展)
  • • [2.7.1 Sequence-to-Sequence（Seq2Seq）模型](#2.7.1 Sequence-to-Sequence（Seq2Seq）模型)
  • [2.8 RNN应用](#2.8 RNN应用)
  • [2.9 RNN的训练方式](#2.9 RNN的训练方式)
  • • [2.9.1 截断时间反向传播（Truncated Backpropagation Through Time，TBPTT）](#2.9.1 截断时间反向传播（Truncated Backpropagation Through Time，TBPTT）)
  • [2.10 RNN 总结](#2.10 RNN 总结)
  • [2.11 更多应用](#2.11 更多应用)
  • • [2.11.1 图像字幕生成（Image Captioning）模型](#2.11.1 图像字幕生成（Image Captioning）模型)
    • [2.11.2 带注意力机制的图像描述（Image Captioning with Attention）](#2.11.2 带注意力机制的图像描述（Image Captioning with Attention）)
• [3. LSTM（Long Short-Term Memory，长短期记忆网络）](#3. LSTM（Long Short-Term Memory，长短期记忆网络）)
• • [3.1 梯度消失](#3.1 梯度消失)
  • [3.2 LSTM 的结构](#3.2 LSTM 的结构)
• [4. MLLMs（Multimodal Large Language Models，多模态大语言模型）](#4. MLLMs（Multimodal Large Language Models，多模态大语言模型）)

1. 神经网络

我们之前提到过神经网络，而且别的课程中也对神经网络进行了系统的学习。

我们再回顾一下一些著名的神经网络模型。

1.1 AlexNet网络

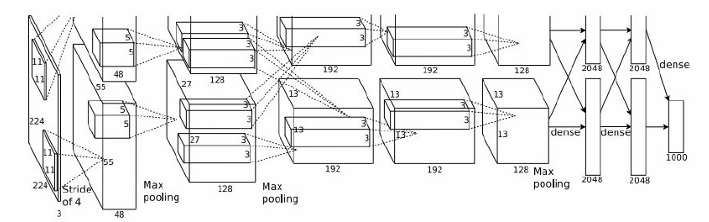
卷积层（CONV1-CONV5）：

CONV1：使用96个11x11的卷积核，步长为4，没有填充（pad 0），输出特征图尺寸为55x55x96。

POOL1：使用3x3的最大池化（Max pooling），步长为2，输出特征图尺寸为27x27x96。

NORM1：归一化层，用于标准化特征图。

CONV2：使用256个5x5的卷积核，步长为1，填充为2（pad 2），输出特征图尺寸为27x27x256。

POOL2：使用3x3的最大池化，步长为2，输出特征图尺寸为13x13x256。

NORM2：归一化层。

CONV3：使用384个3x3的卷积核，步长为1，填充为1（pad 1），输出特征图尺寸为13x13x384。

CONV4：使用384个3x3的卷积核，步长为1，填充为1（pad 1），输出特征图尺寸为13x13x384。

CONV5：使用256个3x3的卷积核，步长为1，填充为1（pad 1），输出特征图尺寸为13x13x256。

POOL3：使用3x3的最大池化，步长为2，输出特征图尺寸为6x6x256。

全连接层（FC6-FC8）：

FC6：4096个神经元的全连接层。

FC7：4096个神经元的全连接层。

FC8：1000个神经元的全连接层，用于输出类别分数。

细节：

AlexNet是第一个使用ReLU激活函数的网络。

使用了归一化层（Norm layers），这在当时并不常见。

进行了大量数据增强（Heavy data augmentation）。

使用了Dropout 0.5来防止过拟合。

批量大小（Batch size）为128。

使用了SGD动量（SGD Momentum）0.9。

学习率（Learning rate）初始为1e-2，每10个epoch减少10倍。

当验证准确率（val accuracy）稳定时手动调整学习率。

L2权重衰减（L2 weight decay）5e-4。

使用了7个CNN集成（ensemble）来提高性能，前5错误率从18.2%降低到15.4%。

1.2 VGGNet

VGGNet是由Simonyan和Zisserman在2014年提出的一种深度卷积神经网络（CNN）架构。

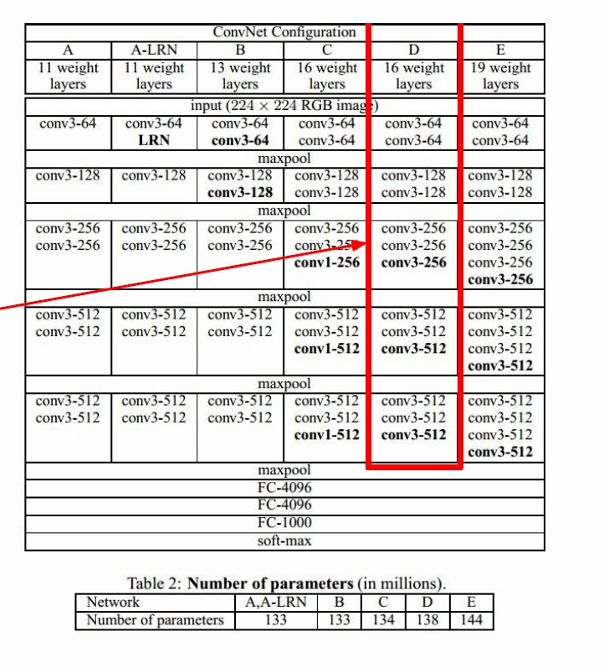
VGGNet只使用3x3的卷积核，步长为1，填充为1（pad 1）。

使用2x2的最大池化（Max Pooling），步长为2。

图中用红色框标出了VGGNet的"最佳模型"配置，即配置E。

配置E包含19个权重层，是所有配置中层数最多的。

在ILSVRC 2013（ImageNet Large Scale Visual Recognition Challenge 2013）数据集上，最佳模型的前5错误率为11.2%。

进一步优化后，错误率可以降低到7.3%。

1.3 GoogleNet

这是由Szegedy等人在2014年提出的一种深度卷积神经网络（CNN）架构。GoogLeNet在ILSVRC 2014（ImageNet Large Scale Visual Recognition Challenge）比赛中取得了优异的成绩，其top-5错误率为6.7%。

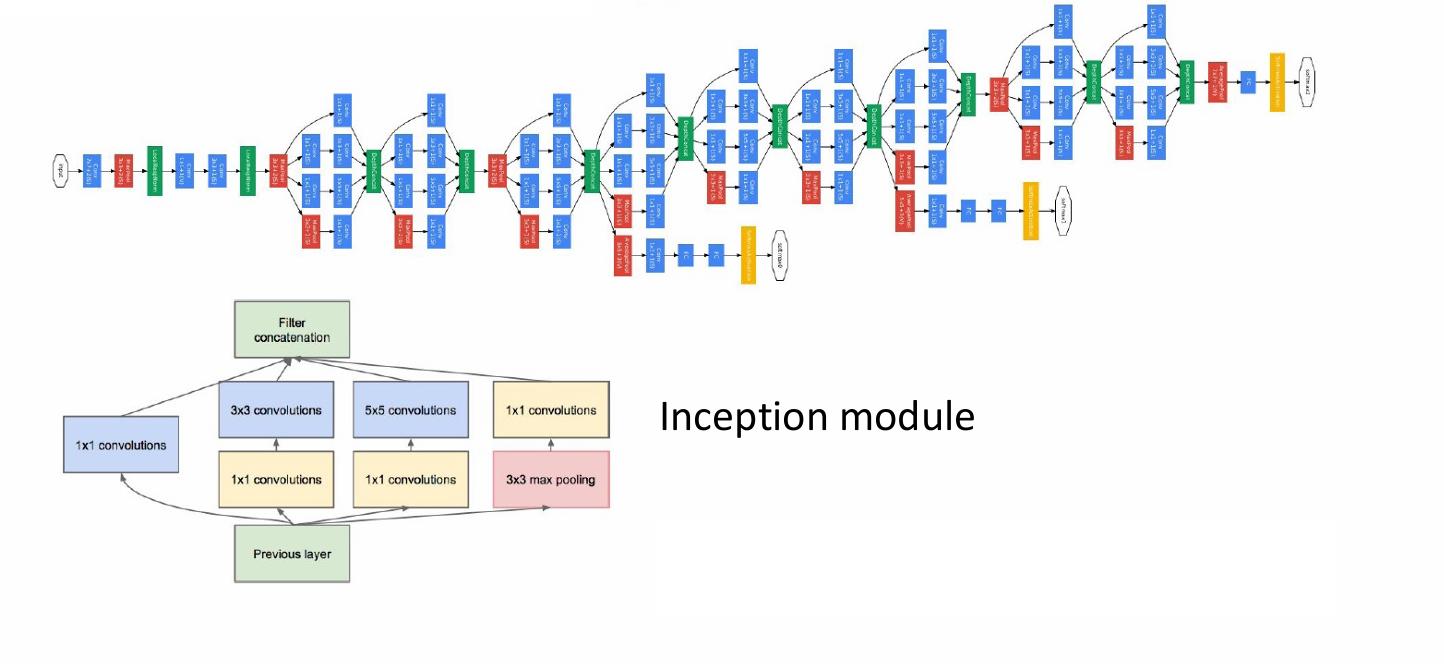
GoogLeNet由多个Inception模块堆叠而成，每个模块后通常跟随一个池化层。

Inception模块通过并行执行不同大小的卷积操作来捕获图像中的多尺度特征。

模块包括1x1、3x3和5x5的卷积操作，以及一个3x3的最大池化操作。这些操作的输出被连接（concatenated）在一起，形成模块的输出。

GoogLeNet的一个重要特性是它只有500万个参数，这比当时的其他网络少得多。

它完全去除了全连接层（FC layers），通过使用Inception模块来减少参数数量。

与AlexNet的比较：

GoogLeNet的参数数量比AlexNet少12倍。

计算量是AlexNet的两倍。

在ImageNet数据集上的top-5错误率比AlexNet低（6.67% vs. 15.4%）。

1.4 ResNet

由He等人在2015年提出。ResNet在ILSVRC 2015（ImageNet Large Scale Visual Recognition Challenge）比赛中取得了冠军，其top-5错误率为3.6%。

ResNet通过引入残差学习（residual learning）的概念，解决了深度网络训练中的退化问题，使得构建更深的网络成为可能，从而在多个视觉任务中取得了显著的性能提升。

下图中列出了从2010年到2015年的几个主要CNN架构及其在top-5错误率（即前5个预测中正确分类的比例）上的表现。

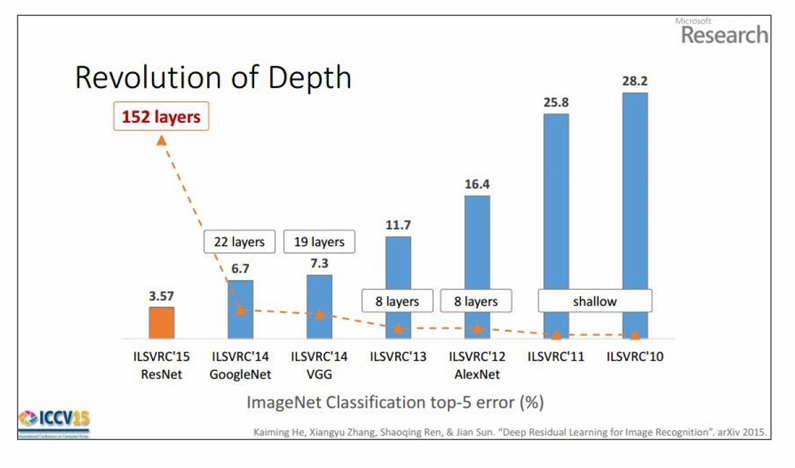
每种架构旁边标注了其层数，例如AlexNet有8层，VGG有19层，GoogLeNet有22层，而ResNet有152层。

随着CNN架构的层数增加，模型在ImageNet分类任务上的性能显著提高，特别是ResNet通过引入残差学习解决了深度网络训练的难题，实现了更低的错误率。

下图显示了不同层数（20层、32层、44层、56层、110层）的ResNet在训练和测试过程中的错误率变化。

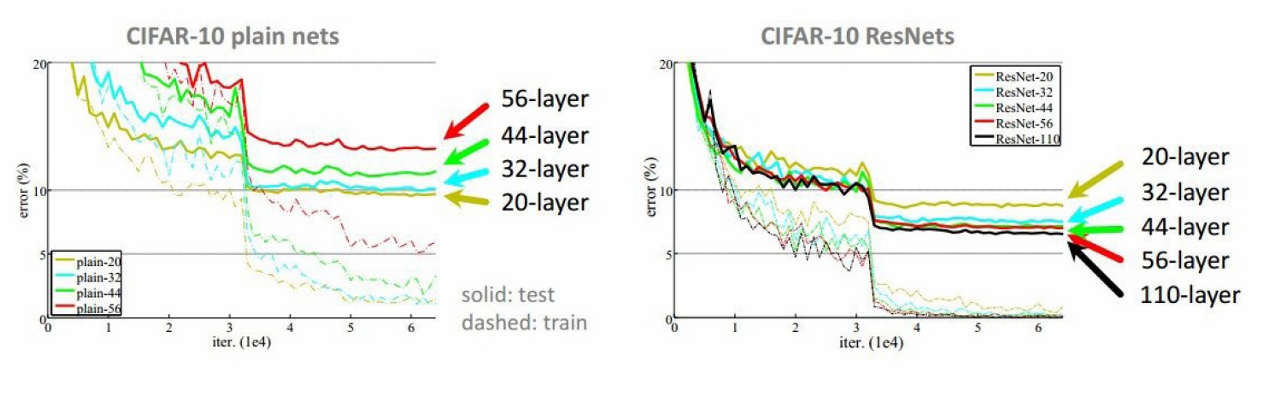
ResNet的错误率明显低于普通网络，特别是在网络层数较多时（例如56层和110层）。

随着层数的增加，ResNet的错误率持续下降，显示出更好的泛化能力和学习能力。

残差网络（ResNet）通过引入残差连接有效地解决了深度网络训练中的退化问题，使得可以构建更深的网络而不会遇到性能瓶颈。

此外esNet可以在2-3周内使用8个GPU机器完成训练。尽管ResNet的层数远多于AlexNet和VGG，但其训练效率仍然很高。这也是因为ResNet的残差连接设计使得网络更容易训练，从而在推理时也更高效。

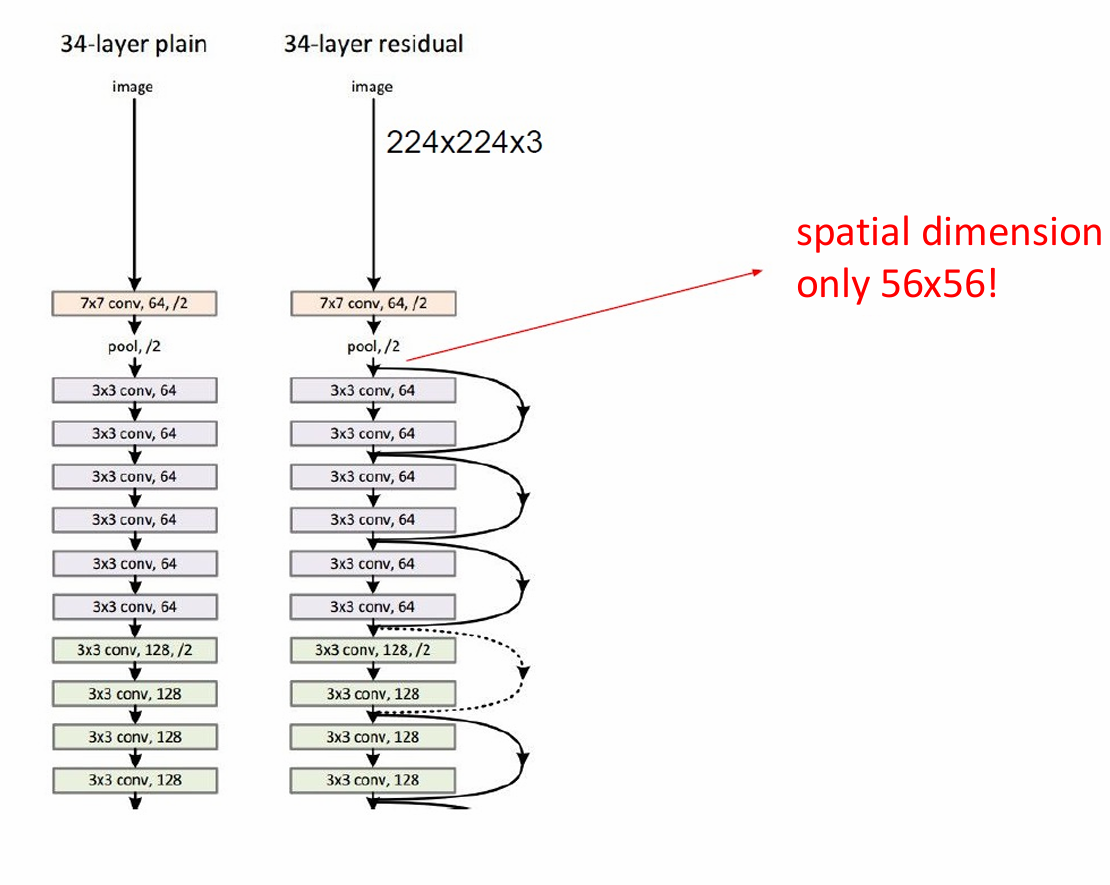
左侧展示了一个34层的普通卷积网络架构。

每一层都包含卷积层（conv）和池化层（pool）。

随着网络深度的增加，特征图的空间维度逐渐减小。

右侧展示了一个34层的残差网络架构。

残差网络通过引入残差连接来解决深度网络中的退化问题，使得网络可以更深。

图中用箭头和虚线表示残差连接，这些连接跳过了一些层，直接将输入传递到后面的层。

尽管网络更深，但空间维度（宽度和高度）仅减小到56x56，而不是像普通网络那样减小到更小的尺寸。

这种设计有助于保留更多的空间信息，从而提高网络的性能。

2. 循环神经网络（RNN，Recurrent Neural Network）

现在进入我们这次的正题------循环神经网络（RNN，Recurrent Neural Network）。

RNN的核心在于其循环结构，它将网络的输出再次输入到网络中，形成一个循环。这种结构使得网络能够利用之前时刻的信息来影响当前时刻的输出，从而捕捉序列中的时间依赖关系。

2.1 结构

RNN有多种架构类型：

一对一（One to One）：

这种架构处理固定大小的输入并产生固定大小的输出。例如，图像分类任务，其中输入是一个图像，输出是一个类别标签。

一对多（One to Many）：

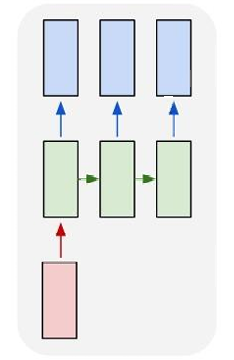
在这种架构中，单个输入对应一个序列输出。例如，图像字幕生成任务，其中输入是一个图像，输出是一系列单词（即字幕）。

多对一（Many to One）：

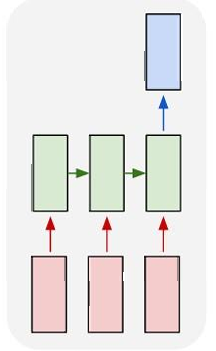
这种架构处理序列输入并产生单个输出。例如，情感分析任务，其中输入是一个句子，输出是该句子表达的是正面还是负面情感。

动作预测（Action Prediction），其中输入是一系列视频帧，输出是一个动作类别。

多对多（Many to Many）：

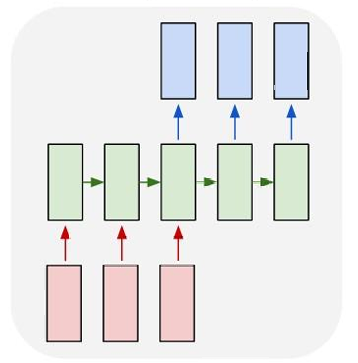
这种架构处理序列输入并产生序列输出。例如，机器翻译任务，其中输入是一个语言的句子，输出是另一种语言的句子。

视频字幕生成（Video Captioning），其中输入是一系列视频帧，输出是描述视频内容的一系列文字（字幕）。

多对多（Many to Many）同步序列输入和输出：

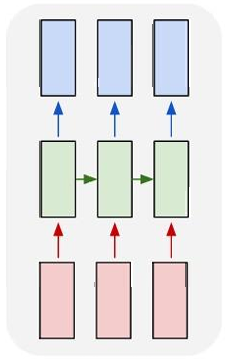
在这种架构中，输入和输出都是序列，并且它们是同步的。例如，视频分类任务，其中输入是视频的帧序列，输出是每个帧的标签。

2.2 现有CNN的局限性

现有的卷积神经网络（CNN）在处理某些任务时可能不够有效，特别是当涉及到处理具有可变序列长度的输入和输出时。

以视频字幕生成（video captioning）为例，不同的视频可能有不同的长度，即帧数（T Frames）可以变化。因此对于不同的视频，生成的字幕（Output Captions）长度也可能不同，因为每个视频的内容和复杂性不同，需要不同数量的描述来准确传达视频内容。

传统的CNN通常设计为处理固定大小的输入（例如，固定尺寸的图像）。虽然CNN可以通过滑动窗口等技术处理不同大小的图像，但它们在处理序列数据时，尤其是当序列长度变化时，可能会遇到困难。

CNN不自然地处理序列数据，因为它们缺乏内在的机制来处理时间或序列上的依赖关系，这是RNN和LSTM等循环网络所擅长的。

所以我们现在开始讲解RNN的详细结构

2.3 RNN的结构

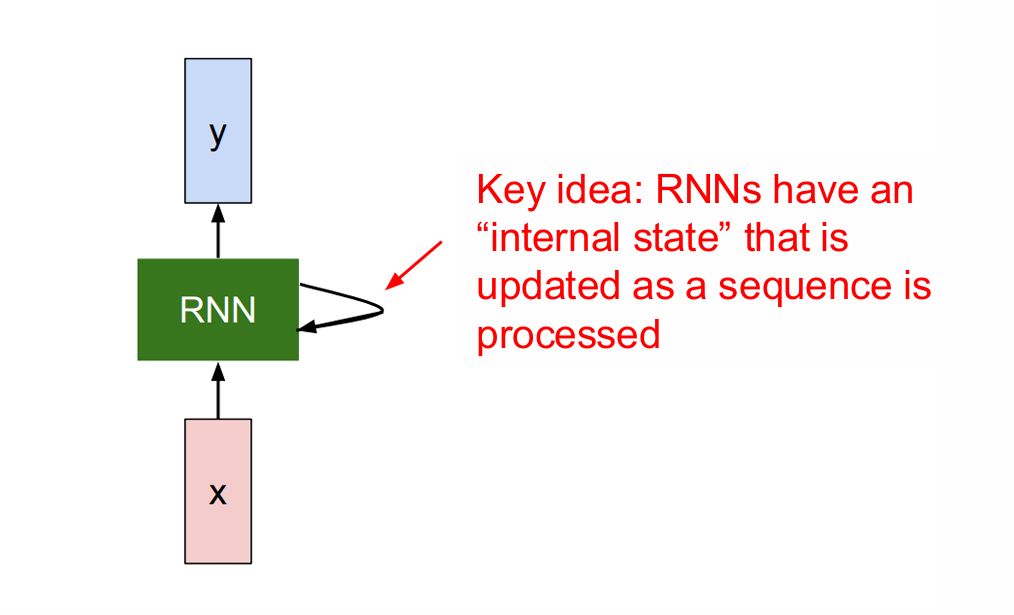
RNN 有一个名为 RNN单元 的核心模块，这个模块在序列中会被反复使用。这里 x 代表某一时刻的输入，y 代表某一时刻的输出。

RNN单元 会把"上一时刻的信息"传给下一时刻自己。这就是所谓的internal state / hidden state。

也就是说 RNN 在处理序列时，会不断更新一个内部状态。

而且它不是每一步一个新网络，而是参数完全共享。

因此 RNN 的本质是：通过隐藏状态在时间维度上传递信息，使模型在当前时刻的输出依赖于过去的输入。

所以 RNN单元 标准图如下。

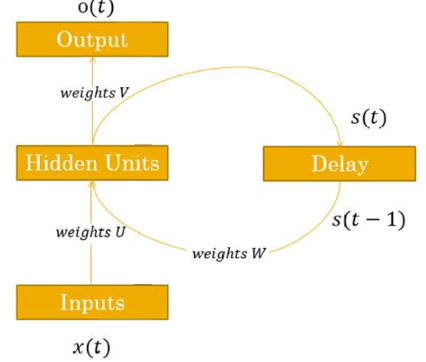
同一个 RNN单元 在不同时间步被重复使用，用来处理序列中的每一个输入。

在抽象图里，RNN 是一个带回环的方块，看不清时间关系，因此我们现在展开展示一遍。

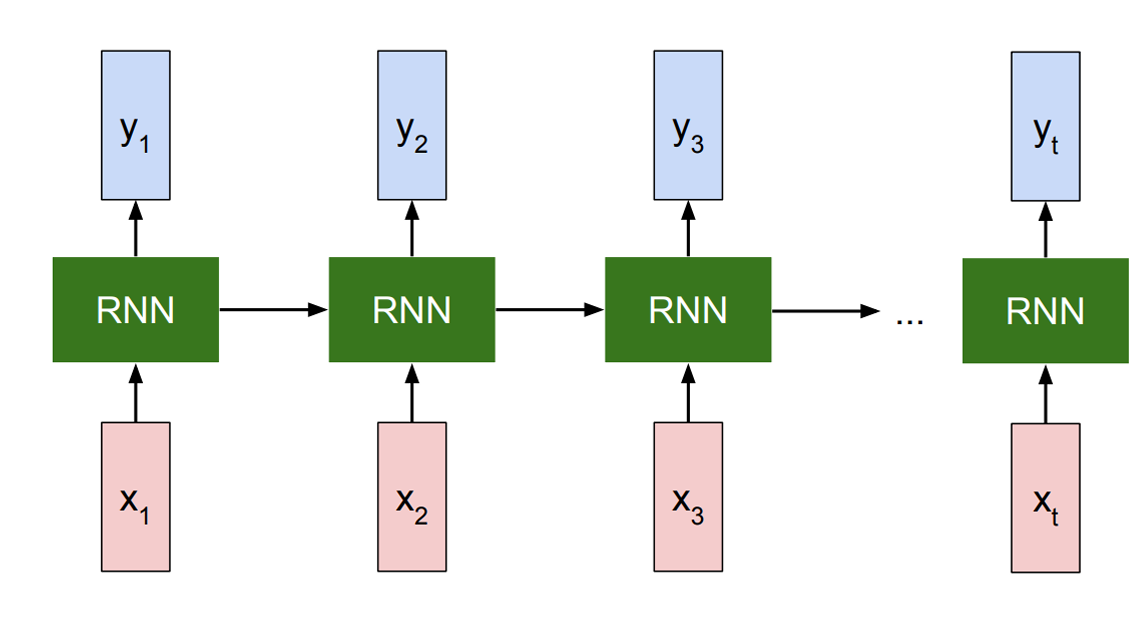
这个图就清楚展示了 x 是不同时刻的输入，y是不同时刻的输出。

2.4 RNN 隐藏状态的更新

RNN 隐藏状态的更新公式为：
h t = f W ( h t − 1 , x t ) h_t=f_W(h_{t-1},x_t) ht=fW(ht−1,xt)，

其中 h 𝑡 ℎ_𝑡 ht表示 new state（新的记忆），当前时间步的 hidden state。
h 𝑡 − 1 ℎ_{𝑡-1} ht−1表示 old state（旧的记忆），上一个时间步的 hidden state。
x 𝑡 x_{𝑡} xt表示 input vector（当前输入），当前时间步的输入向量。
f W f_{W} fW表示带参数的函数，一个可学习的函数，参数是 W W W，在所有时间步共享，也就是每一个时间步，用的都是同一个函数、同一套参数 W W W。

2.5 RNN 的输出

RNN output generation（输出生成） 的公式为：
y t = f W 0 ( h t ) y_t=f_{W_0}(h_{t}) yt=fW0(ht)，

其中 y 𝑡 y_𝑡 yt表示当前时间步的输出。
h 𝑡 ℎ_{𝑡} ht表示 new state（新的 hidden state）。
f W 0 f_{W_0} fW0表示输出函数，另一个可学习函数，参数是 W 0 W_0 W0，在所有时间步共享。

因此现在一个完整的 RNN 在时间维度上全部摊开在这里。

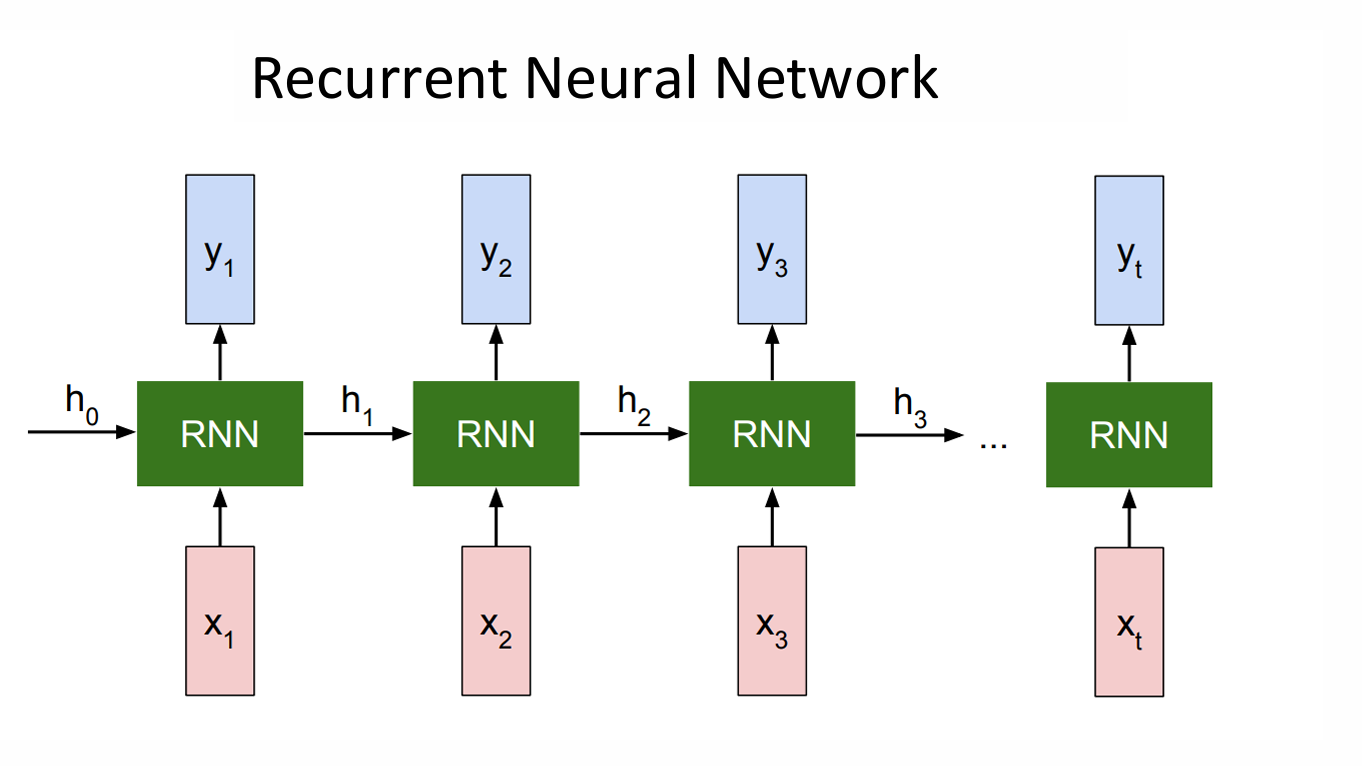
RNN 在处理序列时，会从一个初始隐藏状态 h 0 ℎ_0 h0开始，逐步读入 𝑥 1 , 𝑥 2 , ... 𝑥_1,𝑥_2,... x1,x2,...，并在每个时间步更新 hidden state，同时生成对应的输出 y t y_t yt。

2.6 最基础的 RNN（vanilla RNN / Elman RNN）

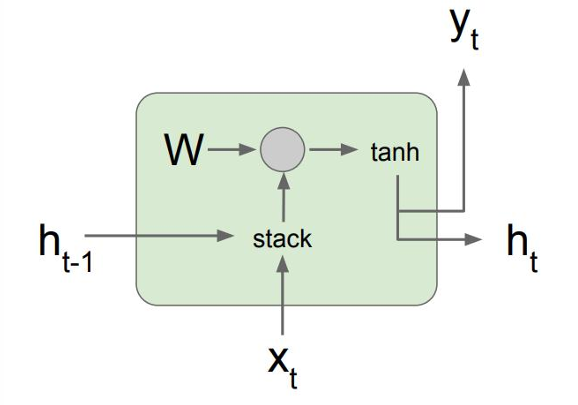
我们现在站是一个最基础的 RNN（vanilla RNN / Elman RNN），它只有一个状态：hidden vector h ℎ h，它在每个时间步由"上一步的 h ℎ h+ 当前输入 𝑥 𝑥 x"通过 t a n h tanh tanh更新，输出 𝑦 𝑦 y只是对 h ℎ h做一次线性映射。

用公式表示，那就是这里 h t = f W ( h t − 1 , x t ) h_t=f_W(h_{t-1},x_t) ht=fW(ht−1,xt)的学习函数是 h t = tanh ⁡ ( W h h h t − 1 + W x h x t ) h_t = \tanh\left(W_{hh} h_{t-1} + W_{xh} x_t\right) ht=tanh(Whhht−1+Wxhxt)，

输出生成公式为 y t = W h y h t y_t = W_{hy} h_t yt=Whyht，这里学习函数就如前面所说是简单的一次线性映射。

我们下面用展开的方式一步步是怎么计算的。
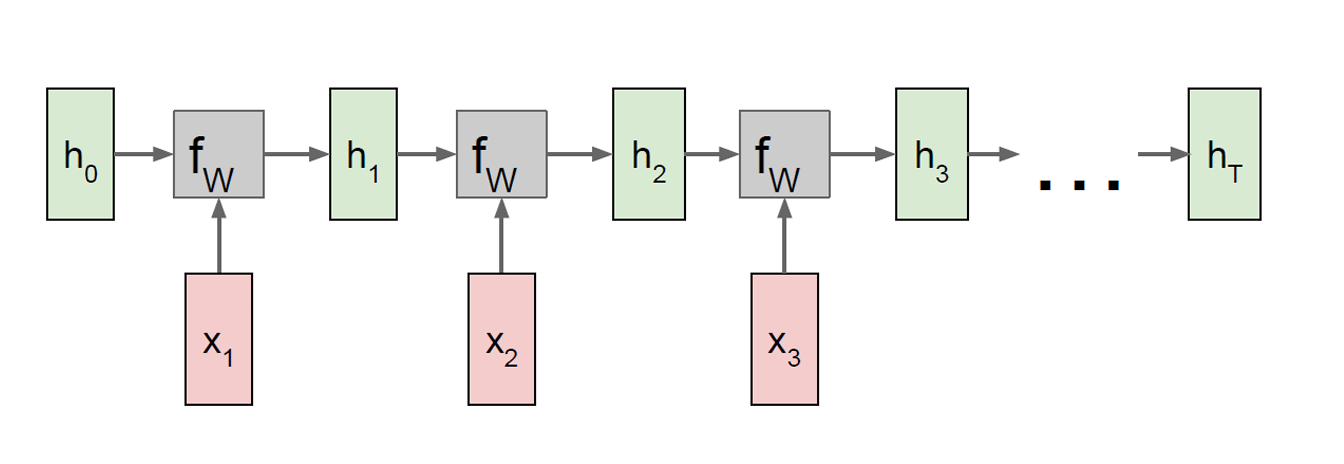从左边开始，如下图所示是一步。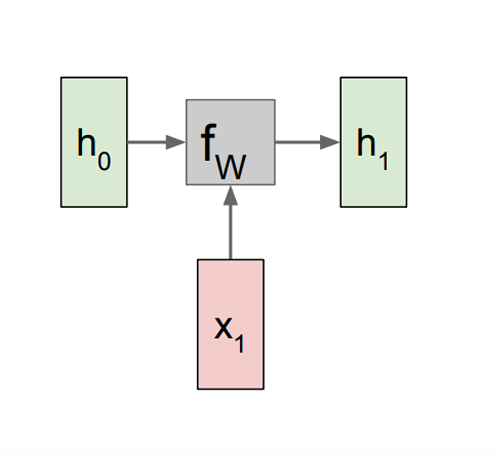
h 1 = f W ( h 0 , x 1 ) h_1 = f_W(h_0, x_1) h1=fW(h0,x1)，

其中 h 0 h_0 h0是初始 hidden state（通常初始化为 0 向量，或设为可学习参数）
x 1 x_1 x1是第一个时间步的输入向量（例如第一个词的 embedding）
f W f_W fW是带参数 W W W 的递推函数（RNN 单元本身，在所有时间步共享参数）
h 1 h_1 h1是更新后的 hidden state，表示在看到 x 1 x_1 x1 之后模型的内部记忆状态

最上面的那张图正沿着这样的步骤，一步一步接着进行下去，这里每一步都是一样的 f W f_W fW，也就是参数共享（re-use the same weight matrix）。

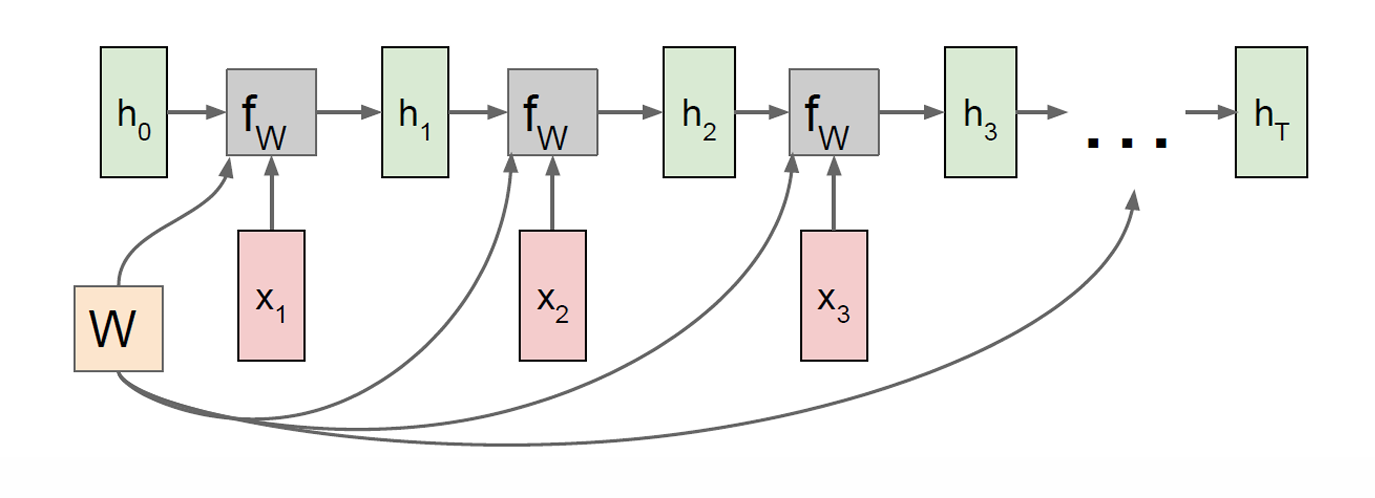
2.7 结构拓展

我们将之与前面说的不同结构相结合。

首先是 many-to-many（多对多），在每个时间步同时读一个输入 x t x_t xt，并产生一个输出 y t y_t yt，输出与输入在时间上对齐。

因此现在每个状态更新的同时都会带有一个新的输出。

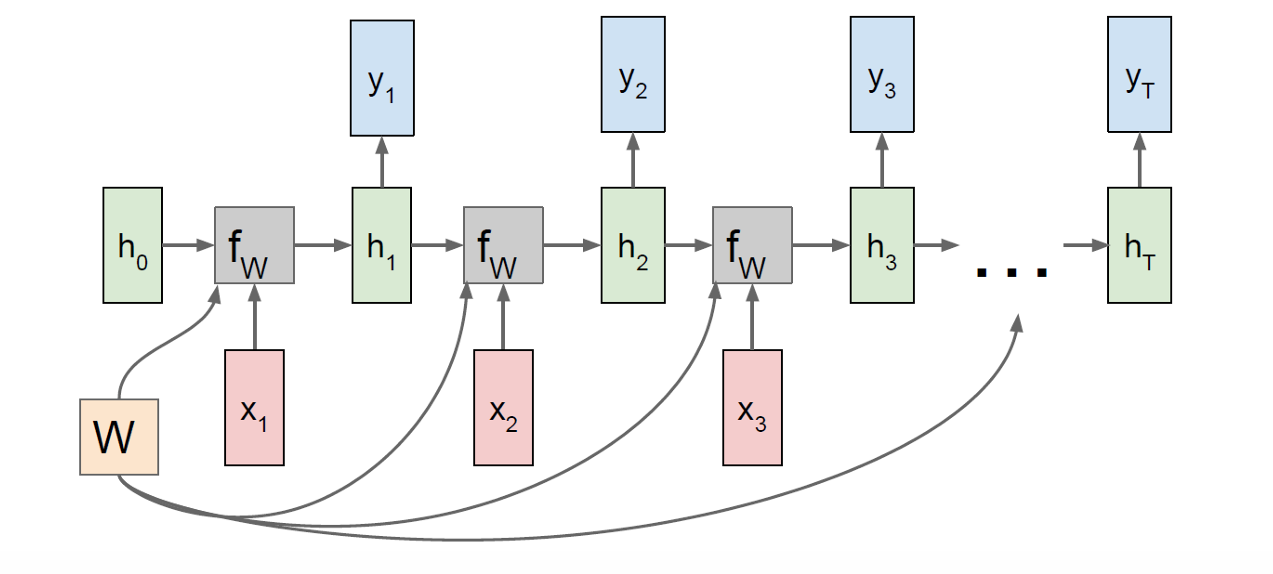
因此我们可以计算每一步的损失函数Loss。

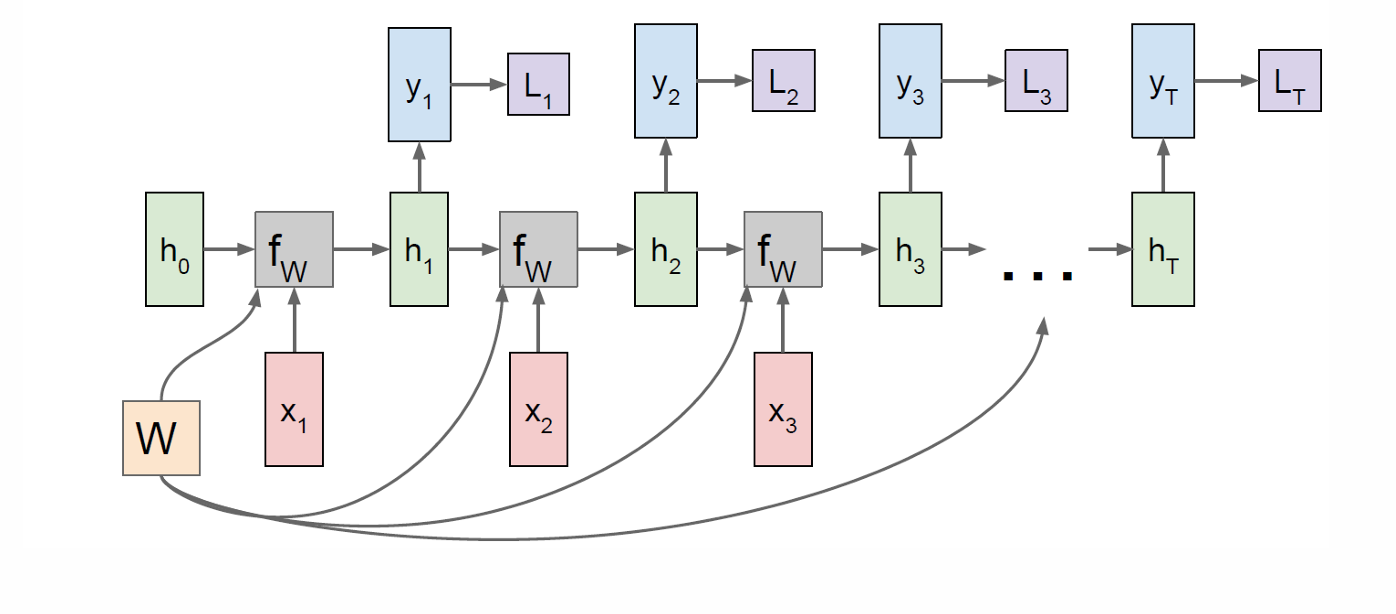
我们现在将其损失函数加起来就得到总损失。

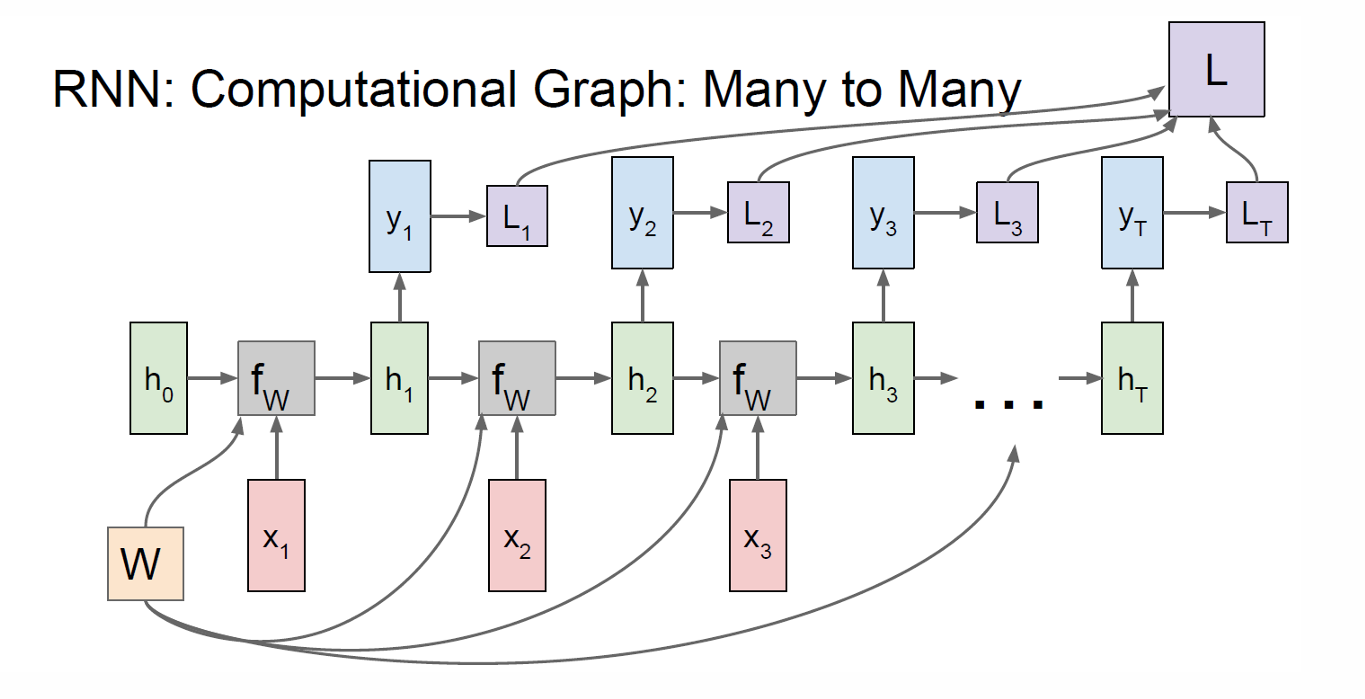
many-to-on（多对一），输入是一整段序列，但只在最后一个时间步产生一个输出。

one-to-many（一对多），RNN 从一个初始信息（如一个向量或起始符）开始，通过时间递推，逐步生成多个输出。

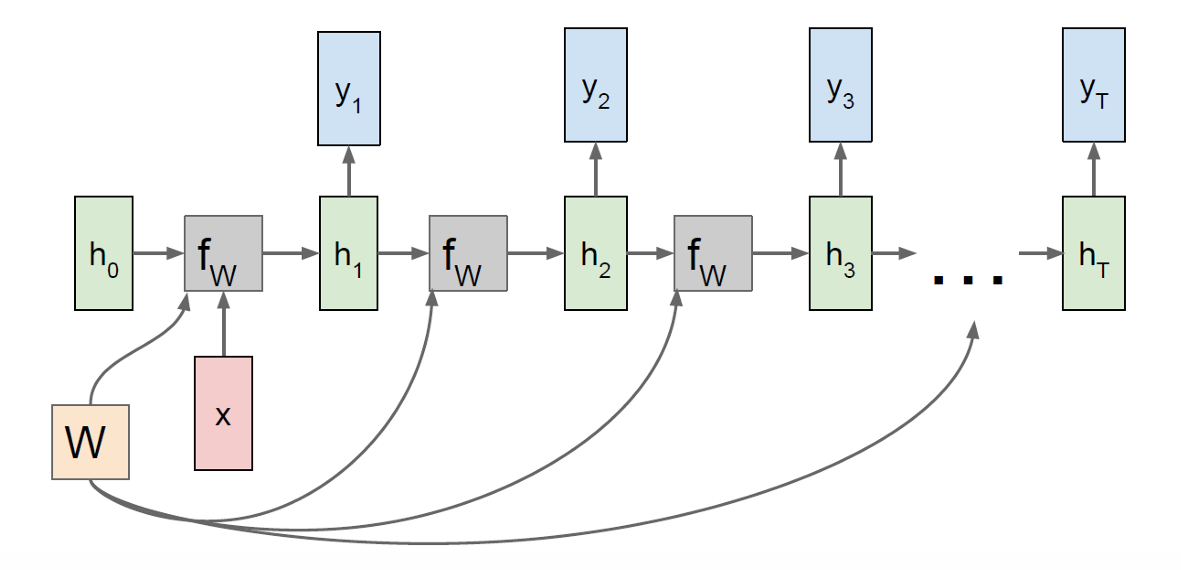
2.7.1 Sequence-to-Sequence（Seq2Seq）模型

Sequence-to-Sequence模型是将两个 RNN 结构拼在一起。

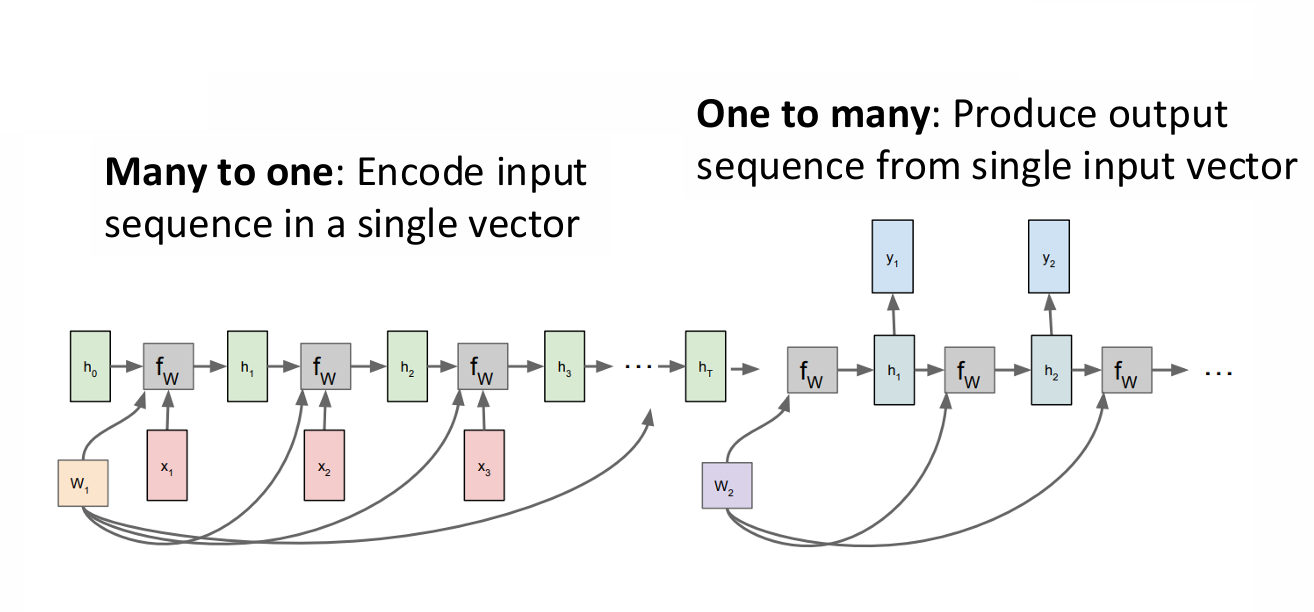
模型先把输入序列编码成一个向量（Encoder），再从这个向量出发生成一个输出序列（Decoder）。

左半部分：Many-to-one（Encoder，编码器）。

右半部分：One-to-many（Decoder，解码器）。

2.8 RNN应用

我们用一个例子展示 RNN 如何做字符级语言模型（Character-level Language Model）。

假设我们训练的序列是"hello"，这里我们涉及4个字符分别是"h,e,l,o"，这四个字符我们使用One-Hot 编码（独热编码），将每个字符表示为一个长度等于词表大小的向量，其中只有一个位置是 1，其余全是 0。

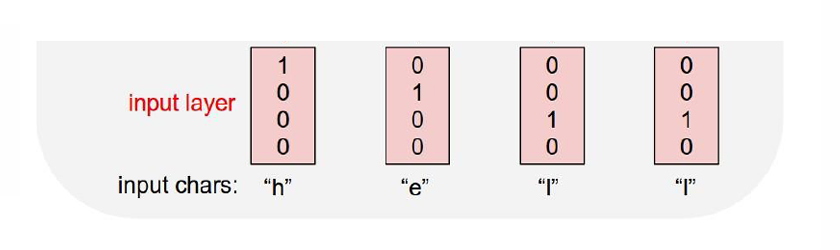
我们可以根据公式进行计算。

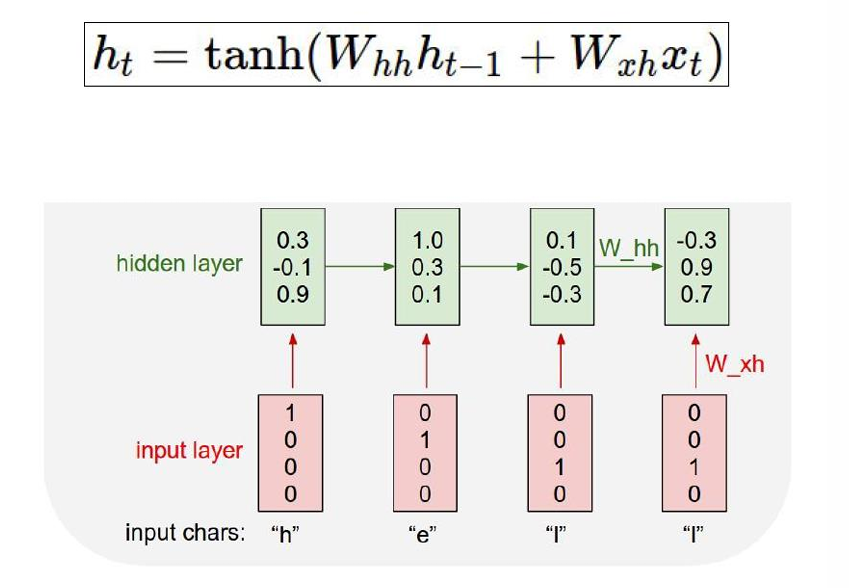
如图所示，红色表示的是输入 (x_t)（one-hot 编码的字符）

第一个绿色是初始隐藏状态 h 0 h_0 h0， 后面的绿色依次是 h 1 , h 2 , ... h_1, h_2, \ldots h1,h2,...。

在计算新的隐藏状态使用的参数用于之前隐藏状态的参数是 W h h W_{hh} Whh，用于输入的参数是 w x h w_{xh} wxh。

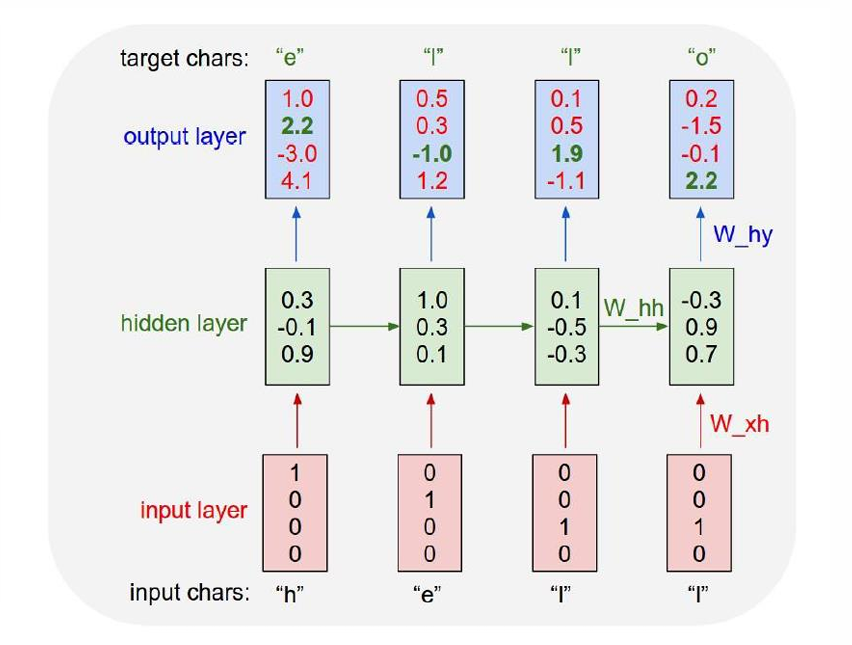
蓝色是由当前隐藏状态 h t h_t ht计算得到的输出 y t y_t yt，所以这里的参数是 W h y W_{hy} Why。

整个模型是many-to-many（多对多）。

我们在实际应用中还会使用Softmax函数将logits转成概率分布，如下图所示。

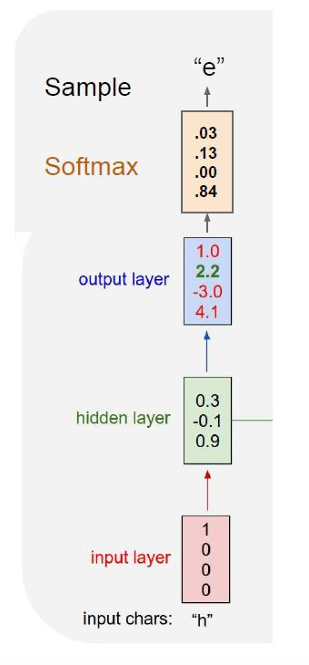
在测试阶段，模型一次只生成（采样）一个字符，并把刚生成的字符再喂回模型作为输入。

因此完整过程如下。

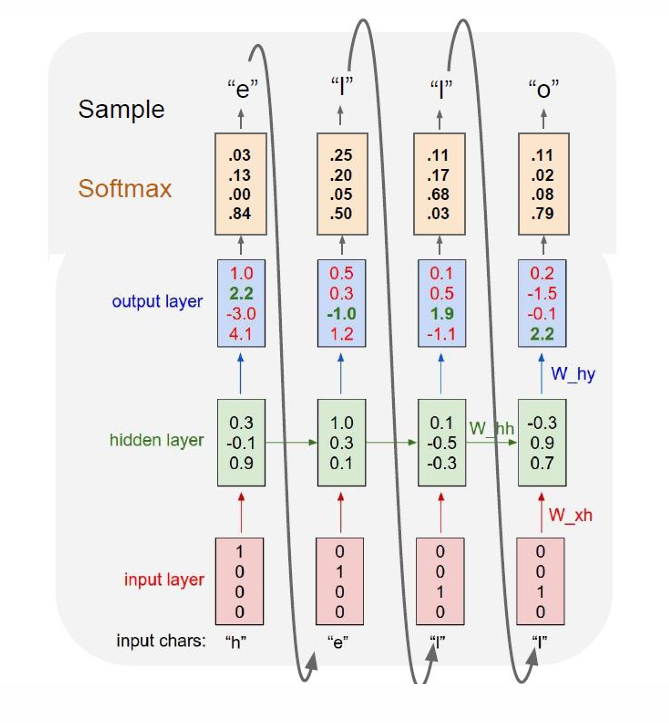
因此我们可以看出字符级语言模型是在每一个时间步，根据当前字符和之前的上下文，预测"下一个字符"的概率分布。

所以我们现在分开理解，我们如果要输入hello这个单词，我们输入h后，模型就会根据输入h，预测我们下一个输入e，然后它会将这个预测结果再喂给自己，得出下一个预测l，从而得到完整的预测hello。

2.9 RNN的训练方式

RNN的训练方式是时间反向传播（Backpropagation Through Time，BPTT）。

我们先沿时间顺序 forward 跑完整个序列，算出所有输出和总 loss，再沿时间反方向 backward，反方向传播计算梯度来更新共享参数，这个过程就叫时间反向传播（Backpropagation Through Time，BPTT）。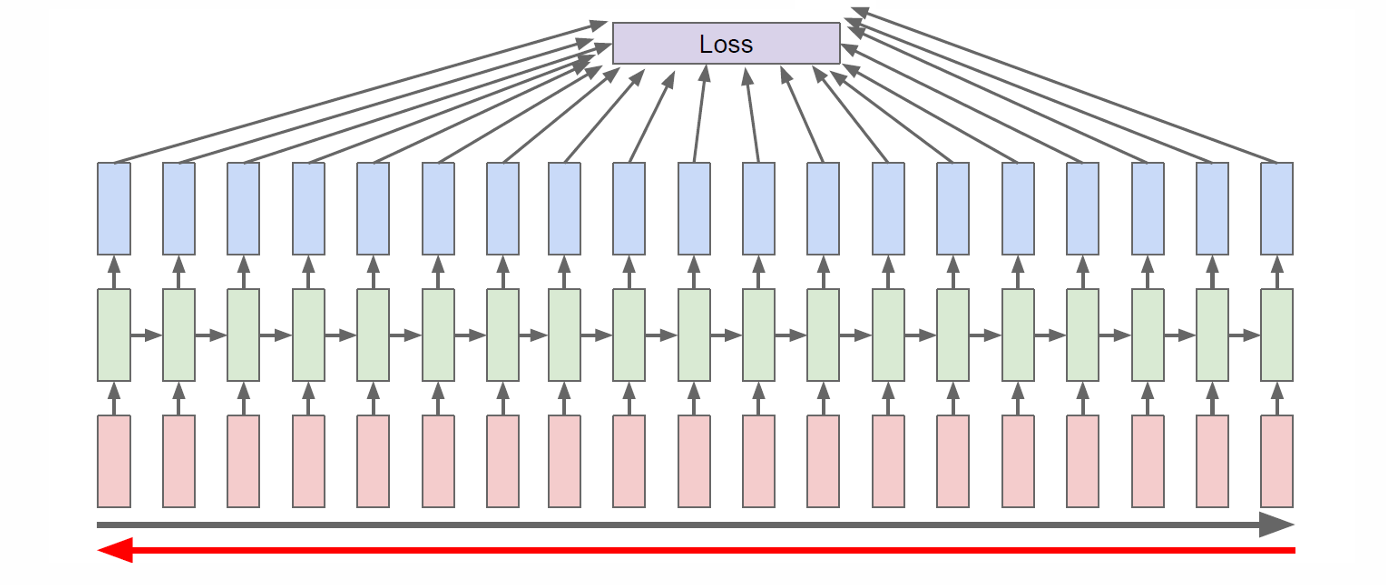

那么为什么不能一步一步算、一步一步更新？

因为RNN的参数在所有时间步共享，所以无法中途修改。

2.9.1 截断时间反向传播（Truncated Backpropagation Through Time，TBPTT）

如果我们按照前面的方法把序列完全展开，梯度从最后一步一路传回最开始会遇到以下几个问题：

• 内存需求极大
• 计算非常慢
• 梯度消失严重

因此在实际训练中我们一般使用TBPTT，将很长的序列切成一小段一小段（chunks），每次只在这段里做 forward + backward，而不是在整个序列上反向传播。

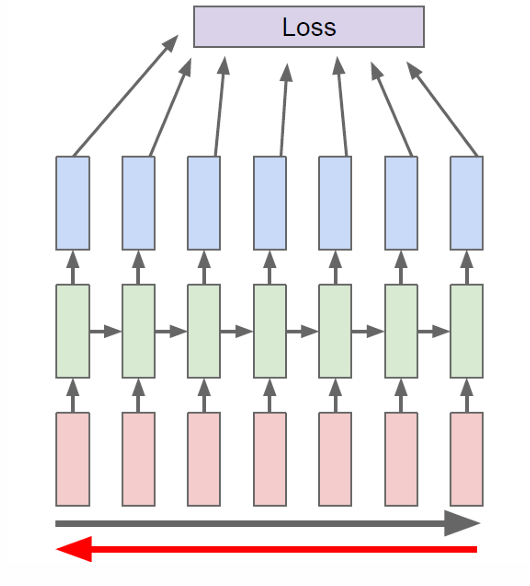
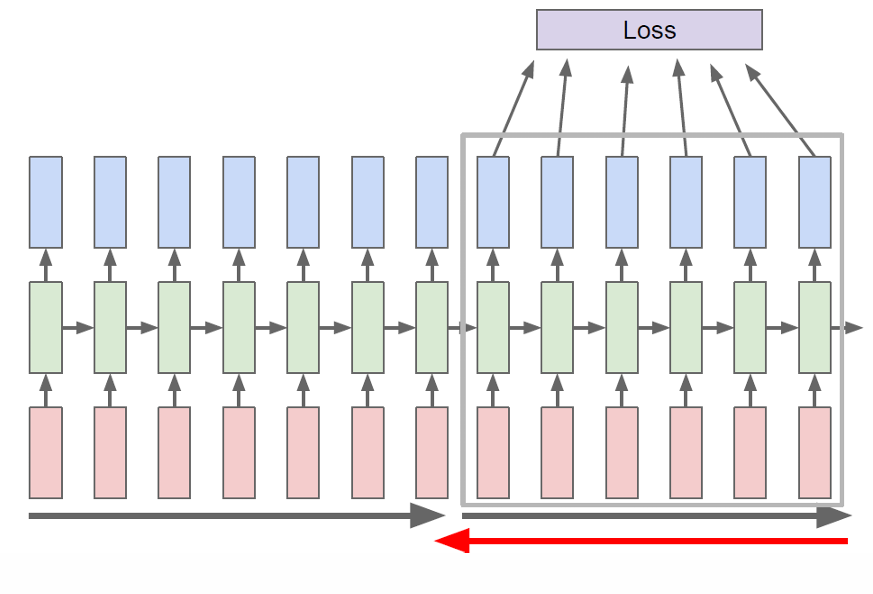
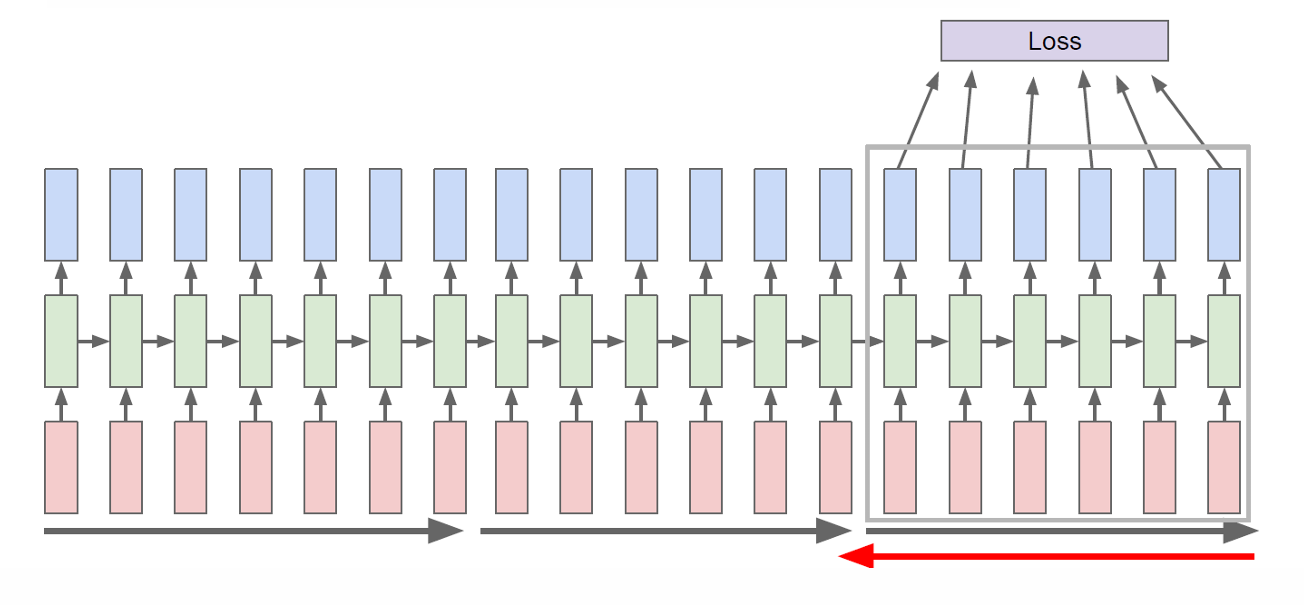
hidden state 一直往前传（不截断，如灰色箭头所示），但梯度只往回传固定的 K K K个时间步（被截断，如红色箭头所示）。

2.10 RNN 总结

RNN 的优点有：

1. 可以处理任意长度的输入序列。RNN 结构不变，只是时间步变多。换句话说那就是RNN非常适合处理序列数据（文本、语音、时间序列）
2. 在"理论上"，第 t 步的计算可以利用很久以前的信息。
3. 输入变长，模型参数不会变多。这一点与第一点同理，因为权重矩阵 W x h W_{xh} Wxh， W h h W_{hh} Whh， W h y W_{hy} Why是固定的，不会因为序列更长就多参数。
4. 每个时间步用的是同一套权重，这带来一种时间上的对称性（symmetry）。

RNN 的缺点有：

1. 递归计算很慢。RNN不能并行，后面的时间步必须等前面的算完，因此对 GPU 非常不友好。序列一长，训练就慢。
2. 在实际中，很难真的利用很久以前的信息。这是因为梯度消失，即使 hidden state 理论上传得下去，但训练时早期信息影响会越来越弱，模型更关注"最近几步"。

2.11 更多应用

2.11.1 图像字幕生成（Image Captioning）模型

本质是CNN + RNN 的 sequence-to-sequence 结构。

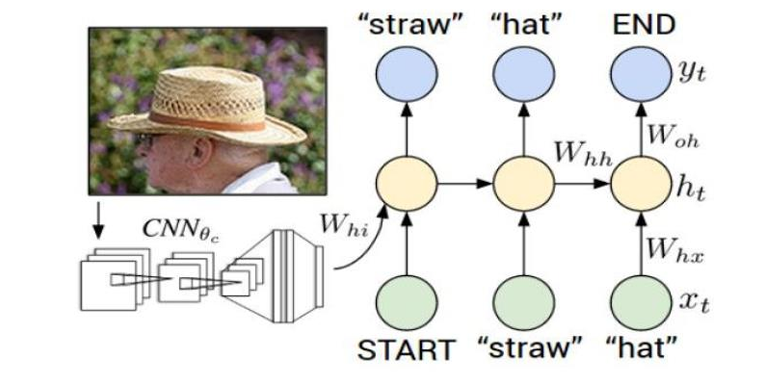
我们输入一张图片，CNN（卷积神经网络）逐层提取特征，最终输出一个固定长度的向量，它不是一个我们可以理解的文字信息，而是描述这张图的语义的数学表示。

而后面的 RNN 会把图像特征"翻译"成一句话。这里输出的图像特征通过权重 W h i W_{hi} Whi送进 RNN 的 hidden state,RNN 在生成每一个词的时候，脑子里一直带着这张图片的信息。

再细化一点，那就是 RNN 内部第 t t t个时间步：输入上一个词后，计算新的 hidden state h t h_t ht，然后输出一个词的概率分布 y t y_t yt， 选一个词作为当前输出，然后这个输出继续作为输入生成下一个词。这与前面说的字符级语言模型（Character-level Language Model）是类似的。

因此现在我们的 hidden state 的更新公式升级为：
h t = tanh ⁡ ( W x h x t + W h h h t − 1 + W i h v ) h_t = \tanh\left(W_{xh} x_t+ W_{hh} h_{t-1}+ W_{ih} v\right) ht=tanh(Wxhxt+Whhht−1+Wihv)

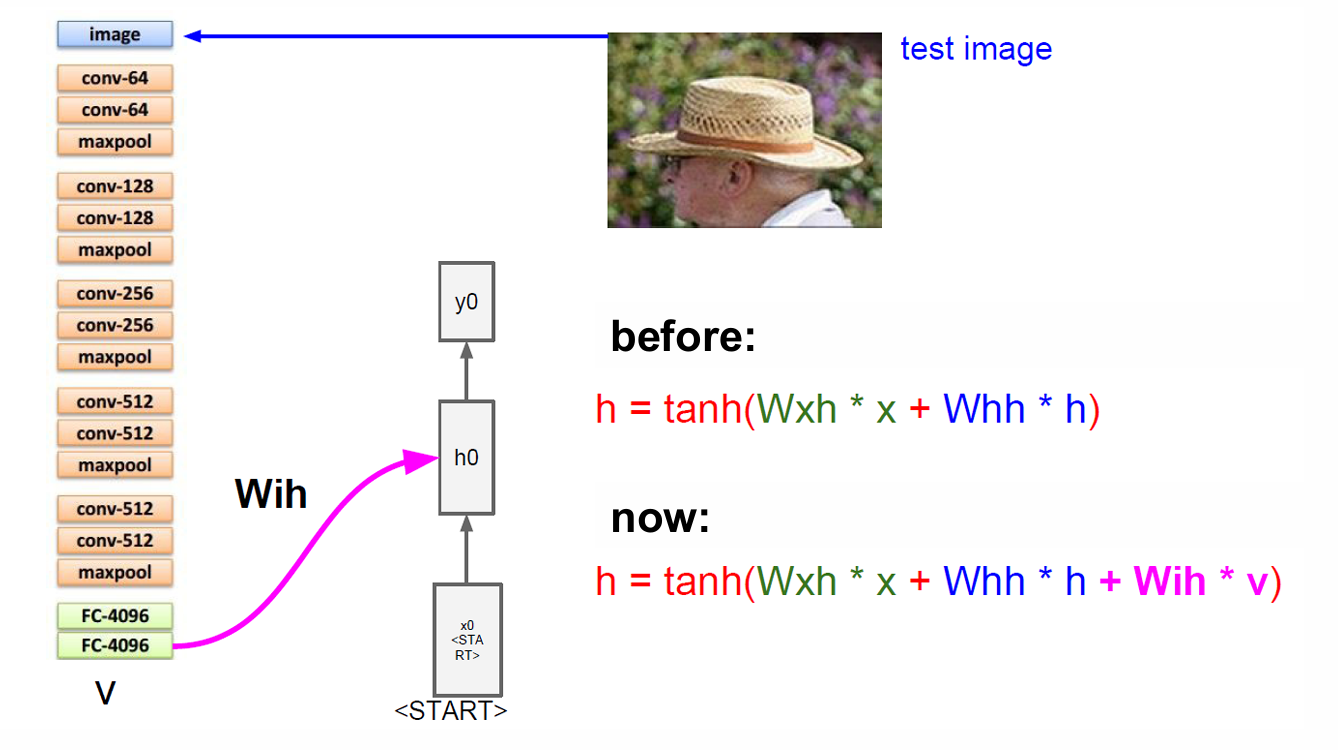
因此在这个例子中，我们放入一个草帽的照片。

我们的 CNN 提取图片的信息，将这个输入给 RNN 其采样生成第一个词"straw"。

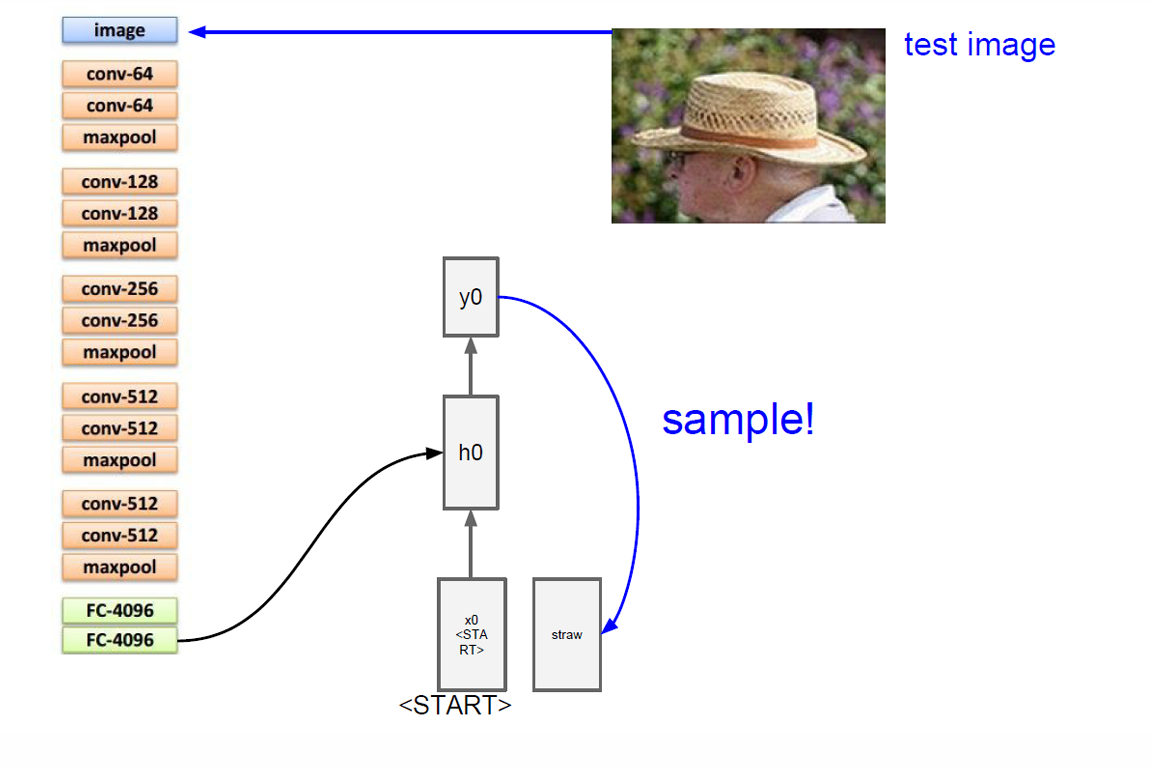
然后这个词作为下一步的输入然后更新隐藏状态并且得到新的输出"hat"。

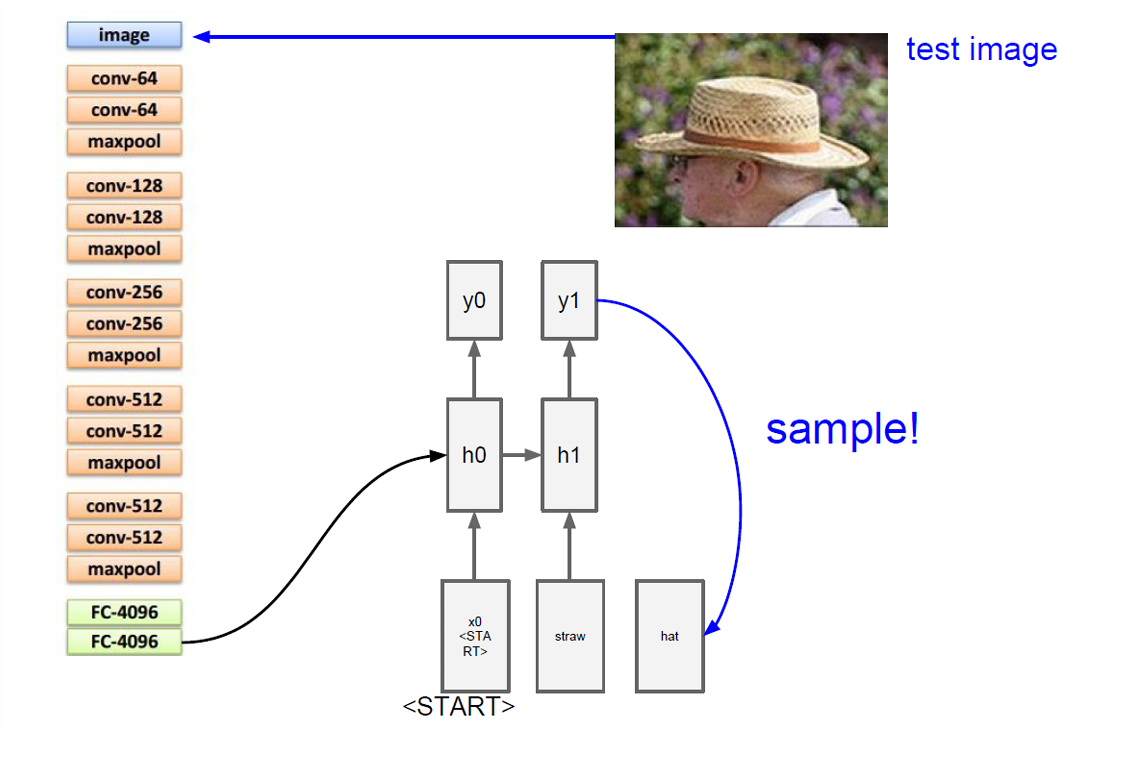
这就是图像字幕生成模型。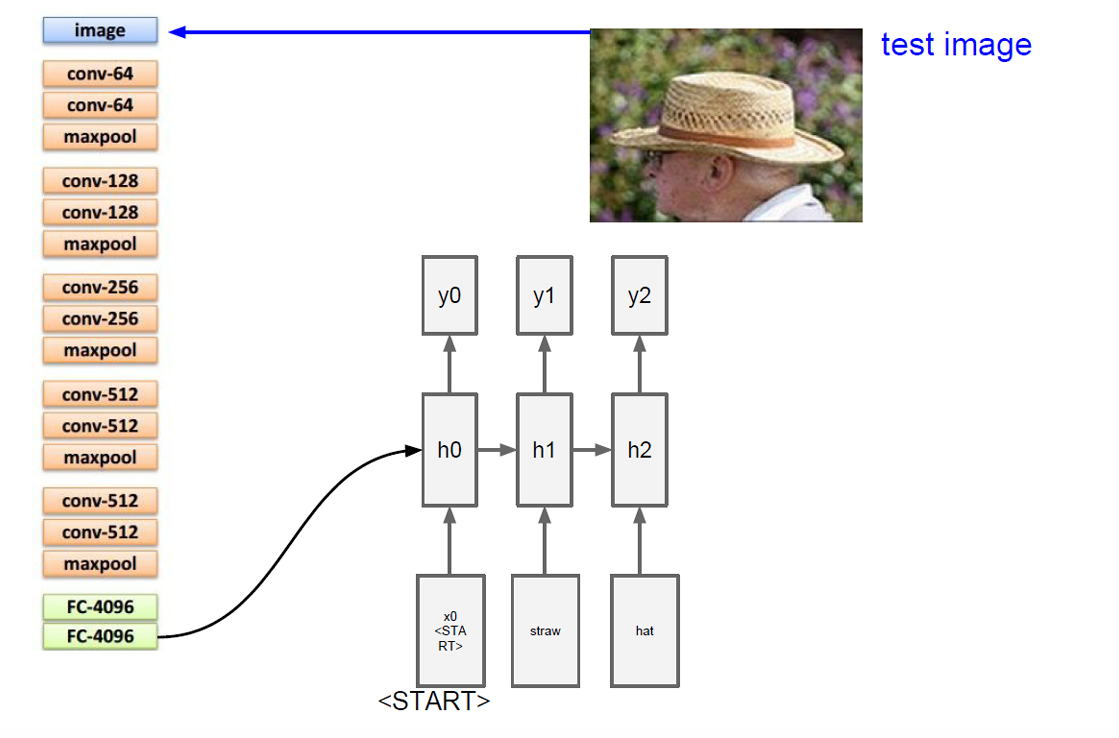

下面展示更多例子。

当然也会存在一些问题，下面就展示一些失败的例子。

所以即使模型能生成"看起来很合理的句子"，也经常会在语义理解上出错。

2.11.2 带注意力机制的图像描述（Image Captioning with Attention）

我们前面提到了一些失败案例。这里说的注意力机制正是用于解决这类问题的。我们让 RNN 在生成每一个单词时，把注意力集中在图像的不同空间位置上。

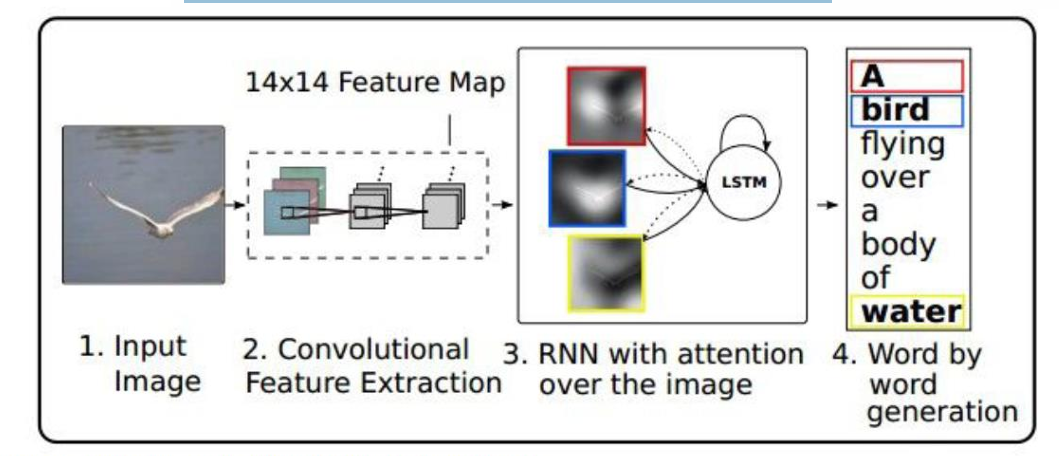
在原来的RNN中，我们一次看一张图，将整个图压成一个向量，后面生成所有词都靠"记忆"。

现在有注意力机制，RNN每生成一个词，我们再决定看向图的哪里，因此会看图片多次。

所以现在我们的 CNN 不再只输出一个向量，而是输出一组空间特征。

我们的 RNN 也不会只看一个位置而是对所有 L L L个空间位置给一个概率，也就是一个 attention 向量。

然后我们把把整张图"按注意力权重压缩"为一个向量。

当前生成这个词时，图像中哪些地方最重要，就占比更大。

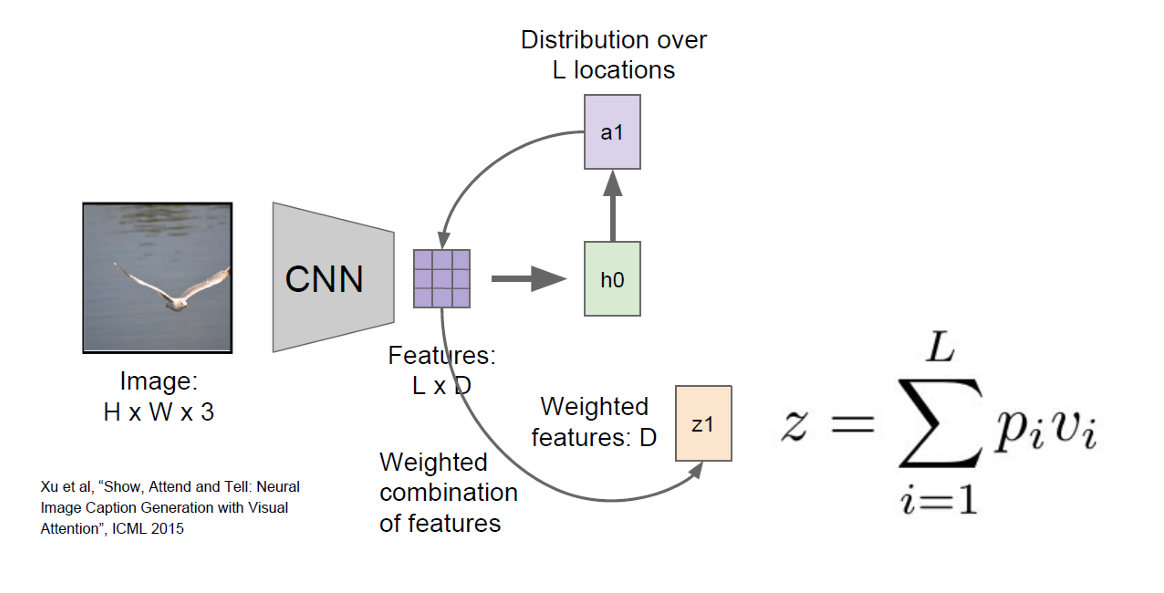
这里因为我们是第一个所以我们的第一个上下文向量计算为 z 1 = ∑ i = 1 L α 1 , i   v i z_1=\sum_{i=1}^{L} \alpha_{1,i} \, v_i z1=∑i=1Lα1,ivi，其中 v i v_i vi是第 i i i个空间位置的 CNN 特征向量， α 1 , i \alpha_{1,i} α1,i是在生成第一个词时，对第 i i i个位置的注意力权重。

我们先更新 hidden state，
h 1 = R N N ( h 0 , y 0 , z 1 ) h_1 = \mathrm{RNN}(h_0, y_0, z_1) h1=RNN(h0,y0,z1)。

其中 h 0 h_0 h0是初始 hidden state 。
y 0 y_0 y0是起始词的嵌入向量。
z 1 z_1 z1是由 attention 机制得到的图像上下文向量。

由 hidden state 生成输出分布
d 1 = S o f t m a x ( W h y   h 1 ) d_1 = \mathrm{Softmax}(W_{hy} \, h_1) d1=Softmax(Whyh1)。

我们再从 d 1 d_1 d1里采样或取最大概率词，得到第一个词 y 1 y_1 y1。

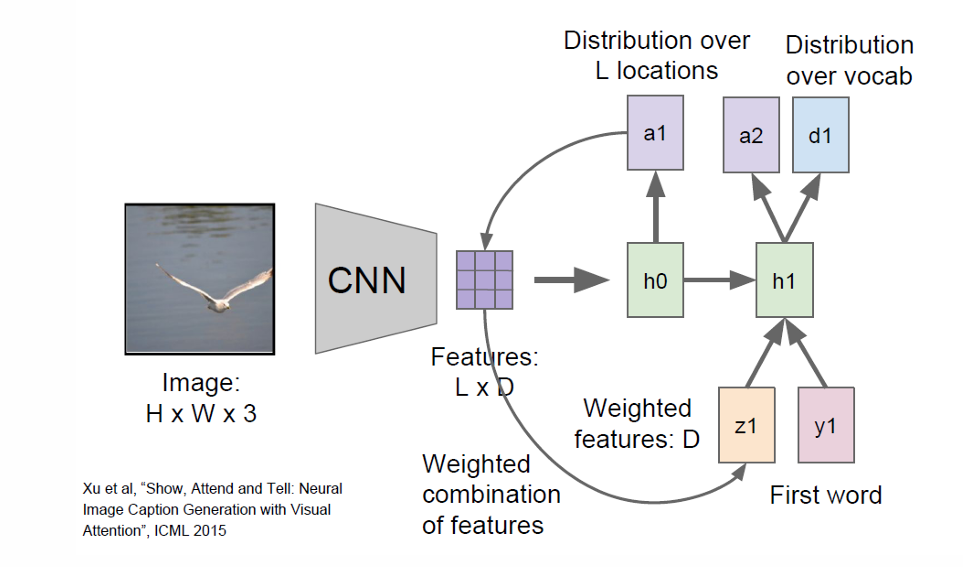
我们还可以根据这里的 h 1 h_1 h1计算出新的第二个词的注意力权重 a 2 a_2 a2，由此计算出第二个上下文向量 z 2 z_2 z2，然后结合第一个得到的词更新 h 2 h_2 h2，由此往下。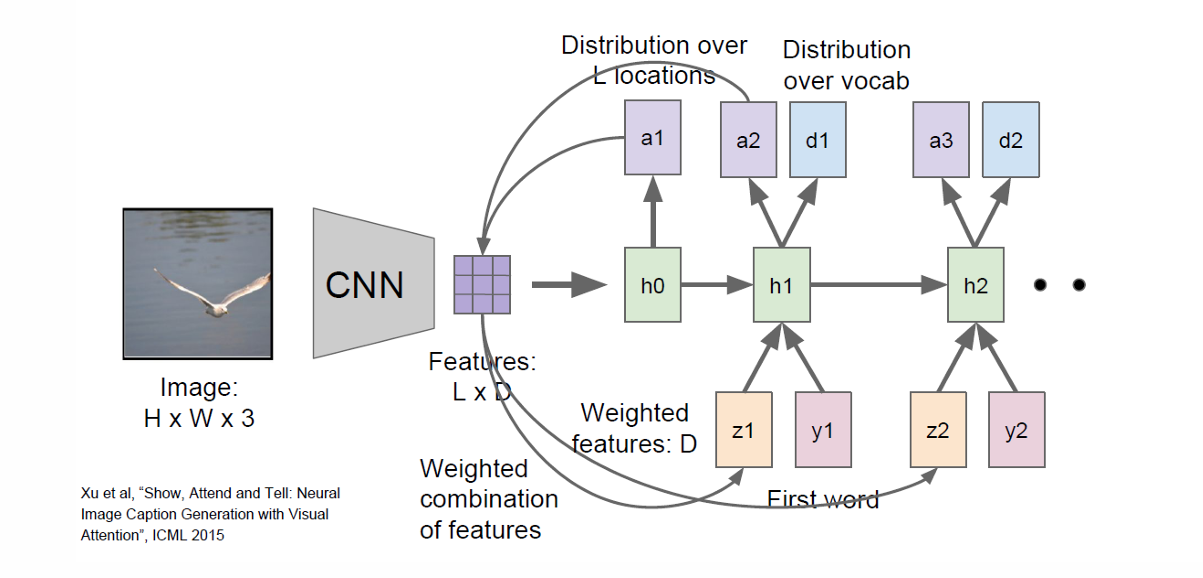

整个过程如下图所示。

这里 Soft Attention（软注意力）是模糊地看一片区域。

而 Hard Attention（硬注意力）是只看一个位置，其它地方完全不看。

下面展示一些结果。

3. LSTM（Long Short-Term Memory，长短期记忆网络）

我们现在介绍一种更有记忆的网络LSTM。

我们前面可以注意到，很多图里用的并非RNN而是LSTM，因为 Vanilla RNN 将所有信息压缩进同一个 h t h_t ht中，时间一长，旧信息会被不断覆盖，而且反向传播时梯度容易消失。

3.1 梯度消失

我们现在解释为什么会梯度消失？

首先 h t = tanh ⁡ ( W h h h t − 1 + W x h x t ) h_t = \tanh\left(W_{hh} h_{t-1} + W_{xh} x_t\right) ht=tanh(Whhht−1+Wxhxt)

我们用矩阵写法，那就是 h t = tanh ⁡ ( ( W h h W h x ) ( h t − 1 x t ) ) h_t = \tanh \left( \begin{pmatrix} W_{hh} & W_{hx} \end{pmatrix} \begin{pmatrix} h_{t-1} \\ x_t \end{pmatrix} \right) ht=tanh((WhhWhx)(ht−1xt))

也就是 h t = tanh ⁡ ( W ( h t − 1 x t ) ) ) h_t = \tanh \left( W \begin{pmatrix} h_{t-1} \\ x_t \end{pmatrix} \right) ) ht=tanh(W(ht−1xt)))

我们现在开始反向传播。

反向传播过程中，梯度需要乘以权重矩阵 W h h W_{hh} Whh的转置（即 W h h T W_{hh}^T WhhT）

从 h t h_t ht到 h t − 1 h_{t-1} ht−1梯度为 ∂ h t ∂ h t − 1 = tanh ⁡ ′ ( W h h h t − 1 + W x h x t ) W h h \frac{\partial h_t}{\partial h_{t-1}} = \tanh'(W_{hh}h_{t-1} + W_{xh}x_t)W_{hh} ∂ht−1∂ht=tanh′(Whhht−1+Wxhxt)Whh

我们现在展示一个标准的循环神经网络（Vanilla RNN）中梯度的传播过程，这里包含多个时间步，每个时间步都有一个RNN单元。

损失函数 L L L对权重 W W W的梯度为 ∂ L ∂ W = ∑ t = 1 T ∂ L t ∂ W \frac{\partial L}{\partial W} = \sum_{t=1}^{T} \frac{\partial L_t}{\partial W} ∂W∂L=∑t=1T∂W∂Lt

因此 ∂ L T ∂ W = ∂ L T ∂ h T ∂ h T ∂ h T − 1 ⋯ ∂ h 1 ∂ W \frac{\partial L_T}{\partial W} = \frac{\partial L_T}{\partial h_T} \frac{\partial h_T}{\partial h_{T-1}} \cdots \frac{\partial h_1}{\partial W} ∂W∂LT=∂hT∂LT∂hT−1∂hT⋯∂W∂h1
= ∂ L T ∂ h T ( ∏ t = 2 T ∂ h t ∂ h t − 1 ) ∂ h 1 ∂ W = \frac{\partial L_T}{\partial h_T} \left( \prod_{t=2}^{T} \frac{\partial h_t}{\partial h_{t-1}} \right) \frac{\partial h_1}{\partial W} =∂hT∂LT(∏t=2T∂ht−1∂ht)∂W∂h1

而这里的 ∂ h t ∂ h t − 1 \frac{\partial h_t}{\partial h_{t-1}} ∂ht−1∂ht，计算前面提到过 ∂ h t ∂ h t − 1 = tanh ⁡ ′ ( W h h h t − 1 + W x h x t ) W h h \frac{\partial h_t}{\partial h_{t-1}} = \tanh'(W_{hh}h_{t-1} + W_{xh}x_t)W_{hh} ∂ht−1∂ht=tanh′(Whhht−1+Wxhxt)Whh

由于由于 t a n h tanh tanh激活函数的导数 t a n h ′ tanh' tanh′的值域在 (0,1) 之间，因此当这个导数多次相乘时，结果会接近于0，导致梯度消失。

3.2 LSTM 的结构

LSTM 与 RNN 相比，在每个时间步不仅计算 h t h_t ht，它还同时维护一个"记忆通道" c t c_t ct，叫做cell state（细胞状态）。
c t c_t ct用四个门（i, f, o, g）进行控制。

门	名字	作用	数值范围
( i t i_t it)	Input gate	写不写新信息	(0, 1)
( f t f_t ft)	Forget gate	忘不忘旧记忆	(0, 1)
( o t o_t ot)	Output gate	输出多少记忆	(0, 1)
( g t g_t gt)	Candidate	新候选内容	(-1, 1)

计算公式如下：

i t f t o t g t \] = \[ σ σ σ tanh ⁡ \] ( W \[ h t − 1 x t \] ) \\begin{bmatrix} i_t \\\\ f_t \\\\ o_t \\\\ g_t \\end{bmatrix}= \\begin{bmatrix} \\sigma \\\\ \\sigma \\\\ \\sigma \\\\ \\tanh \\end{bmatrix} \\left( W \\begin{bmatrix} h_{t-1} \\\\ x_t \\end{bmatrix} \\right) itftotgt = σσσtanh (W\[ht−1xt\]) 作为关键核心的细胞状态 c t c_t ct的更新公式为： c t = f t ⊙ c t − 1 + i t ⊙ g t c_t = f_t \\odot c_{t-1} + i_t \\odot g_t ct=ft⊙ct−1+it⊙gt 其中 ⊙ \\odot ⊙表示元素乘法（Hadamard乘积）。 隐藏状态的更新公式为： h t = o t ⊙ tanh ⁡ ( c t ) h_t = o_t \\odot \\tanh(c_t) ht=ot⊙tanh(ct) 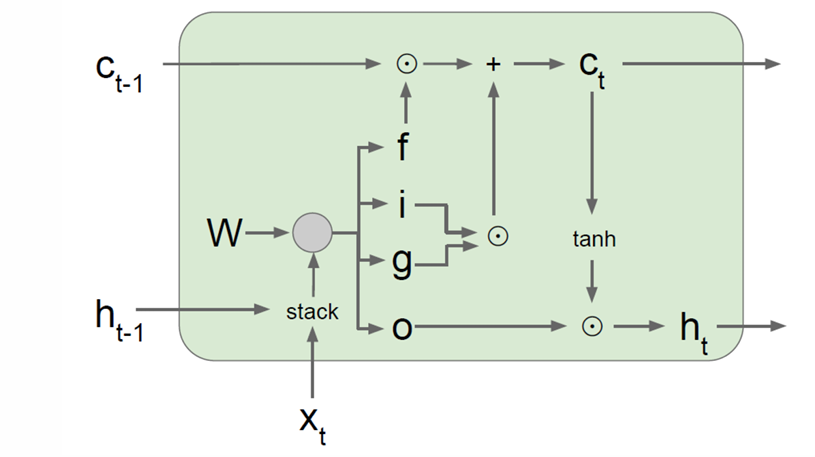 因此整个大权重矩阵的维度是 4 h × 2 h 4h×2h 4h×2h。因为四个门是 4 h 4h 4h，而输入是 2 h 2h 2h包含上一时刻隐藏状态和当前输入，将它们拼接在一起。 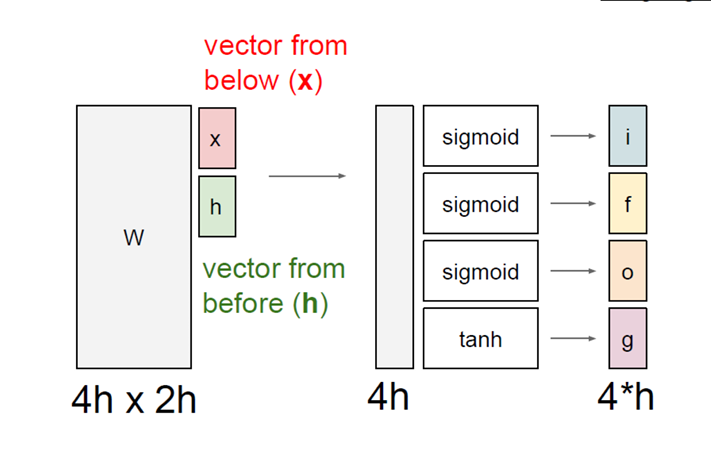 ## 4. MLLMs（Multimodal Large Language Models，多模态大语言模型） 我们现在常见的GPT，Gemini之类的都是多模态大语言模型，它们都是以Transformer为核心的系统。 它使用 Vit 把一张图片切成很多"patch token"，像一句话的 token 一样，送进 Transformer Encoder，用 Attention 建模全局关系，用 FFN 做非线性变换，最后用一个 \[CLS\] token 做分类。 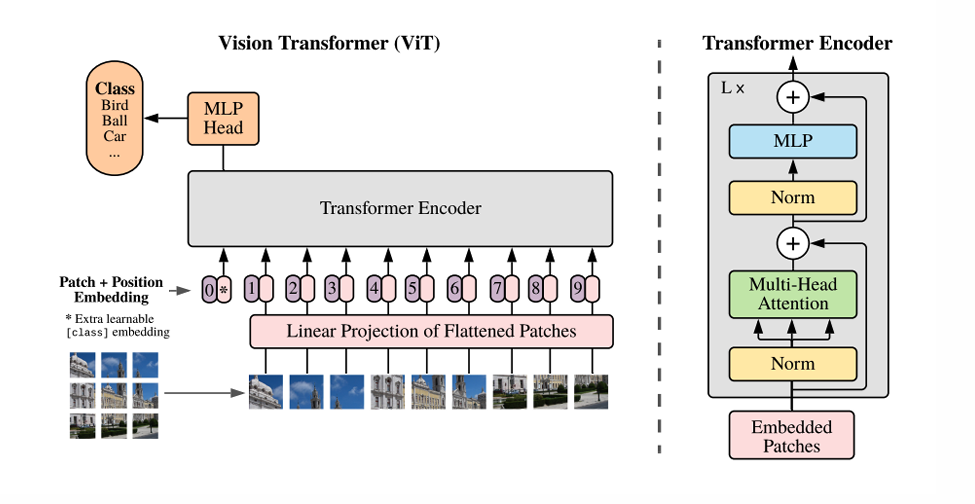 这里 Vit 就是 Transformer Encoder， 是视觉编码器，与传统 CNN 不同，它一上来就有全局视野（self-attention）。