++都是我自己的答案,不一定正确,仅供参考++
1.A:和B:
,这两个分别表示什么,哪个价值更高,为什么?
前一个表示渐进上界,后一个表示渐进下界
我写的前一个价值更高,因为我们更习惯考虑时间开销的上限来判断一个算法的可行性(前一个使用多一点)
2.分治法和动态规划的异同?为什么有些不能使用动规但是能使用分治?
我是这么回答的:
相同:都需要分解成子问题,都可以用来解决最优问题;
异:分治法的子问题相互独立互不重叠,动规的子问题有重叠;分治法自上而下递归,需要合并子问题,而动规自底向上计算,不需要合并子问题:分治法分治法不存储子问题的解,动规需要存储子问题。
为什么有些不能用动规可以用分治:因为有些问题不具备最优子结构和重叠子问题;或者有些问题不需要求最优解,这时候使用分治法
3.限界函数为什么重要?好的限界函数应该具备什么性质?
我的回答:
如果没有限界函数,往往需要遍历所有解空间数,可能达到指数或者阶乘级别,因此需要使用限界函数避免一些无效的搜索,减少时间开销。
性质:1.需要能够快速排除较多的无效探索,2.计算开销不能过大,否则会导致时间开销更多
4.使用分治法求解数组的最大连续和问题
这题最佳方法是动态规划,但是题目要求使用分治,我的写法:
首先可以分成三个部分:左,右,跨越左右
左右都可以直接使用递归实现
跨越左右的部分我是采用了双指针贪心法:先固定左指针在左边最右的位置,右指针在右边最左的位置,每次比较左右较大值,较大的一方加入sum,然后将指针朝边缘移动,并且比较sum和cross_max,使得cross_max最大。
最终返回max(left_max,right_max,cross_max)
5.给定一个m×n的二维数组grid,每个元素都是一个数字,然后计算从(0,0)到(m-1,n-1)的最小值(每次只能向右和向下,路过的位置加入到sum中)
这题是经典的动态规划,可以列出状态转移方程:
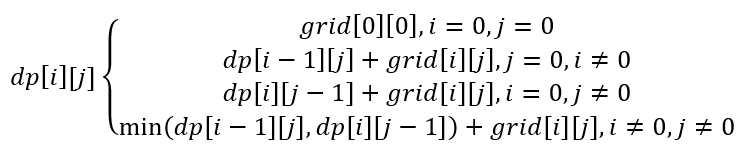
6.一辆车从起点出发,每次加油后可以行驶k公里,每两个加油站的距离保存在x数组中,问最少要加多少次油
贪心算法,每次直到油不够跑到下一个加油站的时候才加油
7.给定一个m×n的二维字符数组board,给定目标word(一维数组),要求从board中选择一个起点,每次可以朝周围四个方向选择,要求最终能按word的顺序遍历,并且不能重复使用已经使用的字符(位置)
使用回溯法,我的思路如下(给出伪代码):
cpp
bool backtrace(char **board,char *word,int n,int m,int i ,int j,int k,bool *visit){
if(k == word.size()) return true;
int grid = {{1,0},{-1,0},{0,-1},{0,1}};
for(int d = 0; d < 4; d++){
ni = i + grid[d][0];
nj = j + grid[d][1];
if(ni < 0 || ni >=n || nj < 0 || nj >= m) continue;
if(board[ni][nj] == word[k] && !visit[ni][nj]){
k++;
visit[ni][nj] = true;
if(backtrace(board,word,n,m,ni,nj,k,visit)) return true;
visit[ni][nj] = false;
k--;
}
}
return false;
}
int main(){
for(int i = 0; i < n; i ++){
for(int j = 0; j < m; j++){
backtrace(board,word,n,m,i,j,0,visit);
}
}
}8.给定n个工人和n个任务,和cost[n][n]表示第i个工人干第j个任务的开销,使用分支限界法使得开销最少
这题可以使用优先队列的分支限界法,我在做的时候没有给出完整逻辑,大致逻辑如下:
定义一个最小堆min_heap,按照当前已经耗费+剩下工人每个人选剩下的最小耗费来进行比较,第一个完成分配的就是最终的结果。
在遍历时由于是排列,可以采取swap进行遍历,但是我在写的时候由于min_heap里面我设计了最小耗费和当前安排的工作数量,我加上了安排了工人vector<int> people,所以遍历时我使用find查看当前工人是否已经在people中来遍历。
给出伪代码:
cpp
int BFS(int **cost,int n){
min_heap<node> prior_q;
for(int i = 0; i < n; i++){
prior_q.push(node(cost[i][0]+last,1,i));//分别是累计开销,下一个执行任务,当前的工人
}
while(!prior_q.empty()){
curr_node = prior_q.front();
prior_q.pop();
if(curr_node.t == n) return curr_node.cost;
for(int i = 0; i < n; i++){
if(!curr_node.find(i)){
prior_q.push(node(cost[i][t]+last,t+1,i));
}
}
}
}