Hello,大家好,我们又见面了,今天,我来继续给大家介绍算法竞赛进阶内容。上一期我给大家分享了重链剖分,这一期,我来给大家分享树链剖分的另外一种常见形式 --- 长链剖分。
相信这篇博客一定会对大家有所帮助~~~
想要平滑的学习这一期内容,还是希望大家首先去看一下本专辑的上一篇文章《重链剖分》。
那么废话不多说,我们直接开始。
一:引入
长链剖分 vs 重链剖分
重链剖分:根据子树的大小,把树拆分成若干条互不相交的重链;
长链剖分:根据子树的深度(高度),把树拆分成若干条互不相交的长链
二:相关概念
以下是树的长链剖分相关的概念:
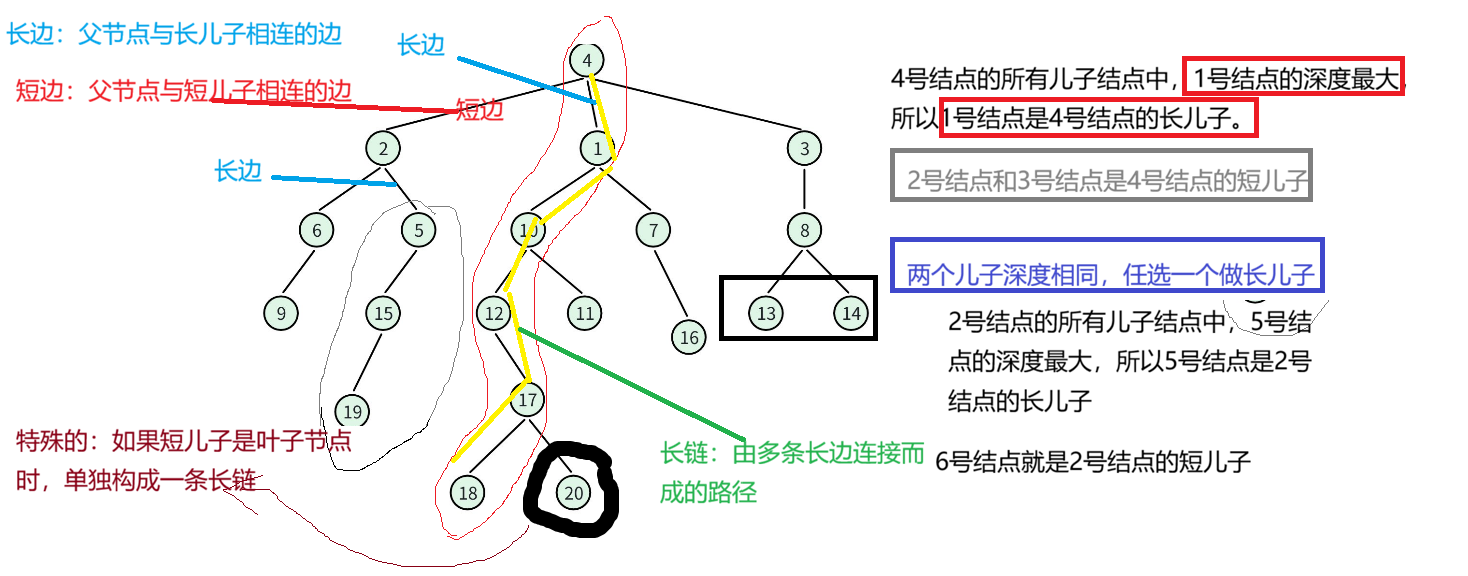
长儿子:父节点的所有儿子中,子树深度最大的结点。
短儿子:父结点中,除了长儿子以外的儿子。
3.长边:父结点与长儿子相连的边。
短边:父结点与短儿子相连的边。
长链:由多条长边连接而成的路径。特殊的,如果短儿子是叶子节点时,单独构成一条长链。
下面通过一张图来理解一下这些概念:
三:长链剖分
将一整棵树分成若干条长链的过程,就叫做长链剖分。
如下图所示:
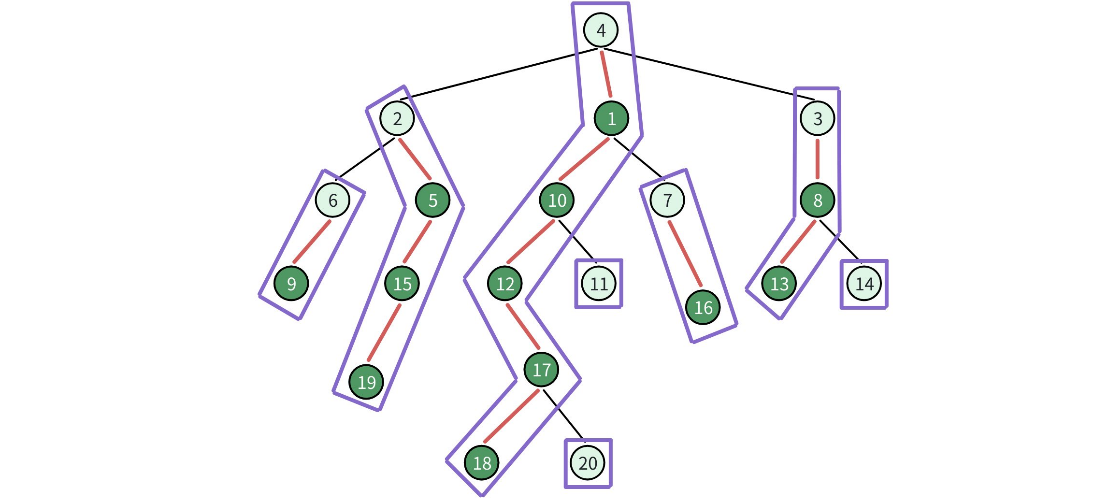
上图就是将一棵树进行长链剖分之后的结果,大家是不是觉点有一点熟悉???没错,上一篇文章中的重链剖分也是这棵树,而且剖分结果是一模一样的。
但是,这并不表明重链剖分和长链剖分的结果是一样的,只是这棵树比较特殊,一般情况下,两者最终的剖分结果其实是不同的。大家可以多画几棵树,就可以发现两者其实是不同的。
四:代码实现
1. 预备工作:
要实现长链剖分,先定义几个数组:
fa[x] 表示:结点 x 的父亲节点;
dep[x] 表示:结点 x 的深度;
3. len[x] 表示:结点 x 走到叶子节点,最多经过的点数;
4. son[x] 表示:结点 x 的长儿子;
5. top[x] 表示:结点 x 所在长链的顶部节点;
- dfn[x] 表示:结点 x 的 dfn 序;
具体代码实现:
两次 dfs 就可以维护出上面所列的信息
2. 第一次 dfs:
第一次 dfs 先维护前四个数组的信息:
cpp
int n;
vector<int> edges[N];
int fa[N], dep[N], len[N], son[N], top[N], dfn[N], idx;
void dfs1(int x, int f)
{
fa[x] = f; dep[x] = dep[f] + 1;
for(auto y : edges[x])
{
if(y == f) continue;
dfs1(y, x);
if(len[y] > len[son[x]]) son[x] = y;
}
len[x] = len[son[x]] + 1;
} 2. 第二次 dfs:
第二次 dfs 维护最后两个数组的信息:
cpp
void dfs2(int x, int t)
{
top[x] = t; dfn[x] = ++idx;
if(son[x]) dfs2(son[x], t);
for(auto y : edges[x])
{
if(y == fa[x] || y == son[x]) continue;
dfs2(y, y);
}
} 五:性质
长链剖分有以下两个性质:
性质一:
任何一个结点 x 的 k 级祖先 y 所在长链的长度一定大于等于 k。
这个结论显然正确,可以通过反证法证明。
1. 如果 y 所在的长链长度小于 k,那么它就不是长链了,显然从 y 走向 x 这条链更优。
2. 于是 y 所在长链的长度一定大于等于 k,性质是成立的。

性质二:
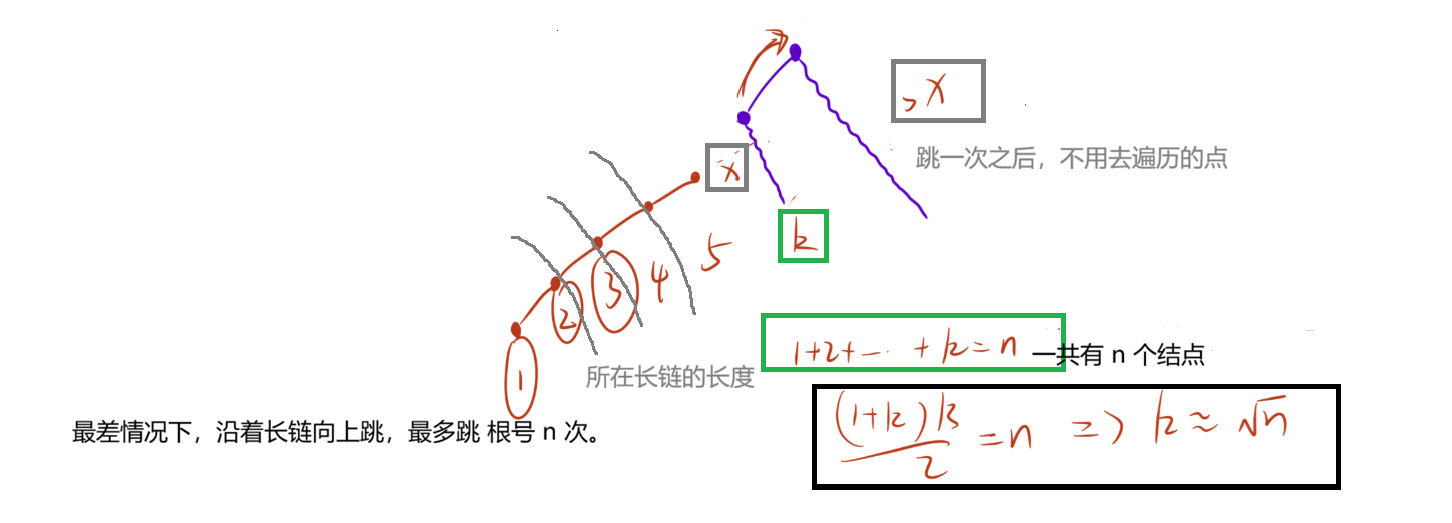
一个结点跳跃长链(沿着长链跳)到根节点,跳跃的次数最多为 O(根号 n)。
证明:
1. 如果一个节点 x 从一条长链跳到了另外一条长链上,那么跳跃到的这一条长链的长度不会小于之前的长链长度。(由性质一得到)
2. 考虑最差的情况,每一次跳跃的链长分别为 1,2,3,4,......k,一共跳 n 个结点,由 n = 1 + 2 + 3 + 4 + ...... +k,可知最多跳根号 n 次。
六:总结
因为长链剖分向上跳的次数比较多,时间复杂度较高,根号 n 级别,我们一般不会使用长链剖分来解决上一篇文章中的路径修改和查询问题。使用长链剖分解的话,不具有优势。
但是,长链剖分有它独特的用武之地,长链剖分和重链剖分是相辅相成的。
我们一般用长链剖分后的特征,来处理一些特定的问题以及优化 dp。
之后,我会给大家介绍长链剖分的应用场景。这一期就先到这里了。
如果大家感觉有所收获的话,别忘了一键三连,我们下一期再见!!!